Элементарные логические операции

1.

Элементарные логические операции

2.

Из
множества
логических
функций
выделяется ряд наиболее простых операций,
которые имеют ясную логическую интерпретацию:
1) отрицание (инверсия)
f 1 x x
Отрицание – это функция,
выражающая
высказывание,
которое
истинно,
если
высказывание ложно, и ложно,
если истинно.
(читается: не).

3.

2) дизъюнкция (логическое сложение)
f 2 x, y x y
(читается: " x или y ").
Дизъюнкция
–
это
функция,
выражающая
высказывание,
которое
истинно тогда и только
тогда, когда, по крайней
мере,
одно
из
высказываний x или y
является истинным.

4.

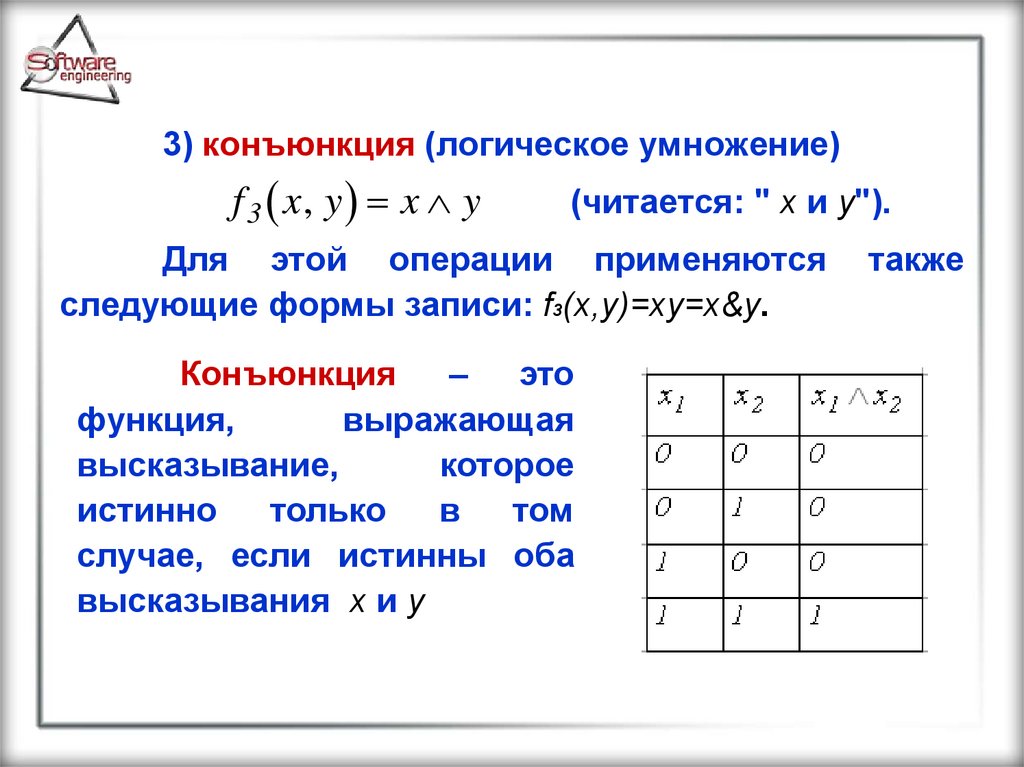
3) конъюнкция (логическое умножение)
f 3 x, y x y
(читается: " x и y").
Для этой операции применяются
следующие формы записи: f3(x,y)=xy=x&y.
Конъюнкция
– это
функция,
выражающая
высказывание,
которое
истинно
только
в
том
случае, если истинны оба
высказывания x и y
также

5.

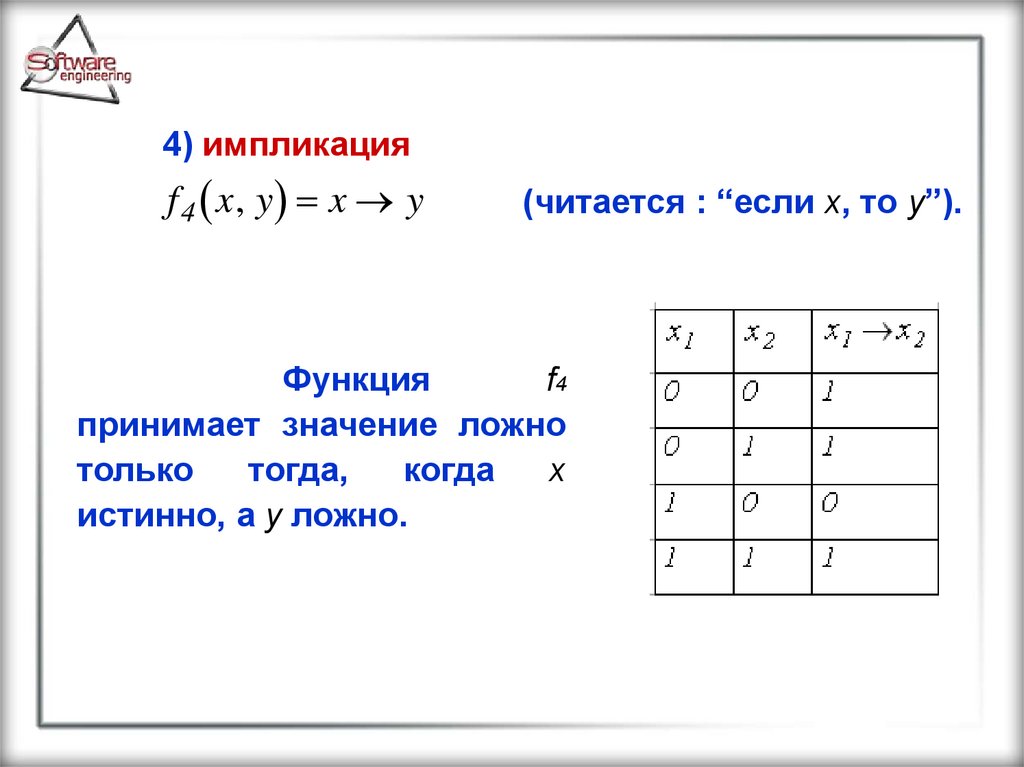
4) импликация
f 4 x, y x y
(читается : “если x, то y”).
Функция
f4
принимает значение ложно
только
тогда,
когда
x
истинно, а y ложно.

6.

5) эквивалентность (равнозначность)
f 5 x, y x ~ y
(читается:
Функция f5=1 тогда и
только тогда, когда значения
обоих аргументов x и y
совпадают
“x равно y ”).

7.

6)
сложение
(неравнозначность)
по
f 6 x, y x y
Функция f6 истинна
тогда и только тогда, когда
значения
аргументов
различны,
функция
является обратной к f5
модулю
два

8.

7) штрих Шеффера
f7 x , y x y
Операция обратная по
отношению к конъюнкции
(функция
ложна,
только
если
оба
аргумента
истинны)

9.

8) стрелка Пирса
f 8 x, y x y
Функция f8 обратная к
дизъюнкции
(f8
истинно,
только когда x и y ложны)

10.

Наиболее важными функциями являются
первые три. Остальные могут быть выражены
через эти три функции. С использованием трех
основных функций (дизъюнкции, конъюнкции и
отрицания) могут образовываться более сложные
функции.
Поэтому можно
дать
еще одно
определение булевой алгебры.
Булевой алгеброй называется алгебра типа,
несущим множеством которой является множество
двоичных чисел, а операциями - конъюнкция,
дизъюнкция и отрицание.

11.

Свойства основных логических функций

12.

Основные
логические
функции
следующими свойствами:
обладают
1) коммутативность: a b b a
a b b a
2) ассоциативность:
a b c a b c
a (b c) (a b) c
3) идемпотентность конъюнкции и дизъюнкции:
a a a
a a a

13.

4) дистрибутивность:
а) конъюнкции относительно дизъюнкции:
a b c a b a c
б) дизъюнкции относительно конъюнкции:
a b c a b a c
5) двойное отрицание:
a a

14.

6) правило де Моргана:
a b a b
a b a b
7) правило склеивания:
a b a b a
(a b) (a b) a
;
8) правило поглощения:
a ab a
a (a b) a
a ab a b
a (a b) a b

15.

9) действия с константами:
a 0 a
a 0 0
a 1 1
a 1 a
a a 1
a a 0
Свойства
основных
булевых
функций
доказываются
либо
путем
преобразования
выражений, либо на основе сопоставления таблиц
истинности правой и левой части равенства.

16.

Пример. Доказать, что
a b a b
С
учетом
таблиц
истинности
элементарных
логических
операций
определяем
последовательно
значения
функций, указанных в верхней строке для всех
возможных значений аргументов
и , т.е.
построим для них соответствующие им
таблицы истинности

17.

a b a b
Так как значения функций a b и a b на всех
наборах совпадают, то эти функции равны.

18.

Задание функции формулой. Эквивалентные
преобразования логических выражений

19.

Понятие
формулы вводится
для
формализации представления и записи простого
или сложного высказывания.
Формула рассматривается как некоторый
способ реализации функции и вводится индуктивно
в соответствии со следующим правилом: если А и
В – высказывания (простые или сложные,
постоянные или переменные), то запись значения
истинности каждого из этих высказываний – есть
формула; если А и В – формулы, то выражения
«А * В» и «Ā» (где символ * обозначает знак одной
из рассмотренных выше элементарных логических
операций) – тоже формулы.

20.

Таким
образом,
рассмотренные
выше
выражения, которыми описывались элементарные
логические операции и свойства основных
логических операций, - суть формулы. Применение
по отношению к ним указанного правила позволяет
получить новые формулы, соответствующие более
сложным высказываниям.
Новые формулы могут быть получены на
основе использования понятия суперпозиции
функций.
Суперпозицией
функций
f1,
f2,
…,
fn
называется
функция
f,
полученная
путем
подстановки функций f1, f2, …, fn друг в друга и
переименования переменных.

21.

Пример. Пусть функция задана формулой
f 0 z1 , z2 z1 z2 , и при этом имеет место
равенство
z1 A1 x1 x2 ,
z 2 A2 x3
Тогда новую формулу E можно получить путем
подстановки A1 и A2 в исходную формулу:
f 0 x1 , x2 , x3 x1 x2 x3

22.

Логические операции обладают различным
приоритетом, с точки зрения порядка выполнения
их в выражении. Принят следующий порядок
выполнения операций в булевой алгебре: в первую
очередь вычисляются выражения, над которыми
стоит знак отрицания, далее выполняются
операции конъюнкции , а затем дизъюнкции .
Если выражение, заключенное в скобках,
представляет конъюнкцию или имеет общий знак
отрицания, то скобки опускаются.

23.

Сопоставляя введенные выше понятия
логической функции и формулы, следует иметь
ввиду, что
логическая функция
- это зависимость
между логическими переменными, однозначно
определяемая таблицей истинности, а
формула
это
выражение,
которое
используется для описания логической функции,
причем одна и та же логическая функция может
описываться несколькими формулами.

24.

Пример. Рассмотрим две формулы:
f x1 , x2 x1 x2
и
f x1 , x2 x1 x2
Несложно показать, что обе формулы
представляют одну и ту же функцию, так как
таблицы истинности у них одинаковы.
Формулы, соответствующие одной и той
же функции, называются эквивалентными или
равносильными.

25.

Две формулы U и B называются эквивалентными
(равносильными), если они реализуют одну и ту же
функцию. При этом записывают: U=B.
Эквивалентные
преобразования
логических
выражений. Эквивалентные преобразования – это такие
преобразования формул, при которых сохраняется их
эквивалентность.
Преобразование
называется
эквивалентным, если исходная формула
U x1 , x2 , ..., xn и
полученная
в
результате
B x1 , x2 , ..., xn принимают
преобразования формула
одинаковые значения на каждом наборе значений
аргументов.

26.

Эквивалентное
преобразование
осуществляется на основе сопоставления
таблиц истинности, либо на основе применения
свойств основных логических операций.
Покажем
примеры
эквивалентных
преобразований, которые позволяют получить
новые формулы для описания функций f4 - f8,
используя только знаки операций конъюнкции,
дизъюнкции и отрицания.

27.

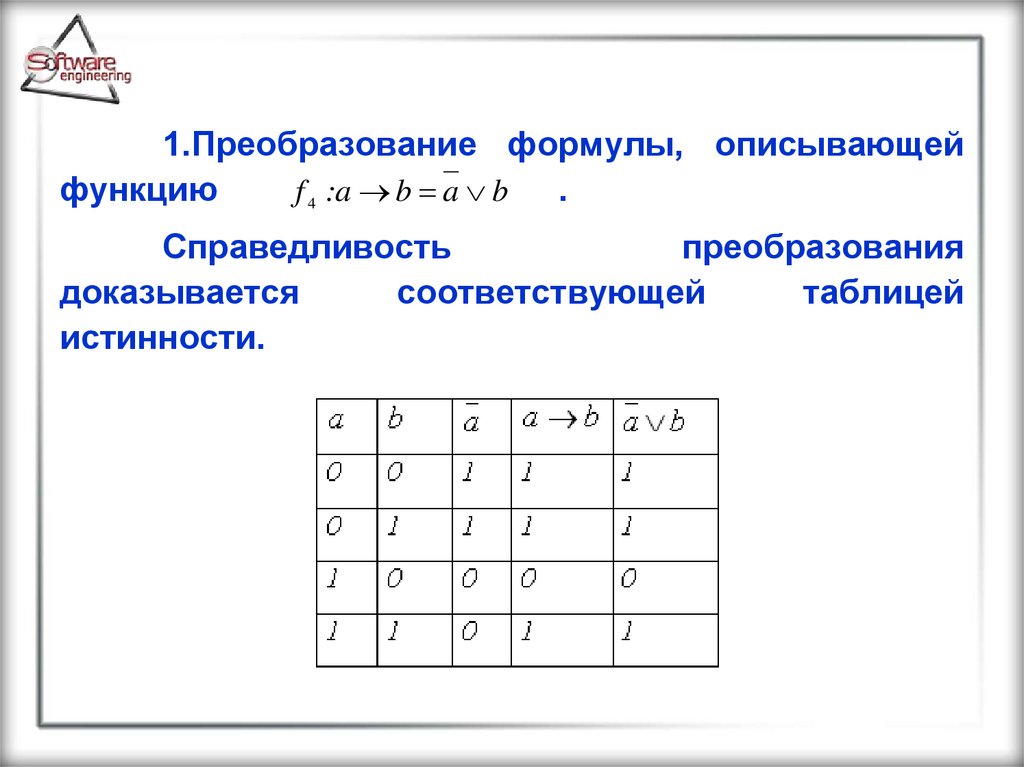
1.Преобразование формулы, описывающей
функцию
.
f 4 :a b a b
Справедливость
преобразования
доказывается
соответствующей
таблицей
истинности.

28.

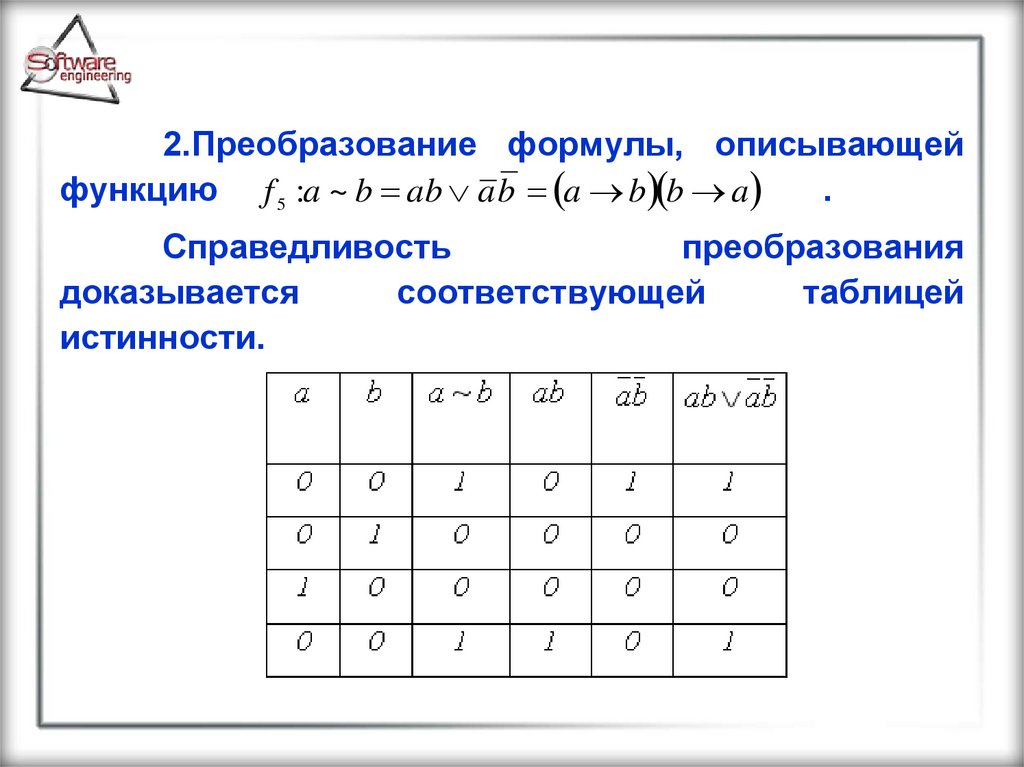
2.Преобразование формулы, описывающей
функцию f 5 :a ~ b ab a b a b b a
.
Справедливость
преобразования
доказывается
соответствующей
таблицей
истинности.

29.

3. Функция f6
a b a ~ b ab a b ab a b (a b) (a b)
4. Функция f7
ab
= a b
5. Функция f8
a b = a b

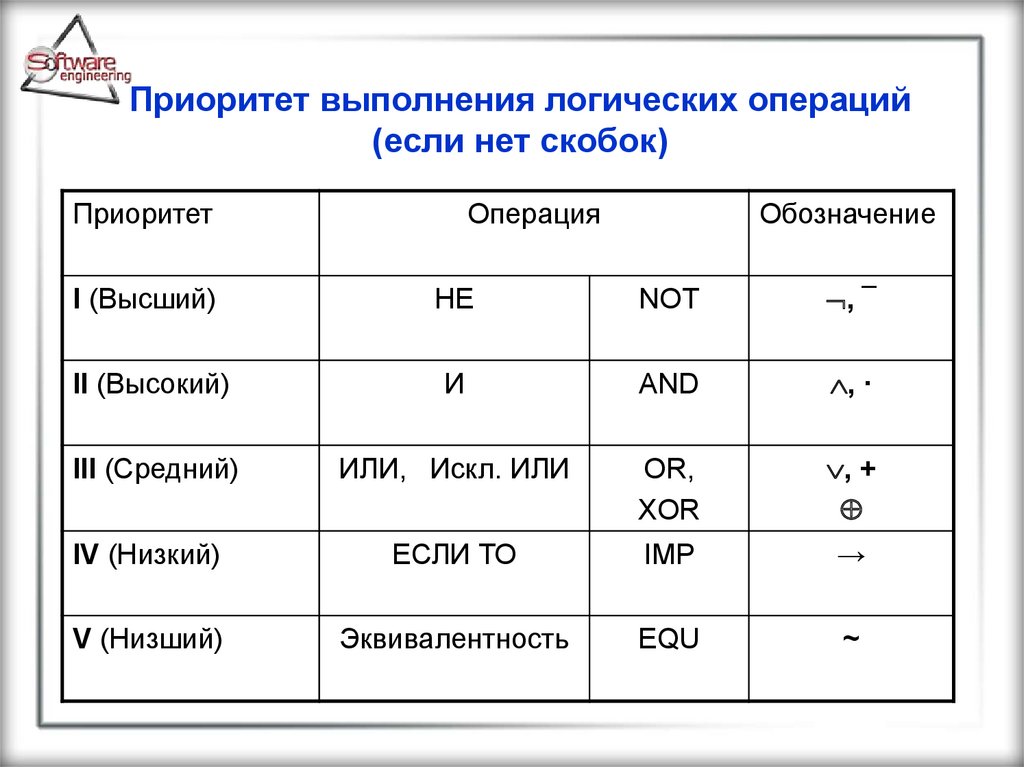
30. Приоритет выполнения логических операций (если нет скобок)

Приоритет
Операция
Обозначение
I (Высший)
НЕ
NOT
, ¯
II (Высокий)
И
AND
, ·
III (Средний)
ИЛИ, Искл. ИЛИ
OR,
XOR
, +
IV (Низкий)
ЕСЛИ ТО
IMP
→
V (Низший)
Эквивалентность
EQU
~

31.

Формулы, из которых построена некоторая
исходная формула, называются подформулами.
Чаще всего эквивалентные преобразования
основаны на замене подформул на эквивалентные
им подформулы.
Если в формуле U заменить подформулу B
на эквивалентную ей под формулу B’, то формула
перейдет U в эквивалентную ей формулу U’.

32.

Упростить выражения:
1
2
3
4
5
6
7
8
9
10
( P ( P Q)) Q

33.

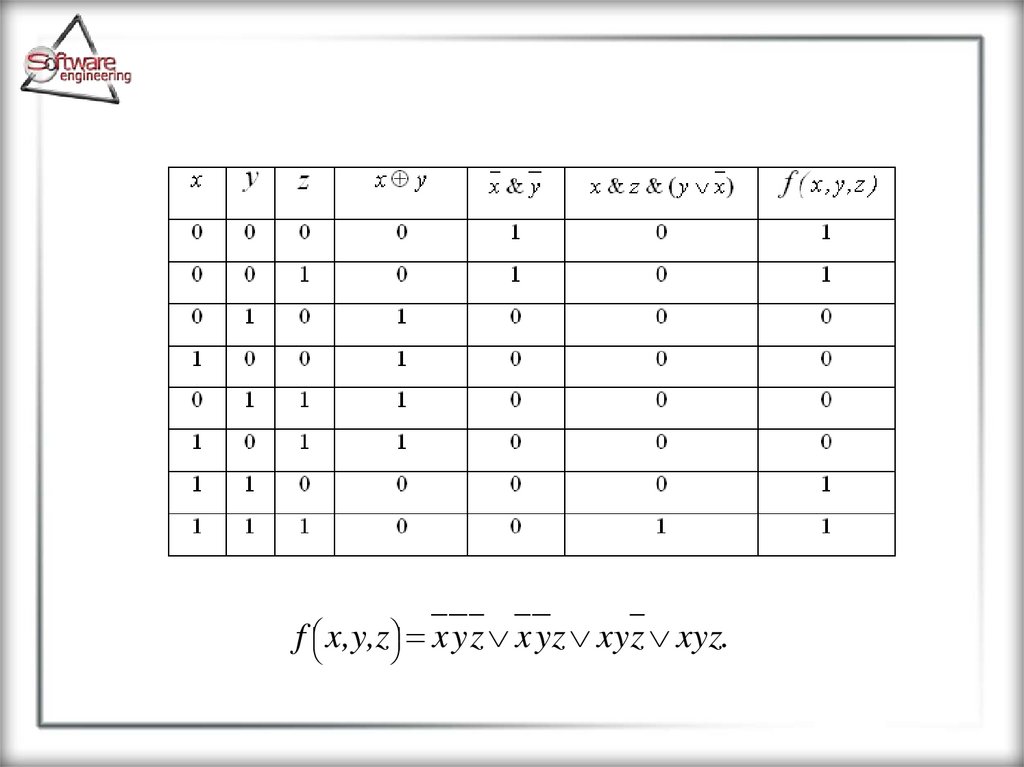
Пример. Рассмотрим пример приведения
заданной логической функции к форме СДНФ, с
использованием обоих известных способов.
f ( x, y, z ) ( x y ) y & x x & z & ( y x ) ( x y ) & ( x y )
x& y x& y&z x&z&x x y x y x& y x& y&z
x& y x& y x& y x& y&z x& y x& y x& y&z
x & y &( z z ) x & y &( z z ) x & y & z x & y & z x & y & z
x& y&z x& y&z x& y&z x& y&z x& y&z
x&y&z x&y&z

34.

f x,y,z x y z x yz xy z xyz.

35.

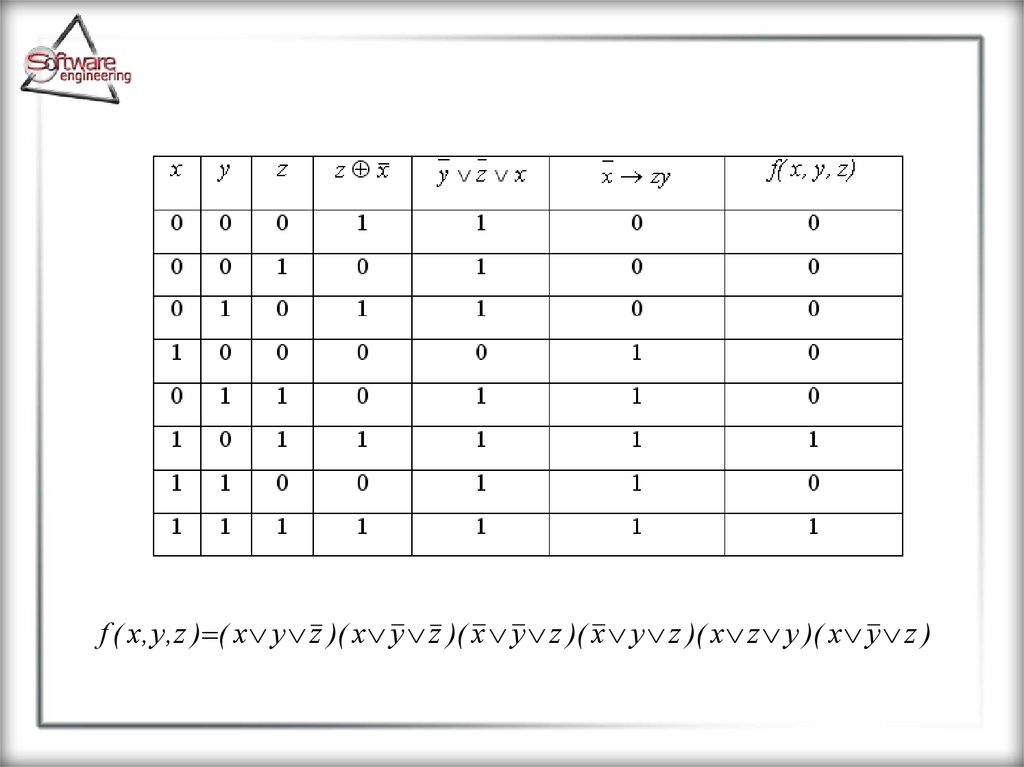
Пример. Рассмотрим пример приведения
заданной логической функции к форме СКНФ, с
использованием обоих известных способов.
f ( x, y, z ) ( z x)( y z x)( x zy ) ( z x )( z x )( x y z )( x zy )
( z x )( z x)( x y z )( x z )( x y ) ( z x yy )( z x yy )( x y z ) &
& ( x z yy )( x y zz ) ( z x y )( z x y )( z x y )( z x y )( x y z ) &
& ( x z y )( x z y )( x y z )( x y z ) ( x y z )( x y z )( x y z ) &
& ( x y z )( x z y )( x y z ).

36.

f ( x, y ,z ) ( x y z )( x y z )( x y z )( x y z )( x z y )( x y z )