Similar presentations:
Графическое отображение технических форм
1.
Лекция 1Графическое отображение
технических форм
2.
Цель:Изучение способа графической
передачи технической
информации.
Задачи: - Изучить метод образования
изображений в технике.
- Овладеть приемами получения
обратимых изображений чертежей.
3.
Объекты отображения и основноесодержание графической
информации
4.
zA
0
x
y
Рис. 1.1
5.
zB
A
0
x
y
Рис.1.2
6.
BA
z
C
D
0
x
y
Рис.1.3
7.
BC
A
z
D
F
K
E
x
L
0
y
Рис.1.4
8.
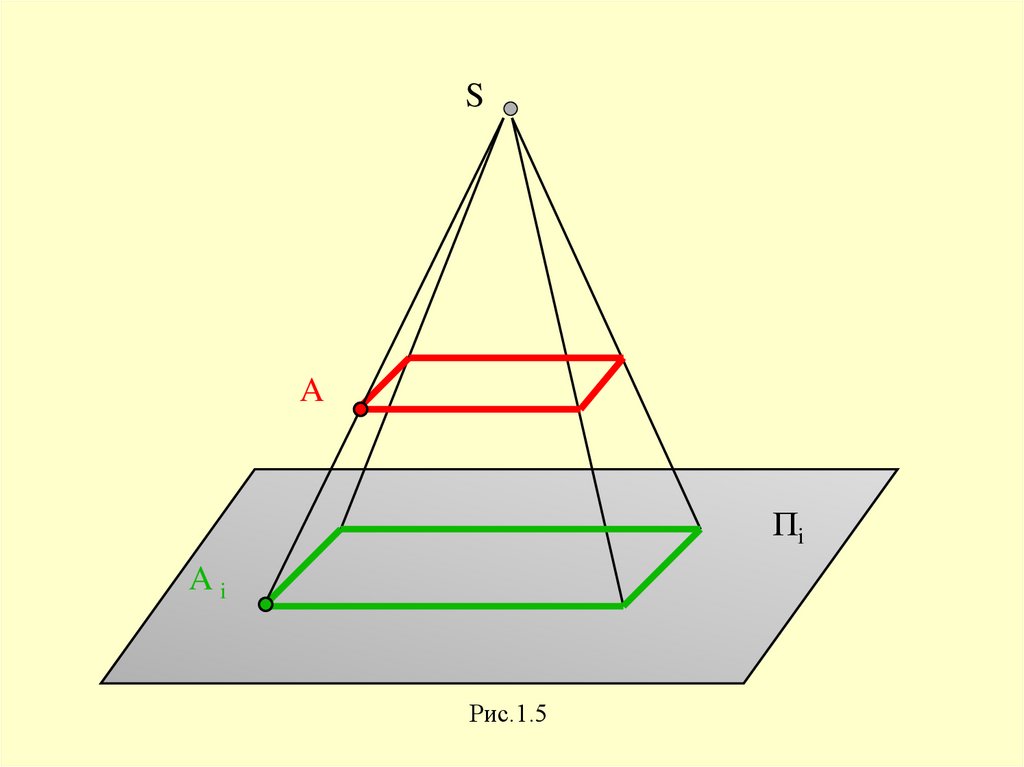
Метод проекций.Аппарат проецирования
9.
Проецирование - это построениеизображения объекта на плоскости
при помощи проецирующих
лучей, исходящих из одной точки (центра)
10.
Полученное изображение - проекция.Плоскость,на которую падают
проецирующие лучи плоскость проекций.
11.
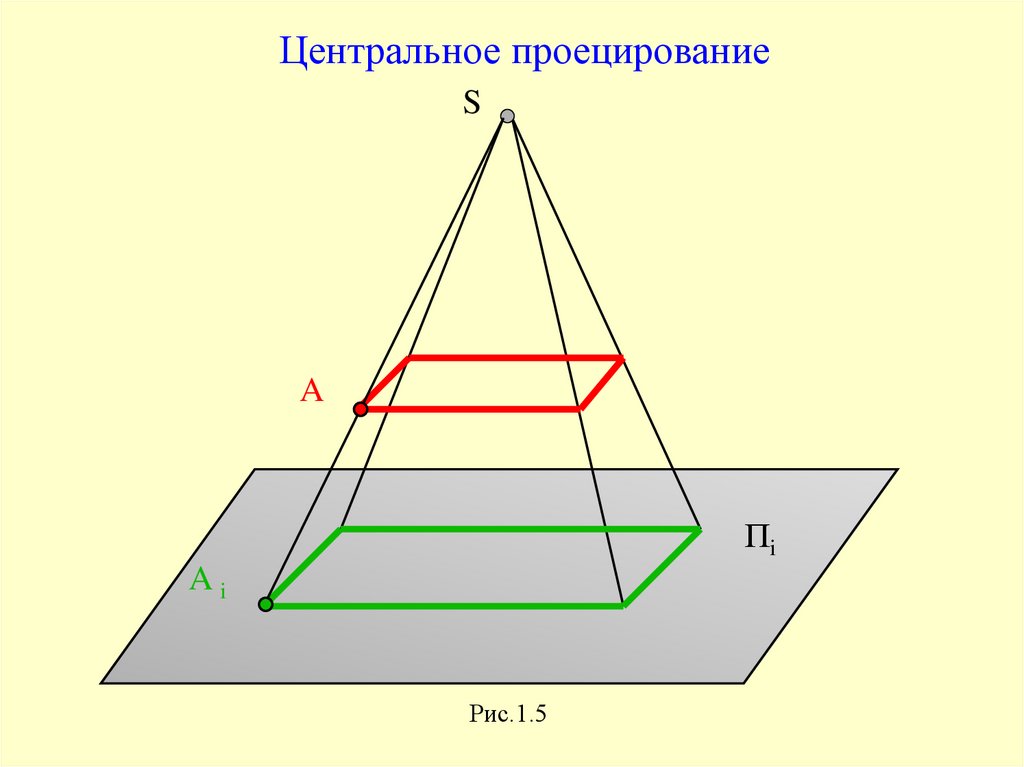
SA
Пi
Ai
Рис.1.5
12.
Аппарат проецирования включает в себя:Пi - плоскость проекций,
S - центр проецирования,
А - объект проецирования (точка),
SA - проецирующую прямую,
Ai - проекцию точки А.
13.
Виды проецирования14.
Центральное проецированиеS
A
Пi
Ai
Рис.1.5
15.
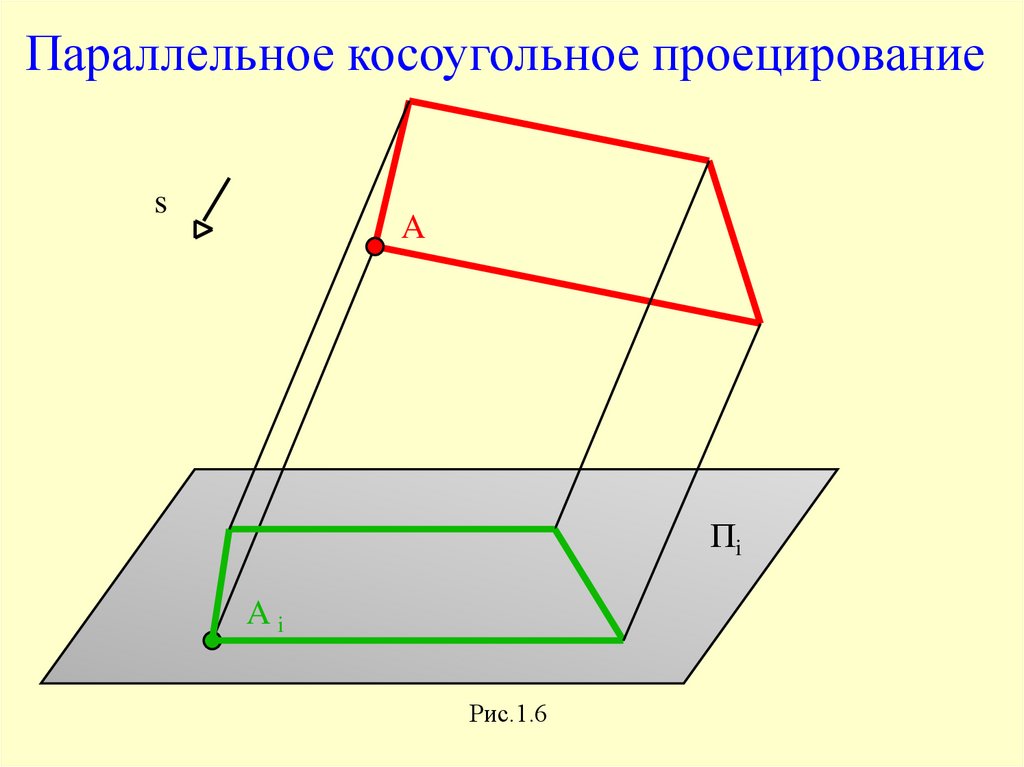
Параллельное косоугольное проецированиеs
A
Пi
Ai
Рис.1.6
16.
Параллельное прямоугольное проецированиеS
A
Ai
Пi
Рис.1.7
17.
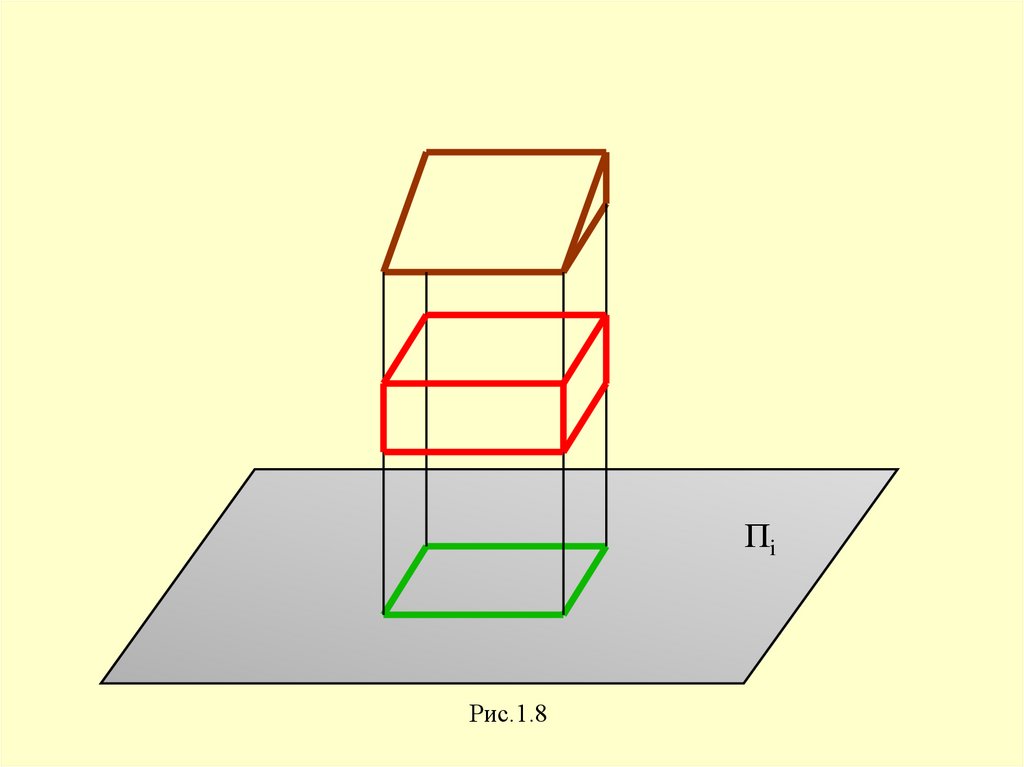
Обратимость изображенийобъектов пространства
18.
ПiРис.1.8
19.
AA
Ai
Рис.1.9
Пi
20.
Обратимость изображений подразумевает возможность однозначного представления формы, размерови
расположения
предмета
в
пространстве
21.
Образование чертежа точки всистеме двух плоскостей проекций
22.
A s`┴ П1A2
А1=s` П1
A s``┴ П2
A2= s`` П2
П2
z
s``
A
II
х
III
I
Ax
s`
O
A1
IV
П1
y
Рис.1.10
23.
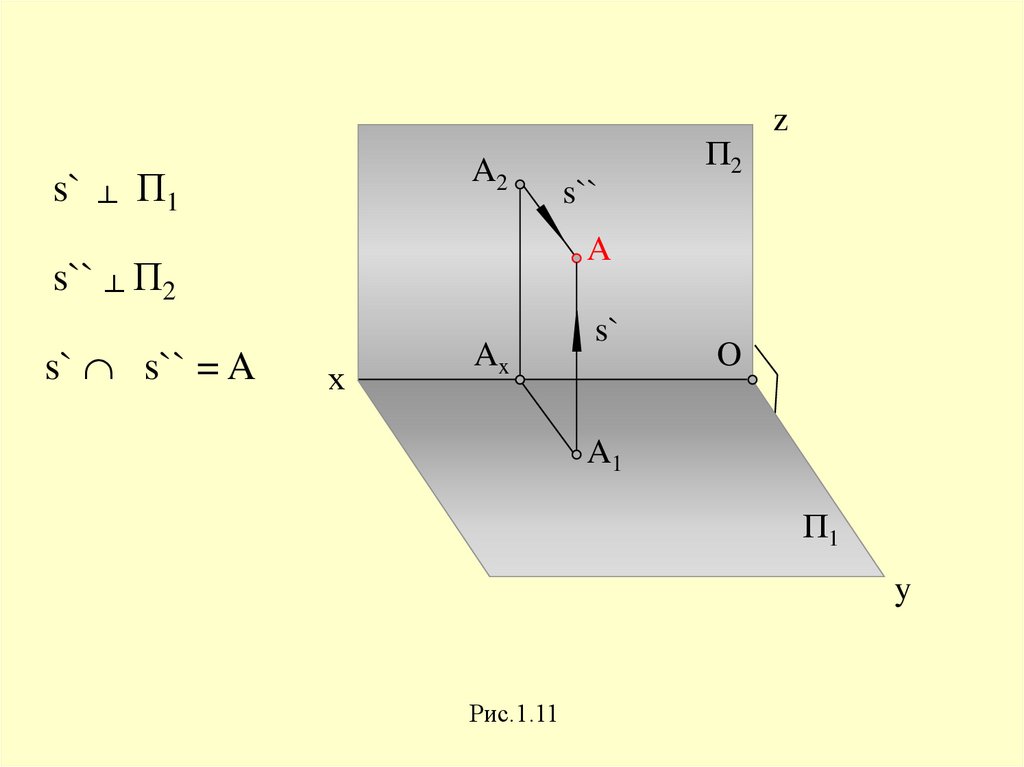
s`┴
A2
П1
s``
A
s`` ┴ П2
s` s`` = A
П2
z
х
I
Ax
s`
O
A1
П1
y
Рис.1.11
24.
Две проекции точки вполнеопределяют ее положение в
пространстве
относительно
данной
системы
плоскостей
проекций
25.
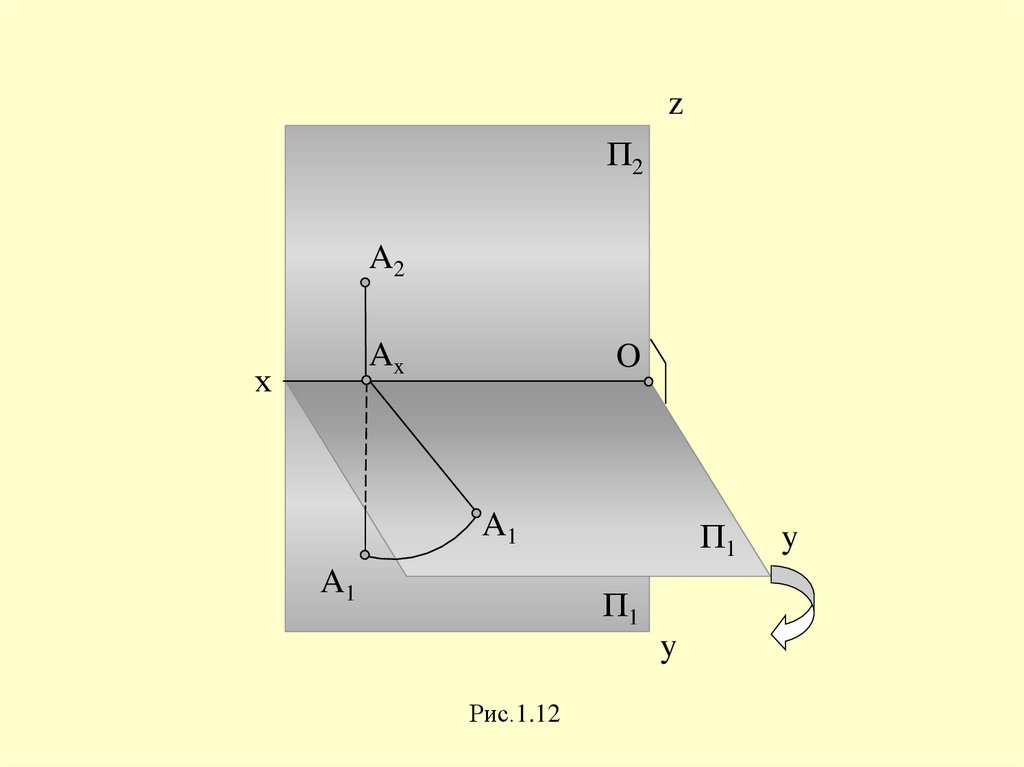
zП2
A2
х
I Ax
O
A1
A1
П1
П1
y
Рис.1.12
y
26.
Врезультате
указанного
совмещения плоскостей П2 и П1
получается чертеж, известный под
названием
эпюр
Монжа
или
двухкартинный чертеж, включающий
две взаимосвязанные проекции “картины”
27.
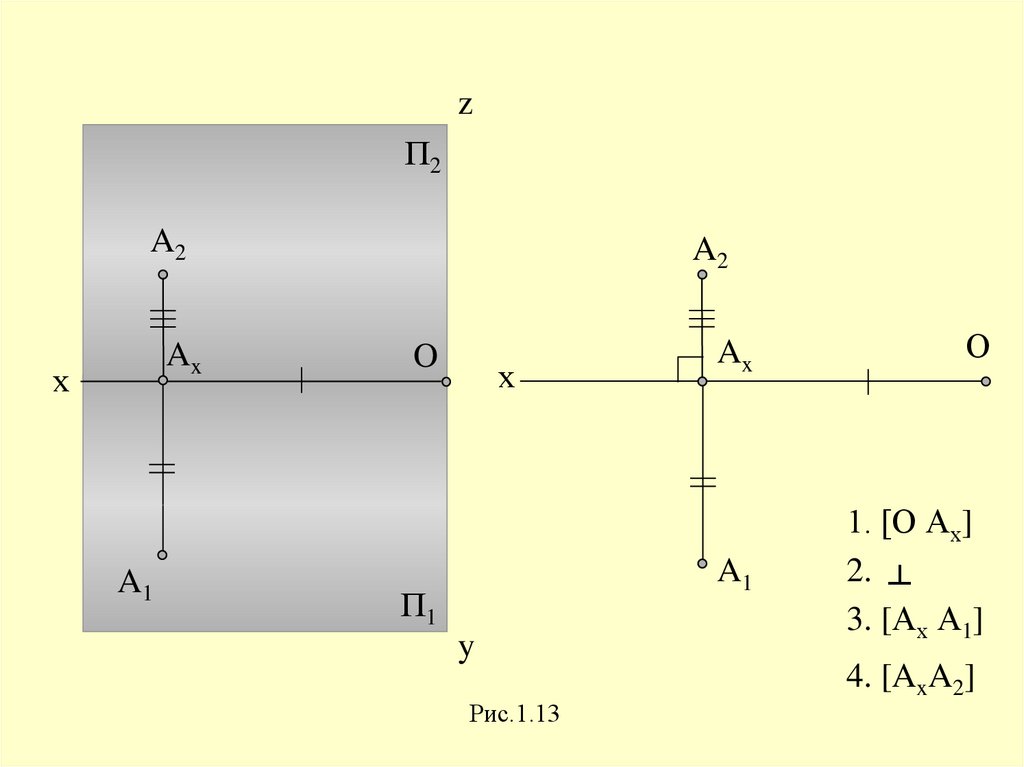
zП2
A2
х
I Ax
A1
A2
O
х
П1
y
Рис.1.13
Ax
О
A1
1. [О Ах]
2. ┴
3. [Ах А1]
4. [AxA2]
28.
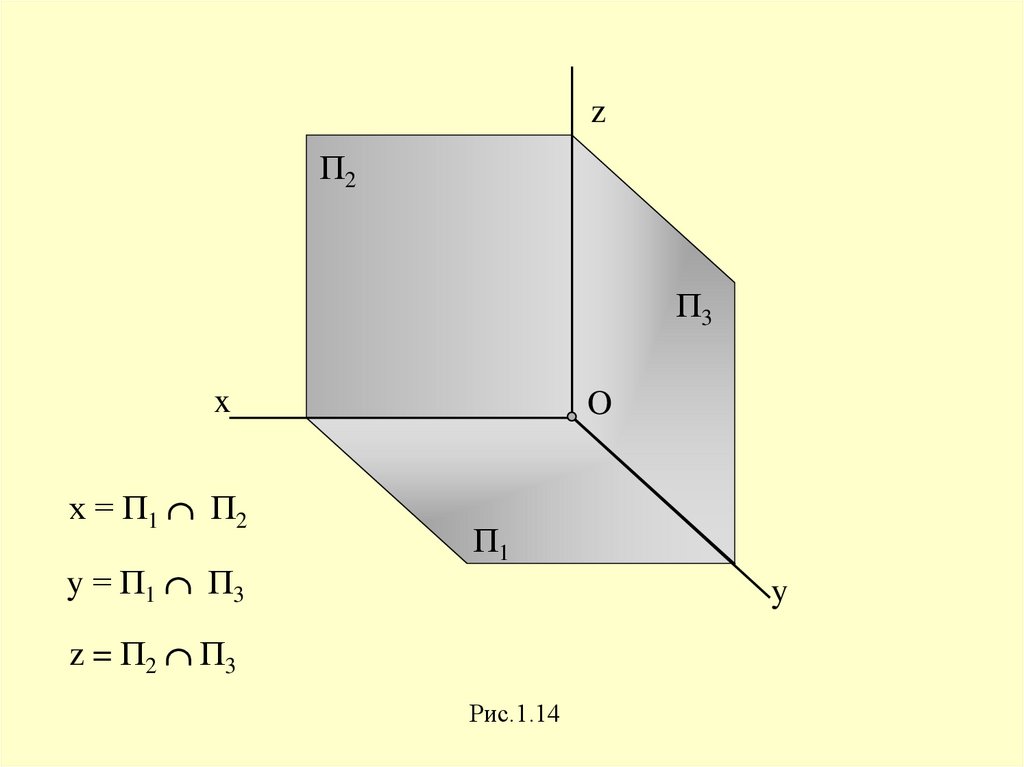
zП2
П3
x
х = П1 П2
y = П1 П3
O
П1
y
z = П2 П3
Рис.1.14
29.
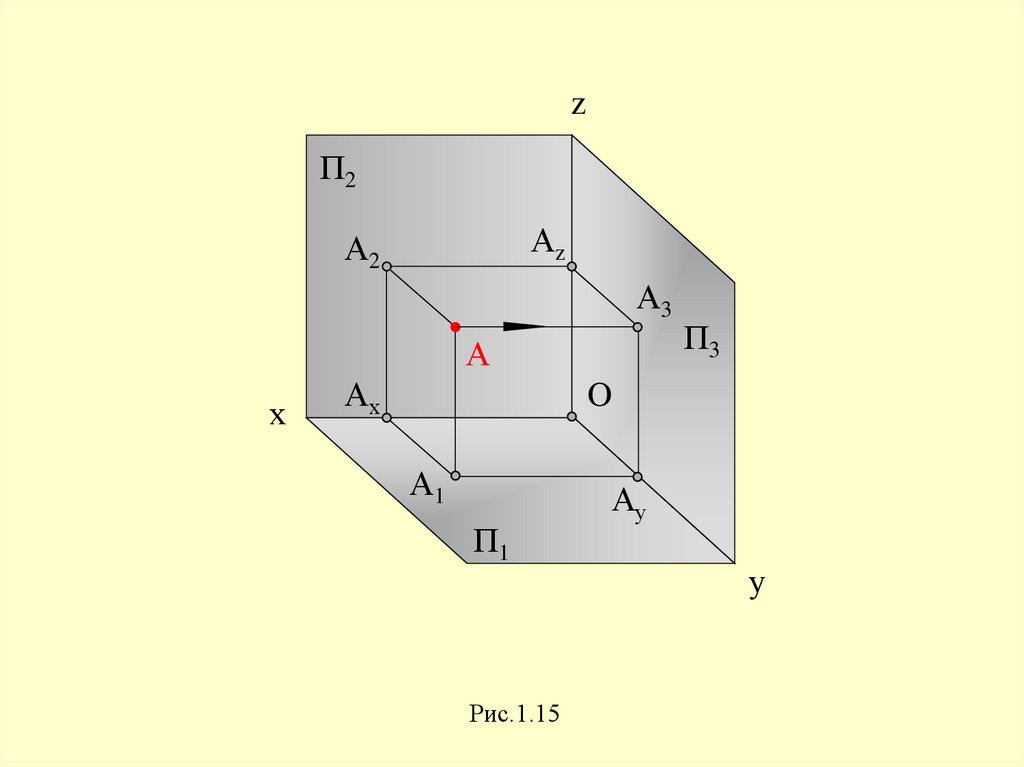
zП2
Аz
А2
А3
А
х
Ах
П3
O
А1
П1
Рис.1.15
Ау
у
30.
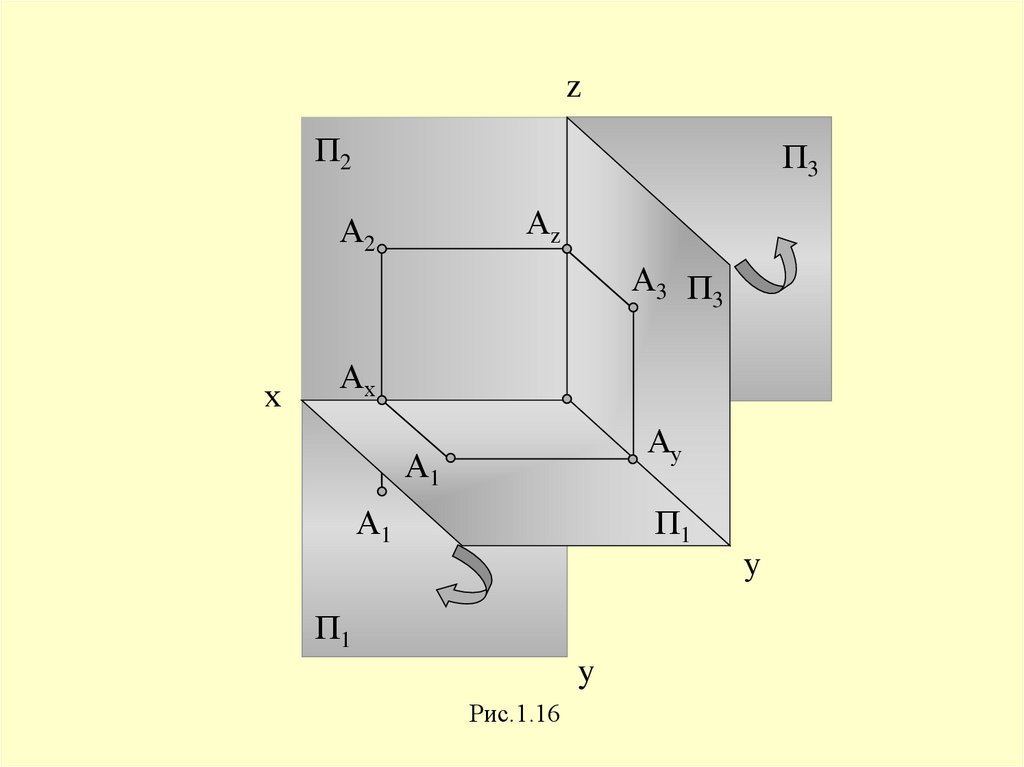
zП2
П3
А3
Аz
А2
А3 П3
х
Ах
O
Ау
А1
А1
П1
П1
П1
y
Рис.1.16
у
31.
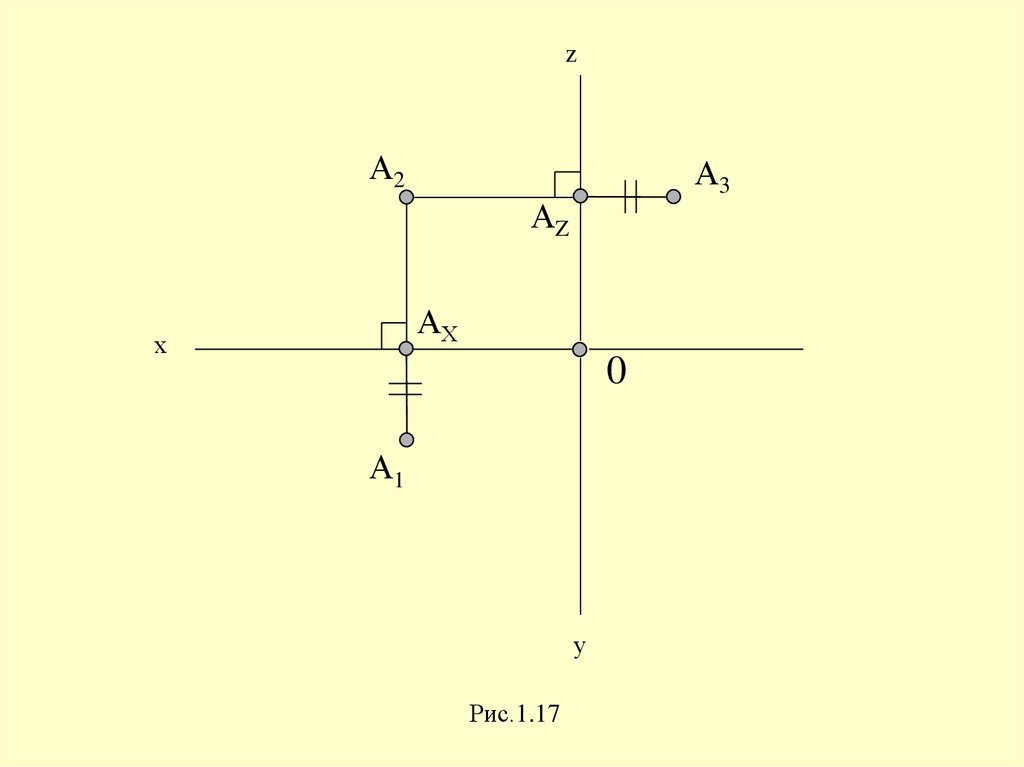
zА2
А3
АZ
АХ
х
0
А1
у
Рис.1.17
32. Выводы:
— Каждая точка пространства характеризуетсятремя координатами: А (х, у, z).
— Каждая проекция точки на чертеже – двумя
координатами: А1 (х, у); А2 (х, z); А3 (у, z).
— Две проекции точки однозначно определяют
ее положение в пространстве.
33.
Образованиеаксонометрического чертежа точки
34.
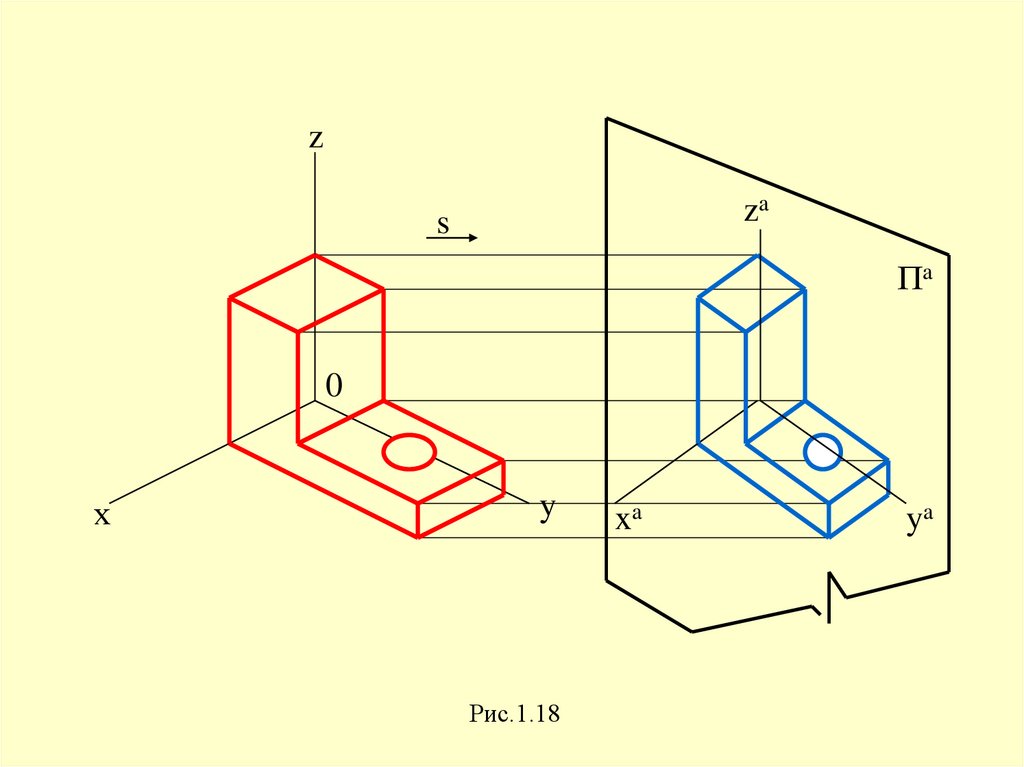
Однокартинный чертеж, обладающийсвойствами наглядности и обратимости,
называется аксонометрическим
35.
zza
s
Пa
0
х
y
Рис.1.18
xa
ya
36.
xyzПa
- натуральная система координат
- аксонометрическая плоскость проекций
xa ya za - аксонометрическая система координат
s
- направление проецирования
37.
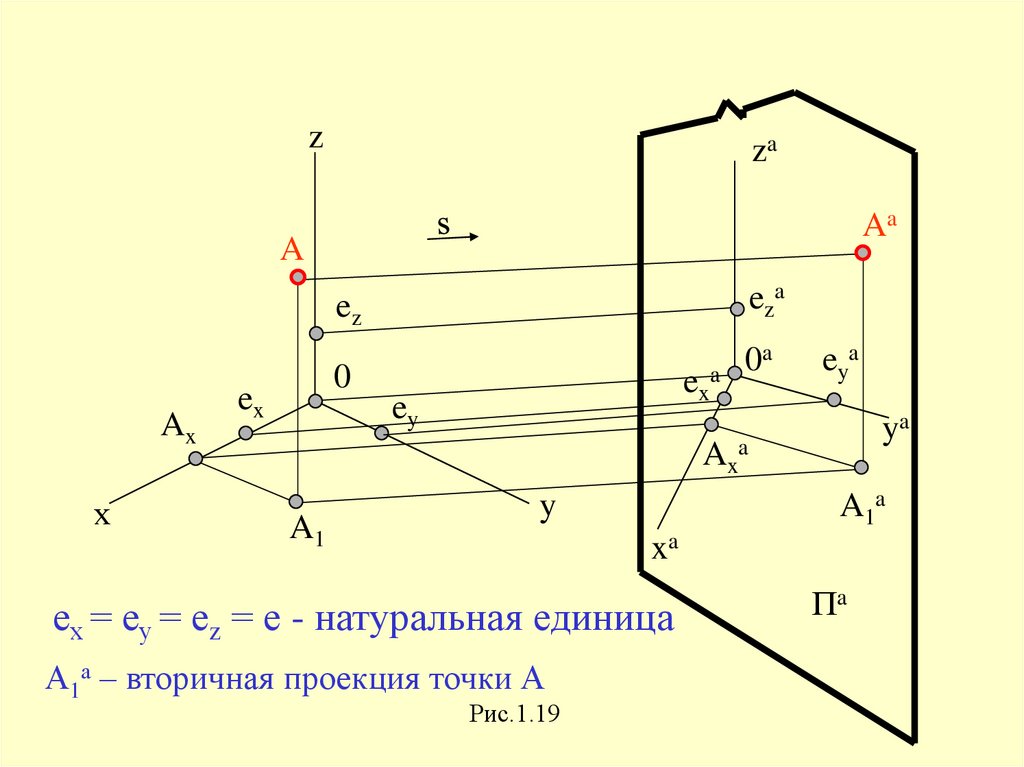
zza
Aa
A
eza
ez
Ax
х
0
ex
ex a
ey
0a
eya
ya
Axa
A1
A1a
y
xa
ех = еу = еz = е - натуральная единица
А1а – вторичная проекция точки А
Рис.1.19
Пa
38.
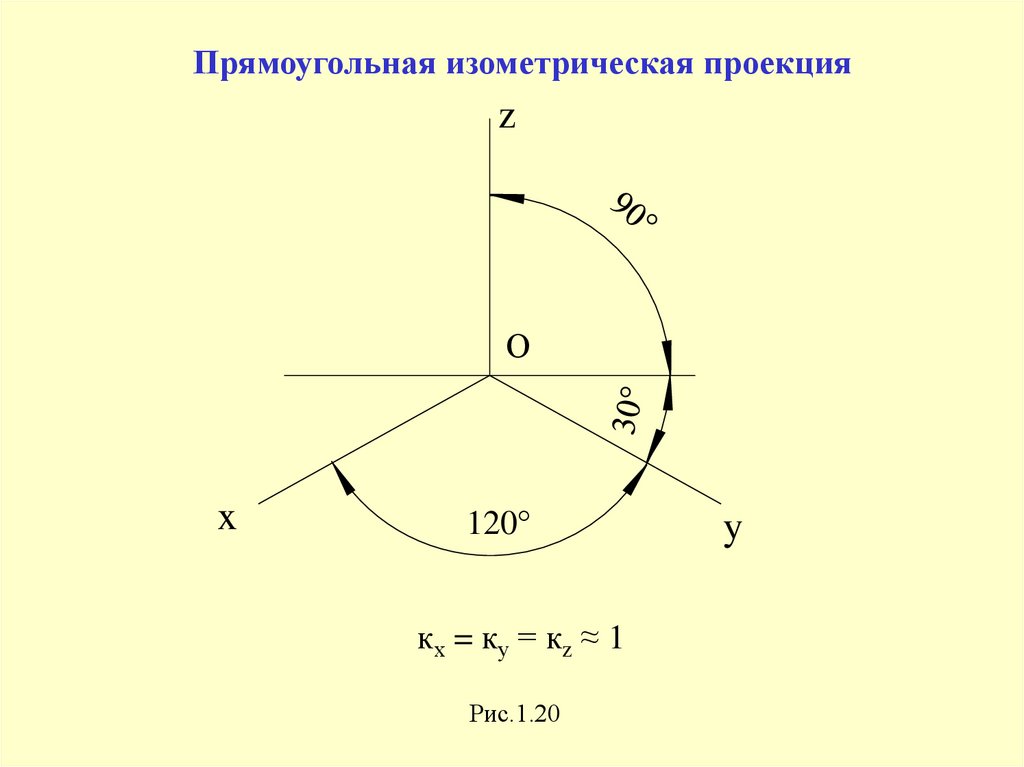
Прямоугольная изометрическая проекцияz
О
x
120°
кх = ку = кz ≈ 1
Рис.1.20
y
39.
Прямоугольная диметрическая проекцияz
7°10'
0
х
41°25'
у
кх = кz ≈ 1;
ky ≈ 0,5
Рис.1.21
40.
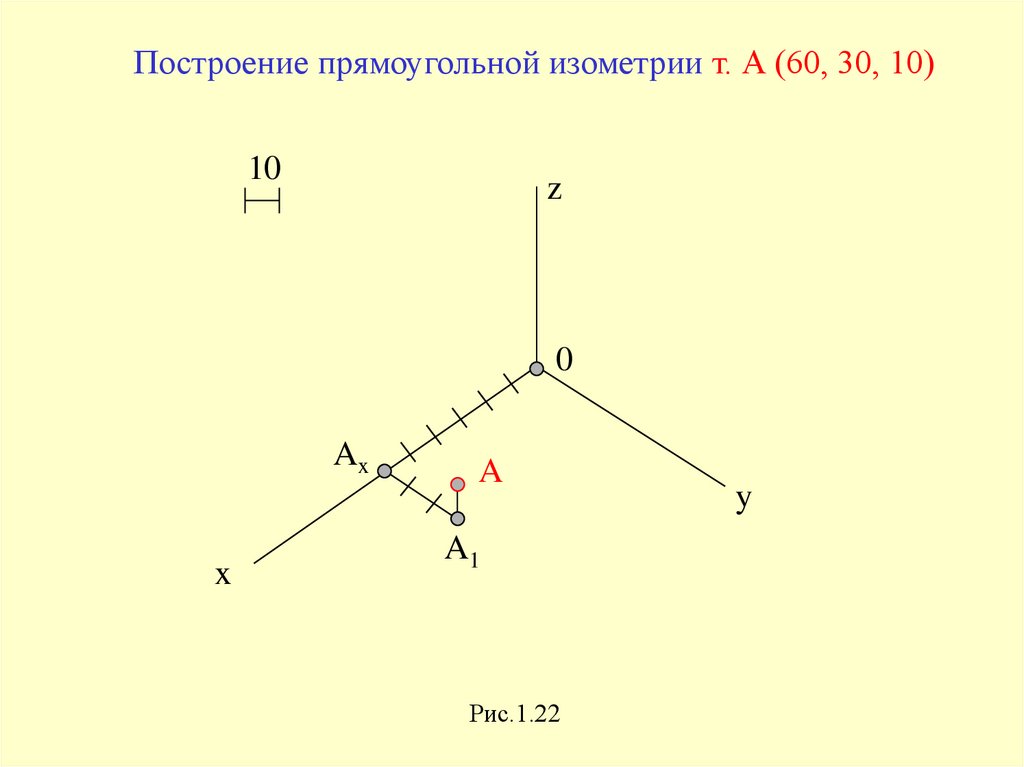
Построение прямоугольной изометрии т. А (60, 30, 10)10
z
0
Ax
x
A
A1
Рис.1.22
y
41.
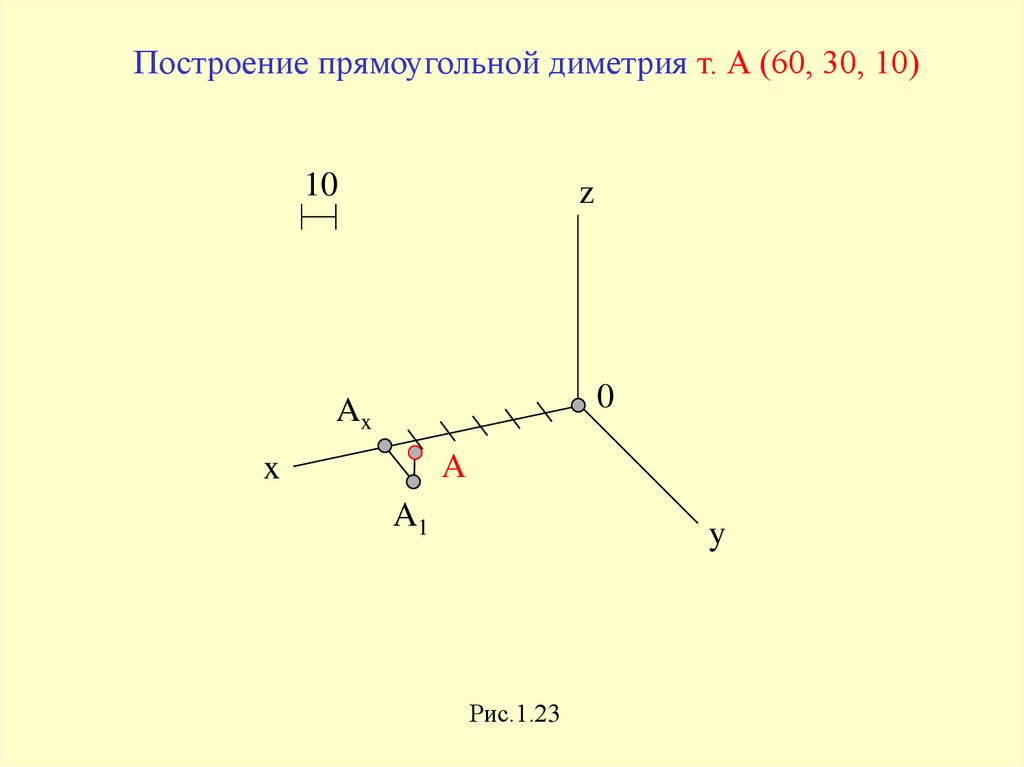
Построение прямоугольной диметрия т. А (60, 30, 10)10
z
0
Ax
A
x
A1
y
Рис.1.23






















 drafting
drafting








