Формулы сокращённого умножения

1.

2.

№ 28.20(а,б) Выполните действия, используя соответствующую формулу сокращённого
умножения:
а) (а – b)(a + b) = a2 – b2
(I – II)(I + II) = I2 – II2
б) (с – d)(c + d) = c2 – d2

3.

№ 28.21(а,б) Выполните действия, используя соответствующую формулу сокращённого
умножения:
а) (х – 1)(х + 1) = х2 – 12 = х2 – 1
(I – II)(I + II) = I2 – II2
б) (9 – а)(9 + а) = 92 – а2 = 81 – а2

4.

№ 28.22(а,б) Выполните действия, используя соответствующую формулу сокращённого
умножения:
а) (3b – 1)(3b + 1) = (3b)2 – 12 = 9b2 – 1
(I – II)(I + II) = I2 – II2
б) (6х – 2)(6х + 2) = (6х)2 – 22 = 36х2 – 4

5.

№ 28.23(а,б) Выполните действия, используя соответствующую формулу сокращённого
умножения:
а) (4а – b)(b + 4а) = (4а – b)(4а + b) =
(I – II)(I + II) = I2 – II2
= (4a)2 – b2 = 16a2 – b2
б) (х + 7)(7 – х) = (7 + х)(7 – х) = 72 – х2 =
= 49 – х2

6.

№ 28.24(а,б) Выполните действия, используя соответствующую формулу сокращённого
умножения:
а) (3х – 5у)(3х + 5у) = (3х)2 – (5у)2 = 9х2 – 25у2
(I – II)(I + II) = I2 – II2
б) (7а – 8b)(7а + 8b) = (7a)2 – (8b)2 =
= 49a2 – 64b2

7.

№ 28.25(а,б) Выполните действия, используя соответствующую формулу сокращённого
умножения:
а) (5х – 2у2)(5х + 2у2) = (5х)2 – (2у2)2 =
(I – II)(I + II) = I2 – II2
= 25х2 – 4у4
б) (2с – 3а2)(3а2 + 2с) = (2с – 3а2)(2с + 3а2) =
= (2с)2 – (3а2)2 = 4с2 – 9а4

8.

№ 28.26(а,б) Выполните действия, используя соответствующую формулу сокращённого
умножения:
а) (4х2 – 2у2)(4х2 + 2у2) = (4х2)2 – (2у2)2 =
(I – II)(I + II) = I2 – II2
= 16х4 – 4у4
б) (10а3 + 5b2)(10а3 – 5b2) =
= (10а3)2 – (5b2)2 = 100а6 – 25b4

9.

№ 28.27(а,б) Используя формулу (а + b)(а – b) = а2 –
– b2, вычислите:
а) 69 · 71 = (70 – 1) · (70 + 1) = 702 – 12 =
(I – II)(I + II) = I2 – II2
= 4900 – 1 = 4899
б) 31 · 29 = (30 + 1) · (30 – 1) = 302 – 12 =
= 900 – 1 = 899

10.

№ 28.28(а,б) Используя формулу (а + b)(а – b) = а2 –
– b2, вычислите:
а) 58 · 62 =(60 – 2) · (60 + 2) = 602 – 22 =
(I – II)(I + II) = I2 – II2
= 3600 – 4 = 3596
б) 82 · 78 = (80 + 2) · (80 – 2) = 802 – 22 =
= 6400 – 4 = 6396

11.

05.09.2020
К л а с с н а я р а б о т а.
Формулы сокращённого
умножения (ФСУ).

12.

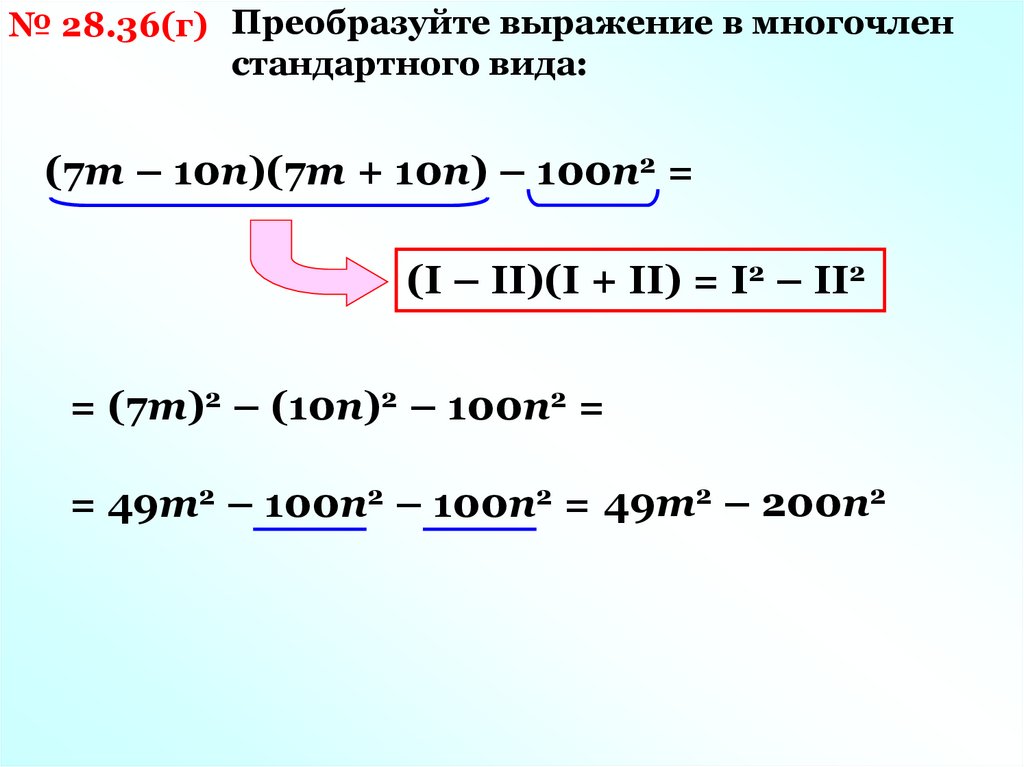
№ 28.36(г) Преобразуйте выражение в многочлен
стандартного вида:
(7m – 10n)(7m + 10n) – 100n2 =
(I – II)(I + II) = I2 – II2
= (7m)2 – (10n)2 – 100n2 =
= 49m2 – 100n2 – 100n2 = 49m2 – 200n2

13.

№ 28.37(в,г) Преобразуйте выражение в многочлен
стандартного вида:
в) 5с(с + 3)(с – 3) = 5с(с2 – 9) = 5с3 – 45с
(I + II)(I – II) = I2 – II2
г) 7d2(d – 1)(d + 1) = 7d2(d2 – 1) = 7d4 – 7d2

14.

№ 28.38(в,г) Преобразуйте выражение в многочлен
стандартного вида:
в) (3b – 1)(3b + 1) – (b – 5)(b + 5) =
(I – II)(I + II) = I2 – II2
= (9b2 – 1) – (b2 – 25) = 9b2 – 1 – b2 + 25 =
= 8b2 + 24

15.

№ 28.38(в,г) Преобразуйте выражение в многочлен
стандартного вида:
(I + II)2 = I2+ 2·I·II + II2
г) (m + 3n)2 + (m + 3n)(m – 3n) =
(I + II)(I – II) = I2 – II2
= (m2 + 9n2 + 6mn) + (m2 – 9n2) =
= m2 + 9n2 + 6mn + m2 – 9n2 = 2m2 + 6mn

16.

№ 28.39(в,г) Преобразуйте выражение в многочлен
стандартного вида:
в) (а – 2)(а + 2)(а2 + 4) = (а2 – 4)(а2 + 4) =
= а4 – 16
г) (с2 – 1)(с2 + 1)(с4 + 1) = (с4 – 1)(с4 + 1) =
= с8 – 1

17.

№ 28.43(в) Решите уравнение:
(6х – 1)(6х + 1) – 4х(9х + 2) = – 1
36х2 – 1 – 36х2 – 8х = – 1
– 8х = – 1 + 1
– 8х = 0 : (– 8)
х=0
Ответ: 0

18.

№ 28.44(в) Решите уравнение:
х(х – 1) – (х – 5)2 = 2
х2 – х – (х2 + 25 – 10х) = 2
х2 – х – х2 – 25 + 10х = 2
– х + 10х = 2 + 25
9х = 27
х=3
Ответ: 3

19.

№ 28.45(в) Решите уравнение:
(2х – 3)2 – 2х(4 + 2х) = 11
4х2 + 9 – 12х – 8х – 4х2 = 11
– 12х – 8х = 11 – 9
– 20х = 2
– 20 – 20
х = – 0,1
Ответ: – 0,1

20.

№ 28.61(б) Замените символы * одночленами так,
чтобы выполнялось равенство:
( I + II )( I – II ) = I2 – II2
( * + * )( * – 11c) = 81a2 – *
(9а + 11с)(9а – 11с) = 81а2 – 121с2

21.

У: стр. 113 § 28
З: § 28 № 36 – 39(а,б).