Свойства вероятности

1.

Вероятность суммы двух
несовместных событий А и В
равна сумме вероятностей
этих событий
Р(А+В)=Р(А)+Р(В)
События называются несовместными, если они
не могут произойти одновременно

2.

Вероятность произведения двух
независимых событий равно
произведению их вероятностей
Р(АВ)=Р(А)Р(В)
События называются независимыми, если
наступление одного из них не влияет на
возможность наступления другого.

3.

Вероятность обратного события
равна
P( A) 1 P( A)

4.

Студент сдает в сессию три экзамена.
Вероятность воспользоваться шпаргалкой
на первом, втором и третьем
экзамене равна соответственно,
0.4, 0.5, 0.7. Найти вероятность того,
что на всех экзаменах студенту
удастся списать.

5.

Пусть событие А1 состоит в том, что студенту
удалось списать на первом экзамене,
А2 - на втором экзамене,
А3 - на третьем экзамене.
Эти события будут независимыми. Событие А,
состоящее в том, что студент спишет на всех трех
экзаменах, выразится как произведение событий
А1 , А2 и А3 :
А=А1А2А3

6.

Тогда по теореме об умножении вероятностей
Р(А)=Р(А1)Р(А2)Р(А3)
Где Р(А1)=0.4
Р(А2)=0.5
Р(А3)=0.7
Следовательно
Р(А)=0.4*0.5*0.7=0.14

7.

Три стрелка стреляют по мишени.
Вероятности попадания в цель
для первого, второго и третьего
стрелков равны 0,9; 0,8 и 0,7. Найти
вероятности событий:
А – все стрелки попали

8.

Пусть событие А1 состоит в том, что попал 1-й
стрелок,
А2 – попал второй стрелок,
А3 – попал 3-й стрелок.
Эти события будут независимыми. Событие А,
состоящее в том, что попали все три стрелка,
выразится как произведение событий А1, А2 и А3 :
А=А1А2А3

9.

P(A)=P(А1А2А3)=P(А1)P(A2)P(A3)=0.9*0.8*0.7=0.504

10.

Три стрелка стреляют по мишени.
Вероятности попадания в цель
для первого, второго и третьего
стрелков равны 0,9; 0,8 и 0,7. Найти
вероятности событий:
В – все стрелки промахнулись

11.

В – все стрелки промахнулись
B A1 A2 A3
P ( B ) P ( A1 ) P( A2 ) P( A3 )
(1 0.9) (1 0.8) (1 0.7)
0.1 0.2 0.3 0.006

12.

Три стрелка стреляют по мишени.
Вероятности попадания в цель
для первого, второго и третьего
стрелков равны 0,9; 0,8 и 0,7. Найти
вероятности событий:
С – попал только второй стрелок

13.

С – попал только второй стрелок
C A1 A2 A3
P(C ) P ( A1 ) P( A2 ) P( A3 )
(1 0.9) 0.8 (1 0.7)
0.1 0.8 0.3 0.024

14.

Три стрелка стреляют по мишени.
Вероятности попадания в цель
для первого, второго и третьего
стрелков равны 0,9; 0,8 и 0,7. Найти
вероятности событий:
D – попал ровно один стрелок

15.

D – попал ровно один стрелок
D A1 A2 A3 A1 A2 A3 A1 A2 A3
P( D) P( A1 A2 A3 ) P( A1 A2 A3 ) P( A1 A2 A3 )
P ( A1 ) P( A2 ) P( A3 ) P( A1 ) P( A2 ) P( A3 ) P( A1 ) P( A2 ) P( A3 )
0.9 0.2 0.3 0.1 0.8 0.3 0.1 0.2 0.7 0.054 0.024 0.014
0.092

16.

Три стрелка стреляют по мишени.
Вероятности попадания в цель
для первого, второго и третьего
стрелков равны 0,9; 0,8 и 0,7. Найти
вероятности событий:
E – попало ровно два стрелка

17.

E – попало ровно два стрелка
E A1 A2 A3 A1 A2 A3 A1 A2 A3
P( E ) P ( A1 A2 A3 ) P ( A1 A2 A3 ) P( A1 A2 A3 )
0.1 0.8 0.7 0.9 0.2 0.7 0.9 0.8 0.3
0.056 0.126 0.216 0.398

18.

Три стрелка стреляют по мишени.
Вероятности попадания в цель
для первого, второго и третьего
стрелков равны 0,9; 0,8 и 0,7. Найти
вероятности событий:
F – попал хотя бы один стрелок

19.

F – попал хотя бы один стрелок
F
- Все стрелки промахнулись
F A1 A2 A3
P( F ) P( A1 A2 A3 ) 0.1 0.2 0.3 0.006
P( F ) 1 P( F ) 1 0.006 0.994

20.

Вероятность того, что потребитель увидит рекламу
определенного продукта в каталоге, равна 0,1. Вероятность
того, что потребитель увидит рекламу того же продукта на
рекламном стенде, равна 0,04. Предполагается, что оба
события независимы. Чему равна вероятность того, что
•А) потребитель увидит обе рекламы
•Б) потребитель увидит только рекламу в каталоге
•В) потребитель увидит рекламу только на стенде
•В) потребитель не увидит рекламы этого товара
•Г) потребитель увидит хотя бы одну рекламу

21.

Вероятность того, что потребитель увидит рекламу
определенного продукта в каталоге, равна 0,1. Вероятность
того, что потребитель увидит рекламу того же продукта на
рекламном стенде, равна 0,04. Предполагается, что оба
события независимы. Чему равна вероятность того, что
•А) потребитель увидит обе рекламы
•Б) потребитель увидит только рекламу в каталоге
•В) потребитель увидит рекламу только на стенде
•В) потребитель не увидит рекламы этого товара
•Г) потребитель увидит хотя бы одну рекламу

22.

Покупатель может приобрести акции трех компаний: А, В
и С. В течение следующего года надежность первой
компании оценивается экспертами в 0,9%, второй – в
0,7%, третьей – 0,8%. Чему равна вероятность того, что
а) все три компании станут банкротами?
Б) ни одна компания не обанкротится
В) обанкротится только компания А
Г) обанкротятся компания А и компания С
в) только одна компания в течение следующего года
станет банкротом
г) две компании обанкротятся
д) хотя бы одна компания не обанкротится
е) хотя бы одна компания обанкротится

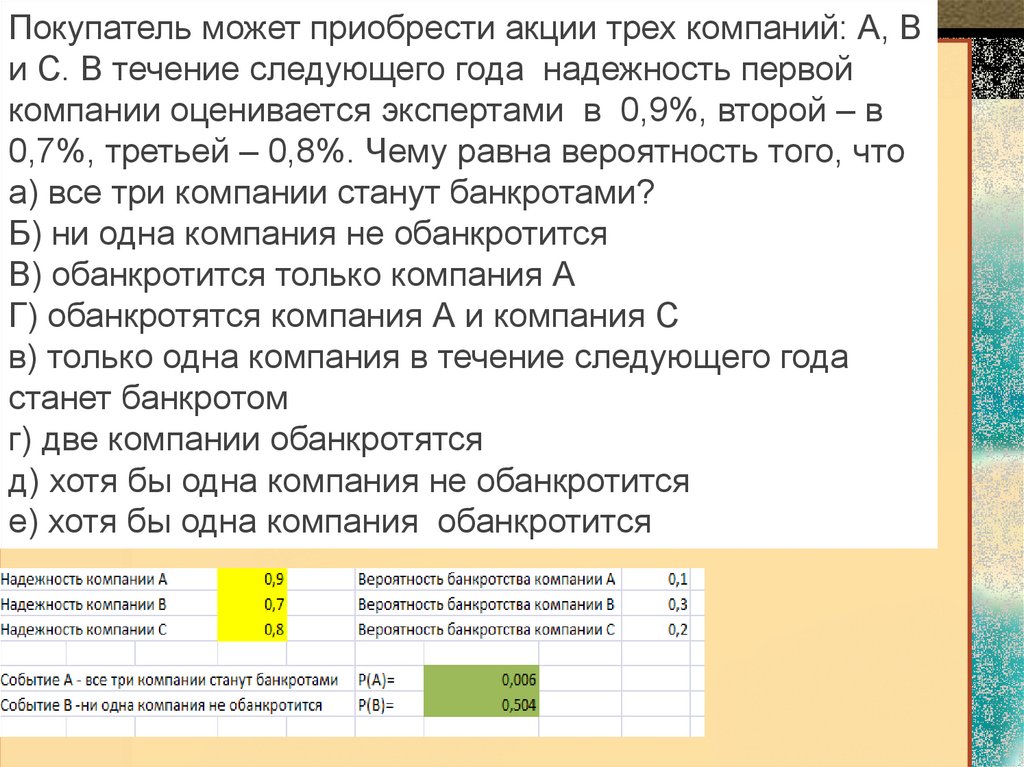
23.

Покупатель может приобрести акции трех компаний: А, В
и С. В течение следующего года надежность первой
компании оценивается экспертами в 0,9%, второй – в
0,7%, третьей – 0,8%. Чему равна вероятность того, что
а) все три компании станут банкротами?
Б) ни одна компания не обанкротится
В) обанкротится только компания А
Г) обанкротятся компания А и компания С
в) только одна компания в течение следующего года
станет банкротом
г) две компании обанкротятся
д) хотя бы одна компания не обанкротится
е) хотя бы одна компания обанкротится