Геометрическая вероятность

1.

В классическом определении вероятности .
m
P( A)
n
Всегда ли можно подсчитать число элементарных
исходов?

2.

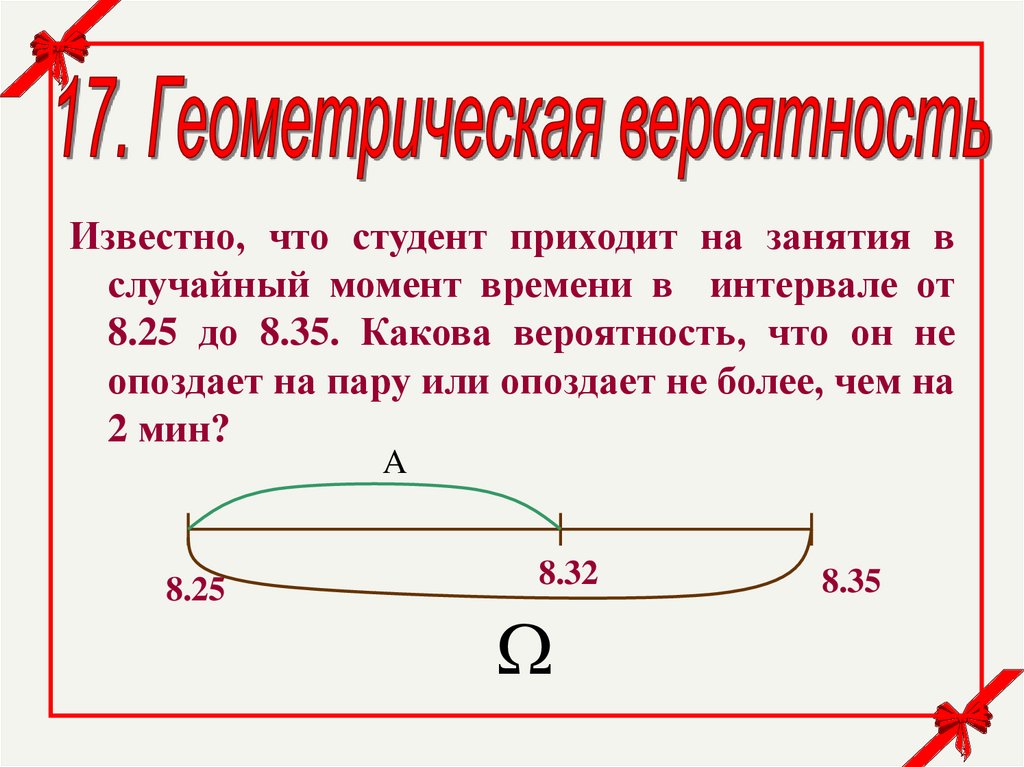
Известно, что студент приходит на занятия в
случайный момент времени в интервале от
8.25 до 8.35. Какова вероятность, что он
опоздает на пару не более, чем на 2 мин?

3.

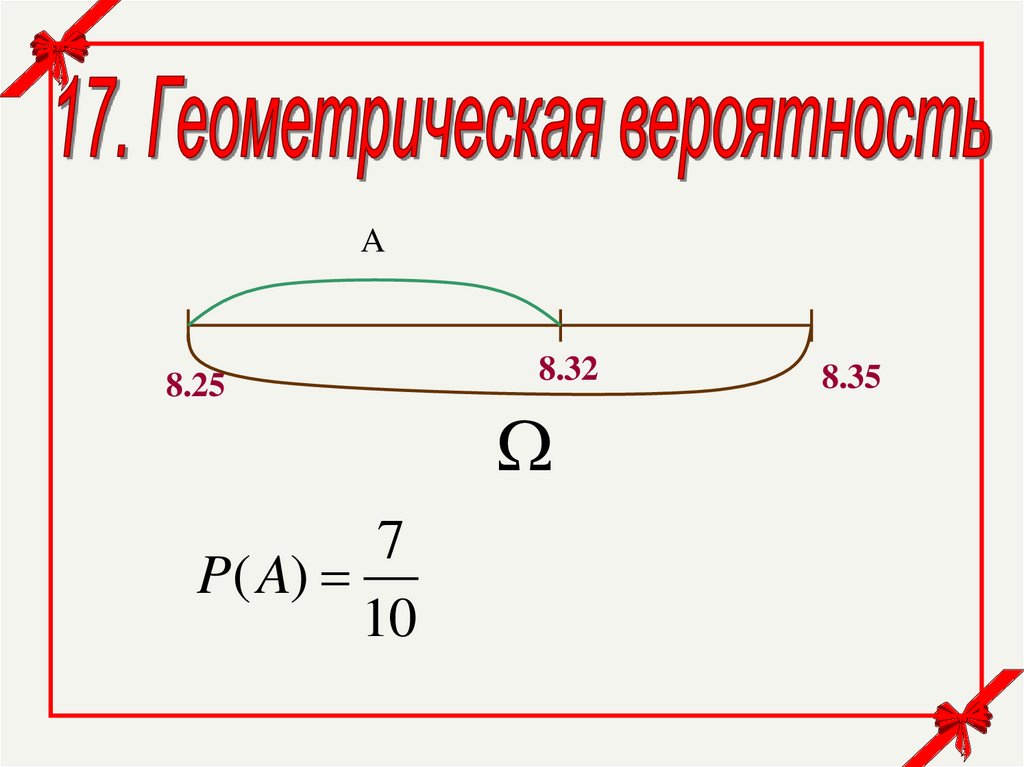
Известно, что студент приходит на занятия в
случайный момент времени в интервале от
8.25 до 8.35. Какова вероятность, что он не
опоздает на пару или опоздает не более, чем на
2 мин?
A
8.25
8.32
8.35

4.

A
8.25
7
P( A)
10
8.32
8.35

5.

Пусть Ω – пространство элементарных исходов,
A – некоторое событие (подмножество Ω). Тогда
P( A)
где
A
A - мера события А.
-мера пространства элементарных
исходов.
Если одномерное пространство, то мерой является длина,
если двумерное, то площадь.

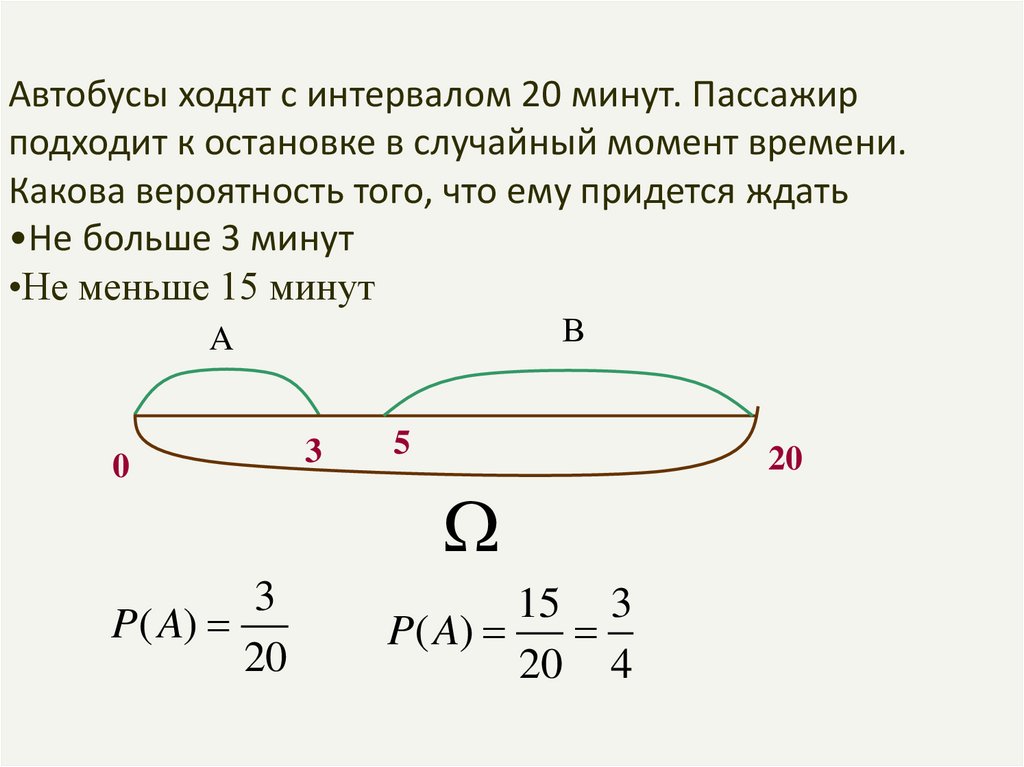
6.

Автобусы ходят с интервалом 20 минут. Пассажир
подходит к остановке в случайный момент времени.
Какова вероятность того, что ему придется ждать
•Не больше 3 минут
•Не меньше 15 минут

7.

Автобусы ходят с интервалом 20 минут. Пассажир
подходит к остановке в случайный момент времени.
Какова вероятность того, что ему придется ждать
•Не больше 3 минут
•Не меньше 15 минут
В
A
0
3
P( A)
20
3
5
15 3
P( A)
20 4
20

8.

Пример После бури на участке между 40-м и
70-м километрами телефонной линии
произошёл
обрыв
провода.
Какова
вероятность того, что он произошёл между
50-м и 55-м километрами линии?

9.

Пример Производится стрельба по круглой
мишени радиуса R. Считая, что попадания в
любую точку мишени равновозможно, найти
вероятность того, что расстояние от точки
попадания до центра мишени не больше r.

10.

Пример Производится стрельба по круглой
мишени радиуса R. Считая, что попадания в
любую точку мишени равновозможно, найти
вероятность того, что расстояние от точки
попадания до центра мишени не больше r.
R2
R

11.

Пример Производится стрельба по круглой
мишени радиуса R. Считая, что попадания в
любую точку мишени равновозможно, найти
вероятность того, что расстояние от точки
попадания до центра мишени не больше r.
R2
r
A
R
A r2

12.

Пример Производится стрельба по круглой
мишени радиуса R. Считая, что попадания в
любую точку мишени равновозможно, найти
вероятность того, что расстояние от точки
попадания до центра мишени не больше r.
R2
r
A
R
A r2
r2
P( A)
2
R
A

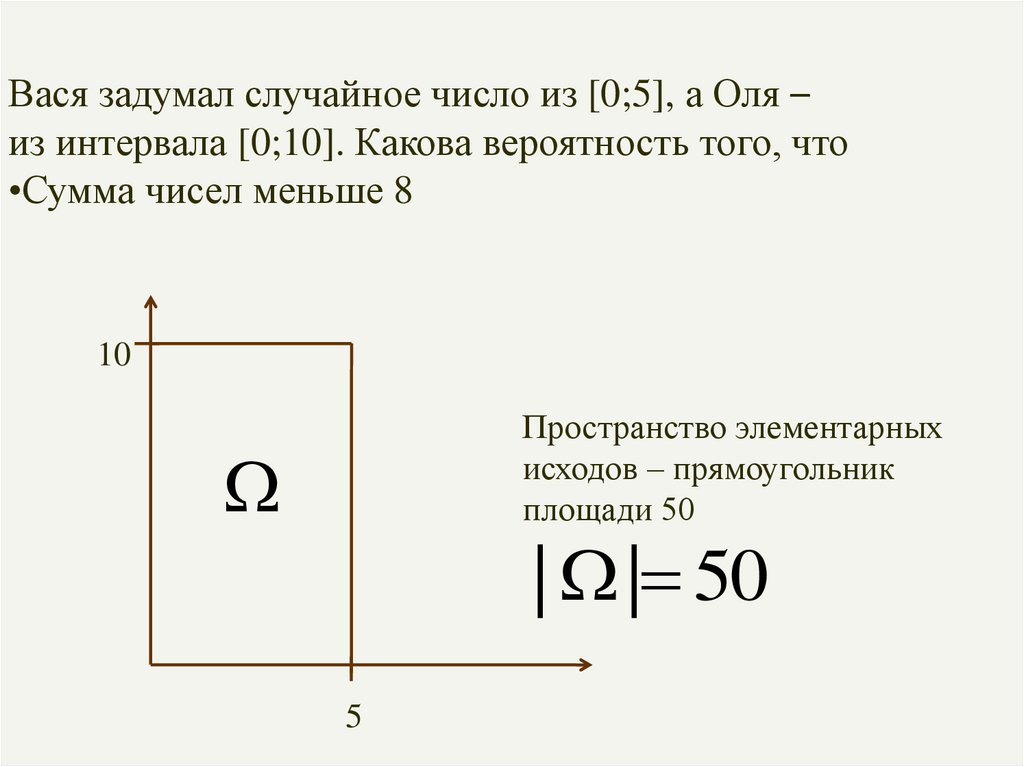
13.

Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Сумма чисел меньше 8
•Произведение чисел меньше 12

14.

Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Сумма чисел меньше 8
10
Пространство элементарных
исходов – прямоугольник
площади 50
| | 50
5

15.

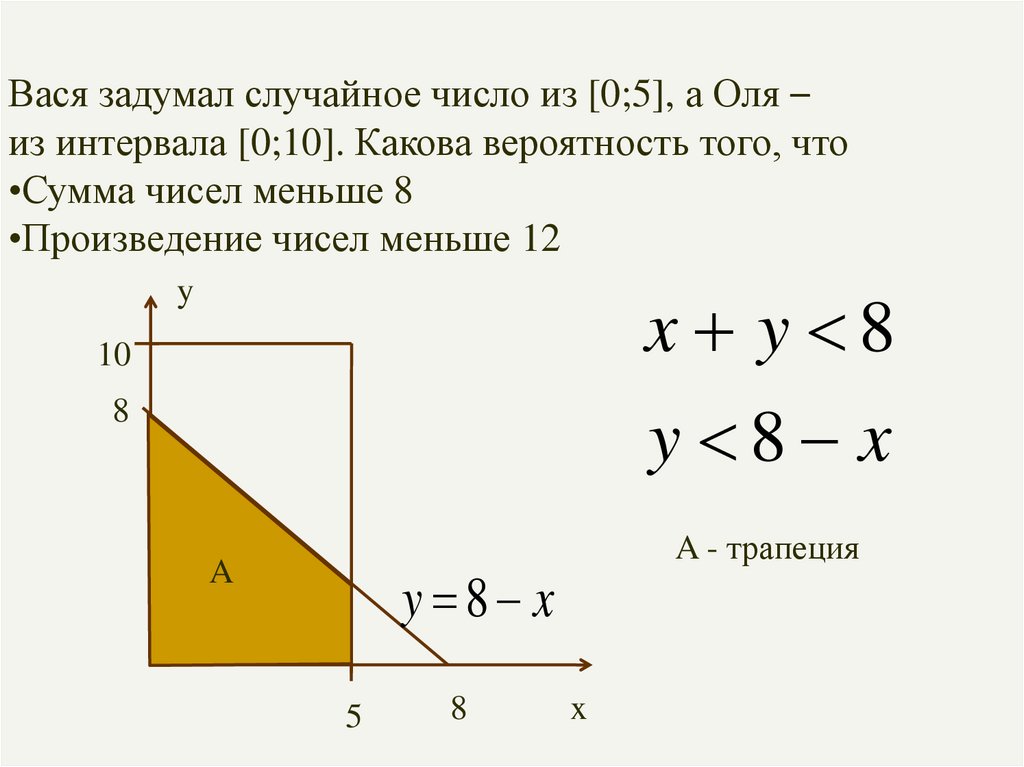
Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Сумма чисел меньше 8
•Произведение чисел меньше 12
y
x y 8
10
y 8 x
8
A
A - трапеция
y 8 x
5
8
x

16.

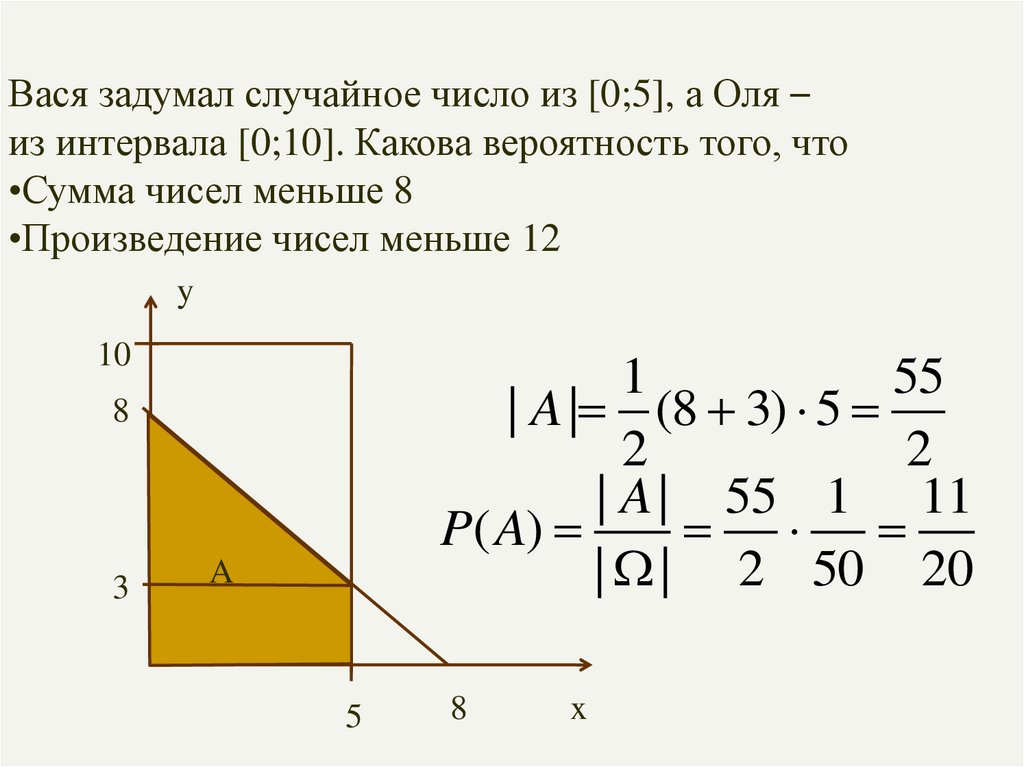
Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Сумма чисел меньше 8
•Произведение чисел меньше 12
y
10
1
55
| A | (8 3) 5
2
2
| A | 55 1 11
P( A)
| | 2 50 20
8
3
A
5
8
x

17.

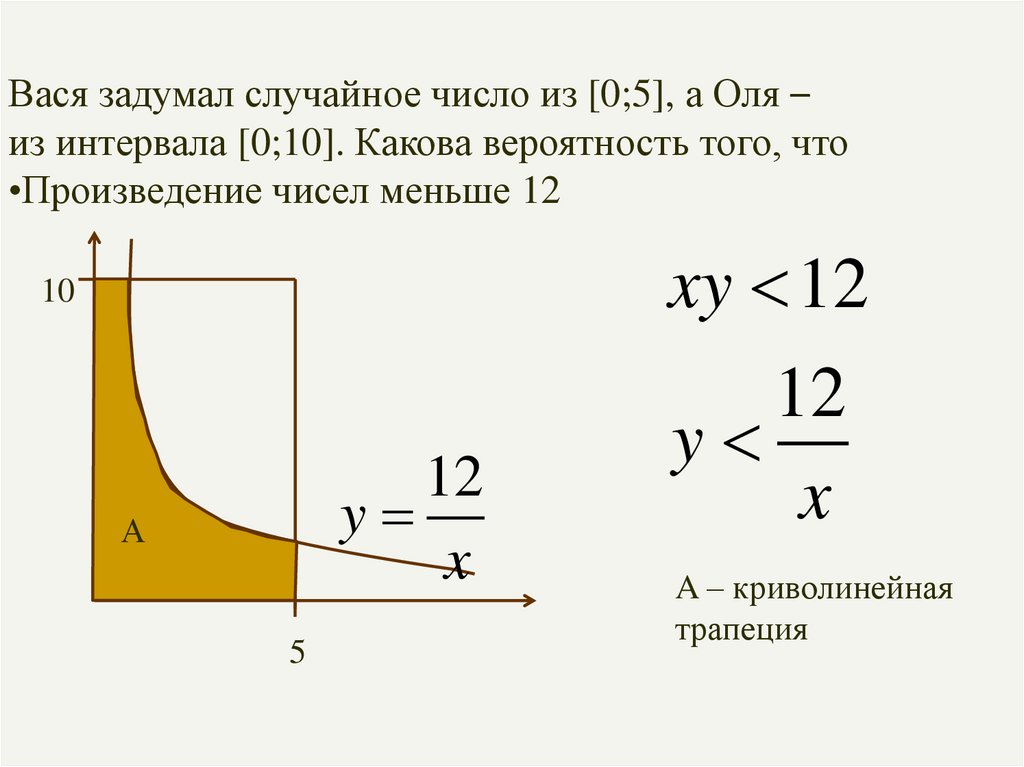
Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Произведение чисел меньше 12
xy 12
10
12
y
x
А
5
12
y
x
A – криволинейная
трапеция

18.

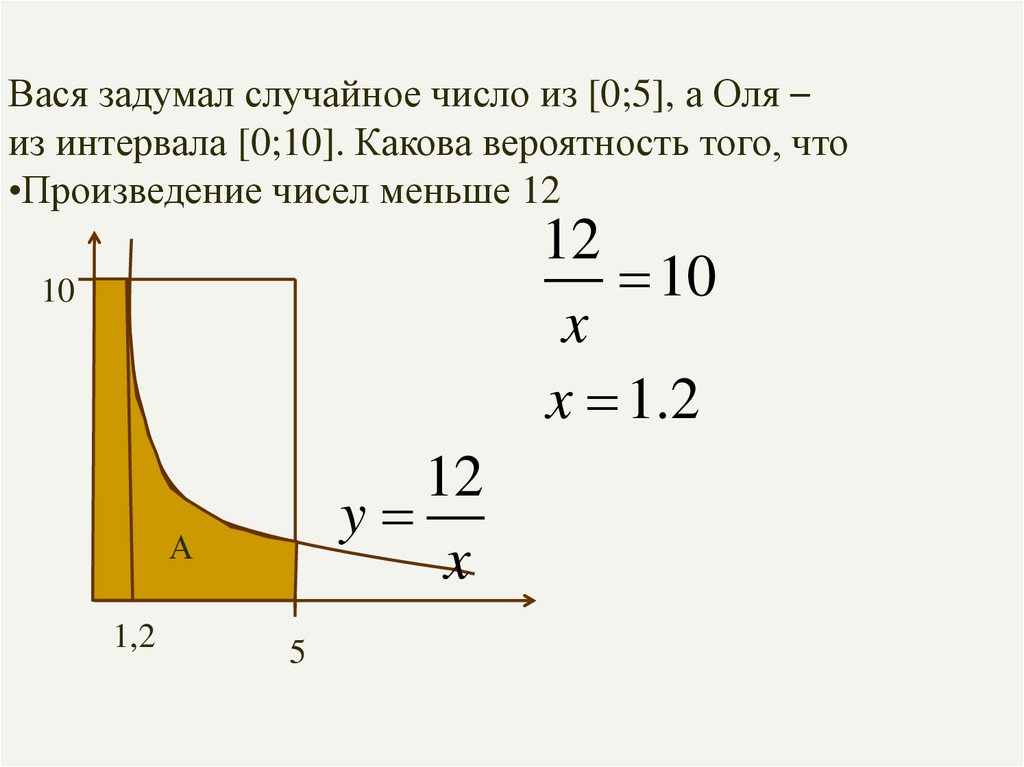
Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Произведение чисел меньше 12
12
10
x
x 1.2
10
12
y
x
А
1,2
5

19.

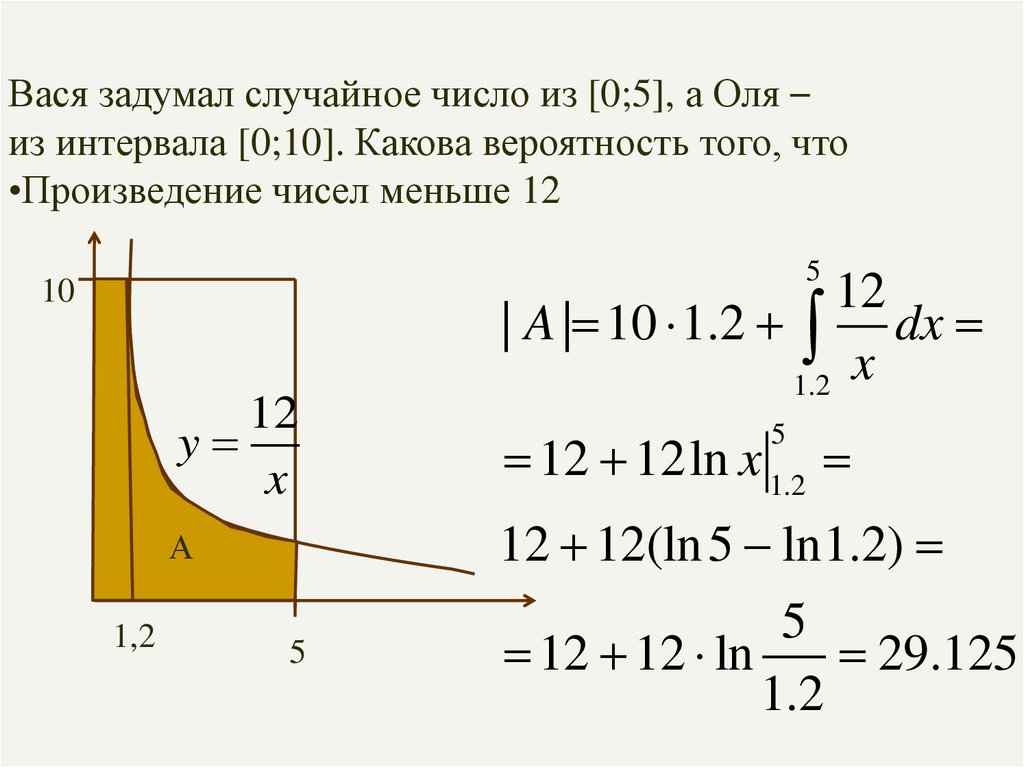
Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Произведение чисел меньше 12
5
10
12
y
x
12 12ln x 1.2
5
12 12(ln 5 ln1.2)
А
1,2
12
| A | 10 1.2 dx
x
1.2
5
5
12 12 ln
29.125
1.2

20.

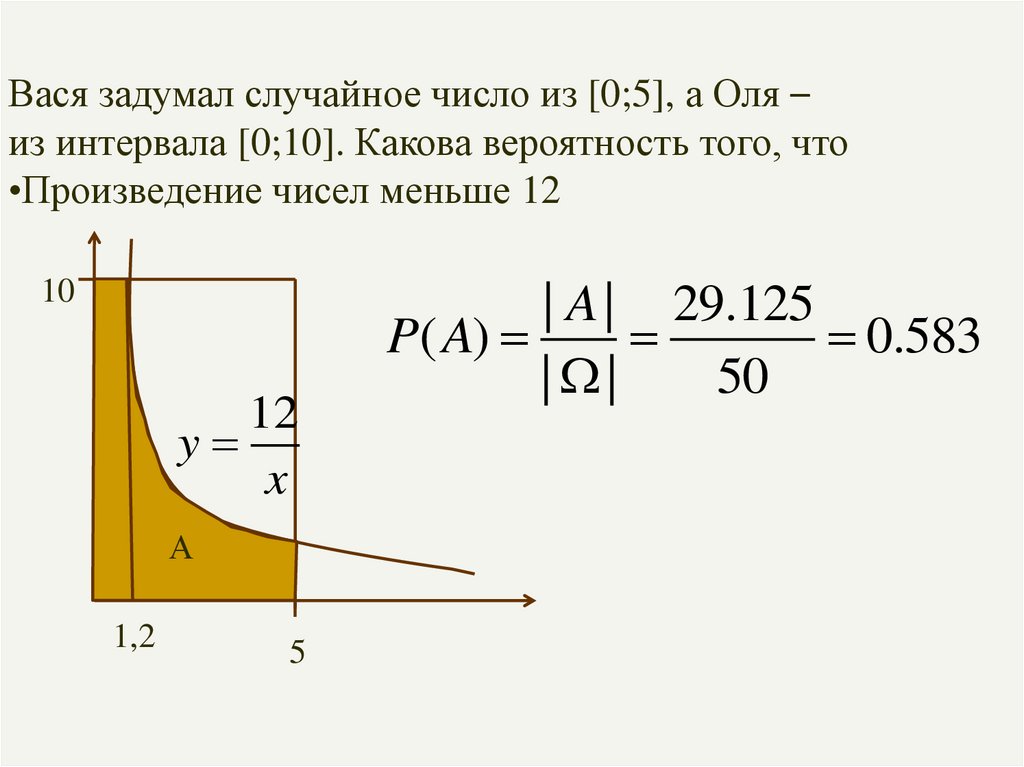
Вася задумал случайное число из [0;5], а Оля –
из интервала [0;10]. Какова вероятность того, что
•Произведение чисел меньше 12
10
12
y
x
А
1,2
5
| A | 29.125
P( A)
0.583
| |
50

21.

Пример
Студенты
случайным
образом
приходят в столовую с 14.00 до 15.00, при
этом обед каждого из них занимает примерно
20 минут. Найти вероятность того, что: а)
Коля встретится с Олей во время обеда, б)
данная встреча не состоится.