Комплексные числа. Основные понятия. Формы записи

1. Комплексные числа. Основные понятия. Формы записи.

Преподаватель: Божкова О.В.
1

2. «Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием» Г. Лейбниц.

2

3. Как все начиналось… (из истории комплексных чисел)

16 век. Италия. Математический турнир между Фиоре и Никколо Тарталья.
Надо решить 30 уравнений третьей степени.
Решение некоторых знал Фиоре от своего учителя – профессора Болонского
университета дель Ферро.
Победил Тарталья, предложив общий вид решения этих уравнений. (Надо
допустить существование некоторого числа квадрат которого равен -1)
17 век. Рене Декарт ввел название «мнимые числа»
18 век Леонард Эйлер ввел обозначение мнимой единицы, предложив
использовать первую букву французского слова imaginare (мнимый).
19 век. Карл Гаусс ввел название комплексные числа, дал им геометрическую
интерпретацию и доказал основную теорему алгебры, утверждающую, что
каждый многочлен имеет хотя бы один действительный или мнимый
корень
x ax b
3
i 1
2
3

4. Определение комплексного числа.

а и в – действительные числа,
i- мнимая единица, квадрат которой равен -1
4

5. Если а=0, то число чисто мнимое. Если в=0,то число действительное.

а=Re z
b=im z
5

6. Числа a+bi и a-bi комплексно – сопряженнные.

6

7. Действия над комплексными числами z1= a1+b1i и z2= a2+b2i

Сложение: z1+z2= (a1+ a2 )+(b1+b2)i
Вычитание: z1-z2= (a1- a2 )+(b1-b2)i
Умножение: z1*z2=(a1a2 - b1b2)+(a1b2+ a2 b1 )i
Умножение комплексно – сопряженных
чисел: z * ž=
• Деление:
7

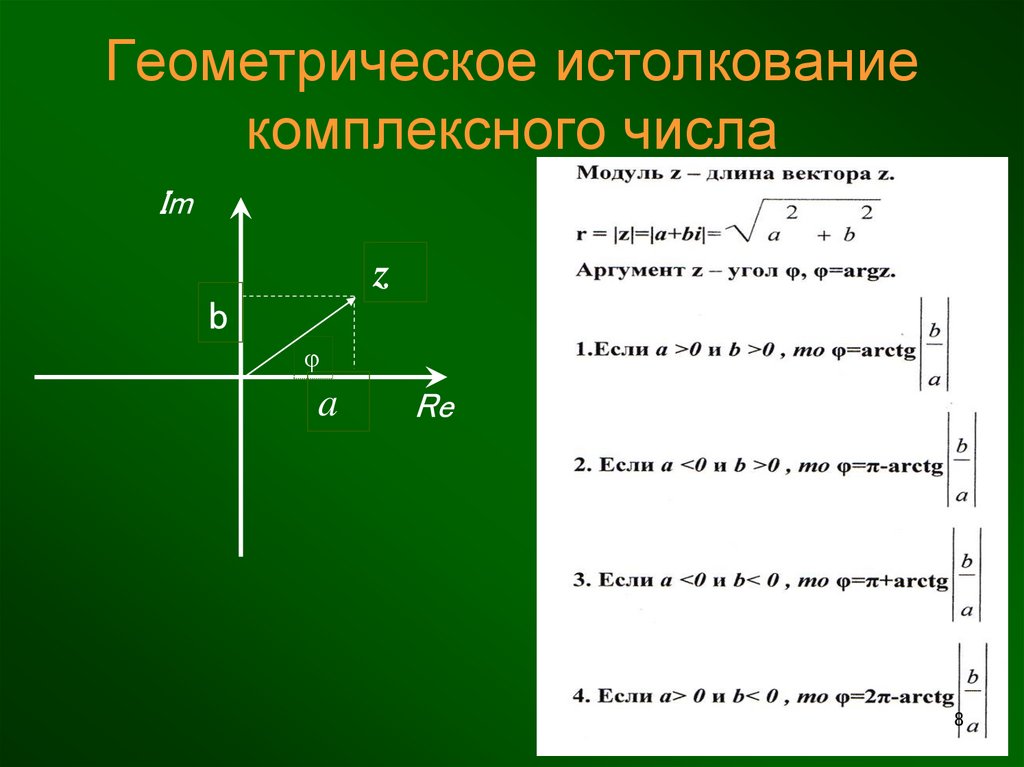
8. Геометрическое истолкование комплексного числа

Im
z
b
φ
a
Re
8

9. Устная работа

1) ImZ = 2
2) ReZ = -1
3) ImZ >0
4) ReZ ≤ 3
Im
Im
б)
Im
а)
2i
i
Re
Re
в)
3 Re
г)
-1
Im
Re
9

10. Формы записи комплексных чисел

• Алгебраическая z=a+bi
• Тригонометрическая( а =rcosφ,
b=rsin φ) z=r(cosφ +isin φ)
• Показательная
10

11. Показательная форма записи комплексного числа.

• Формула Эйлера
=cosφ +isin φ
• Показательная форма
z=r
11

12. Переход от одной формы к другой

Задание:
1.Записать комплексное число z=-1+i в
тригонометрической и показательной
формах.
2.Ответ проверить обратным переходом
12

13. Действия над комплексными числами в тригонометрической и показательной формах.

Тригонометрическая
Показательная
1.Умножение
2.Деление
3. Возведение в
степень
13

14. Действия над комплексными числами

• Возведение в степень
14

15. Математический шедевр

• В формулу Эйлера
подставить φ=π
15

16. Всем большое спасибо!!!

16