Выпуклый анализ. Минимум выпуклой функции. Лекция 16

1. ВЫПУКЛЫЙ АНАЛИЗ

ЛЕКЦИЯ 16
5. МИНИМУМ ВЫПУКЛОЙ ФУНКЦИИ

2.

5. МИНИМУМ ВЫПУКЛОЙ ФУНКЦИИ
5.1. Локальный и глобальный минимум выпуклой функции.
5.2. Минимум дифференцируемой выпуклой функции.
5.3. Минимум выпуклой функции, дифференцируемой
по всем возможным направлениям.

3.

5.1. Локальный и глобальный минимум выпуклой функции. Выпуклые функции
представляют собой удобные объекты исследования для анализа их значений на минимум.
Это объясняется тем обстоятельством, что выпуклые функции не могут иметь локальных
минимумов.
1
Теорема 1. Пусть функция I : U ® R , где U R
n
выпуклое множество,
выпукла. Тогда всякая точка локального минимума функции
I
на множестве
U
одновременно является точкой ее глобального минимума на этом множестве, причем
множество
U u U I (u ) min I (u ) I
u U
выпукло. В случае, когда функция
I
строго выпукла на
U , множество U
содержит не более одной точки.
Доказательство.
на множестве
U.
Пусть
u
точка локального минимума функции
Тогда существует окрестность
I
O u , точки u , что

4.

U
выполнено
u
O u ,
I (u ) £ I (u ), "u O u , I U .
Для любого
u U
и достаточно малого
0,1
будет
u -u <
u - u < Þ u + u - u O u , .
С другой стороны,
U
U
U имеем u + u - u u + 1 - u U .
u + 1 - u O u , I U . В силу того, что u - точка
в силу выпуклости множества
Таким образом,
локального минимума
и из выпуклости функции
I
следует
O u , I U
æ
6
44
7 4 48 ö
U
I ( u ) £ I ç u + u - u ÷ I u + 1 - u £ I u + 1 - I (u )
çç
÷÷
или
è
ø
I (u ) £ I u + I (u ) - I (u ) Þ I (u ) £ I (u ), " u U Þ u U .
Таким образом, всякий локальный минимум одновременно является глобальным.
Пусть теперь
u , v U
и
0,1 . Тогда
I
I
I £ I u + 1 - v £ I u + 1 - I v I + 1 - I I .
1

5.

I u + 1 - v I Þ u + 1 - v U ,
и множество
U
выпукло. Если
u ¹ v ,
то для строго выпуклых функций
неравенство (1)
I £ I u + 1 - v £ I u + 1 - I v I + 1 - I I .
не может превратиться в равенство
1
I u + 1 - v I
0,1 . Следовательно, строго выпуклая функция не может
при
достигать минимума на выпуклом множестве более чем в одной точке. Теорема
доказана.
5.2. Минимум дифференцируемой выпуклой функции.
Выведем условия, которым
должна удовлетворять точка минимума, выпуклой дифференцируемой функции.
1
Теорема 2. Пусть функция I : U ® R , где
и I C U . Тогда в любой точке
1
u U
U R n – выпуклое множество,
выполняется неравенство
I '(u ), u - u ³ 0, " u U ,
а в случае
u int U ,
равенство
I '(u ) 0.
1
Кроме того, если функция
I

6.

выпукла на множестве
U,
I '(u ), u - u ³ 0, " u U
то условие (1)
u U .
достаточным для того, чтобы
Доказательство. Необходимость. Пусть
u U .
1
Для всех u U ,
является
0,1
имеем
I C U
1
0 £ I u + 1 - u - I (u ) I u + u - u - I (u )
I C1 U
I ' u , u - u
é
o ù
+ o ê I ' u , u - u +
úÞ
û
ë
0
o
I ' u , u - u +
³ 0.
В последнем неравенстве устремим число 0,1 к нулю. В пределе получим
неравенство (1). I '(u ), u - u ³ 0, " u U
1
u int U , то для любого вектора e R n , e 1 найдется число 0 > 0,
u u + e U , " 0, 0 . В неравенстве (1) полагаем u u + e. Тогда
Если
что
u + e
>0
I '(u ), u - u I '(u ), u + e - u × I ' u , e ³ 0 Þ I ' u , e ³ 0
В силу произвольности
Необходимость доказана.
e Rn , e 1
отсюда выводим, что
I ' u 0.

7.

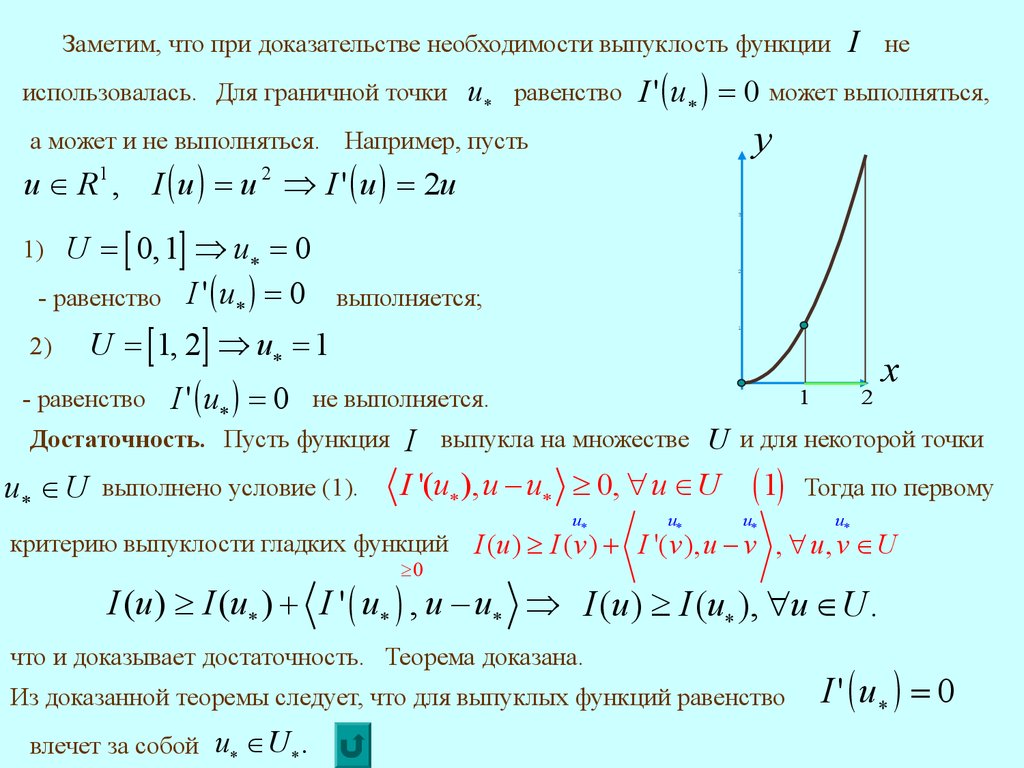
Заметим, что при доказательстве необходимости выпуклость функции
использовалась. Для граничной точки
u равенство I ' u 0 может выполняться,
а может и не выполняться. Например, пусть
u R 1 , I u u 2 Þ I ' u 2u
U 0, 1 Þ u 0
- равенство I ' u 0
I не
4
y
3
1)
2)
2
выполняется;
U 1, 2 Þ u 1
- равенство
I ' u 0
не выполняется.
Достаточность. Пусть функция
u U
1
выполнено условие (1).
1
I выпукла на множестве U
I '(u ), u - u ³ 0, " u U
u
u
2
x
и для некоторой точки
1
u
Тогда по первому
u
критерию выпуклости гладких функций I (u ) ³ I ( v ) + I '( v ), u - v , " u , v U
³0
I (u ) ³ I (u ) + I ' u , u - u Þ I (u ) ³ I (u ), "u U .
что и доказывает достаточность. Теорема доказана.
Из доказанной теоремы следует, что для выпуклых функций равенство
влечет за собой
u U .
I ' u 0

8.

5.3. Минимум выпуклой функции, дифференцируемой по всем возможным
направлениям. Требование существования производных по направлениям существенно
менее жесткое, чем требование дифференцируемости. В связи с этим представляет
интерес получить условия оптимальности в терминах производных по направлению.
Это тем более естественно, поскольку всякая выпуклая функция в любой внутренней точке
области определения имеет производные по всем направлениям.
Теорема 3. Пусть I
: U ® R1 , где U R n выпуклое множество, U U
множество точек минимума функции
функция
I
на множестве
U
и в точке
u U
имеет производные по всем возможным направлениям. Тогда необходимо
выполняется условие
dI
u ³ 0
de
для всех возможных направлений
I
I
выпукла на
U,
e e 1
1
в точке
u .
Кроме того, если функция
то это условие достаточно для u U .

9.

Доказательство. Необходимость.
направление в точке
u .
Пусть u U и e e 1 - возможное
Тогда
I u + te - I u
I u + te ³ I u Þ
³ 0, 0 < t £ t0 ,
t
t 0 достаточно мало. Переходя в (2) к пределу при t ® 0, получим (1).
U
где
dI
u ³ 0
de
1
Необходимость доказана.
Достаточность. Пусть
I : U ® R1
- выпуклая функция и в некоторой точке
u U выполнено условие (1). Возьмем любую точку u U , u ¹ u
u - u
e
.
u - u
2
Направление
e
возможное в точке
и положим
u U . Действительно, при
t
малых t > 0, для которых выполнено
£ 1, имеем
u - u
u - u
1
64 7 £4
8
u + 1- u
u - u
6
44
7 4 48
}
t
u - u
u - u u + u - u U ,
u + t e u + t ×
u +
u - u
u - u

10.

f (t ) I u + te , t 0, t0 , t0 u - u .
Полагаем
Функция
f : 0, t0 ® R1
0,1 , t1 , t2 0, t0
является выпуклой. Действительно,
для всех
имеем
6 4 4 7t 4 48 ö
æ
æ 6 44 7t 4 48 ö
f ç t1 + 1 - t2 ÷ I ç u + t1 + 1 - t2 e ÷
ç
÷
ç
÷
è
ø
è
ø
I u + 1 - u + t1 + 1 - t2 e
I u
f t1
+ t1e + 1 - u + t2e
Iвыпукла
-
£
f t2
64 7 48
6 4 7 48
£ I u + t1e + 1 - I u + t2e f t1 + 1 - f t2 .
Выпуклость функции
f (t )
f (0)
f '(0)
f
доказана. Тогда по первому критерию выпуклости
t -0
I (u ) ³ I (v) + I '(v), u - v
выводим
dI
u ³ 0 1
de
}
f (t ) ³ f (0) + f '(0) × t - 0 ³ 0 Þ f (t ) - f (0) ³ f '(0) × t ³ 0 Þ
f (t ) ³ f (0), "t 0, t0 .

11.

f (t ) ³ f (0), "t 0, t0 .
В частности,
u -u
æ
ö
u -u u -u
ç
÷
f (t0 ) I ç u + t0 × e ÷
ç
÷
è
ø
f (t0 ) ³ f (0).
Заметим, что
æ
ö
u - u
I çç u +
u - u ÷÷ I u ,
u - u
è
ø
f (0) I u* .
I (u )
I u
f (t0 ) ³ f (0) Þ I (u ) ³ I u "u U , что и требовалось доказать.
В частности, если в точке u существует градиент I ' u , то для направления
u - u
e
, u U , u ¹ u имеем
u - u
Тогда
I ' u , e
678
dI
u
de
u -u
u -u
}
I ' u , e
u - u
I ' u ,
u - u
1
u - u
I ' u , u - u Þ

12.

64 7³ 048
dI
1
u
I ' u , u - u
de
u - u
Тогда
6 4 7 1 48
dI
u ³ 0 Û
de
Получили формулировку теоремы 2.
I ' u , u - u ³ 0.
I ' u , u - u ³ 0
Таким образом, теорема 3
является обобщением теоремы 2 на существенно более широкий класс функций
(функций дифференцируемых по всем возможным направлениям).
Упражнение.
Точка
определенной формулой
u 0 является точкой минимума функции I : R n ® R1 ,
I u u .
Доказать непосредственно, что эта точка и только она удовлетворяет неравенству
для всех возможных направлений
e
dI
u ³ 0
de
e 1 .

13.

Решение.
I u u
поэтому ее производную по направлению e
В точке
u 0
функция
определению этой производной
дифференцируемая только по направлению,
вычисляем непосредственно по
0 + te
64 7 48 }0
te
I 0 + te - I (0)
dI
e 1.
lim
u tlim
t ®+0 t
®+0
de
t
u 0
dI
Таким образом,
u 1 > 0, " e 1.
de
u 0
u R n любое направление e будет возможным. Вычислим
производную по направлению e от функции I u u в произвольной точке
Для любой точки
u ¹ 0.
I ' u
В этих точках функция является дифференцируемой, поэтому
¶
u, u
¶u
u
u, u
u
Þ
u
u, e
dI
u I ' u , e u .
de

14.

Покажем, что для любого
u R ,u ¹ 0
n
dI
u ³ 0 "e,
de
Действительно, пусть
Направление
e1 -e
u R n , u ¹ 0.
невозможно
e 1.
В силу
u ¹ 0 найдется e,
что
также допустимо. Тогда одна из производных
-e
u, e
dI
dI
u
,
u
de
u
de1
должна быть строго отрицательной.
u , e1
u
u, e
.
u
e, u ¹ 0.