Выпуклый анализ. Выпуклые функции. Лекция 11

1. ВЫПУКЛЫЙ АНАЛИЗ

ЛЕКЦИЯ 11
3. ВЫПУКЛЫЕ ФУНКЦИИ.

2.

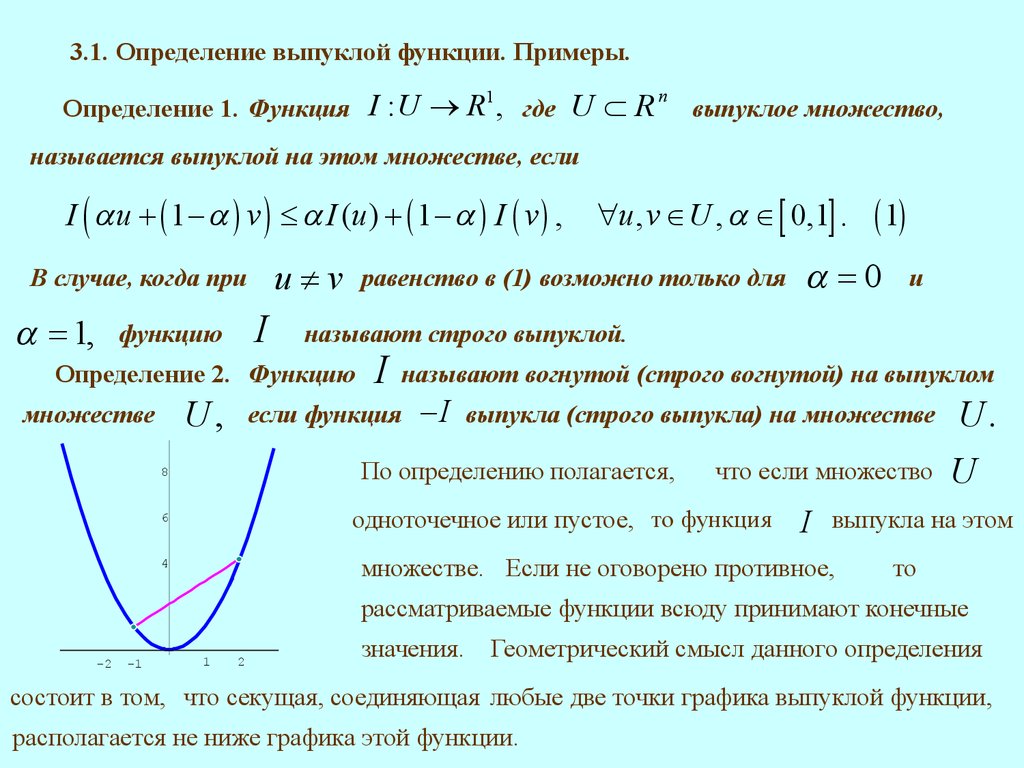
3. ВЫПУКЛЫЕ ФУНКЦИИ
3.1. Определение выпуклой функции. Примеры.
3.2. Действия с выпуклыми функциями.

3.

3.1. Определение выпуклой функции. Примеры.
Определение 1. Функция I : U ® R , где
1
U R n выпуклое множество,
называется выпуклой на этом множестве, если
I ( a u + ( 1 - a ) v ) £ a I (u ) + ( 1 - a ) I ( v ) ,
u v
В случае, когда при
a 1,
I
функцию
равенство в (1) возможно только для
U,
I
-I
что если множество
одноточечное или пустое, то функция
I
U.
U
выпукла на этом
множестве. Если не оговорено противное,
4
и
выпукла (строго выпукла) на множестве
По определению полагается,
6
a 0
называют вогнутой (строго вогнутой) на выпуклом
если функция
8
( 1)
называют строго выпуклой.
Определение 2. Функцию
множестве
"u, v Î U , a Î [ 0,1] .
то
рассматриваемые функции всюду принимают конечные
-2
-1
1
2
значения.
Геометрический смысл данного определения
состоит в том, что секущая, соединяющая любые две точки графика выпуклой функции,
располагается не ниже графика этой функции.

4.

Пример 1. Функция I : R ® R , определенная формулой
n
Действительно, при всех
1
u, v Î R n , a Î [ 0,1]
I (u ) u ,
выпукла.
имеем
I ( a u + ( 1 - a ) v ) a u + ( 1 - a ) v £ a u + (1 - a ) v a I (u ) + ( 1 - a ) I (v).
Пример 2. Функция
I : R n ® R1 ,
выпукла. Действительно, при всех
определенная формулой I (u ) c, u , c Î R ,
n
u, v Î R n , a Î [ 0,1]
имеем
I ( a u + ( 1 - a ) v ) c, a u + ( 1 - a ) v a c, u + ( 1 - a ) c, v
a I (u ) + ( 1 - a ) I (v).
Аналогично проверяется выпуклость функции
функция
I
- I . Таким образом, в данном примере
выпукла и вогнута одновременно.
Пример 3. Функция I : R n ® R1 , определенная формулой I (u )
u, u ,
строго выпукла. Действительно, при всех u , v Î R n , u v справедливо неравенство
2 u , v < u , u + v, v .

5.

Отсюда для любого
a Î [ 0,1]
выводим
I ( a u + ( 1 - a ) v ) a u + ( 1 - a ) v, a u + ( 1 - a ) v
< u ,u + v ,v , u v
a u, u + 2 u, v
2
<a
2
× a ( 1 - a ) + ( 1 - a ) × v, v <
2
u , u + éë u , u + v, v ùû a ( 1 - a ) + ( 1 - a )
2
v, v
a 2 u , u + a u , u - a 2 u , u + a v, v -
-a 2 v, v + v, v - 2a v, v + a 2 v, v
a u , u + a v, v + v, v - 2a v, v
a u , u + (1 - a ) v, v a I ( u ) + ( 1 - a ) I ( v ) , "u, v Î R n , u v,
I.
что и означает строгую выпуклость функции
Теорема 1. Пусть функция
I : U ® R1 ,
выпукла. Тогда для любых
ui Î U , a i ³ 0, i 1,L , m,
U Rn
где
m
åa
i 1
i
выпуклое множество,
1, m 1, 2,L

6.

имеет место неравенство (Иенсена)
æ m
ö m
I ç å a i ui ÷ £ å a i I ( ui ) .
è i 1
ø i 1
Доказательство. Проведем индукцию по числу m. При
( 2)
m 2 справедливость
неравенства (2) есть следствие определения выпуклости функции. Допустим, что
неравенство Иенсена имеет место для всех
определенности, что
a m 1.
m -1
Тогда
k £ m - 1, m > 2.
åa
i 1
i
1- am > 0
Примем для
и
æ m
ö
æ m -1
ö
I ç å a i ui ÷ I ç å a i ui + a mum ÷
è i 1
ø
è i 1
ø
bi
æ >0 æ 678
ö
ö
ç 64 7 48 ç m -1 a
÷
÷
i
I ç ( 1- am ) ç å
ui ÷ + a mum ÷
i 1 1 - a m
ç
÷
ç
÷÷
ç
ç
÷
è
ø
è
ø
æ
ö
64 7u* 48
ç
÷
æ m -1
ö
I ç ( 1 - a m ) ç å b i ui ÷ + a mum ÷
è i 1
ø
ç
÷
ç
÷
è
ø
I ( ( 1 - a m ) u* + a mum ) Þ

7.

m -1
ai
æ m
ö
.
I ç å a i ui ÷ I ( ( 1 - a m ) u* + a mum ) , u* å bi ui , bi
1- am
i 1
è i 1
ø
Заметим, что b i ³ 0, i 1,L , m - 1 и
1-a m
}
m -1
m -1
åb
i 1
i
åa
1- am
ai
i 1
1.
å
1- am
1- am
i 1 1 - a m
m -1
i
m -1
Тогда
u* å bi ui Î U
и в силу выпуклости функции
i 1
I
имеет место неравенство
æ m-1
ö
ç bi ui ÷
ç
÷
è i 1
ø
å
}
³0
³0
ææ
ö
ö
I ç ç1 - a m ÷ u* + a m um ÷ £ ( 1 - a m ) I ( u* ) + a m I ( um )
ø
èè
ø
предположение индукции
£
( 1- am )
m-1
å bi I ( ui )
i 1
6 4 7 48
æ m -1
ö
I ç å bi ui ÷
è i 1
ø
+ a m I ( um ) £

8.

æ 1-aai
ö
m
ç m -1 }
÷
£ ( 1 - a m ) ç å bi I ( ui ) ÷ + a m I ( um )
ç i 1
÷
ç
÷
è
ø
æ m -1 a i
ö
æ m -1
ö
( 1- am ) ç å
I ( ui ) ÷ + a m I ( um ) ç å a i I ( ui ) ÷ + a m I ( um )
è i 1
ø
è i 1 1 - a m
ø
m
å a i I ( ui ) .
i 1
Возвращаясь на начало цепочки, получим
æ m
ö
I ç å a i ui ÷ £
è i 1
ø
m
åa I ( u ) .
i 1
i
i
Теорема доказана.
Следующая теорема позволяет свести исследование выпуклости функции многих
переменных к исследованию выпуклости функций одной переменной.

9.

n
I : U ® R1 , где U R выпуклое множество,
1
j
:[0,1]
®
R
,
функция
выпукла тогда и только тогда, когда для любых v , w Î U
Теорема 2. Функция
j (e ) I ( e v + (1 - e ) w ) , e Î [0,1] выпукла.
Доказательство. Необходимость. Пусть функция I выпукла на выпуклом
определенная формулой,
U и v, w Î U . Для любых e1 , e 2 , a Î [ 0,1] полагаем
e a ae1 + ( 1 - a ) e 2 . Вычисляем
( 1-( ae1 +( 1-a ) e 2 ) ) ö
æ ae1 +}( 1-a ) e 2
64 7 48
ç
÷
j ( ea ) I ç ea v + ( 1 - ea ) w ÷
ç
÷
è
ø
множестве
I ( ( ae1 + (1 - a )e 2 ) v + ( 1 - ae1 - (1 - a ) e 2 ) w ± a w )
I ( ae1v + e 2 v - ae 2 v + w - ae1w - e 2 w + a e 2 w +a w - a w )
I ( ae1v - ae1w + a w + e 2 v ( 1 - a ) + ( 1 - a ) w + e 2 w ( a - 1) )
I ( a ( e1v + w - e1w ) + ( 1 - a ) ( e 2 v - e 2 w + w ) )

10.

I ( a ( e1v + w - e1w ) + ( 1 - a ) ( e 2 v - e 2 w + w ) )
ÎU
ÎU
4 48 ö
4 48 ö ö Iвыпуклая
æ æ 6 44 7
æ 6 44 7
I ç a ç e1v + ( 1 - e1 ) w ÷ + ( 1 - a ) ç e 2v + ( 1 - e 2 ) w ÷ ÷ £
÷
ç
÷÷
ç ç
ø
è
øø
è è
j( e )
j ( e1 )
6 4 44 7 4 4 48
6 4 44 7 4 4 48
Iвыпуклая
£ a I ( e1v + ( 1 - e1 ) w ) + ( 1 - a ) I ( e 2v + ( 1 - e 2 ) w )
2
aj (e1 ) + ( 1 - a ) j (e 2 ) Þ
j ( ae1 + (1 - a ) e 2 ) £
aj (e1 ) + ( 1 - a ) j (e 2 ).
Необходимость доказана.
Достаточность. Пусть для любой пары точек
Тогда для всех a Î 0,1 имеем
j( a )
a ×1+ ( 1-a )×0 )
[ ]
6 4 44 7 4 4 48
æ
I ( a u1 + (1 - a )u2 ) j ç
ç
è
неравенство Иенсена
£
Теорема доказана.
}
a
ö
÷
÷
ø
u1 , u2 Î U
j (a ×1 + ( 1 - a ) × 0 )
функция
j
выпукла.
неравенство Иенсена
£
I ( u1 )
I ( u2 )
}
}
a j (1) + ( 1 - a ) j (0) a I (u1 ) + ( 1 - a ) I (u2 ).

11.

Упражнение 1.
Доказать выпуклость функции
I (u ) ( x + y )
Решение.
Пусть
Полагаем
2
æ xö
u ç ÷.
è yø
æ x1 ö
æ x2 ö
u ç ÷ , v ç ÷ , e Î [ 0,1] Þ
è y1 ø
è y2 ø
æ x1 ö
æ x2 ö æ e x1 + ( 1 - e ) x2 ö
eu + ( 1- e ) v e ç ÷ + ( 1- e ) ç ÷ ç
÷
è y1 ø
è y2 ø è e y1 + ( 1 - e ) y2 ø
Тогда
j ( e ) I (e u + ( 1 - e ) v) ( e x1 + ( 1 - e ) x2 + e y1 + ( 1 - e ) y2 )
2
[ e x1 + x2 - e x2 + e y1 + y2 - e y2 ]
2
éë( x1 - x2 + y1 - y2 ) e + x2 + y2 ùû
2

12.

2
678 ù
é6 4 4 7 4 4 8
³0
ê( x1 - x2 + y1 - y2 ) e + x2 + y2 ú a 2 × e 2 + 2ab × e + b 2 j ( e ) .
ê
ú
ë
û
a
Функция j
она выпукла.
: [ 0,1] ® R1
b
представляет собой параболу ветвями вверх и поэтому
По теореме 2 будет выпуклой и исходная функция
I : R 2 ® R1.

13.

3.2. Действия с выпуклыми функциями.
Рассмотрим некоторые операции над
выпуклыми функциями, сохраняющие их выпуклость.
Теорема 3. Пусть функции
выпуклы и
I i : U ® R1 ,
где U
Rn
выпуклое множество,
li ³ 0, i 1,L , m. Тогда функция I : U ® R1 , определенная формулой
m
выпукла.
I (u ) å li I i (u ), u Î U ,
Доказательство. Для любых
i 1
u, v ÎU , a Î [ 0,1]
имеем
I ( au + ( 1-a ) v)
£a I i ( u ) + ( 1-a ) Ii ( v )
6
} 447448
å li I i (a u + ( 1 - a ) v) £
m ³0
i 1
)
6 4 7I (u4
8
æ m
ö
a ç å li I i (u ) ÷ + ( 1 - a )
è i 1
ø
Теорема доказана.
m
å l éëa I (u) + ( 1 - a ) I (v) ùû
i 1
I (v )
i
i
i
64748
æ m
ö a I u + 1 - a I (v).
( ) (
)
ç å li I i (v) ÷
è i 1
ø

14.

Теорема 4. Пусть функции
I i : U ® R1 , i 1,L , m,
выпуклое множество, выпуклы. Тогда функция I
где
U Rn
: U ® R1 , определенная формулой
I (u ) max { I i (u )} , u Î U ,
iÎ{ 1,L , m}
выпукла.
Доказательство. Для любых
u, v ÎU , a Î [ 0,1] имеем
+ (1-a ) I i ( v )
ì 6£a4Ii (4u )7
4 48 ü
ï
ï
I i (a u + ( 1 - a ) v) ý £
I ( a u + ( 1 - a ) v ) iÎmax
í
{ 1,L , m}
ïî
ïþ
£ max { a I i (u ) + (1 - a ) I i (v)} £
iÎ{ 1,L , m}
)
)
6 44 7I (u4
48
6 44 7I ( v4
48
£ a max { I i (u )} + (1 - a ) max { I i (v)}
iÎ{ 1,L , m}
Теорема доказана.
iÎ{ 1,L , m}
a I (u ) + (1 - a ) I (v).

15.

Из доказанной теоремы, в частности следует, что функция
n
определенная на выпуклом множестве U R
равенством
g + : U ® R1 ,
g + (u ) max { g (u ), 0} , u Î U ,
где
g : U ® R1 ,
выпукла на множестве
g.
U,
функция
Теорема 5. Пусть функция j
: [ a, b ] ® R1
g : U ® [ a, b ] , где множество
U Rn
Тогда функция
I : U ® R1 ,
выпукла на множестве
Доказательство.
если на этом же множестве выпукла
выпуклая и неубывающая, а функция
выпуклое, выпуклая на этом множестве.
определенная равенством
U.
Для любых
u, v ÎU , a Î [ 0,1]
I (u ) j ( g (u ) ) , u Î U ,
имеем
g
æ выпуклость
ö
£a g ( u ) + ( 1-a ) g ( v )
ç 6 4 4 7 4 4 8 ÷ монотонность j
£ j ( a g (u ) + (1 - a ) g (v) ) £
I au + ( 1- a ) v j ç g ( au + ( 1-a ) v) ÷
ç
÷
ç
÷
è
I (u )
I (v )
64 7 48
64 7 48 ø
(
)
выпуклость j
£
aj ( g ( u ) ) + (1 - a ) j ( g ( v ) )
Теорема доказана.
a I (u ) + (1 - a ) I (v).

16.

Следствие 1. Пусть функция
множестве
U Rn .
g : U ® [ a , b] выпукла и неотрицательна на выпуклом
Тогда функция
I : U ® R 1 , определенная равенством
I (u ) g p ( u ) , u Î U , p ³ 1
выпукла на множестве U .
Доказательство. Функция j ( g ) g , g ³ 0, p ³ 1 - является выпуклой и монотонной.
p
Следствие 2.
Пусть функция
g : U ® [ a , b]
U R n . Тогда функция I : U ® R 1 ,
(
I ( u ) max { 0, g ( u ) }
выпукла на множестве
U.
Доказательство. Функция g
на множестве
U,
+
выпукла на выпуклом множестве
определенная равенством
)
p
(g
+
( u) )
p
, u ÎU , p ³ 1
( u ) max { 0, g ( u ) } является выпуклой и положительной
если функция
g - выпуклая. Справедливость доказываемого
утверждения следует теперь из предыдущего следствия.