Similar presentations:
Выпуклый анализ. Теоремы об отделимости выпуклых множеств. Лекция 19
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 196. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХ
МНОЖЕСТВ (ПРОДОЛЖЕНИЕ)
2.
6. ТЕОРЕМЫ ОБ ОТДЕЛИМОСТИ ВЫПУКЛЫХМНОЖЕСТВ (ПРОДОЛЖЕНИЕ)
6.5. Теорема Фаркаша
3.
B ¸ m ´ n, B ¸ ( s - m ) ´ n, s ³ mn
причем множество X = x Î R Bx £ 0, Bx = 0 ¹ Æ.
n
Теорема 6 (Фаркаша). Для вектора v Î R неравенство v, x £ 0
6.5. Теорема Фаркаша Пусть заданы матрицы
{
выполняется для всех
вектора u Î R
m
xÎ X
}
в том и только том случае, если существуют
, u ³ 0, u Î R s - m ,
v = B ' u + B ' u (вектор v
B и B с положительными
такие что
является линейной комбинацией строк матриц
коэффициентами при строках матрицы
B).
Приведем эквивалентную формулировку теоремы. Полагаем
{
}
Y = y Î R n y = B ' u + B ' u , u Î R m , u ³ 0, u Î R s - m .
Y
Y-
выпуклый и замкнутый конус. Замкнутость множества
является следствием непрерывности линейных функций . Докажем его выпуклость.
Заметим, что множество
m
s -m
yi Î Y Þ yi = B ' ui + B ' ui , ui Î R , ui Î R , ui ³ 0, i = 1, 2
a Î [ 0, 1] . Тогда
Пусть
и
ya = a y1 + ( 1 - a ) y2 = a éë B ' u1 + B ' u1 ùû + ( 1 - a ) éë B ' u2 + B ' u2 ùû =
4.
= a éë B ' u1 + B ' u1 ùû + ( 1 - a ) éë B ' u2 + B ' u2 ùû =ua ³ 0,ÎR
ÎR
é 6 44
é 6 44ua 7
7 4 48 ù
4 48 ù
³0
ê
ú
ê
ú
= B ' a u1 + ( 1 - a ) u2 + B ' a u1 + ( 1 - a ) u2 = B ' ua + B ' ua Î Y .
ê
ú
ê
ú
êë
úû
êë
úû
s-m
m
Y - конус. Действительно, пусть l ³ 0 и
m
s -m
y
=
B
'
u
+
B
'
u
,
u
Î
R
,
u
³
0,
u
Î
R
.
y ÎY Þ
³ 0,ÎR m
Î}
R s -m
}
³ 0,ÎR
ÎR
l y = l B ' u + l B ' u = B ' lu + B ' lu Þ l y Î Y .
Покажем, что множество
Тогда
s -m
m
Эквивалентная формулировка теоремы.
v, x £ 0 "x Î X Û v Î Y .
x Î X справедливо
v Î Y . Предположим, что v Ï Y . Тогда по
Доказательство. Необходимость. Пусть v Î R
v, x £ 0.
Требуется доказать, что
теореме 2 существует вектор
l Î Rn , l ¹ 0
n
и для всех
такой, что
l , y > l , v , "y Î Y Þ
-l , y < -l , v , "y Î Y .
5.
-l , y < -l , v , "y Î Y . Обозначая c = -l ,c, y < c, v , "y Î Y .
{
}
( 1)
c Î X = x Î R n Bx £ 0, Bx = 0 .
Y - конус. Тогда l y Î Y "l ³ 0. Из (1)следует
Покажем, что
Множество
приходим к неравенству
}ÎY
³0
c, l y < c, v Þ l c, y < c, v , "y Î Y , "l ³ 0.
Неравенство (2) возможно для
"y Î Y , "l ³ 0
c, y £ 0. "y Î Y .
( 2)
только, если
( 3)
³0
m
s-m
в силу (3) выводим
y Î Y Û y = B ' u + B ' u и всех u Î R , u ³ 0, u Î R
B 'u + B 'u
}
0 ³ c, y
= c, B ' u + B ' u = c, B ' u + c, B ' u = Bc, u + Bc, u Þ
Для
Bc, u + Bc, uв проекции
£ 0 Þ ( на i ю координату
m
å ( Bc )
i =1
i
s-m
u + å ( Bc ) u j £ 0, "u i ³ 0, i = 1,L , m, "u j Î R1
i
j =1
j
)
( 4)
6.
ms-m
j
i
j
1
Покажем, что из (4) å ( Bc ) u + å ( Bc ) u £ 0, "u ³ 0, i = 1,L , m, "u Î R
i
i
i =1
j =1
следует
Bc £ 0, Bc = 0.
От противного приходим к
$i Î { 1,L , m} : ( Bc ) > 0
i
Тогда выбором
u >0
i
или
или
$j Î { 1,L , s - m} : ( Bc ) ¹ 0.
j
u Î ( -¥, +¥ ) , sign ( u
j
можно нарушить неравенство (4). Доказанные соотношения
{
}
j
) = sign ( ( Bc )
³0
c, l y < c, v Þ
c, l y
l =0
)
Однако
< c, v Þ c, v > 0.
Полученное противоречие доказывает необходимость
Достаточность. Пусть
{
j
Bc £ 0, Bc = 0
c Î X = x Î R n Bx £ 0, Bx = 0 .
По условиям необходимости должно выполняться c Î X Þ v, c £ 0.
в силу l y Î Y "l ³ 0 из (1) c, y < c, v , "y Î Y ( 1) следует
означают, что
( 4)
j
}
v Î Y = y Î R n y = B ' u + B ' u , u Î R m , u ³ 0, u Î R s - m .
7.
{v Î Y = y Î R n y = B ' u + B ' u , u Î R m , u ³ 0, u Î R s - m
Требуется доказать, что
{
}
}
v, x £ 0 "x Î X = x Î R n Bx £ 0, Bx = 0 .
Действительно,
³0
B ' u + B 'u
³0
xÎX
v , x = B ' u + B 'u , x =
}=0
}£0
u , Bx + u , Bx £ 0.
³0
Теорема доказана полностью.
Дадим геометрическую интерпретацию теореме Фаркаша для частного случая
s = m = 2, n = 2.
{
Тогда матрица
}
æ b11 b12 ö
B=ç
÷
b
b
è 21 22 ø
имеет размера
2´ 2
ì
ü
b11 b12 ö æ x1 ö
æ
ï
ï
2
X = x Î R Bx £ 0 = í x Î R ç
÷ × ç ÷ £ 0ý .
ï
ï
è b21 b22 ø è x2 ø
î
þ
æ b11 ö
æ b21 ö
Обозначим через b1 = ç
÷ , b2 = ç ÷ столбцы матрицы B. Тогда
è b12 ø
è b22 ø
n
и
8.
ìü
æ x1 ö
æ x1 ö
ï
ï
n
X = í x Î R b1 , ç ÷ £ 0, b2 , ç ÷ £ 0 ý ¹ Æ.
è x2 ø
è x2 ø
ï
ï
î
þ
Теорема 5 (Фаркаша).
выполняется для всех
B1
90
v B
2
Неравенство
900
что
v, x £ 0
в том и только том случае,
если существует вектор
0
X
xÎ X
æ v1 ö
2
Пусть v = ç ÷ Î R ,
è v2 ø
æ u1 ö 2
u = ç ÷ Î R , u1 ³ 0, u2 ³ 0,
è u2 ø
v = B ' u = b1u1 + b2u2 .
9.
Упражнение.Пусть
æ1ö
B2 = ç ÷
è 2ø
æ -2 ö
1
x( ) = ç ÷
è1ø
{
}
X = x Î R 2 Bx £ 0 .
æ 2ö
2. Доказать, что вектор
v=ç ÷
è 2ø
æ 2ö
v=ç ÷
è 2ø
v = u1 B1 + u2 B2
x
( 2)
æ1ö
=ç ÷
è -2 ø
v , x ( 2 ) = 2 × 1 + 2 × ( -2 ) < 0
B2
v
выполнено u1
³ 0, u2 ³ 0.
Решение.
ìïæ x ö
ü
2 y + 2 x £ 0, ï
X = íç ÷ Î R
ý,
2 y + x £ 0 ïþ
ïîè y ø
v, x ( 1) = 2 × ( -2 ) + 2 ×1 < 0
B1
1. Построить множество
æ 2 ö удовлетворяет условию v, x £ 0, x Î X .
B1 = ç ÷
è1ø
3. Показать. что в разложении
X
æx ö
x=ç 1÷
è x2 ø
æ2 1ö
B=ç
÷.
è1 2ø
Þ
v, x £ 0, x Î X .
2
2
æ 2ö
æ 1 ö æ 2 ö ì2u1 + u2 = 2
u1 × ç ÷+ u2 × ç ÷ = ç ÷ Þ í
Þ u1 = , u2 = Þ u1 > 0, u2 > 0.
3
3
è1ø
è 2 ø è 2 ø îu1 + 2u2 = 2




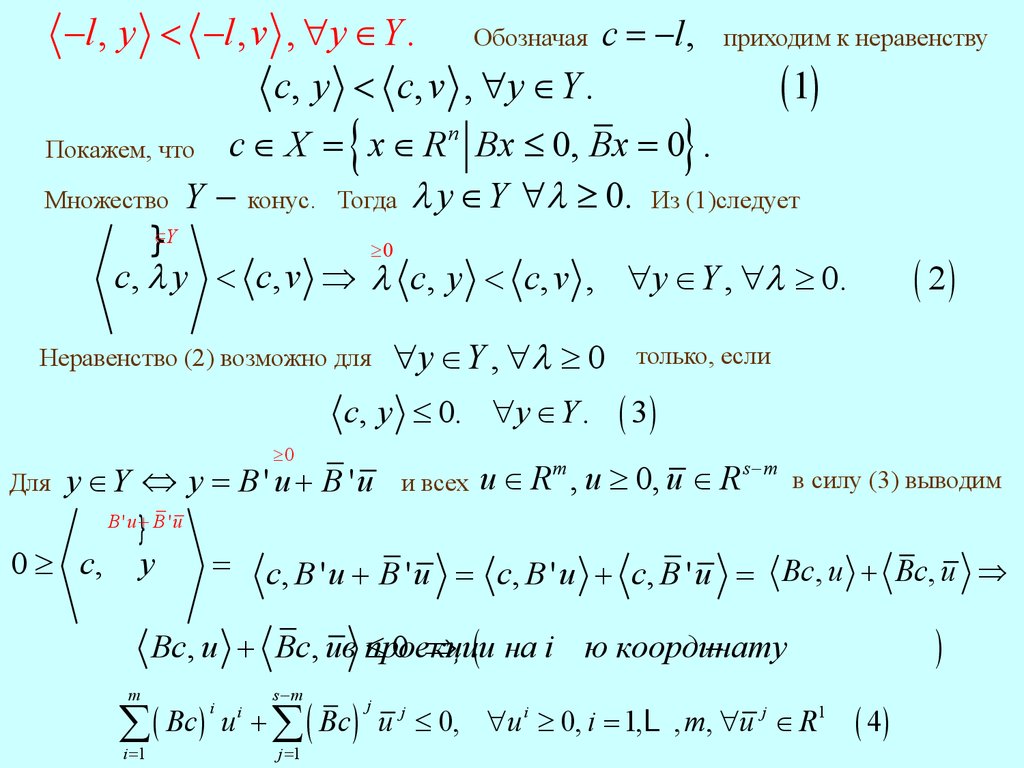






 mathematics
mathematics programming
programming








