ЗЛП и Word

1.

ЗЛП и Word
Доцент каф. ВМ и М, к.т.н. Каменских А.А.

2.

Задачи линейного программирования
(оптимизация)
Задачей линейного программирования (ЗЛП) называется задача отыскания
экстремума (максимума или минимума) линейной функции от нескольких
переменных при линейных ограничениях на эти переменные.
Найти максимальное значение целевой функции
F ( x1; x 2 ) = 2 x1 + 5 x 2 ® max
при следующих ограничениях
ì x1 + x 2 £ 127,
ï
í7 x1 - x2 £ 83,
ï x ³ 0, x ³ 0.
2
î 1
x1 , x 2
– система ограничений
– параметры оптимизации

3.

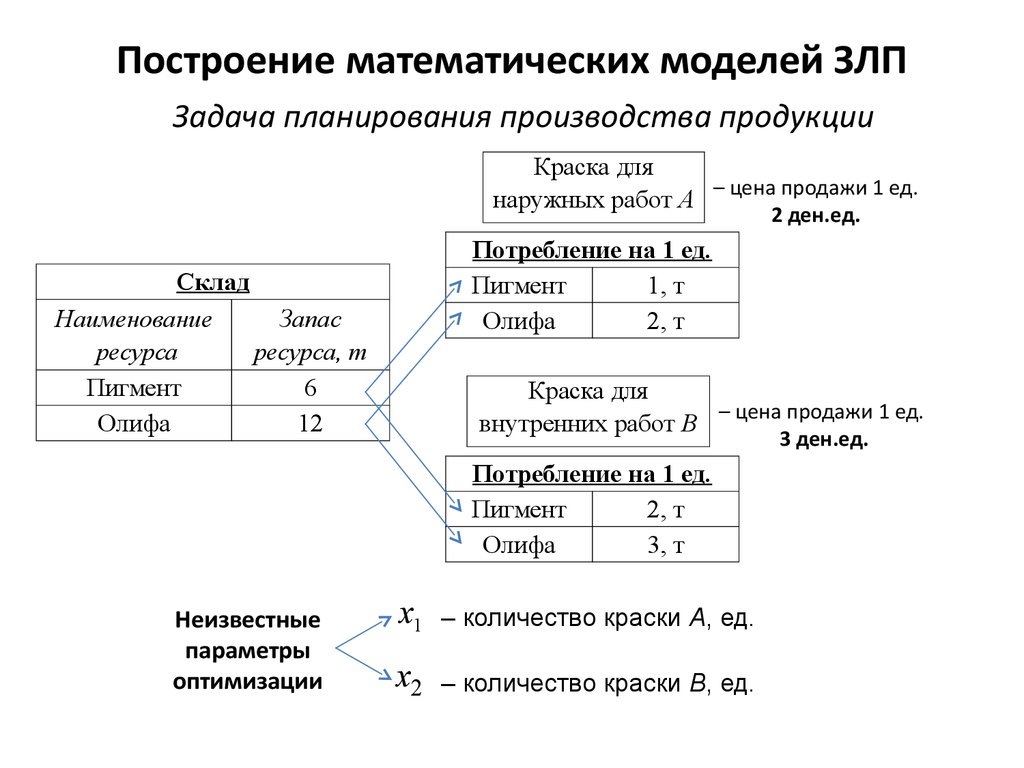
4. Построение математических моделей ЗЛП

Задача планирования производства продукции
Краска для
– цена продажи 1 ед.
наружных работ А
2 ден.ед.
Потребление на 1 ед.
Пигмент
1, т
Олифа
2, т
Склад
Наименование
Запас
ресурса
ресурса, т
Пигмент
6
Олифа
12
Краска для
– цена продажи 1 ед.
внутренних работ B
3 ден.ед.
Потребление на 1 ед.
Пигмент
2, т
Олифа
3, т
Неизвестные
параметры
оптимизации
x1
– количество краски А, ед.
x2
– количество краски B, ед.

5. Математическая модель

Суммарная прибыль фирмы от продажи краски:
F ( X ) = F ( x1; x 2 ) = 2 x1 + 3x 2 ® max
– целевая функция
Ограничения будут двух сортов. Первый – это не превышение расхода
исходных продуктов для изготовления краски их суточных запасов. Второй – это
не превышение продажи краски для наружных работ А ее суточного спроса.
Кроме указанных ограничений должно в обязательном порядке (и это
определяется постановкой самой экономической задачи) должно выполняться
условие неотрицательности производства краски. Итак, получаем полную
систему ограничений для нашей задачи:
Система ограничений
ì x1 + 2 x 2 £ 6,
ï2 x + 3 x £ 12,
ï 1
2
í
ï x1 £ 4,
ïî x1 ³, x2 ³ 0.
– ограничение по запасам Пигмента
– ограничение по запасам Олифы
– ограничение по производству краски А
– нельзя производить отрицательное кол-во краски

6.

Задача о составлении оптимального рациона
Требуется в сутки
Наименование
Не менее чем
Кормовые ед.
Перевариваемый протеин
16,1 кг.
1816 г.
Содержание питательных веществ в 1 кг корма и себестоимость кормов
Показатель
Комбикорм
Сено
Силос
Кормовые единицы, кг
Переваримый протеин, г
1
160
0,5
60
0,2
30
Себестоимость 1 кг корма, руб.
4,2
0,9
0,6
Согласно физиологическим особенностям животных в рационе должно
содержаться не менее 31% комбикормов и не более 26% сена от общей
потребности в кормовых единицах.

7. Математическая модель

.
Математическая модель
Целевая функция – общая стоимость суточного рациона кормления:
F ( X ) = 4, 2 x1 + 0,9 x 2 + 0, 6 x3 ® min
Составим систему ограничений:
1) условие по содержанию кормовых единиц в рационе:
x1 + 0,5 x 2 + 0, 2 x3 ³ 16,1
2) условие по содержанию перевариваемого протеина в рационе:
160 x1 + 60 x2 + 30 x3 ³ 1819
3) условие по содержанию комбикорма в рационе (не менее 31%) :
x1 ³ 4,991
4) условие по содержанию сена в рационе (не более 26%)
0,5 x2 £ 4,186
5) условие неотрицательности количества корма каждого вида:
x1 ³ 0, x 2 ³ 0, x3 ³ 0

8.

Пример решения в MS EXCEL
Постановка задачи
Расход сырья на изготовление одного
изделия
Используемое сырьё
1 типа
Доски, м
2
Обивочная ткань, м
0,5
Рабочее время, чел./час
2
Стоимость,
80
x1 – числоруб.
изготовленных стульев
2 типа
x2
Кол-во сырья в
распоряжении
фабрики
4
440
0,25
65
2,5
320
120
max
– число
изготовленных кресел
F ( X ) = 80 x1 + 120 x2 ® max – целевая функция прибыли
Система ограничений
ì2 x1 + 4 x2 £ 440,
ì2 x1 + 4 x2 £ 440,
ï0,5 x + 0, 25 x £ 65,
ï0,5 x + 0, 25 x £ 65,
ï
ï
1
2
1
2
Ûí
í
ï2 x1 + 2,5 x2 £ 320,
ï2 x1 + 2,5 x2 £ 320,
ïî x1 ³ 0, x2 ³ 0,
ïî- x1 £ 0,
- x2 £ 0.

9.

Пример решения задачи в MS EXCEL
СУММПРОИЗВ(B4:С4; $B$10:$С$10)
СУММПРОИЗВ(B7:С7; B10:С10)
Использование Надстройки «Поиск решения»

10.

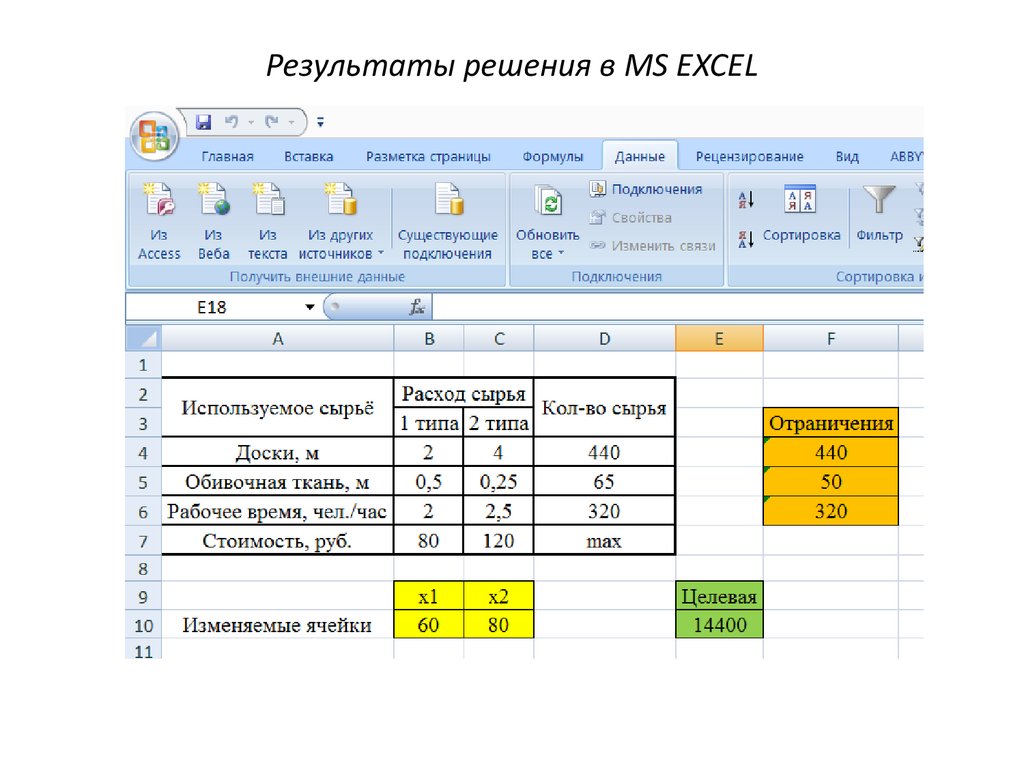
Результаты решения в MS EXCEL

11.

Транспортная задача
Транспортная задача — математическая задача линейного программирования
специального вида о поиске оптимального распределения однородных объектов от
поставщика к потребителю с минимизацией затрат на перемещение.
Цель – минимизация суммарных расходов на все перевозки

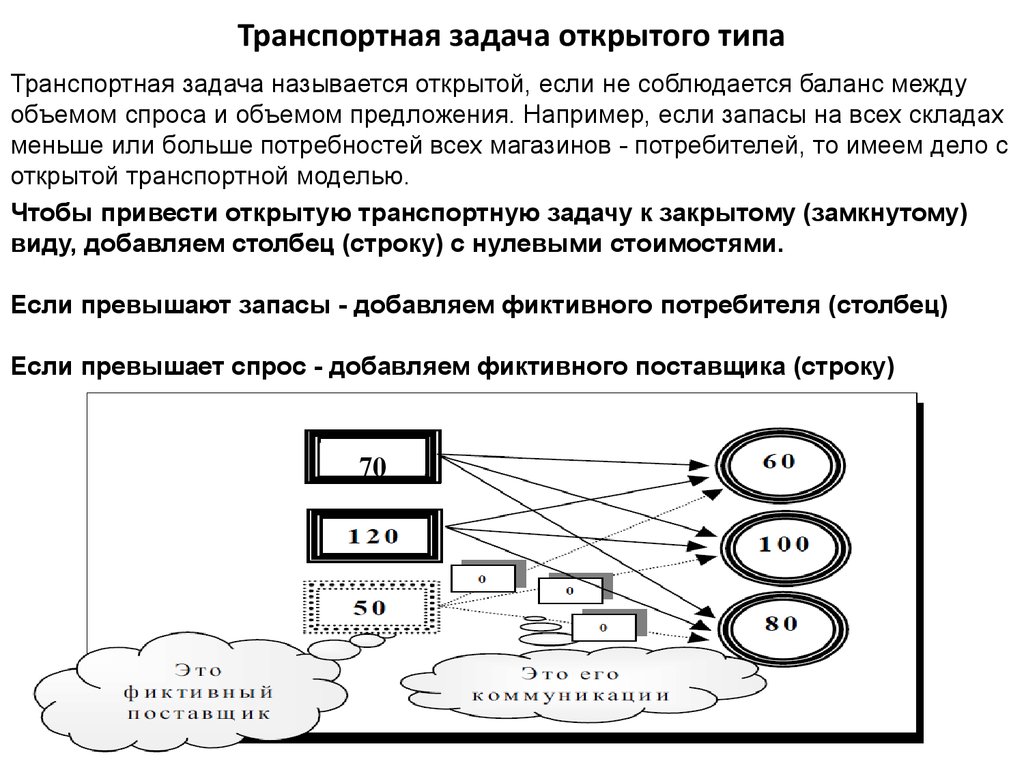
12. Транспортная задача открытого типа

Транспортная задача называется открытой, если не соблюдается баланс между
объемом спроса и объемом предложения. Например, если запасы на всех складах
меньше или больше потребностей всех магазинов - потребителей, то имеем дело с
открытой транспортной моделью.
Чтобы привести открытую транспортную задачу к закрытому (замкнутому)
виду, добавляем столбец (строку) с нулевыми стоимостями.
Если превышают запасы - добавляем фиктивного потребителя (столбец)
Если превышает спрос - добавляем фиктивного поставщика (строку)
70

13. Математическая модель

xij
– количество перевозимой продукции от поставщика номер i к потребителю номер j
X = ( x11 , x12 , x13 , x 21 , x 22 , x 23 , x31 , x32 , x33 )
Целевая функция – общая стоимость всех перевозок:
F ( X ) = 5 x11 + 10 x12 + 12 x13 + 8 x 21 + 6 x 22 + 4 x 23 + 0 x31 + 0 x32 + 0 x33 ® min
Общий вид целевой функции
m
n
F ( X ) = åå cij xij ® min
i =1 j =1
cij
– элементы матрица стоимостей перевозок
é5
ê
C = ê8
ê
êë0
10
6
0
12 ù
ú
4ú
ú
0 úû

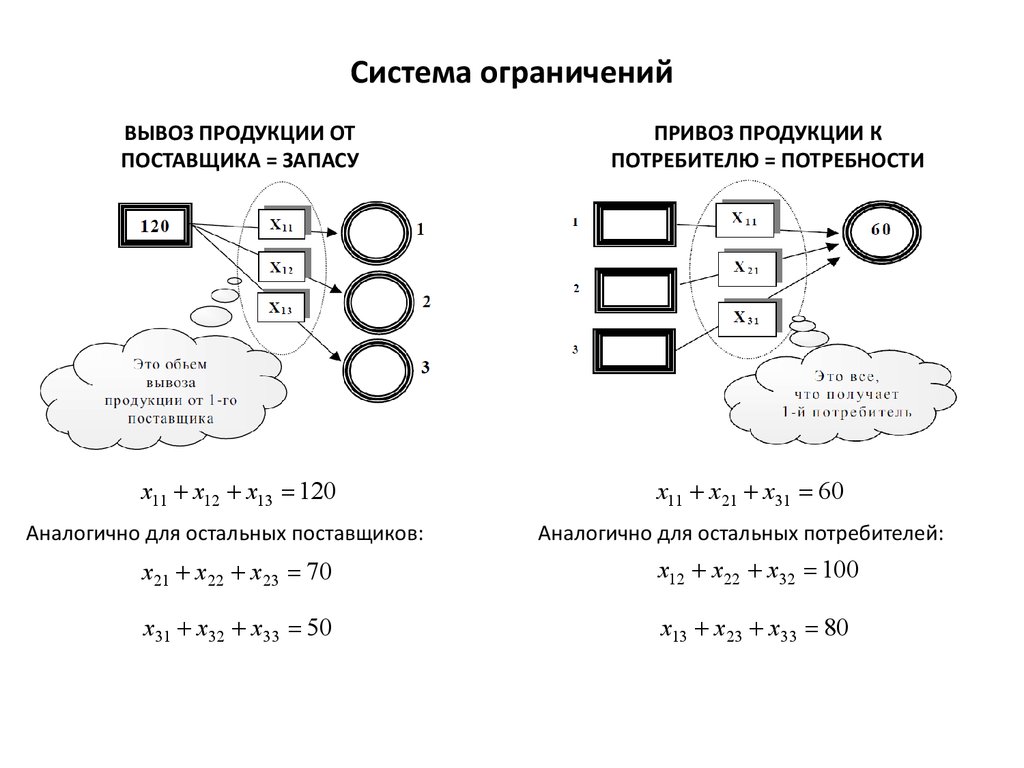
14. Система ограничений

ВЫВОЗ ПРОДУКЦИИ ОТ
ПОСТАВЩИКА = ЗАПАСУ
x11 + x12 + x13 = 120
Аналогично для остальных поставщиков:
ПРИВОЗ ПРОДУКЦИИ К
ПОТРЕБИТЕЛЮ = ПОТРЕБНОСТИ
x11 + x21 + x31 = 60
Аналогично для остальных потребителей:
x 21 + x 22 + x 23 = 70
x12 + x22 + x32 = 100
x31 + x32 + x33 = 50
x13 + x 23 + x33 = 80

15.

Пример решения транспортной задачи в MS EXCEL
В хозяйстве за время уборки при заготовке силоса необходимо перевезти 3000т
зелёной массы с четырех полей к четырём фермам, в том числе с первого поля 1000т,
второго – 600т, третьего – 800т, четвёртого – 600т. Для первой фермы требуется 600т
зелёной массы, второй – 800т, третьей – 1000т и четвертой – 1000т. Стоимость перевозки
1 т зелёной массы с полей к фермам приведена в таблице ниже. Требуется составить такой
план перевозки массы, чтобы транспортные затраты были минимальны.
Пункты назначения (фермы)
Пункты
отправления
(поля)
B1
B2
B3
B4
A1
A2
A3
A4
Заявки bj, т
3
5
7
5
600
6
4
1
2
800
5
4
5
3
1000
1
6
4
5
1000
Запасы
ai, т
1000
600
800
600

16.

СУММПРОИЗВ(B3:E6;J3:M6)
СУММ(J3:J6)
!!!Запас меньше потребности!!!
СУММ(J3:M3)

17.

СУММПРОИЗВ(B3:E7;J3:M7)
СУММ(J3:J7)
СУММ(J3:M3)