Функции. Предел функции. Лекция1

1. Функции. Предел функции

2. Понятие функции

Функция – это соответствие между множествами X и Y,
при котором каждому элементу множества X ставится в
соответствие единственный элемент множества Y.
y f ( x), где x X , y Y
y – зависимая переменная (функция),
x – независимая переменная (аргумент).

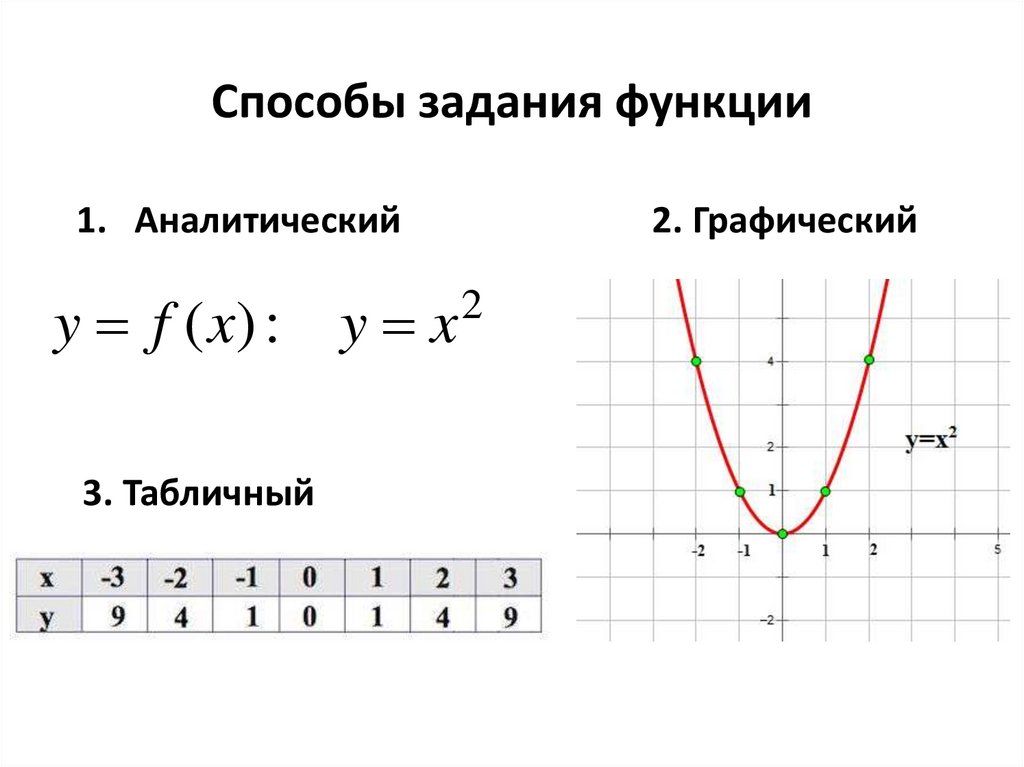
3. Способы задания функции

1. Аналитический
y f ( x) : y x
3. Табличный
2. Графический
2

4. Основные свойства функций

1) Область определения. Множество
значений аргумента, при которых функция
имеет смысл. x D
2) Область значений. Множество значений,
которые принимает сама функция. y E
3) Ограниченность. Функция y=f(x) называется
ограниченной, если существует такое число
M, что для всех x из области определения
справедливо: f ( x) M

5. Основные свойства функций

4) Монотонность. Возрастание или убывание функции.
Функция называется возрастающей, если для пары
значений x1 x2 справедливо неравенство: f ( x1 ) f ( x2 )
Функция называется убывающей, если для пары
значений x1 x2 справедливо неравенство: f ( x1 ) f ( x2 )
5) Четность. Функция называется четной, если для любого
x D справедливо равенство: f ( x) f ( x)
Функция называется нечетной, если для любого x D
справедливо равенство: f ( x) f ( x)

6. Основные свойства функций

6) Периодичность. Функция называется периодичной с
периодом T 0 , если для любого x D выполняется
равенство: f ( x T ) f ( x) f ( x T )
7) Нули функции. Значения аргумента, при которых
функция равна нулю. f ( x) 0
8) Экстремумы функции. Значения аргумента, при
которых функция принимает
f ( x) max
максимальные/минимальные значения. f ( x) min

7. Предел функции

Пусть функция f(x) определена на некотором открытом
интервале X, содержащем точку x=a.
Число L называется пределом функции f(x) при x a ,
если для каждого 0 существует такое число 0 , что:
f ( x) L при условии 0 x a
Обозначение:
lim f ( x) L
x a

8. Свойства пределов

1) Предел суммы функций равен сумме пределов:
lim f ( x) g ( x) lim f ( x) lim g ( x)
x a
x a
x a
2) Предел постоянной величины равен самой
постоянной величине: lim C C
x a
3) Предел произведения функции на постоянную
величину. Постоянный множитель можно
выносить за знак предела:
lim Cf ( x) C lim f ( x)
x a
x a

9. Свойства пределов

4) Предел произведения функций равен
произведению пределов:
lim f ( x) g ( x) lim f ( x) lim g ( x)
x a
x a
x a
5) Предел частного от двух функций равен отношению
пределов при условии, что предел знаменателя не
равен нулю:
lim
f
(
x
)
f ( x ) x a
lim
, при lim g ( x) 0
x a g ( x )
x a
lim g ( x)
x a

10. Свойства пределов

6) Предел степенной функции:
lim f ( x) lim f ( x)
x a
x a
p
p
7) Предел показательной функции:
lim A
x a
f ( x)
A
lim f ( x )
x a
, где A 0
8) Предел логарифмической функции:
lim log A f ( x) log A lim f ( x), где A 0
x a
x a