День победы. Точные науки в годы ВОВ

1. Урок- праздник День Победы

Точные науки в годы ВОВ
Учитель: Хазина Н.П.

2. Вставай, страна огромная!»

• Через два дня после начала войны, 24 июны 1941 года,
одновременно в газетах «Известия» и «Красная звезда»
были опубликованы стихи поэта В.И. Лебедева-Кумача
«Священная война». Сразу же после публикации
композитор А.В. Александров написал к ним музыку.
• Песня приобрела массовую популярность на фронтах
Великой Отечественной войны и поддерживала
высокий боевой дух в войсках, особенно в тяжёлых
оборонительных боях.

3. Важнейшие сражения Советской армии в годы Великой отечественной войны

Прибалтийская военная операция (22 июня - 9 июля 1941)
Смоленское сражение (10 июля-10 сентября 1941)
Битва за Ленинград (10 июля 1941- 9 августа 1944)
Битва за Москву (30 сентября 1941- 7 января 1942)
Ржевско-Вяземская операция (8 января-20 апреля 1942)
Сталинградская битва (17 июля 1942-2 февраля 1943 года)
Битва за Кавказ (25 июля 1942-9 октября 1943)
Курская битва (5 июля-23 августа 1943)
Витебская операция (3 февраля -13 марта 1944)
Белорусская операция (23 июня-29 августа 1944)
Висло-Одерская операция (12 января-3 февраля 1945)
Битва за Берлин (16 апреля-8 мая 1945)

4. Солдатский треугольник

• Жди меня, и я вернусь.
Только очень жди,
Жди, когда наводят грусть
Желтые дожди,
Жди, когда снега метут,
Жди, когда жара,
Жди, когда других не ждут,
Позабыв вчера.
Жди, когда из дальних мест
Писем не придет,
Жди, когда уж надоест
Всем, кто вместе ждет.

5. Математика для боевых операций

• В годы Великой Отечественной войны
подготовка боевых операций, а их было много,
была сопряжена с огромным количеством
расчетов, которые требовали хороших знаний по
математике.

6. Определение высоты предмета с помощью длинного шеста

• Вот так однажды на одном из
фронтов Великой Отечественной
войны разведывательная группа во
главе с сержантом Поповым,
получила задание измерить высоту
деревьев для постройки моста через
горную реку, на противоположном
берегу которой засели фашисты.
• Высоту деревьев сержант определял
с помощью вешки так, как это
показано на рисунке. Эпизод был
описан в журнале «Военные
знания» №8,1949 г. в статье А.
Демидова «Разведка реки».

7. Задача на измерение ширины реки с помощью козырька

• Этот способ пригодился
старшему сержанту Куприянову
во фронтовой обстановке. Его
отделение получило задание
измерить ширину реки, через
которую предстояло
организовать переправу.
• На рисунке показано, как можно определить ширину реки,
рассматривая два равных треугольника. Надо стать лицом к
реке и надвинуть фуражку на глаза так, чтобы нижний
обрез козырька точно совпал с линией противоположного
берега. Затем, не изменяя положения головы, надо
повернутся налево, и заметить самую длинную точку,
видимую из-под козырька.

8. Теория вероятности артиллеристам

• Академик А. Н. Колмогоров по заданию Главного
артиллерийского управления, используя свои работы по
математике в области теории вероятностей, дал
определение
наиболее
выгодного
рассеяния
артиллерийских снарядов и рассчитал количество
одновременных выстрелов по самолету противника, для
того, чтобы иметь наибольшую вероятность сбить
самолет противника. Он определил наилучшие методы
нахождения самолетов и подводных лодок противника,
позволяющие избежать встречи с подлодками врага.

9. Вероятность уничтожения цели

• Задача из ЕГЭ: При артиллерийской стрельбе автоматическая
система делает выстрел по цели. Если цель не уничтожена, то
система делает повторный выстрел. Выстрелы повторяются до
тех пор, пока цель не будет уничтожена. Вероятность
уничтожения некоторой цели при первом выстреле равна 0,4, а
при каждом последующем - 0,6. Сколько выстрелов потребуется
для того, чтобы вероятность уничтожения цели была не менее
0,98?
• Решение: Можно решать задачу «по действиям», вычисляя
вероятность уцелеть после ряда последовательных промахов:
Р(1) = 0,6.
Р(2) = Р(1)·0,4 = 0,24.
Р(3) = Р(2)·0,4 = 0,096.
Р(4) = Р(3)·0,4 = 0,0384;
Р(5) = Р(4)·0,4 = 0,01536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти
выстрелов по мишени.

10. Математика артиллеристам

• Член-корреспондент АН СССР Н.Г. Четаев во
время войны с помощью математических вычислений
рассчитал наиболее выгодную крутизну нарезки
стволов орудий, что позволило обеспечить кучность
боя и устойчивость снарядов при полете.

11. Вклад ученых-физиков

L
Вклад ученых-физиков
• 3адача: Окоп противника на расстоянии 1 км виден
под углом 0,17 артиллерийских единиц (а.е.). Какова
его длина?
• В артиллерии для измерения углов используется своя
система. Круг делится на 60 а.е., т.е. 3600 = 60 а.е., 60 = 1 а.е.;
0,01 а.е. называется малой единицей. Поэтому угол
обозначается так: 3-10 (3 большие единицы и 10 малых). Эту
величину легко перевести в градусы:
3-10 это 3,10 а.е., 3,10 • 60 = 18,60.
Решение задачи:
• 0,17 а.е.=0,17* 60 ≈10
• tg 10 = 0,017
• L = 1000• 0,017=17 (м)

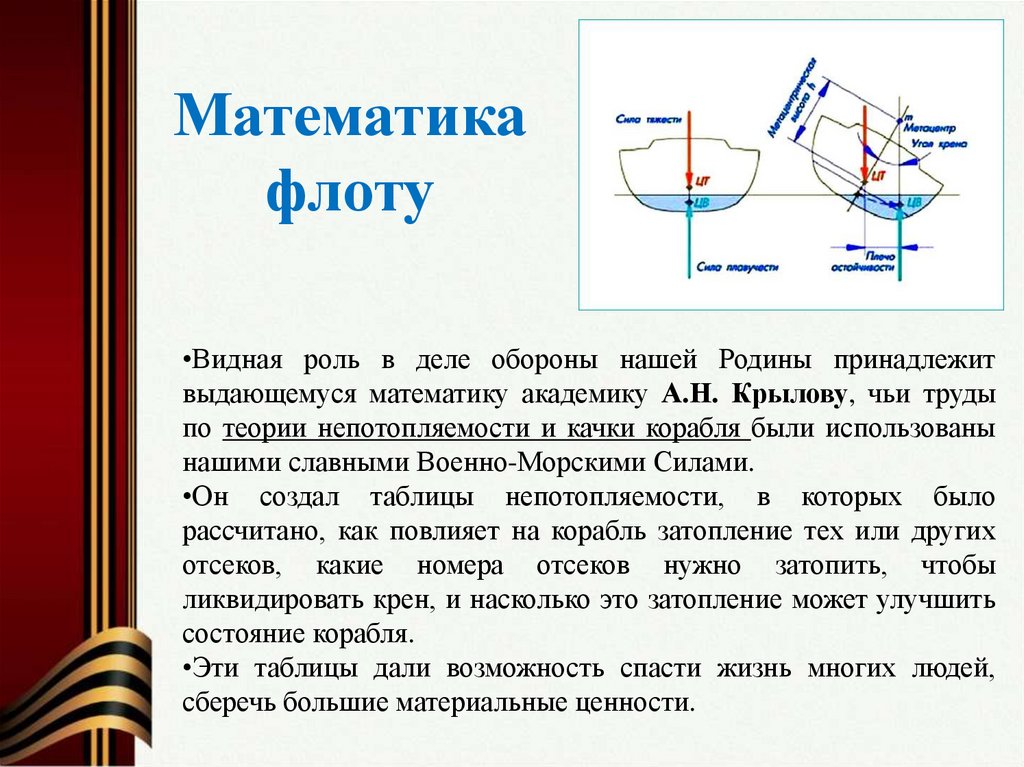
12. Математика флоту

•Видная роль в деле обороны нашей Родины принадлежит
выдающемуся математику академику А.Н. Крылову, чьи труды
по теории непотопляемости и качки корабля были использованы
нашими славными Военно-Морскими Силами.
•Он создал таблицы непотопляемости, в которых было
рассчитано, как повлияет на корабль затопление тех или других
отсеков, какие номера отсеков нужно затопить, чтобы
ликвидировать крен, и насколько это затопление может улучшить
состояние корабля.
•Эти таблицы дали возможность спасти жизнь многих людей,
сберечь большие материальные ценности.

13. Корабль - разведчик

• Задача 4. Разведывательному
кораблю
(разведчику),
двигавшемуся
в
составе
эскадры,
дано
задание
обследовать район моря на 70
миль в направлении движения
эскадры. Скорость эскадры - 35
миль
в
час,
скорость
разведчика - 70 миль в час.
Определить, через сколько
времени разведчик возвратится
к эскадре.
• На
рисунке
крейсер
Черноморского флота под
огнем фашистских береговых
батарей 1942год.

14. Решение задачи

15. Вклад ученых-химиков

Сплав меди и цинка получается латунь – хорошо
обрабатывается давлением и имеет высокую вязкость.
Использовался для изготовления гильз, патронов и
артиллерийских снарядов, так как обладает хорошим
сопротивлением ударным нагрузкам, создаваемым
пороховыми газами.
Задача из ЕГЭ. Кусок
латуни содержит цинка на 80
кг меньше, чем меди. Этот
кусок латуни сплавили со
120 кг меди и получили
латунь, в которой 75% меди.
Определите массу (в кг.)
первоначального
куска
латуни.

16. Решение задачи

Первый
сплав
Цинк
Медь
Латунь
х кг
(х+80) кг
х+(х+80)
=2х+80 – кг
Добавили
Второй
сплав
120 кг
х кг это 25%
сплава
25%=0,25
(х+80 + 120) кг 2х+80 + 120 =
это 75%
(2х+200) кг
сплава
Решение х=(2х+200)*0,25
уравнения х=100
Ответ:
100 кг - цинка
100 + 80 = 180 100+180=
(кг) – меди.
=280 (кг )
– первый
кусок латуни.

17. Математики для авиации

• Война требовала от авиации больших скоростей самолетов. При
освоении больших скоростей авиация столкнулась с внезапным
разрушением самолетов из-за вибрации особого рода – флаттера.
• Группа ученых математиков во главе с М.В. Келдышем
разработала сложную математическую теорию флаттера,
которая обеспечила самолеты надежной защитой от появления
вибраций, и позволила увеличить темпы выпуска боевых
самолетов.

18. Математика авиации

• Математический институт Академии наук СССР
разрабатывает штурманские таблицы, которые уже в 1943 г.
находят широкое применение в боевой практике авиации
дальнего действия. для расчета всех дальних полетов и
повышения точности самолетовождения.

19. Парашют

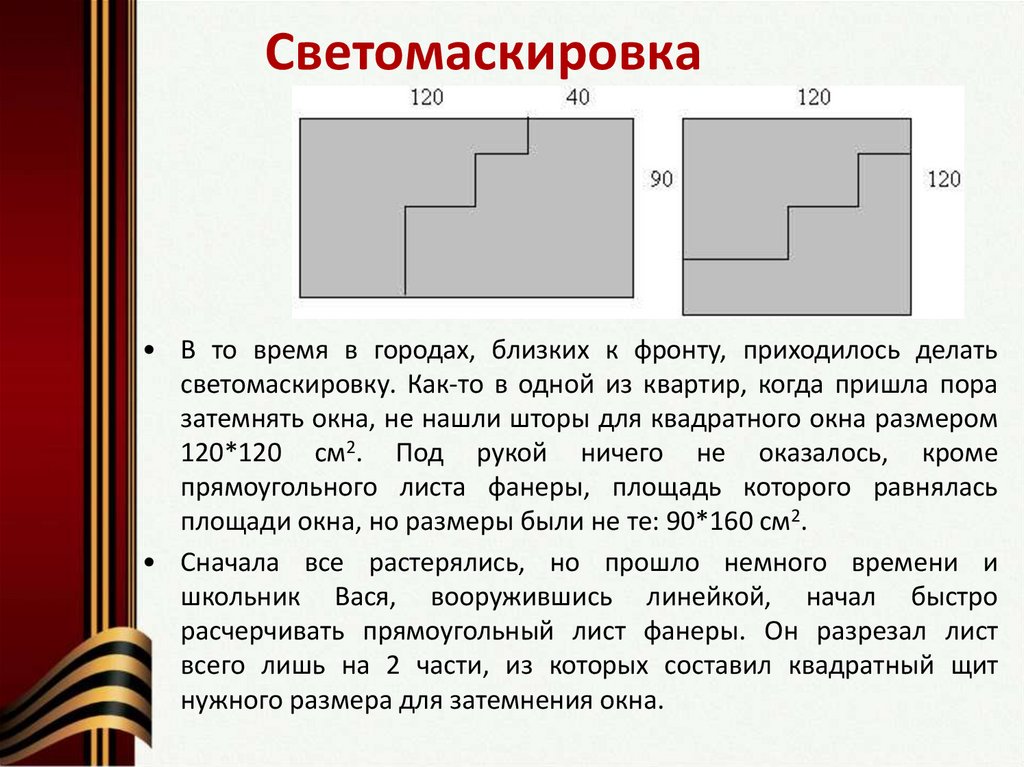
20. Светомаскировка

• В то время в городах, близких к фронту, приходилось делать
светомаскировку. Как-то в одной из квартир, когда пришла пора
затемнять окна, не нашли шторы для квадратного окна размером
120*120 см2. Под рукой ничего не оказалось, кроме
прямоугольного листа фанеры, площадь которого равнялась
площади окна, но размеры были не те: 90*160 см2.
• Сначала все растерялись, но прошло немного времени и
школьник Вася, вооружившись линейкой, начал быстро
расчерчивать прямоугольный лист фанеры. Он разрезал лист
всего лишь на 2 части, из которых составил квадратный щит
нужного размера для затемнения окна.

21. Минута молчания

Неугасима память поколений
И память тех, кого так свято чтим,
Давайте, люди, встаньте на мгновенье
И в скорби постоим и помолчим.
• Свыше 20 млн. человек потеряла наша страна в
Великой Отечественной войне. Если бы мы
посвятили каждой жертве по одной минуте молчания,
то сколько времени нам бы пришлось молчать?

22. Тяжело в учении, легко в бою /А.В. Суворов/

В современной российской
армии не только командиру,
но и солдату, чтобы
успешно справляться со
своими
обязанностями,
нужно владеть основами
электротехники,
радиотехники и хорошо
знать
математику
и
информатику.

23. Майский марафон. История ВОВ

Пройдите по ссылке и
выполните тест.
https://edu.skysmart.ru/student/h
amolobiko