Similar presentations:
Описанная окружность. 8 класс
1. Описанная окружность
Геометрия, 8 класс2.
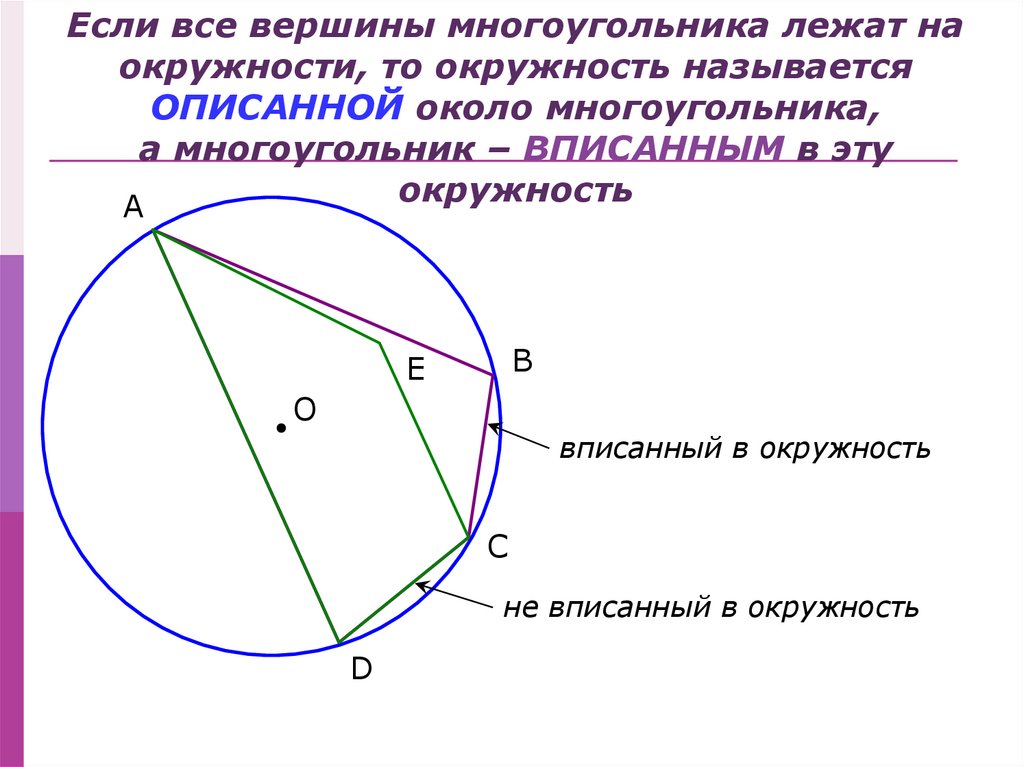
Если все вершины многоугольника лежат наокружности, то окружность называется
ОПИСАННОЙ около многоугольника,
а многоугольник – ВПИСАННЫМ в эту
окружность
A
B
E
O
вписанный в окружность
C
не вписанный в окружность
D
3.
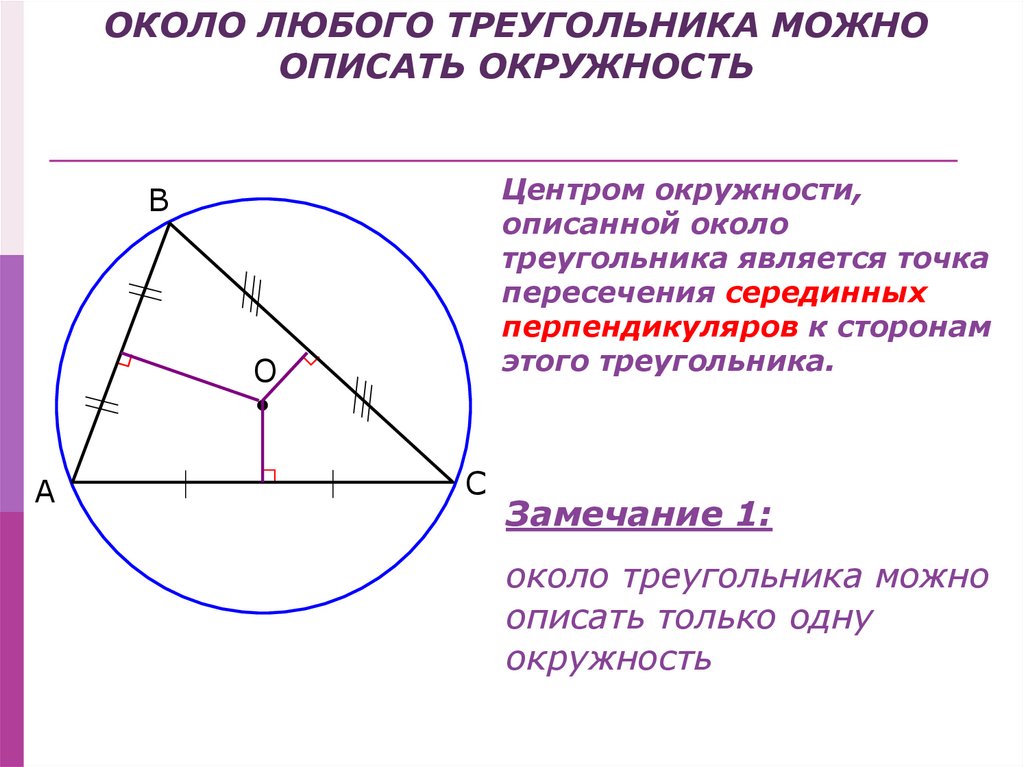
ОКОЛО ЛЮБОГО ТРЕУГОЛЬНИКА МОЖНООПИСАТЬ ОКРУЖНОСТЬ
Центром окружности,
описанной около
треугольника является точка
пересечения серединных
перпендикуляров к сторонам
этого треугольника.
В
О
А
С
Замечание 1:
около треугольника можно
описать только одну
окружность
4.
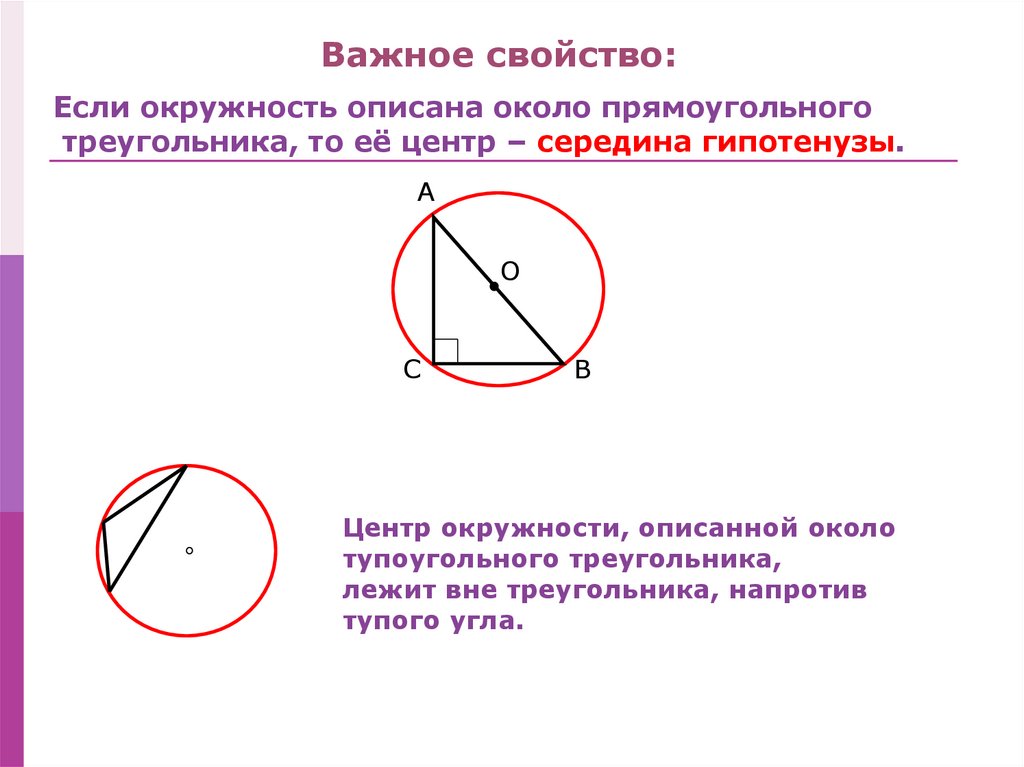
Важное свойство:Если окружность описана около прямоугольного
треугольника, то её центр – середина гипотенузы.
A
O
C
B
Центр окружности, описанной около
тупоугольного треугольника,
лежит вне треугольника, напротив
тупого угла.
5.
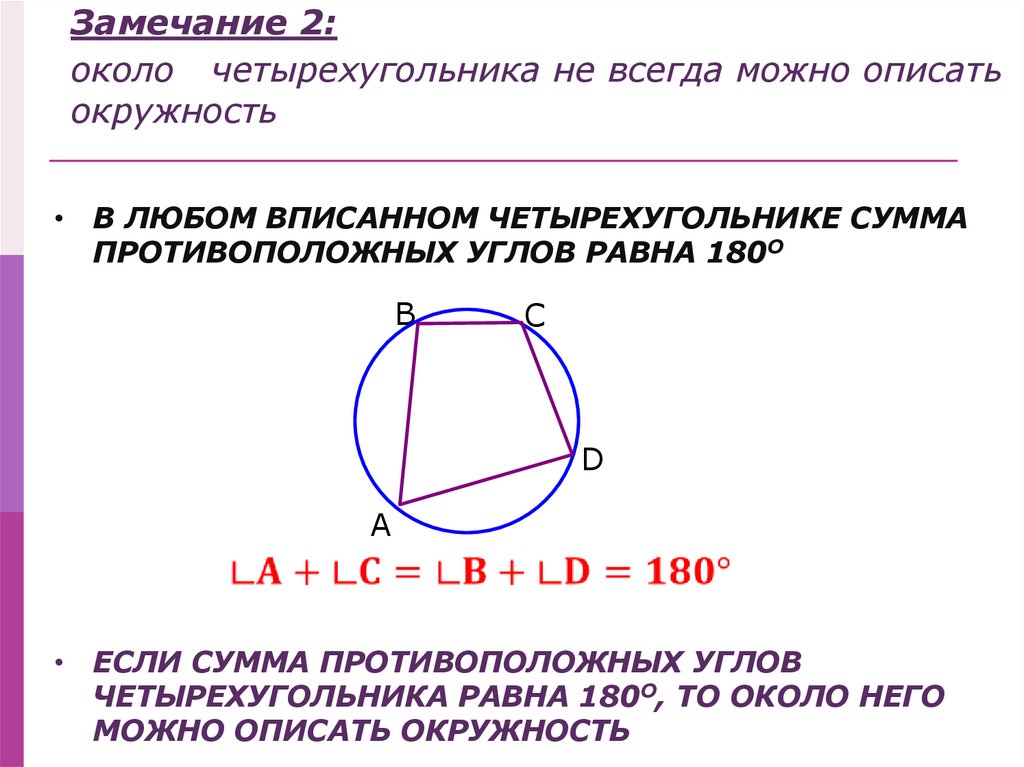
Замечание 2:около четырехугольника не всегда можно описать
окружность
• В ЛЮБОМ ВПИСАННОМ ЧЕТЫРЕХУГОЛЬНИКЕ СУММА
ПРОТИВОПОЛОЖНЫХ УГЛОВ РАВНА 180О
B
C
D
A
• ЕСЛИ СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ
ЧЕТЫРЕХУГОЛЬНИКА РАВНА 180О, ТО ОКОЛО НЕГО
МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ
6.
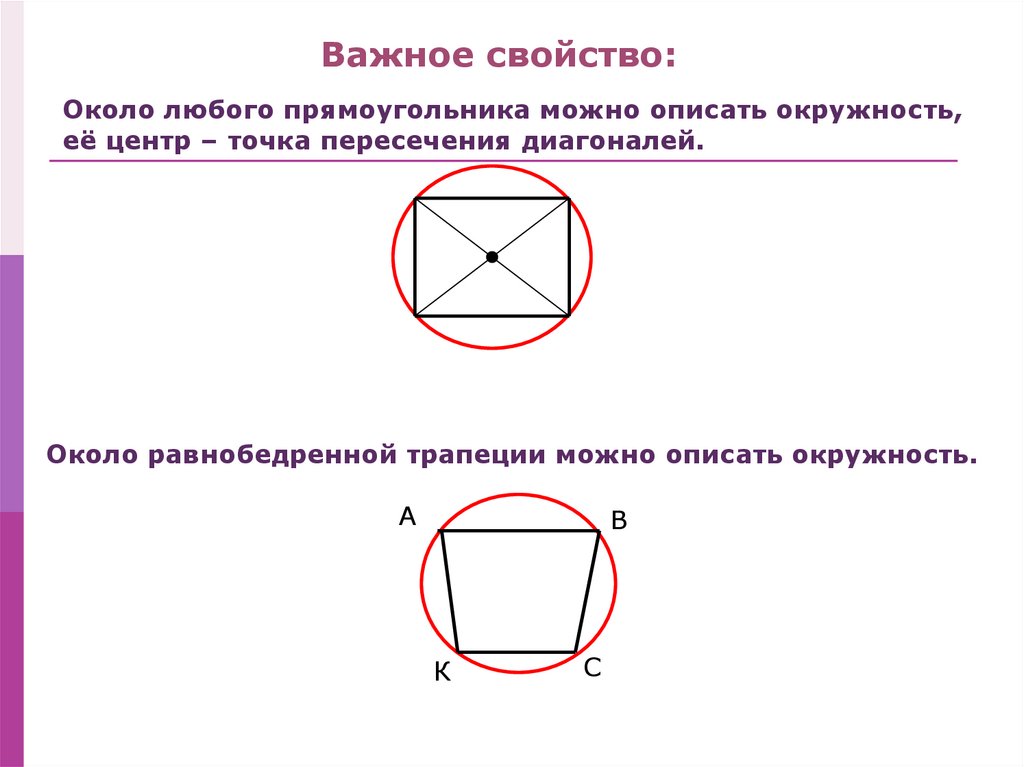
Важное свойство:Около любого прямоугольника можно описать окружность,
её центр – точка пересечения диагоналей.
Около равнобедренной трапеции можно описать окружность.
А
В
К
С
7.
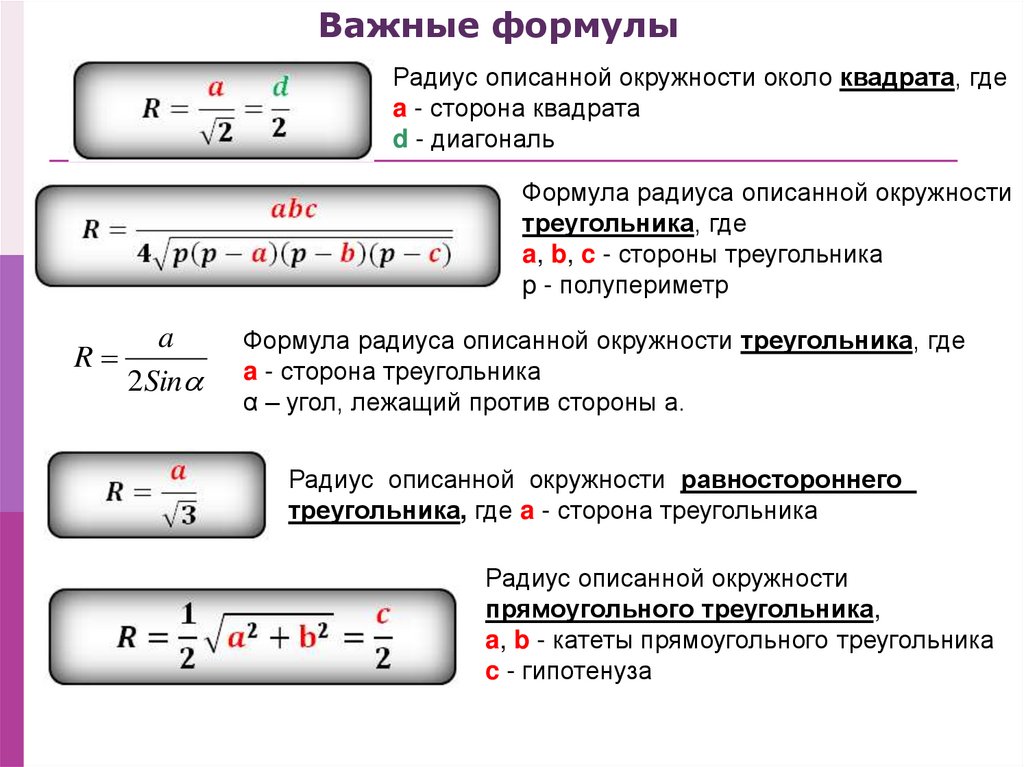
Важные формулыРадиус описанной окружности около квадрата, где
a - сторона квадрата
d - диагональ
Формула радиуса описанной окружности
треугольника, где
a, b, c - стороны треугольника
p - полупериметр
R
a
b
c
Формула
радиуса
описанной окружности треугольника, где
a - сторона
треугольника
2Sin 2Sin 2Sin
α – угол, лежащий против стороны а.
Радиус описанной окружности равностороннего
треугольника, где a - сторона треугольника
Радиус описанной окружности
прямоугольного треугольника,
a, b - катеты прямоугольного треугольника
c - гипотенуза

 mathematics
mathematics








