Similar presentations:
Описанная окружность. 8 класс
1. Тема: Описанная окружность
21 апреляКлассная работа
2.
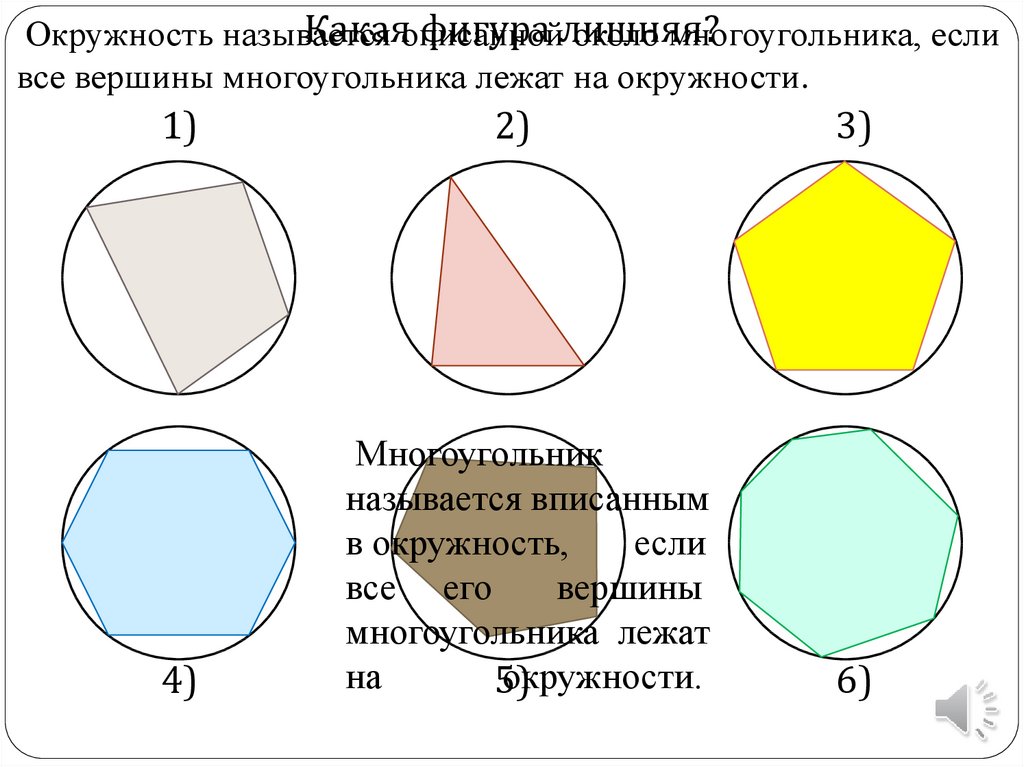
Какаяописаннойфигура лишняя?
Окружность называется
около многоугольника, если
все вершины многоугольника лежат на окружности.
1)
4)
2)
Многоугольник
называется вписанным
в окружность,
если
все его
вершины
многоугольника лежат
на
окружности.
5)
3)
6)
3.
Отравноудалён
центр вписаннойотокружности?
Гдечего
находятся
точки равноудалённые
концов отрезка?
В
О
А
С
4.
Замечание:Теорема
Около
можно описать
только
однуокружность.
окружность.
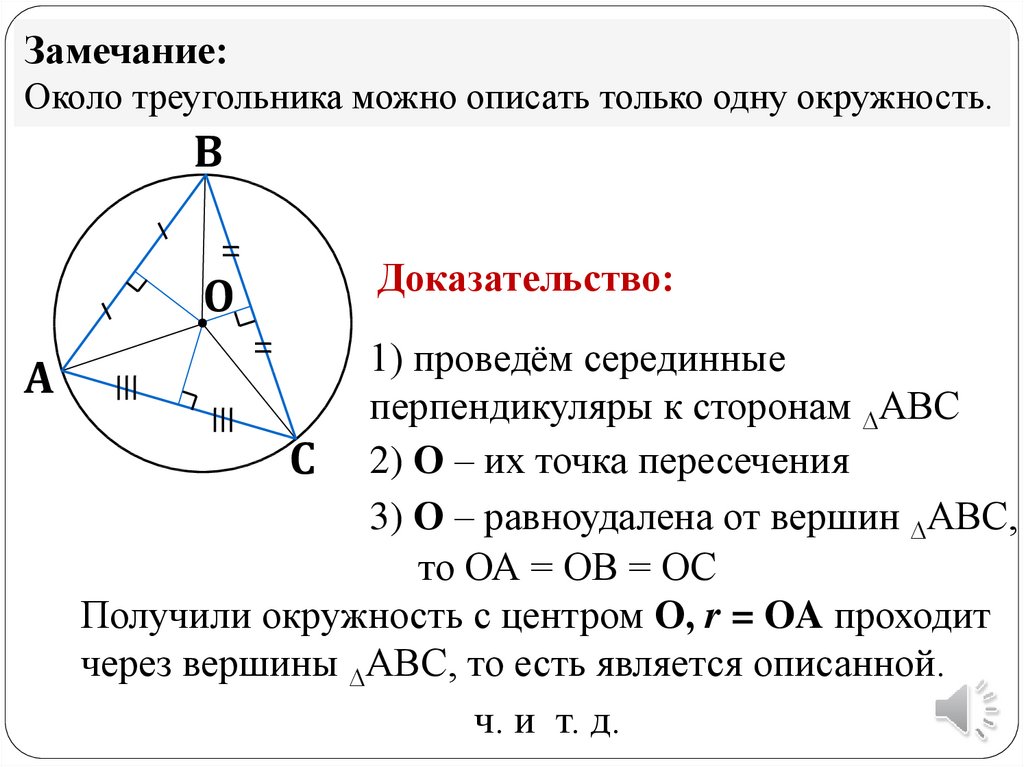
Около треугольника
любого треугольника
можно
описать
В
О
Доказательство:
1) проведём серединные
А
перпендикуляры к сторонам АВС
С 2) О – их точка пересечения
3) О – равноудалена от вершин АВС,
то ОА = ОВ = ОС
Получили окружность с центром О, r = OA проходит
через вершины АВС, то есть является описанной.
ч. и т. д.
5.
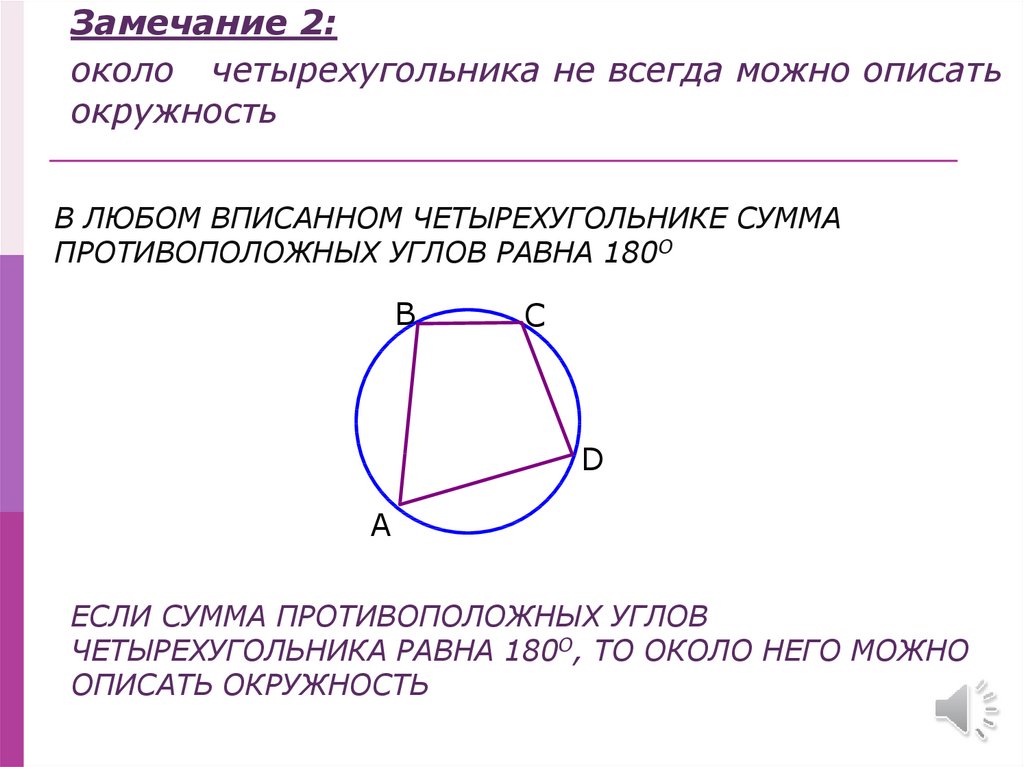
Замечание 2:около четырехугольника не всегда можно описать
окружность
В ЛЮБОМ ВПИСАННОМ ЧЕТЫРЕХУГОЛЬНИКЕ СУММА
ПРОТИВОПОЛОЖНЫХ УГЛОВ РАВНА 180О
B
C
D
A
ЕСЛИ СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ
ЧЕТЫРЕХУГОЛЬНИКА РАВНА 180О, ТО ОКОЛО НЕГО МОЖНО
ОПИСАТЬ ОКРУЖНОСТЬ
6.
№ 702 а)А
С
О
134
В
Дано: окружность,
вписанный АВС так,
что АВ - диаметр окружности
ВС = 134
Найдите углы АВС
7.
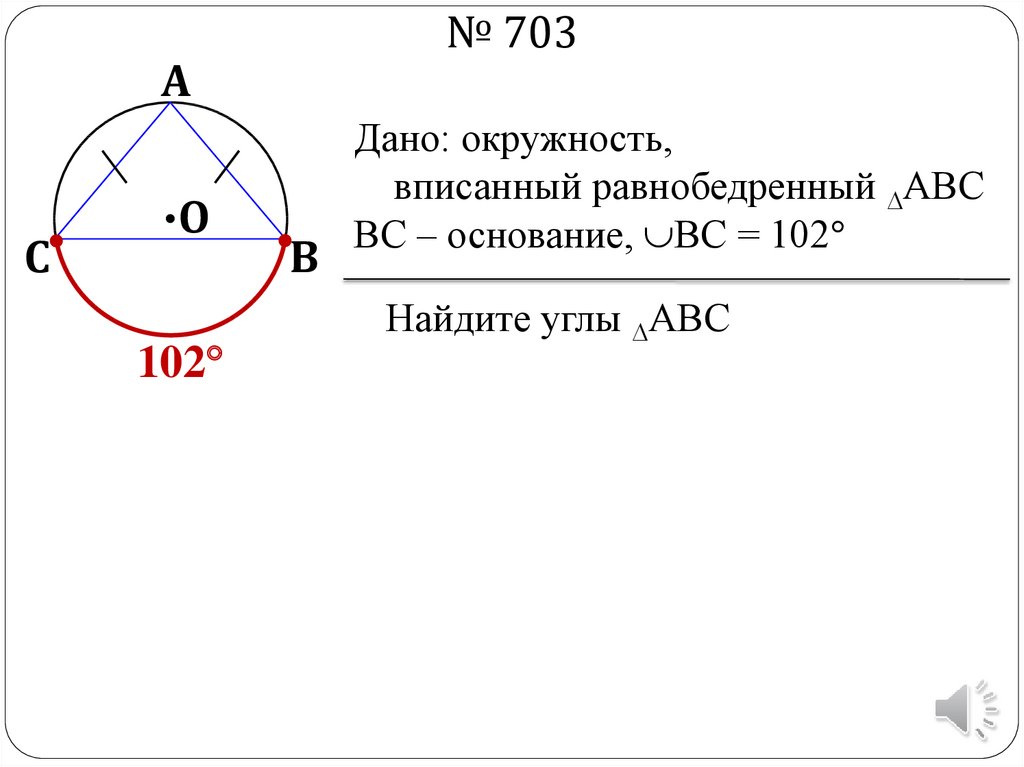
№ 703А
С
О
102
В
Дано: окружность,
вписанный равнобедренный АВС
ВС – основание, ВС = 102
Найдите углы АВС
8.
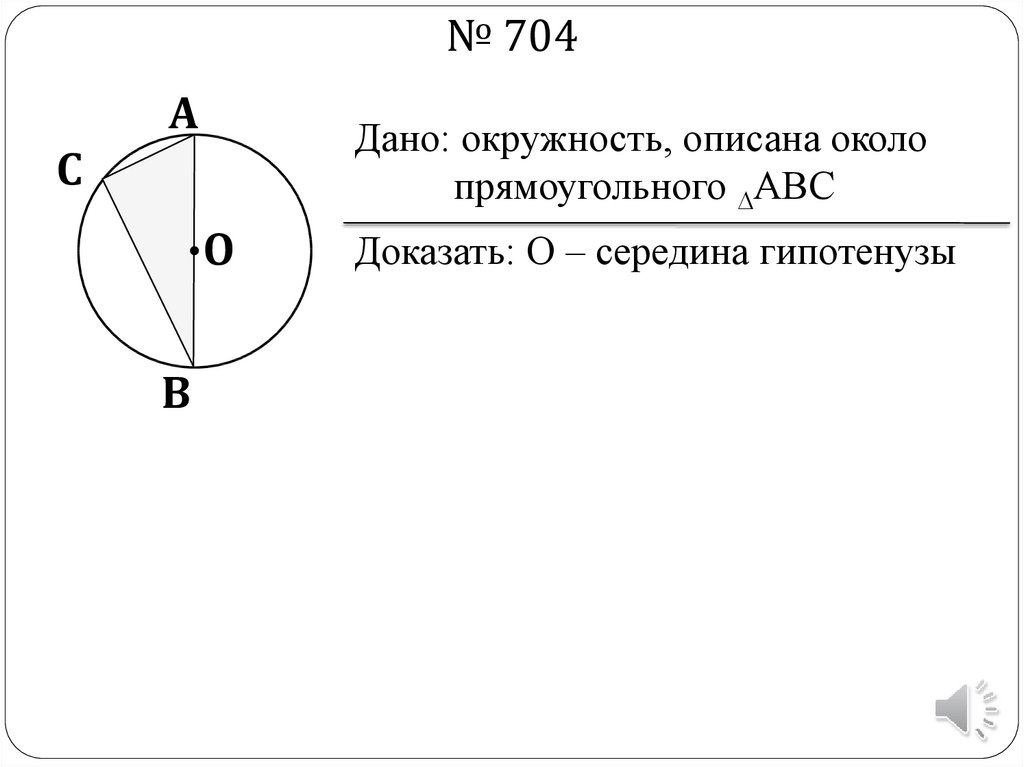
№ 704А
Дано: окружность, описана около
прямоугольного АВС
С
О
В
Доказать: О – середина гипотенузы
9.
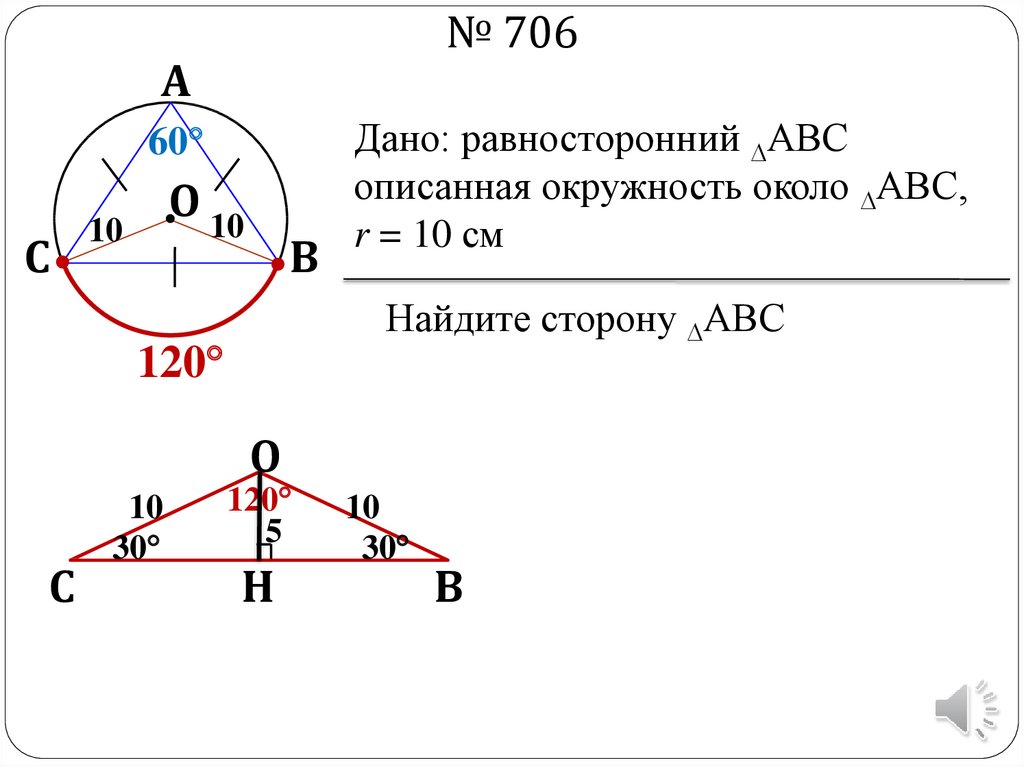
№ 706А
60
С
О 10
10
В
Дано: равносторонний АВС
описанная окружность около АВС,
r = 10 см
Найдите сторону АВС
120
О
С
10
30
120
5
Н
10
30
В
10.
Домашнее заданиеп. 78 выуч. теорию
№ 702 б),
№ 705 а)




 mathematics
mathematics








