Исследования скважин и пластов

1. Исследования скважин и пластов

УЧЕБНЫЙ
КУРС
Исследования скважин и пластов
Москва 2016
Х А Б И Б У Л Л И Н Р. А .

2. Уравнение пьезопроводности

2

3. Сжимаемость

3

4. Предположения уравнения при выводе уравнения фильтрации

•Радиальный режим притока по всей эффективной толщине пласта
•Однородный изотропный пласт постоянной толщины
•Дебит и проницаемость пласта не зависят от давления
•Сжимаемость мала и постоянна
•Вязкость системы постоянна
•Градиент давления мал
•Гравитационные силы пренебрежимо малы
4

5. Безразмерные переменные

Безразмерные переменные позволяют выделить переменные влияющие на
поведение системы и избавиться от лишних неизвестных, производных от других
величин
Уравнение записанное в безразмерных переменных не зависит от выбора системы
размерностей
Решение уравнения фильтрации
5

6. Безразмерные переменные

Безразмерные переменные для практических метрических систем единиц
Безразмерное давление
PD =
kh
DP
18.41qB m
Безразмерное время
tD =
0.00036kt
jm ct rw2
t DA =
0.00036kt
jm ct A
tD =
0.00036kt
jm ct x 2f
Связанное с радиусом скважины
Связанное с областью дренирования скважины
Связанное с размерами трещины
Безразмерный коэффициент ствола скважины
CD =
0.159
Cs
hj ct rw2
6

7. Решение уравнения фильтрации

•Для того чтобы найти решение уравнения фильтрации
необходимо задать начальное и граничные условия
•Задание начального и граничного условий – задает модель
интерпретации ГДИС
•Наиболее распространенные модели
◦
◦
◦
◦
◦
◦
◦
Модель постоянного дебита
Модель постоянного давления
Модель линейного стока (маленький радиус скважины)
Модель замкнутого пласта
Модель пласта с поддержание давления на границе
Модель скважины с трещиной гидроразрыва
и т.д.
7

8. Решение линейного стока

Начальное условие
Условие постоянного дебита в
скважине малого радиуса
Условие бесконечного пласта
Решение линейного стока уравнения
фильтрации
8

9.

g = 0.57721566
- Ei ( - x ) = E1 ( x ) = - ln( x ) - g
Постоянная Эйлера
9

10. Постоянная Эйлера—Маскерони

Постоянная Эйлера—Маскерони
Материал из Википедии — свободной энциклопедии
или постоянная Эйлера — математическая константа, определяемая как
предел разности между частичной суммой гармонического ряда и
натуральным логарифмом числа:
Постоянная ЭЭ́йлера—МаскероЭ́ни
Константа введена Леонардом Эйлером в 1735, который предложил для неё
обозначение C, которое до сих пор иногда применяется. Итальянский математик
Лоренцо Маскерони в 1790 вычислил 32 знака константы и предложил современное
обозначение γ.
Значение константы:
γ ≈ 0,577215664901532860606512090082402431042159335
9399235988057672348848677267776646709369470632917467495…
Постоянная Эйлера может быть выражена как интеграл:
Через неё выражается производная Гамма-функции, например, γ = − Γ'(1).
В теории чисел нередко используется константа
eγ ≈ 1,78107241799019798523650410310717954916964521430343…
10

11. Решение линейного стока

pD ( rD , t D )
1 æ rD2 ö
= - Ei ç ÷
2 è 4t D ø
Логарифмическая аппроксимация решения
pD ( rD , t D )
pD ( rD , t D )
æ rD2
1æ
= çç - ln ç
2è
è 4t D
ö
ö
÷ - g ÷÷
ø
ø
ö 1 æ æ tD ö
ö
1 æ æ tD ö
= çç ln ç 2 ÷ + ( ln ( 4 ) - g ) ÷÷ = çç ln ç 2 ÷ + 0.809 ÷÷
2 è è rD ø
ø 2 è è rD ø
ø
Логарифмическая аппроксимация имеет место при
rD2
< 0.01
4t D
11

12. Применимость решения линейного стока

Решение линейного стока в размерных переменных
12

13. Применимость решения линейного стока

Решение линейного стока в практических метрических
переменных
18.41qs B m æ 1 æ
fm ct r 2 ö ö
p ( r , t ) = pi ç - Ei ç ÷÷
kh
2
0.00144
kt
è
øø
è
p ( r , t ) = pi -
ö
9.205qs B m æ
kt
ln
7.12
ç
÷
2
kh
fm
c
r
t
è
ø
kt
> 70000
fm ct r 2
p ( r , t ) = pi -
ö
9.205qs Bm æ 1
kt
log e
log
7.12
ç
÷
2
kh
log
e
fm
c
r
log
e
t
è
ø
p ( r , t ) = pi -
ö
21.195qs Bm æ
kt
3.09
ç log
÷
2
kh
fm
c
r
t
è
ø
13

14. Упражнение

•Построить в Excel решение линейного стока и его
логарифмическую аппроксимацию
•Представить полученные решения в полулогарифмических
координатах
•Определить диапазон применимости логарифмической
аппроксимации решения линейного стока с размерных и
безразмерных переменных
14

15. Применимость решения линейного стока

Для бесконечного однородного пласта поведения давления при тесте на
падение давления описывается решением для линейного стока
ö
9.205qs B m æ
-fm ct r 2
p ( r , t ) = pi Ei
+
2
S
ç
÷
kh
kt
è
ø
p ( r , t ) = pi -
ö
9.205qs B m æ
kt
7.12
+
2
S
ç ln
÷
2
kh
fm
c
r
t
è
ø
Для практических метрических единиц
15

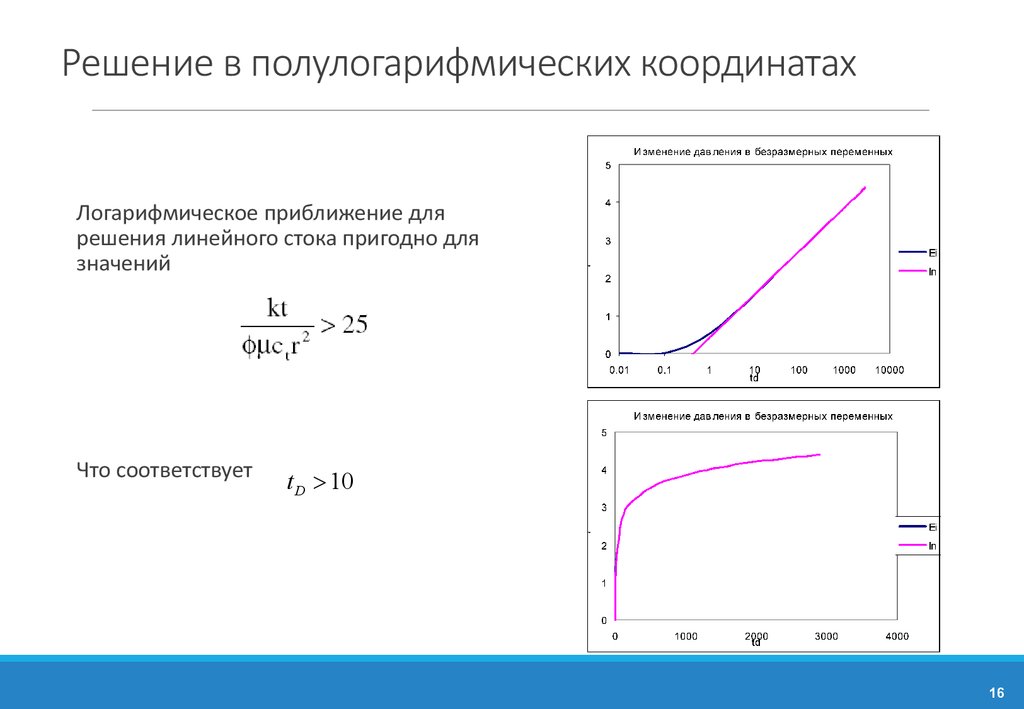
16. Решение в полулогарифмических координатах

Логарифмическое приближение для
решения линейного стока пригодно для
значений
Что соответствует
t D > 10
16

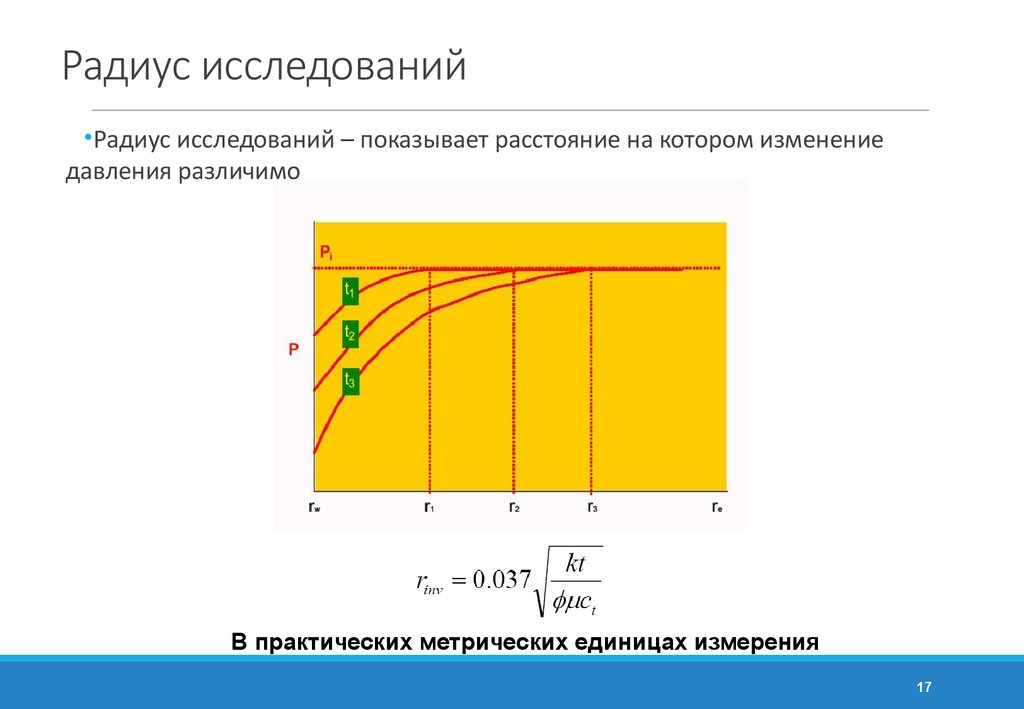
17. Радиус исследований

•Радиус исследований – показывает расстояние на котором изменение
давления различимо
В практических метрических единицах измерения
17

18. Упражнение. Радиус исследований

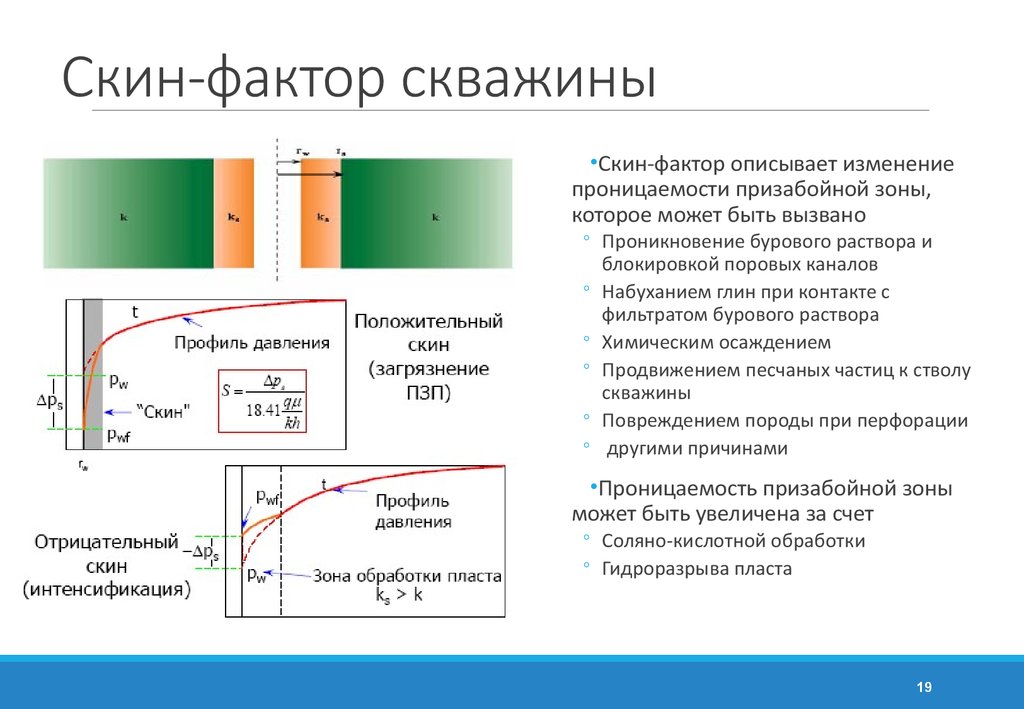
18

19. Скин-фактор скважины

•Скин-фактор описывает изменение
проницаемости призабойной зоны,
которое может быть вызвано
◦ Проникновение бурового раствора и
блокировкой поровых каналов
◦ Набуханием глин при контакте с
фильтратом бурового раствора
◦ Химическим осаждением
◦ Продвижением песчаных частиц к стволу
скважины
◦ Повреждением породы при перфорации
◦ другими причинами
•Проницаемость призабойной зоны
может быть увеличена за счет
◦ Соляно-кислотной обработки
◦ Гидроразрыва пласта
19

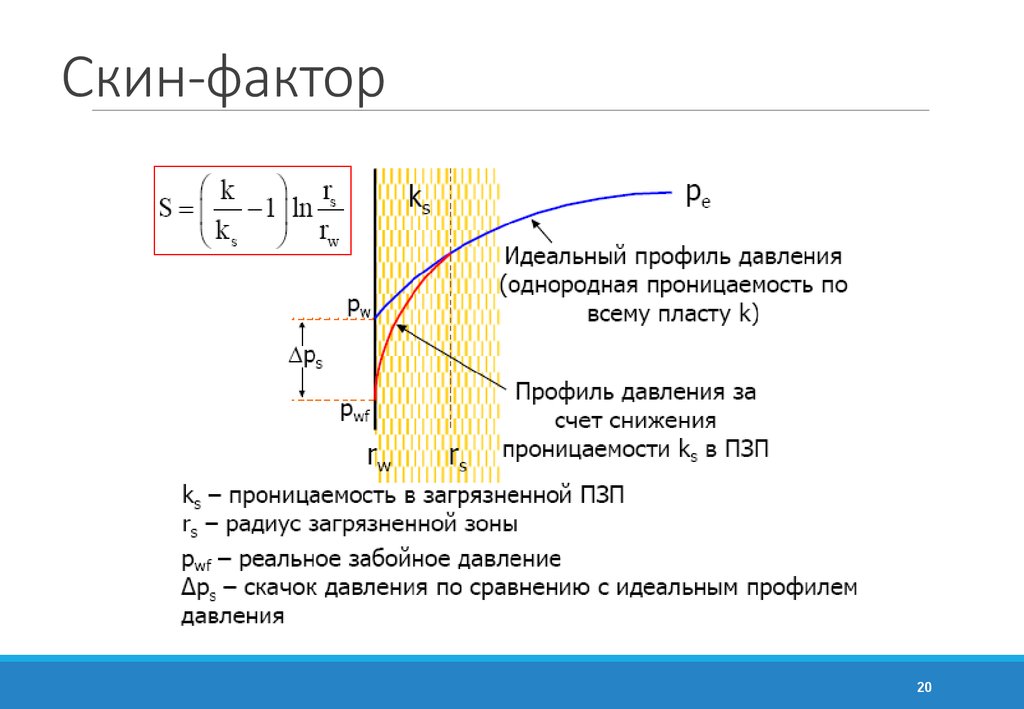
20. Скин-фактор

20

21. Скин-фактор

Скин-фактор в уравнении установившегося притока в радиальном пласте
Продуктивность скважины определяется как
p ( r , t ) = pi -
ö
9.205qs B m æ
kt
ln
+
7.12
+
2
S
ç
÷
2
kh
fm
c
r
t
è
ø
21

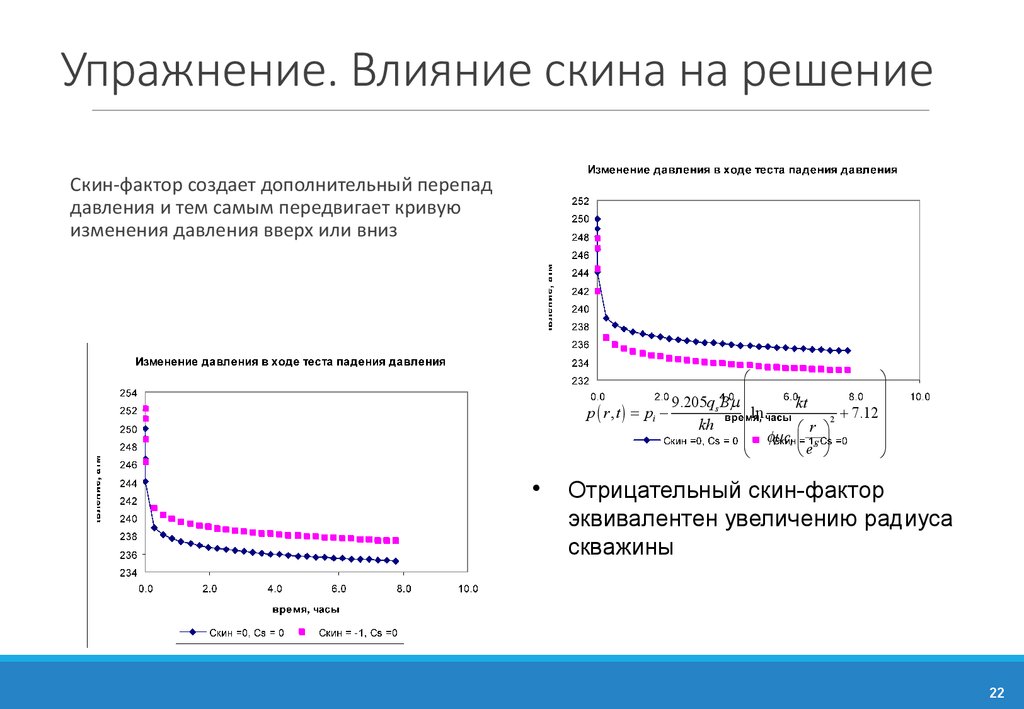
22. Упражнение. Влияние скина на решение

Скин-фактор создает дополнительный перепад
давления и тем самым передвигает кривую
изменения давления вверх или вниз
æ
ö
ç
÷
9.205qs B m ç
kt
p ( r , t ) = pi ln
+ 7.12 ÷
2
ç
÷
kh
æ r ö
ç fm ct ç S ÷
÷
èe ø
è
ø
Отрицательный скин-фактор
эквивалентен увеличению радиуса
скважины
22

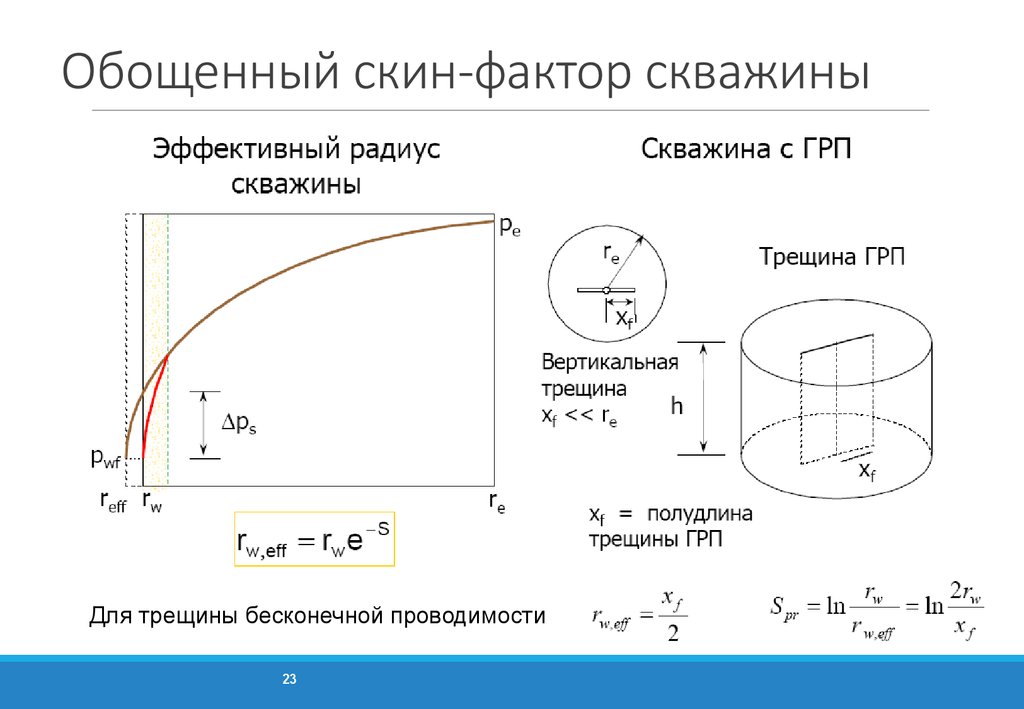
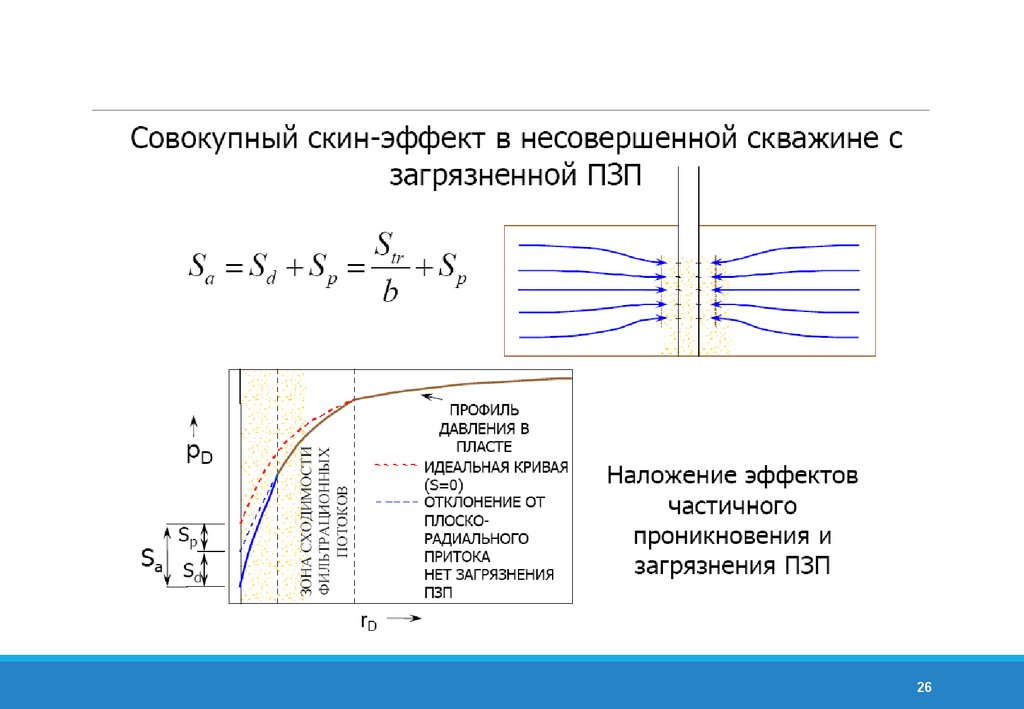
23. Обощенный скин-фактор скважины

Для трещины бесконечной проводимости
23

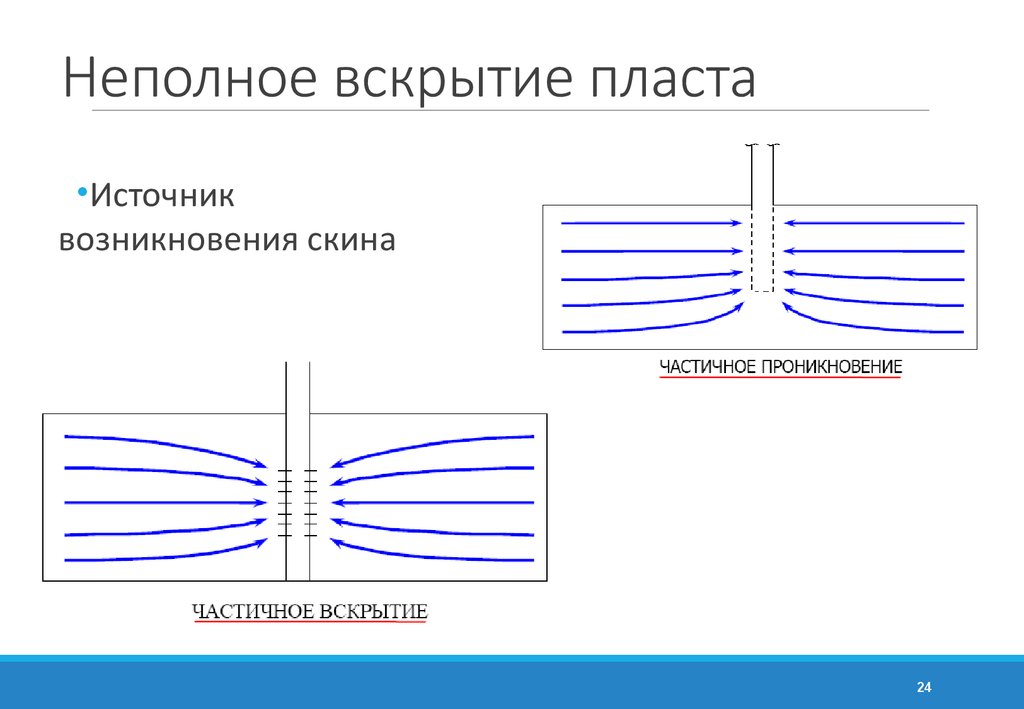
24. Неполное вскрытие пласта

•Источник
возникновения скина
24

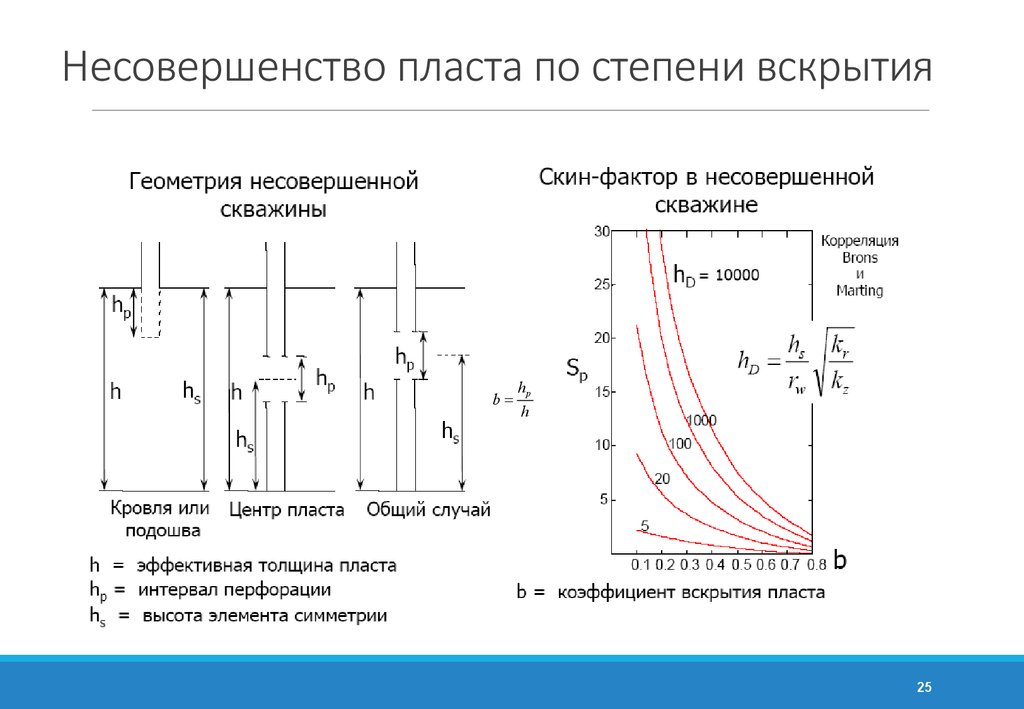
25. Несовершенство пласта по степени вскрытия

b=
hp
h
25

26.

26

27.

Обобщенный скин-фактор
Stotal включает:
SMеханический (загрязнение, стимуляция)
SФлюиды (влияние газа, многофазного потока)
SЗаканчивания (трещины гидроразрыва, частичное вскрытие, наклонные скважины)
SГеологический (анизотропия, естественная трещиноватость)
Диапазоны изменения скин-фактора (по Грингартену)
SМеханический
SГаз
=
-4 (после кислотной обработки) → +20 (загрязнение)
=
+5 → +20
SМногофазный=
+5 → +15
SAнизотропии =
-2 → 0
SЗаканчивания =
-5.5 (трещины, горизонтальные скважины) → +300 (неполное вскрытие)
Sгеологический
=
-3 (геоскин в трещиноватых коллекторах) → 0
27

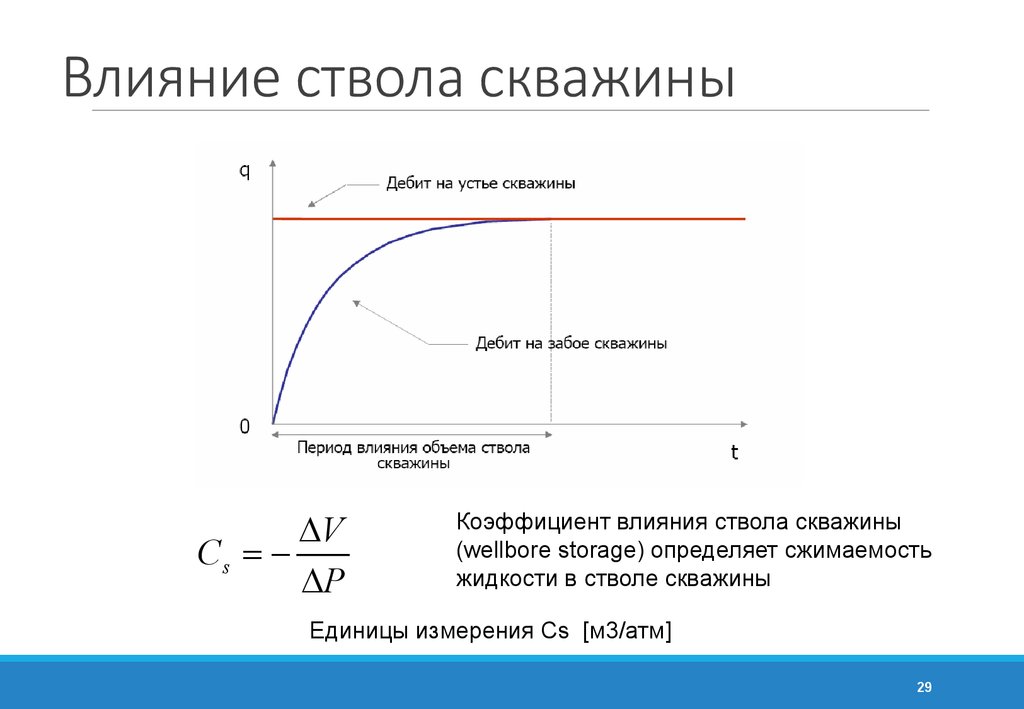
28. Влияние ствола скважины (послеприток)

28

29. Влияние ствола скважины

DV
Cs = DP
Коэффициент влияния ствола скважины
(wellbore storage) определяет сжимаемость
жидкости в стволе скважины
Единицы измерения Cs [м3/атм]
29

30. Влияние ствола скважины

Для фонтанирующей скважины
Изменение объема жидкости в стволе скважины происходит за счет
сжимаемости жидкости
DV = -cVw DP
DV
Cs = DP
Единицы измерения Cs [м3/атм]
Для фонтанирующей скважины, коэффициент ствола скважины
Cs = cVw
Vw
c
Объем жидкости в стволе скважины [м3]
Сжимаемость жидкости в стволе скважины [1/атм]
30

31. Влияние ствола в фонтанирующей скважине

Глубина скважины
Диаметр НКТ
2000 м
70 мм
Сжимаемость жидкости в стволе скважины
1*10-5 1/атм
Cs = cVw
d2
0.0702
Vw = p
L = 3.14 ×
× 2000 = 7.7
4
4
Cs = cVw = 7.7 ×10
-5
м3
[м3/атм]
31

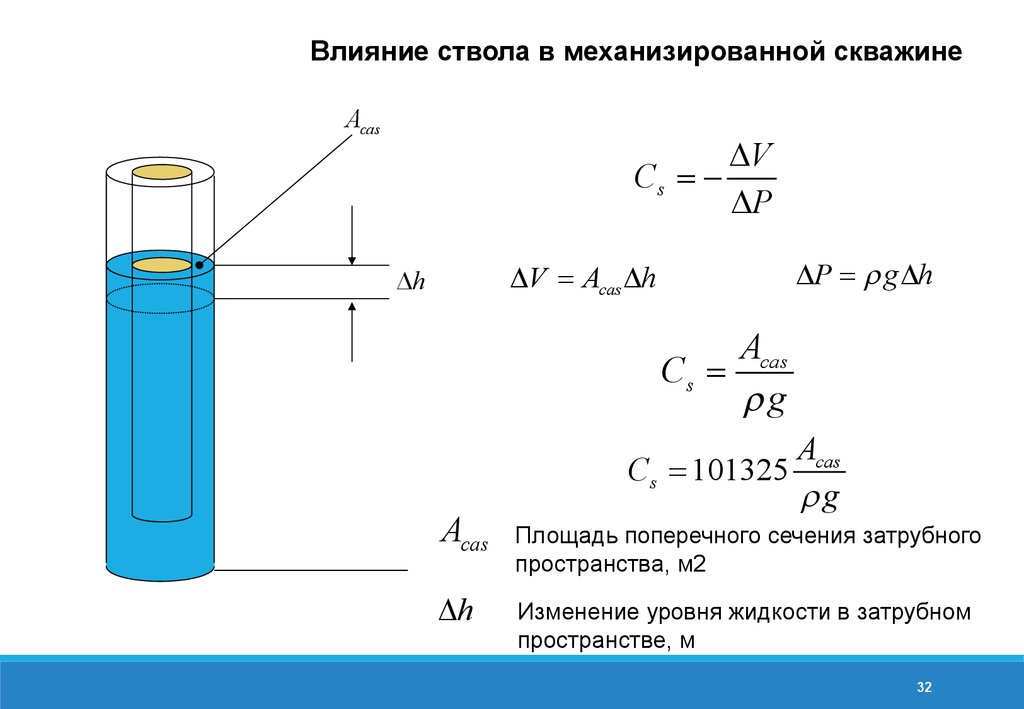
32.

Влияние ствола в механизированной скважине
Acas
DV
Cs = DP
DP = r g Dh
DV = Acas Dh
Dh
Acas
Cs =
rg
Acas
Dh
Acas
Cs = 101325
rg
Площадь поперечного сечения затрубного
пространства, м2
Изменение уровня жидкости в затрубном
пространстве, м
32

33. Влияние ствола в механизированной скважине

Глубина скважины
2000 м
Диаметр НКТ
73 мм
Диаметр эксп. коллоны
137 мм
Плотность нефти 866 кг/м3
Acas
Cs = 101325
rg
Acas
p 2
3.14
2
= ( d cas - dtub ) =
0.137 2 - 0.0732 ) = 0.01
(
4
4
Acas
0.01
Cs = 101325
= 101325
= 0.12
rg
9.8 × 866
м2
[м3/атм]
Чему равна величина коэффициента ствола скважины, если в затрубном
пространстве находится газо-нефтая смесь плотностью 500 кг/м3?
33

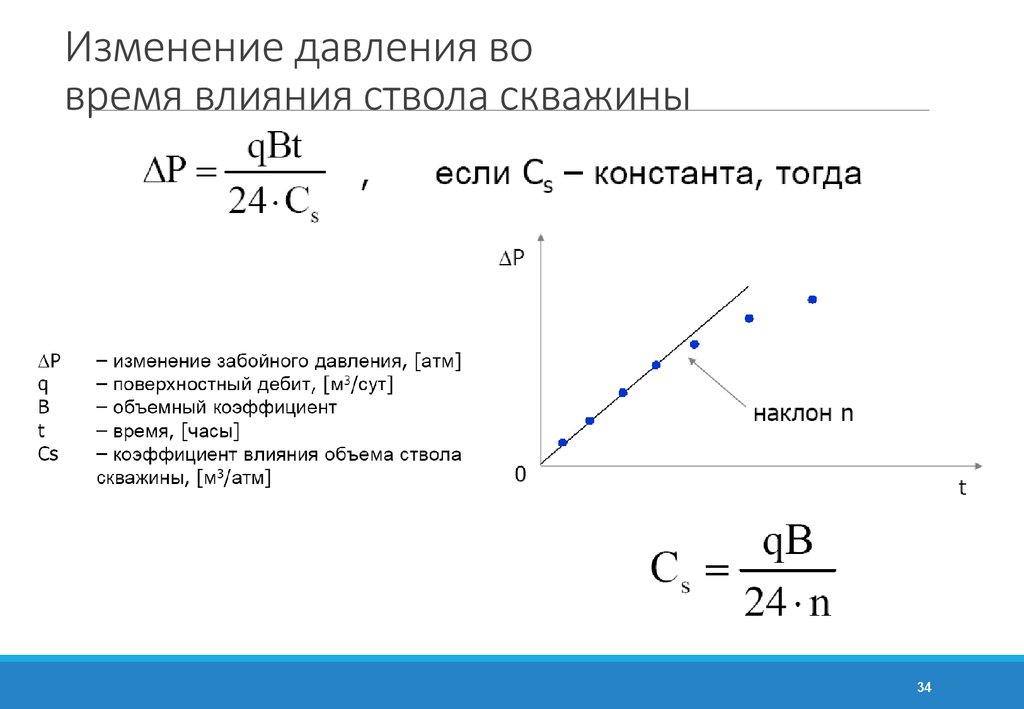
34. Изменение давления во время влияния ствола скважины

34

35.

35

36. Приток из пласта

24Cs dP
qf = q +
B dt
36

37. Определение периода влияния ствола скважины

Существует три правила определения конца периода влияния ствола скважины
- Правило Рамея (Ramey)
twbs =
( 26531 + 1547 S ) Cs
kh
m
- Правило Чена и Бригхама (Chen and Brigham)
twbs
22109Cs e0.14 S
=
kh
m
где
k
- проницаемость, [миллидарси];
h
m
– мощность пласта, [м];
S
– скин-фактор;
– вязкость, [сП];
37

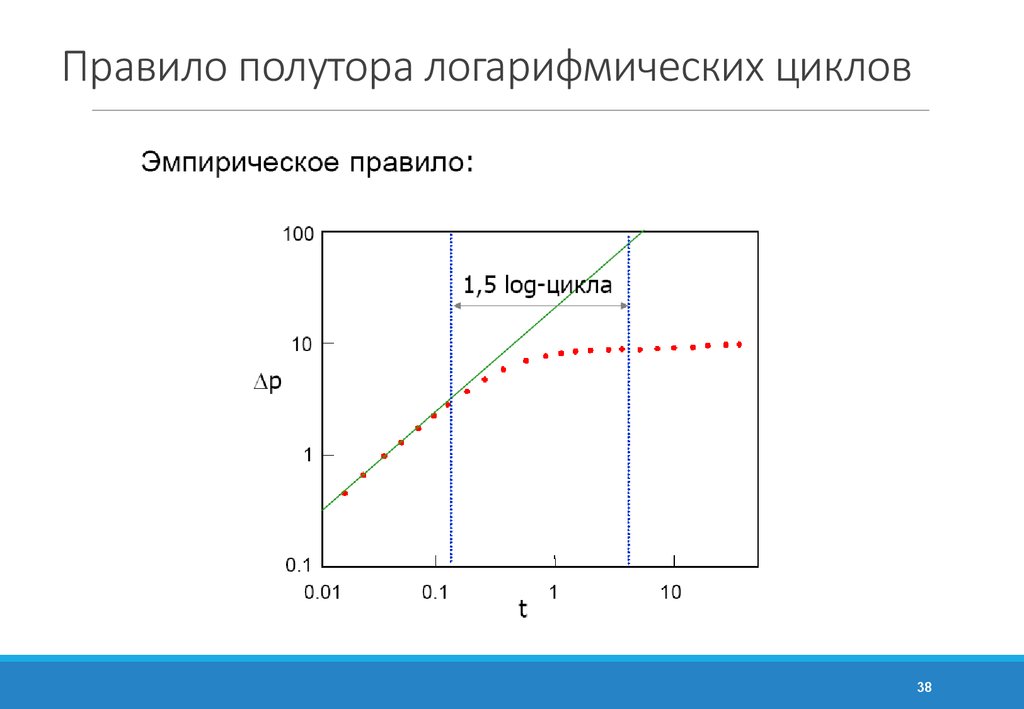
38. Правило полутора логарифмических циклов

38

39. Решение уравнения фильтрации

•Решение уравнения фильтрации для бесконечного пласта,
конечного радиуса скважины с учетом
скин – фактора и послепритока
Решение в пространстве Лапласа имеет вид
Решение в действительных переменных находится с
использованием алгоритма Стефеста
39

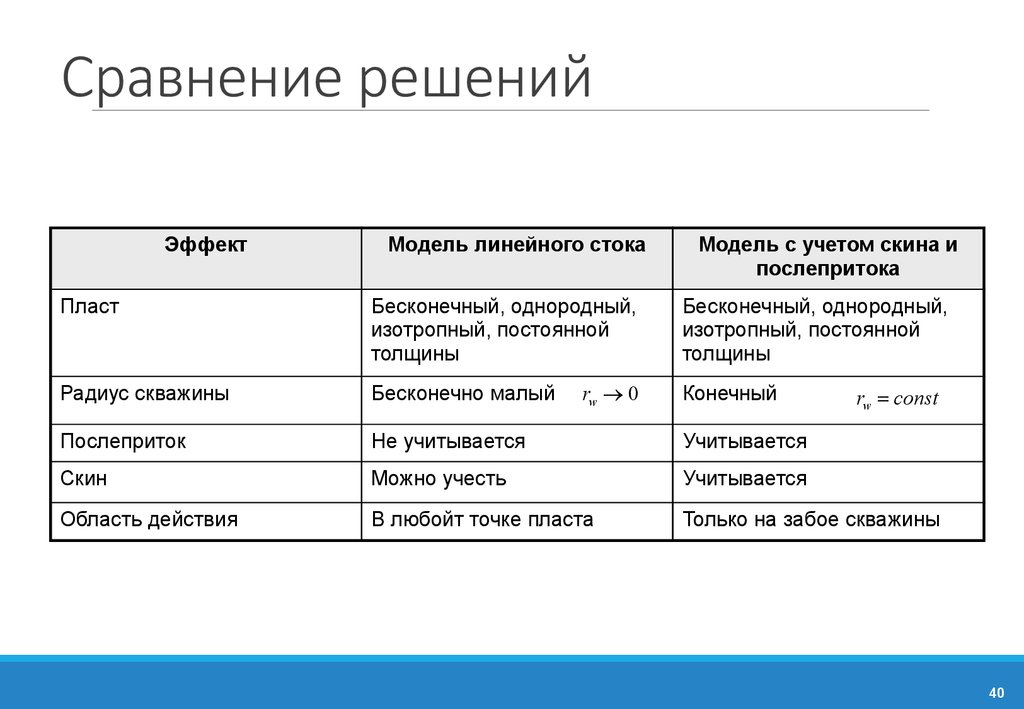
40. Сравнение решений

Эффект
Модель линейного стока
Модель с учетом скина и
послепритока
Пласт
Бесконечный, однородный,
изотропный, постоянной
толщины
Радиус скважины
Бесконечно малый
Послеприток
Не учитывается
Учитывается
Скин
Можно учесть
Учитывается
Область действия
В любойт точке пласта
Только на забое скважины
rw ® 0
Бесконечный, однородный,
изотропный, постоянной
толщины
Конечный
rw = const
40

41. Упражнение

•Построить решение уравнения фильтрации для бесконечного
пласта с учетом скин – фактора и послепритока скважины в Excel с
использованием функции Stehfest
◦ Исследовать влияния скин-фактора на решение
◦ Исследовать влияние послепритока в скважину на решение
◦ Сравнить решение с решением линейного стока и его логарифмическим
приближением
41

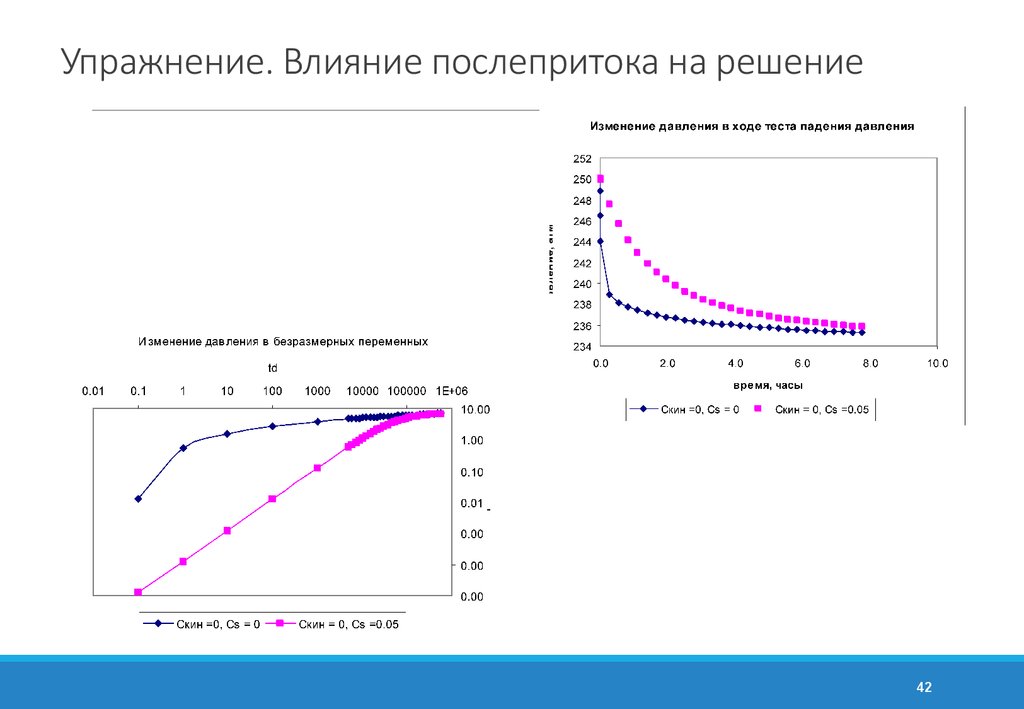
42. Упражнение. Влияние послепритока на решение

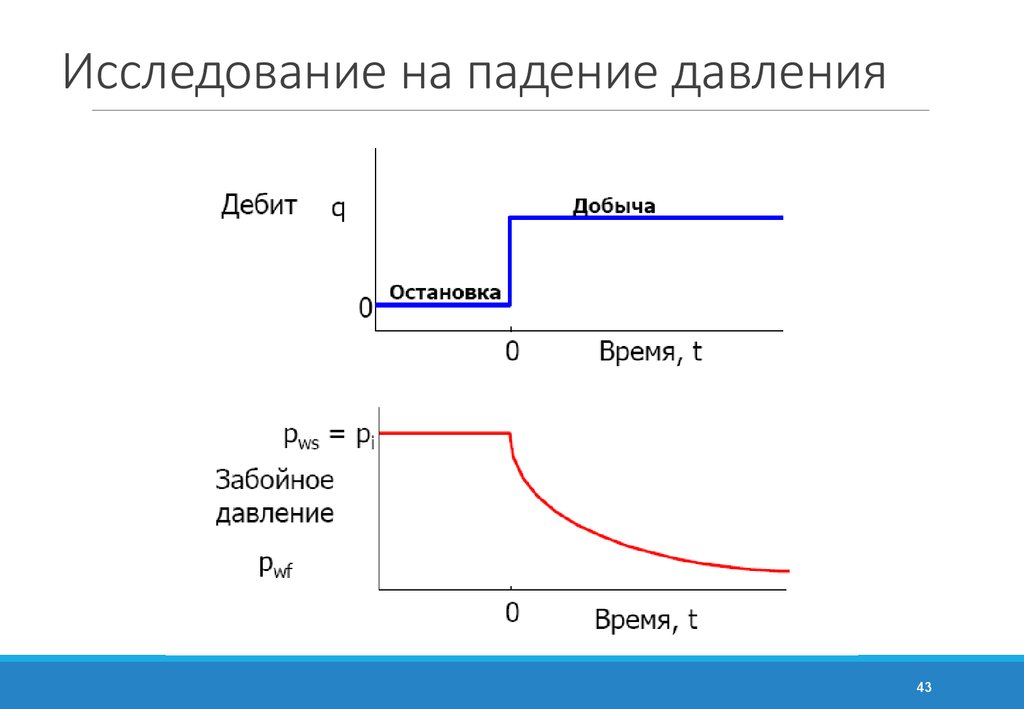
42

43. Исследование на падение давления

43

44. Применимость решения линейного стока

Для бесконечного однородного пласта поведения давления при тесте на
падение давления описывается решением для линейного стока
ö
9.205qs B m æ
-fm ct r 2
p ( r , t ) = pi Ei
+
2
S
ç
÷
kh
kt
è
ø
p ( r , t ) = pi -
ö
9.205qs B m æ
kt
7.12
+
2
S
ç ln
÷
2
kh
fm
c
r
t
è
ø
Для практических метрических единиц
44

45. Решение в полулогарифмических координатах

Логарифмическое приближение для
решения линейного стока пригодно для
значений
Что соответствует
t D > 10
45

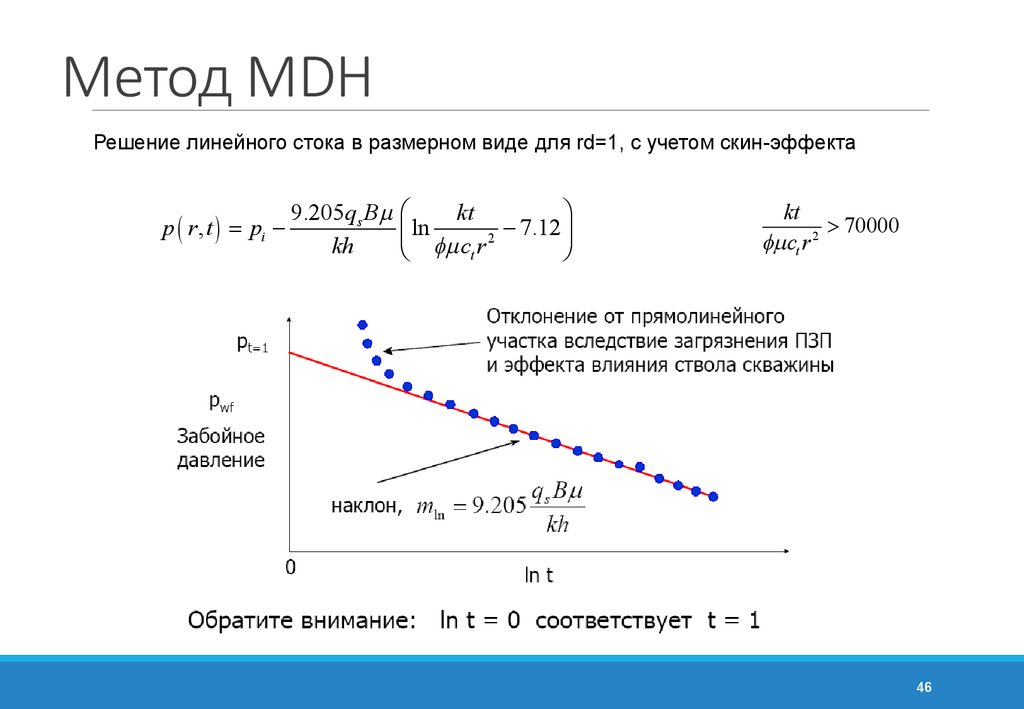
46. Метод MDH

Решение линейного стока в размерном виде для rd=1, с учетом скин-эффекта
p ( r , t ) = pi -
ö
9.205qs Bm æ
kt
ln
7.12
ç
÷
2
kh
fm
c
r
t
è
ø
kt
> 70000
fm ct r 2
46

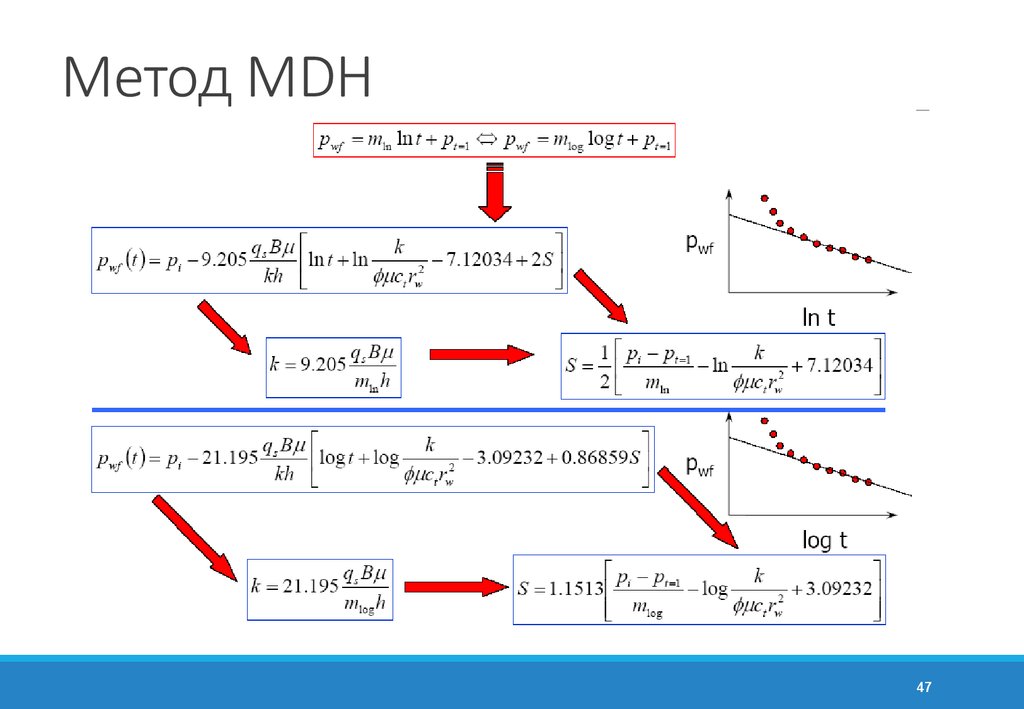
47. Метод MDH

47

48. Метод MDH

Для радиального притока к скважине, можно записать
pwf = mln ln t + pt =1
pwf ( t ) = pi - 9.205
ù
qs B m é
k
ln
t
+
ln
7.12034
+
2
S
ê
ú
kh ë
fm ct rw2
û
Откуда, можно выразить
q Bm
k = 9.205 s
mln h
ù
1 é pi - pt =1
k
pwf ( t ) S = ê
- ln
+ 7.12034 ú
2
2 ë mln
fm ct rw
û
48

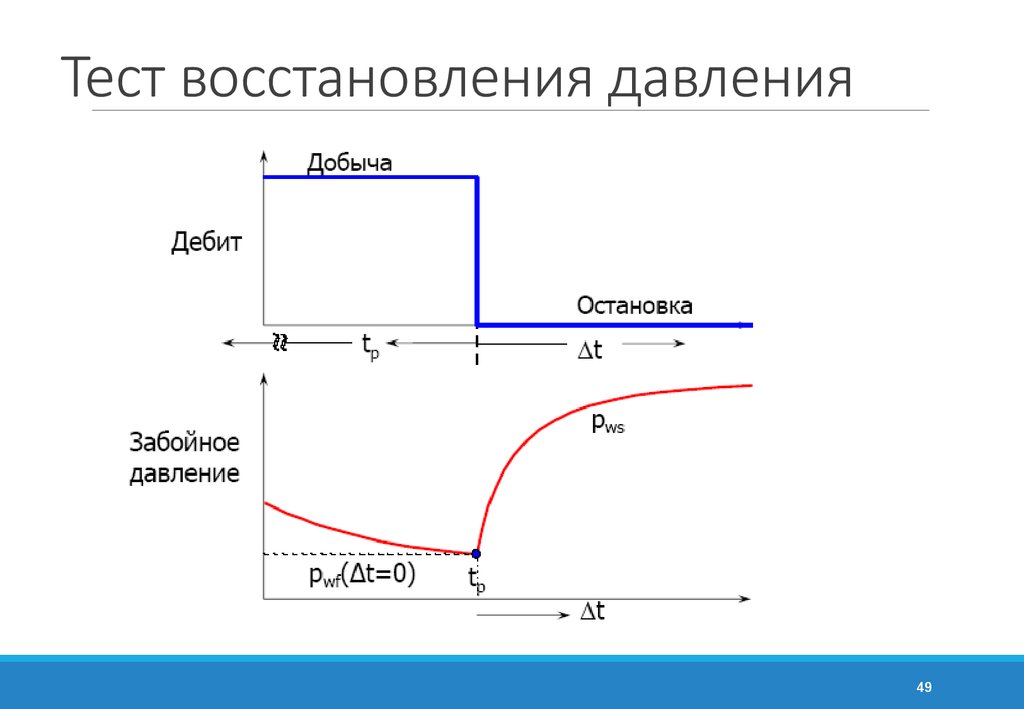
49. Тест восстановления давления

49

50. Тест восстановления давления

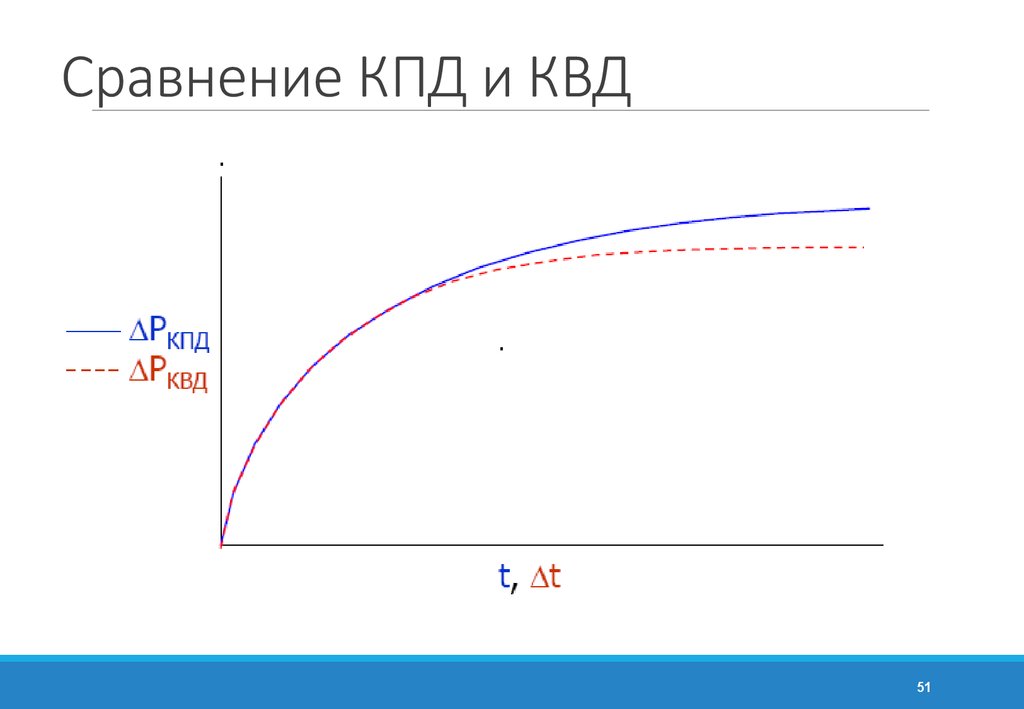
50

51. Сравнение КПД и КВД

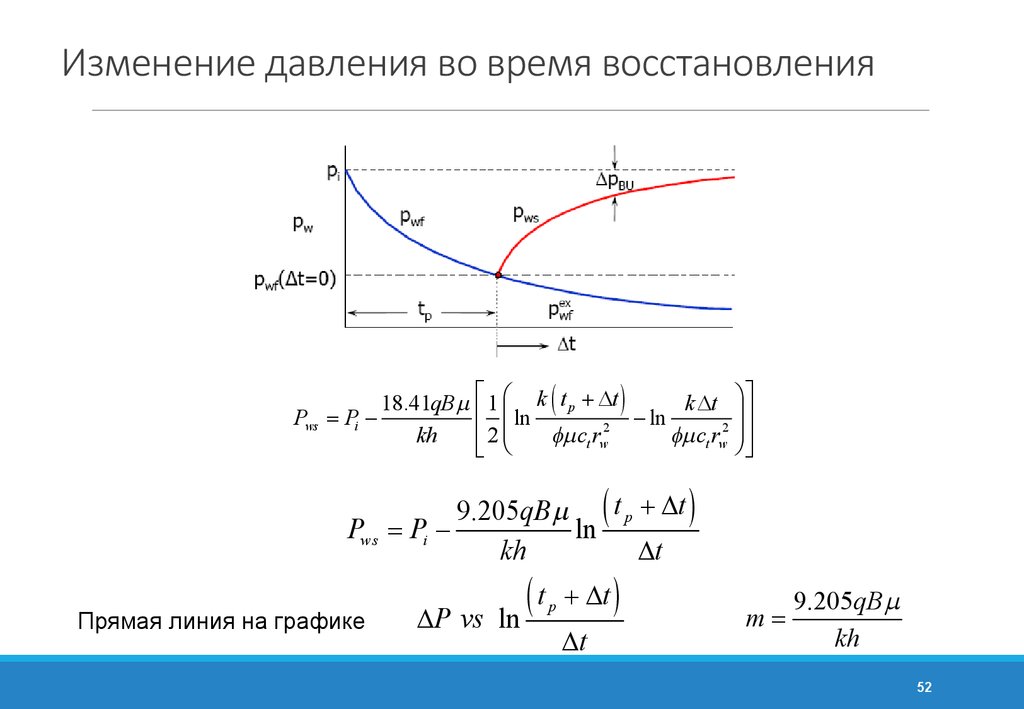
51

52. Изменение давления во время восстановления

18.41qB m
Pws = Pi kh
é 1 æ k ( t p + Dt )
k Dt ö ù
ê ç ln
÷ú
- ln
2
2
ç
fm ct rw
fm ct rw ÷ø ú
êë 2 è
û
9.205qB m ( t p + Dt )
Pws = Pi ln
kh
Dt
Прямая линия на графике
DP vs
t
(
ln
p
+ Dt )
Dt
m=
9.205qB m
kh
52

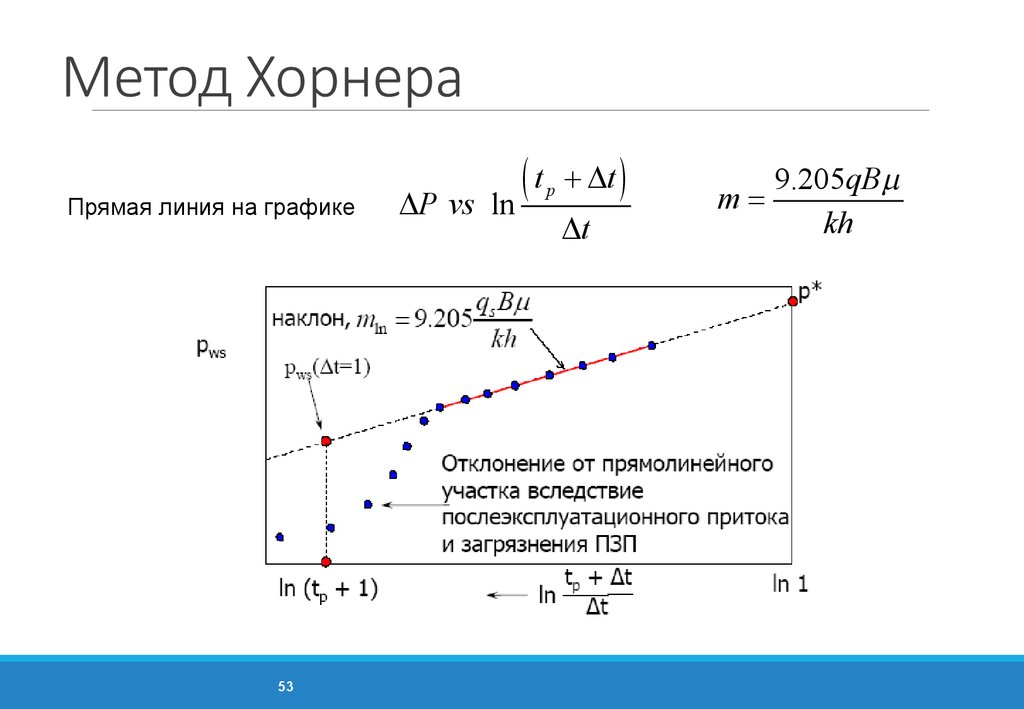
53. Метод Хорнера

Прямая линия на графике
53
DP vs
t
(
ln
p
+ Dt )
Dt
9.205qB m
m=
kh

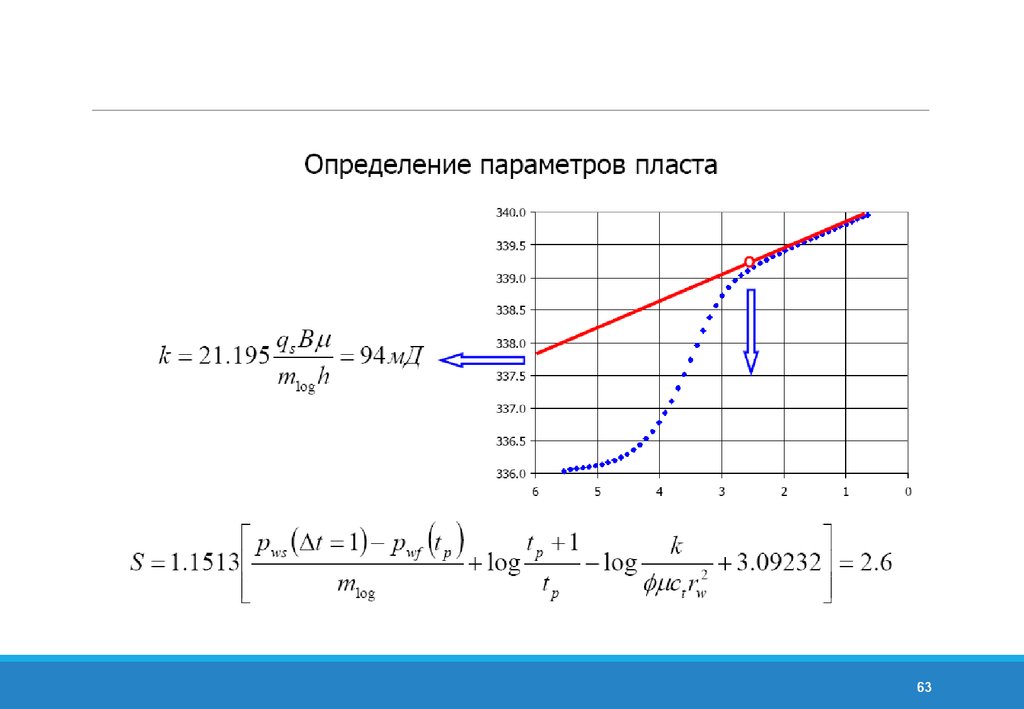
54. Вычисление скин-фактора по методу Хорнера

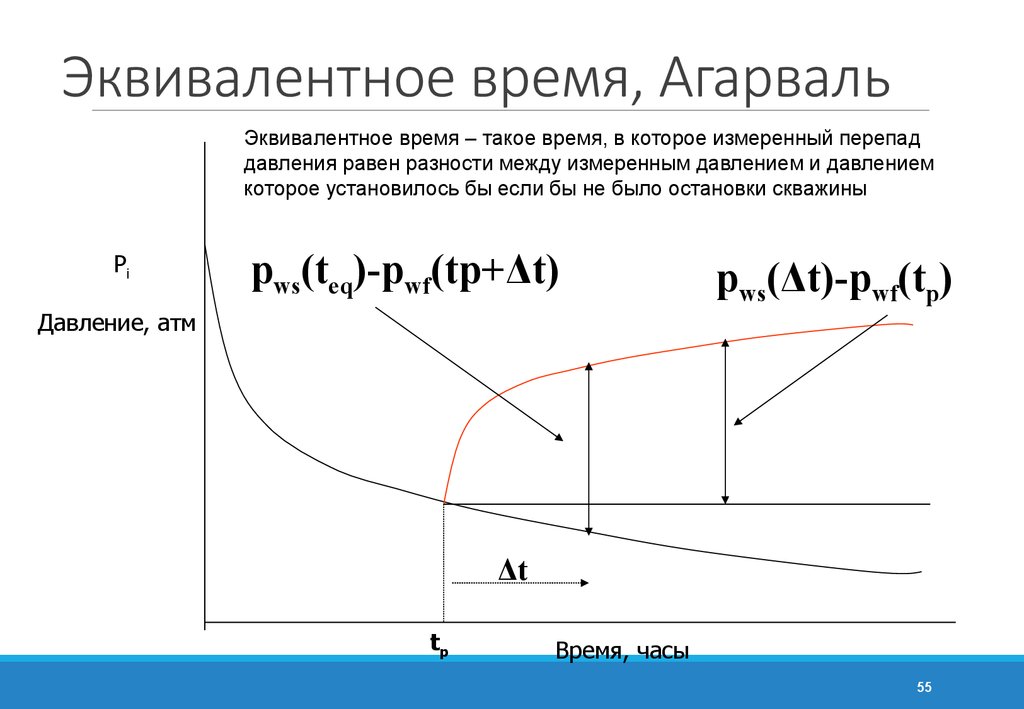
54

55. Эквивалентное время, Агарваль

Эквивалентное время – такое время, в которое измеренный перепад
давления равен разности между измеренным давлением и давлением
которое установилось бы если бы не было остановки скважины
Pi
pws(teq)-pwf(tp+Δt)
pws(Δt)-pwf(tp)
Давление, атм
Δt
tp
Время, часы
55

56. Эквивалентное время

te =
t p Dt
t p + Dt
N
q j - q j -1
j =1
qN
log te =
é t j - t j -1 + Dt ù
log ê
ú
Dt
ë
û
56

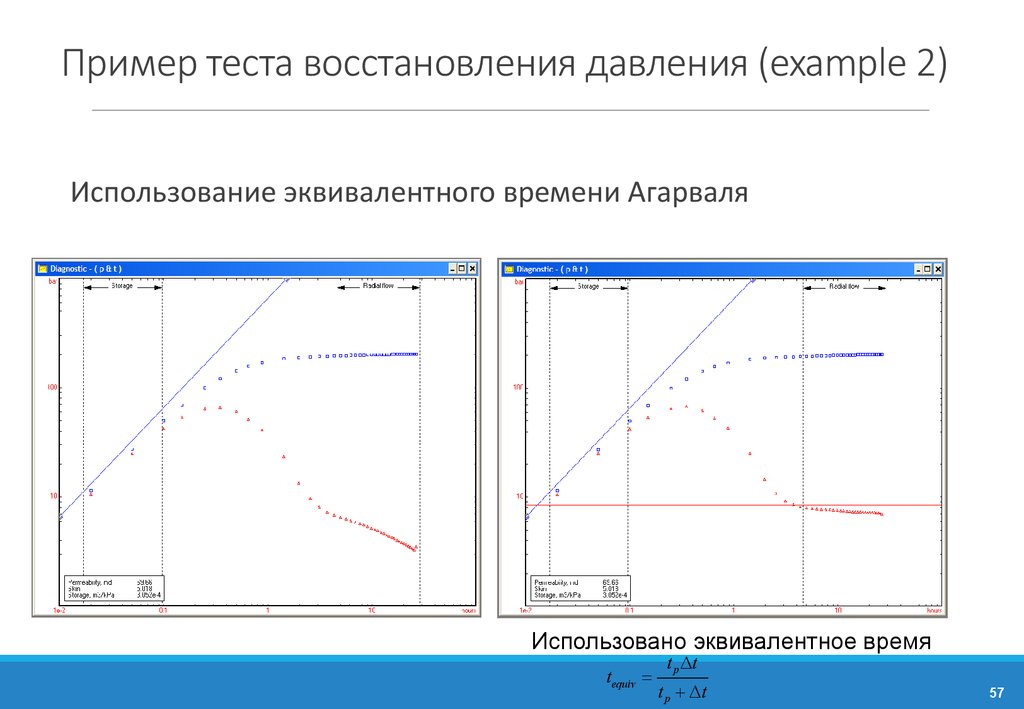
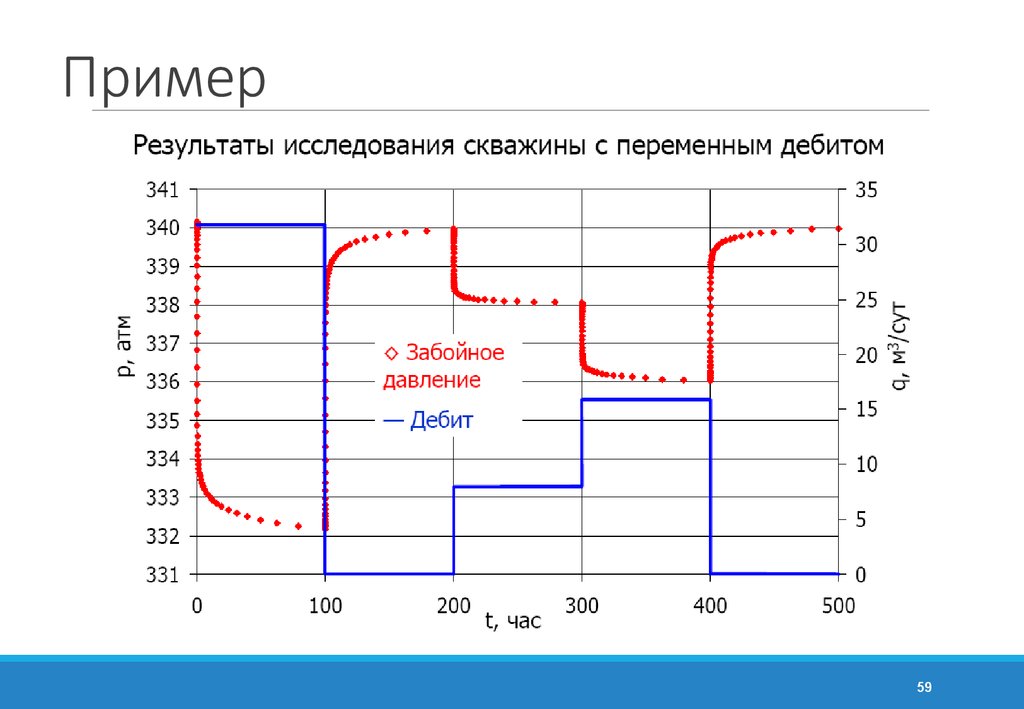
57. Пример теста восстановления давления (example 2)

Использование эквивалентного времени Агарваля
Использовано эквивалентное время
tequiv =
t p Dt
t p + Dt
57

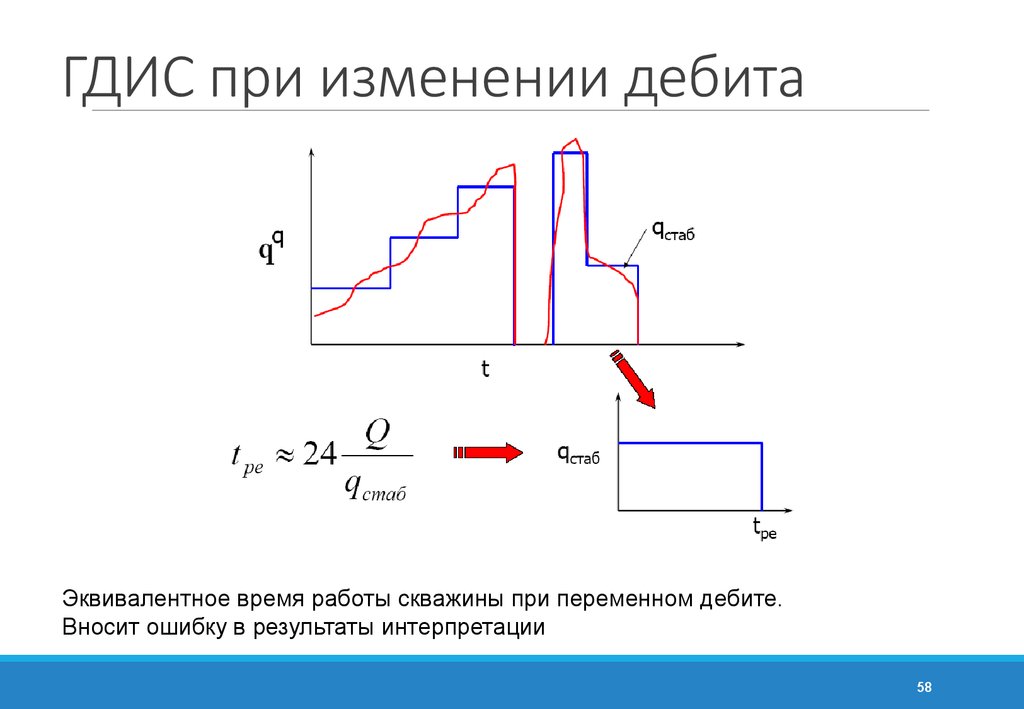
58. ГДИС при изменении дебита

Эквивалентное время работы скважины при переменном дебите.
Вносит ошибку в результаты интерпретации
58

59. Пример

59

60.

60

61.

61

62.

62

63.

63