Similar presentations:
Решение двойных неравенств, решение неравенств с одной переменной. 8 класс
1.
Урок алгебры в 8 классе.1
2.
Решение неравенствс одной переменной.
2
3.
Теоретическая разминкаНеравенством называется - запись, в которой два числа или
два выражения, содержащие переменные,
соединены знаком >, < , ≥ или ≤.
Линейными неравенствами с одной переменной называют
неравенства вида ах > b или ах < b,
где а и b – некоторые числа.
Решением неравенства с одной переменной называется
значение переменной, которое обращает его в
верное числовое неравенство.
Решить неравенство –
значит найти все его решения
или доказать, что их нет.
3
4.
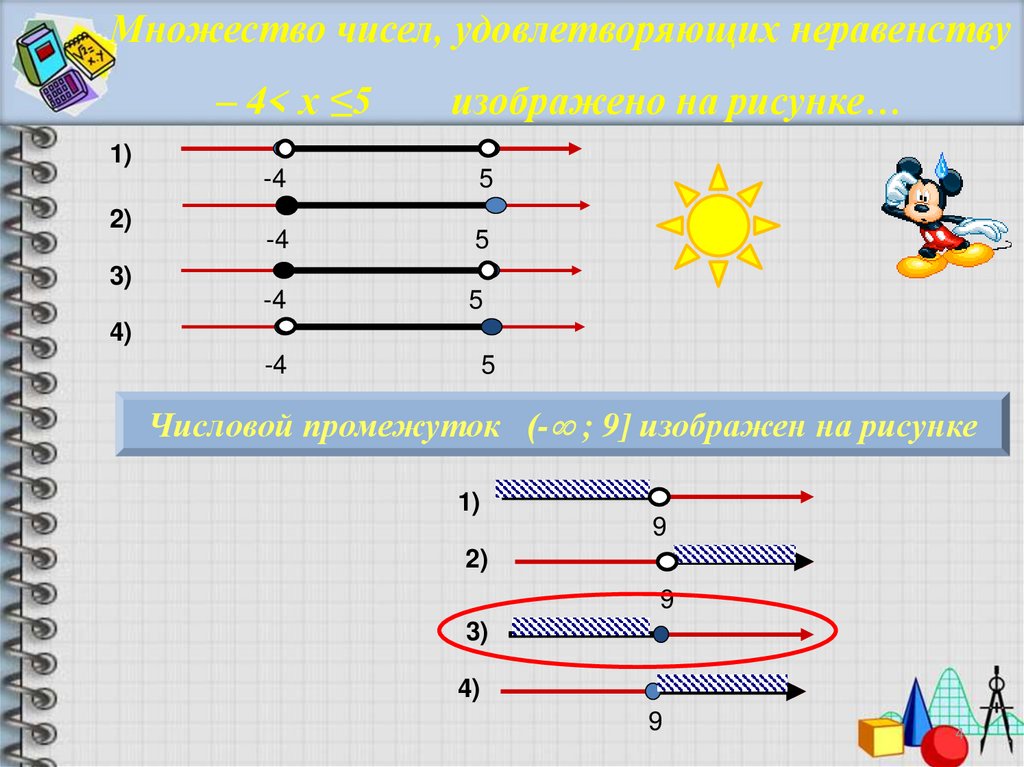
Множество чисел, удовлетворяющих неравенству– 4< х ≤5
изображено на рисунке…
1)
2)
-4
5
-4
5
-4
5
4
3)
4)
-4
5
Числовой промежуток (- ; 9] изображен на рисунке
1)
9
2)
9
3)
4)
9
4
5.
Установите соответствие между неравенствоми числовым промежутком
1. Х ≥ 12
а. (12;+ )
2. 3 < Х ≤ 18
б. (3; 18)
3. Х ˃ 12
в. [12; + )
4. -4 ≤ Х < 0
г. (3; 18]
5. 3 < Х < 18
д. [4; 12]
6. -4 ≤ Х ≤ 0
е. [-4; 0)
5
6.
На координатной прямой отмечены числа а и b.Какое из приведенных утверждений неверно?
1) а b < 0
3) а + b < 0
2)
4) а2 b ˃ 0
а - b ˃0
6
7.
Решите неравенство6x 2 3x 7
Перенесем в левую часть
слагаемые с переменной, а
в правую - без переменной
6x 3x 7 2
Приведём подобные слагаемые
3x 9
Разделим обе части неравенства
на положительное число 3,
сохраняя при этом знак
x 3
неравенства:
-3
Ответ:
; 3
Изобразим
множество решений
на координатной прямой
7
8.
Решите неравенствоСамостоятельно с самопроверкой
2x 1 3x 2 x 6x 3
6 x x 2 6 x 3x
2
2
6 x x 6 х 3х 2
2
4x < 2
x 0,5
2
|2:-4
При делении
на отрицательное число
не забудь поменять знак неравенства
на противоположный.
-0,5
Ответ: 0,5;
8
9.
Внимание ошибки!3х - 3 < 5х+4
3х – 5х < 3 + 4
- 2х < 7
х<
˃ -3,5
-3,5
Ответ:
3,;
5;
3,5
9
10.
Решите неравенство(взаимопроверка)
( 6 х + 1 )2 – 21 < ( 4 х + 2 )(9 х – 1 )
36x2 + 12x + 1 – 21 < 36x2 + 18x – 4x – 2
12x – 14x < 20 – 2
– 2x < 18
x > - 9.
Ответ:
( - 9; + ∞ ).
10
11.
Решите неравенствох х
>2
3 2
х
х
6 6 > 2 ∙ 6
3
2
Умножим обе части неравенства на
наименьший общий знаменатель дробей,
входящих в неравенство,
т. е. на положительное число 6
2х – 3х > 12
- х > 12
х < - 12
- 12
Ответ: (- ∞; -12)
11
12.
При каких значениях переменнойимеет смысл выражение:
7
5 х 10
28 7 а
5х – 10 ≥ 0
28 - 7а ˃ 0
5х ≥ 10
х≥2
2
-7а ˃ -28
а<4
4
Ответ: 2;
Ответ:
;4
12
13.
Решите двойное неравенство- 12 < 5 – x < 17
-5 - 12 < -х < 17 - 5
-17 < -х < 12
: (-1)
-12 < х < 17
-12
17
Ответ:(-12 ; 17)
13
14.
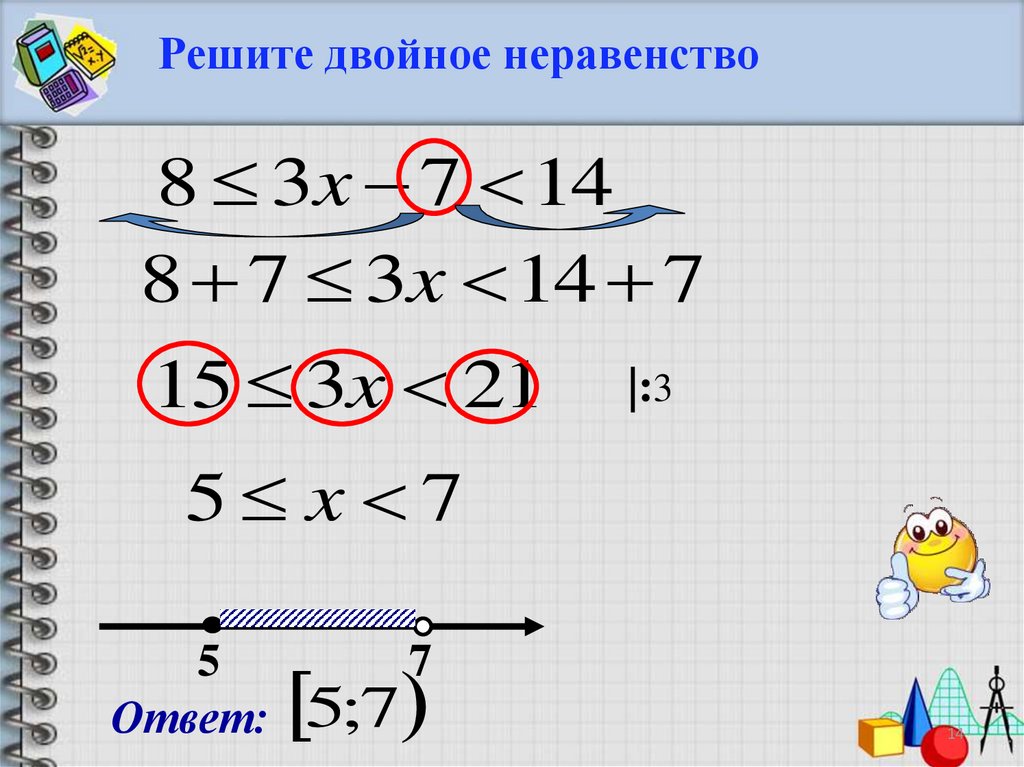
Решите двойное неравенство8 3x 7 14
8 7 3x 14 7
15 3x 21
|:3
5 x 7
5
Ответ:
7
5;7
14
15.
Решение неравенств ах > b илипри а = 0.
ах < b
Линейное неравенство вида 0∙х < b или 0∙х > b,
а значит и соответствующее ему исходное неравенство,
либо не имеет решений,
либо его решением является любое число.
Пример 1. 0∙х < 48
Ответ: х – любое число
Пример 2. 0∙х < - 7
Ответ: нет решений.
15
16.
Распределите неравенства в два столбика,в зависимости от ответа:
1)
0∙х < 7
5)
2)
0∙x < -7
0∙х ≤ 0
НЕ имеет решений
3)
6)
0∙х ≥ 6
4)
0∙х > -5
0∙x > 0
х - любое число
16
17.
Тестирование.(Ответ да - 1, нет- 0 )1) Является ли число 12 решением неравенства 2х > 10?
2) Верно ли утверждение: если х >2 и y >14, то х + y < 16?
3) Является ли неравенство 5х-15 > 4х+14 строгим?
4) Решением неравенства 5х -1< 4 является (1; +∞) ?
5) При любом ли значении переменной а верно
неравенство а² +4 > 0?
6) Верно ли, что при умножении или делении обеих частей
неравенства на отрицательное число
знак неравенства не меняется?
ПРОВЕРИМ!
101010
17
18.
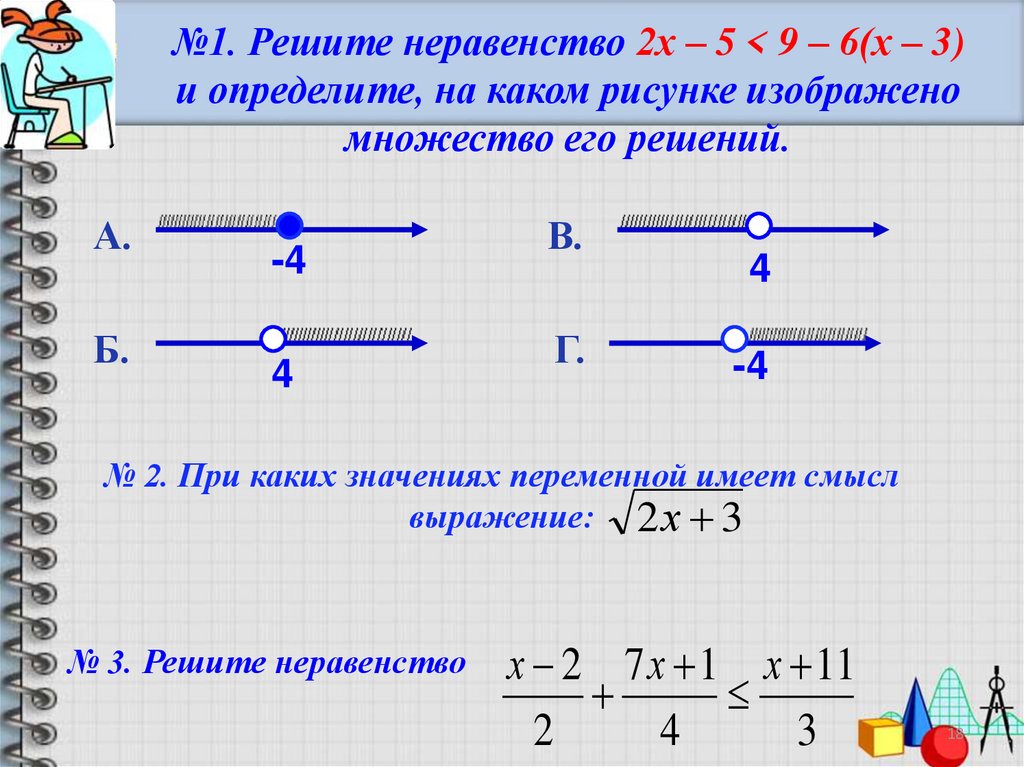
№1. Решите неравенство 2х – 5 < 9 – 6(х – 3)и определите, на каком рисунке изображено
множество его решений.
А.
Б.
-4
4
В.
Г.
4
-4
№ 2. При каких значениях переменной имеет смысл
выражение: 2 х 3
№ 3. Решите неравенство
х 2 7 х 1 х 11
2
4
3
18
19.
Историческая справкаПонятиями неравенства пользовались уже древние греки.
Например, Архимед (III в. до н. э.), занимаясь вычислением
длины окружности, указал границы числа «пи».
10
1
3 3
71
7
Ряд неравенств приводит в своём трактате «Начала» Евклид.
Современные знаки неравенств < > появились лишь
в 17-18 вв. Их ввел английский математик Томас Гарриот.
Символы и ≥ были введены в 1734 году французским
математиком Пьером Буге́ром.
19
















 mathematics
mathematics








