Similar presentations:
Опредление Производной
1.
2. Угловой коэффициент прямой.
Прямая проходит через началокоординат и точку Р(3; -1). Чему
равен ее угловой коэффициент?
1 3k
1
k
3
3. Найдите угловые коэффициенты прямых:
21
1
4
2
3
3
4
4. Секущая и касательная к кривой.
5.
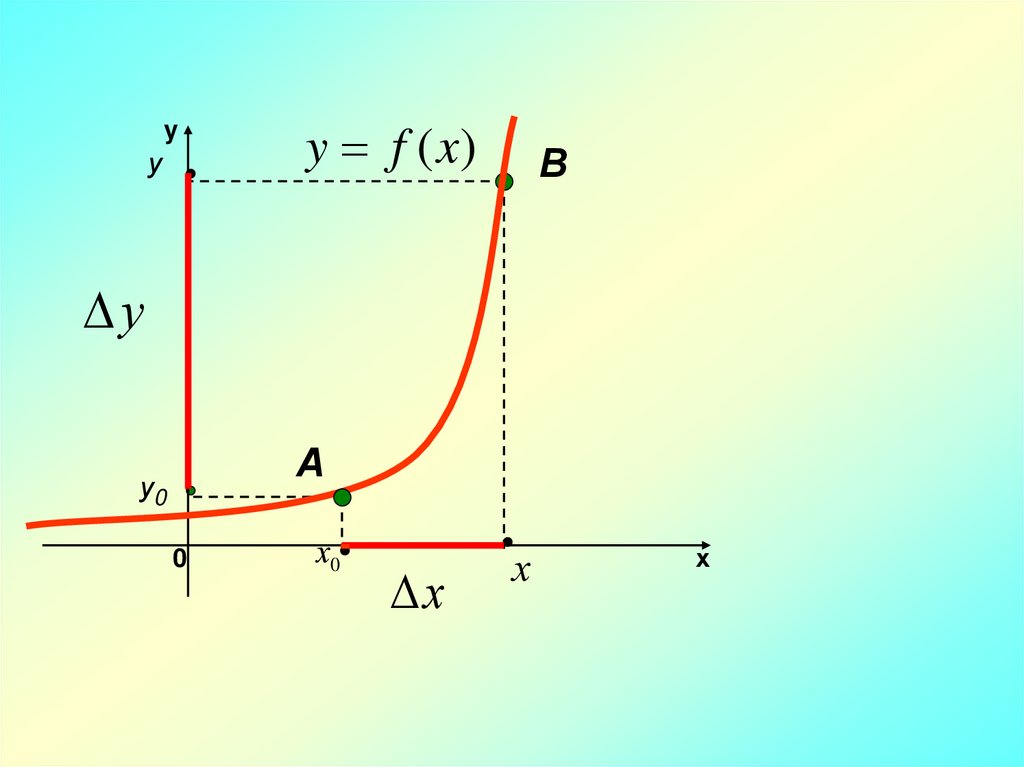
yу
y f (x)
В
у
А
у0
0
х0
х
х
х
6.
При х 0 угловой коэффициен т секущей к угловомукоэффициен ту касательной.
y
у
y f (x)
k – угловой
коэффициент
прямой(секущей)
В
y
k
x
y
y
у0
0
А
х0
х 0
х
х
х
Секущая стремится занять положение касательной.
Касательная есть предельное положение секущей.
7.
yy f (x)
Угловой коэффициент
касательной
можно найти как
предел выражения:
f ( x) f ( x0 )
kкас lim
x x0
x x0
y
0
х0
х
0
х
х
Касательную охарактеризовали как
предельное положение секущей при
приближении к 0
8.
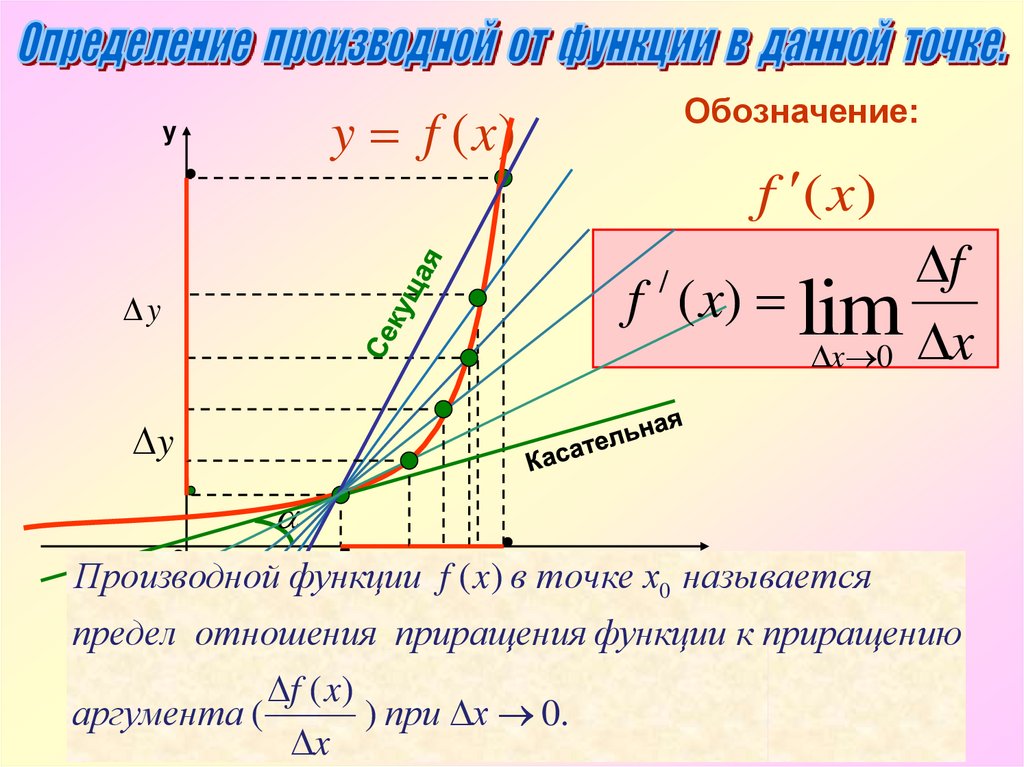
Обозначение:y f (x)
y
f (x)
f
f ( x) lim
x 0 x
/
y
y
х0
х
х
Производной функции
х f (0x) в точке х0 называется
0
предел отношения приращения функции к приращению
f ( x)
аргумента (
) при х 0.
x
9.
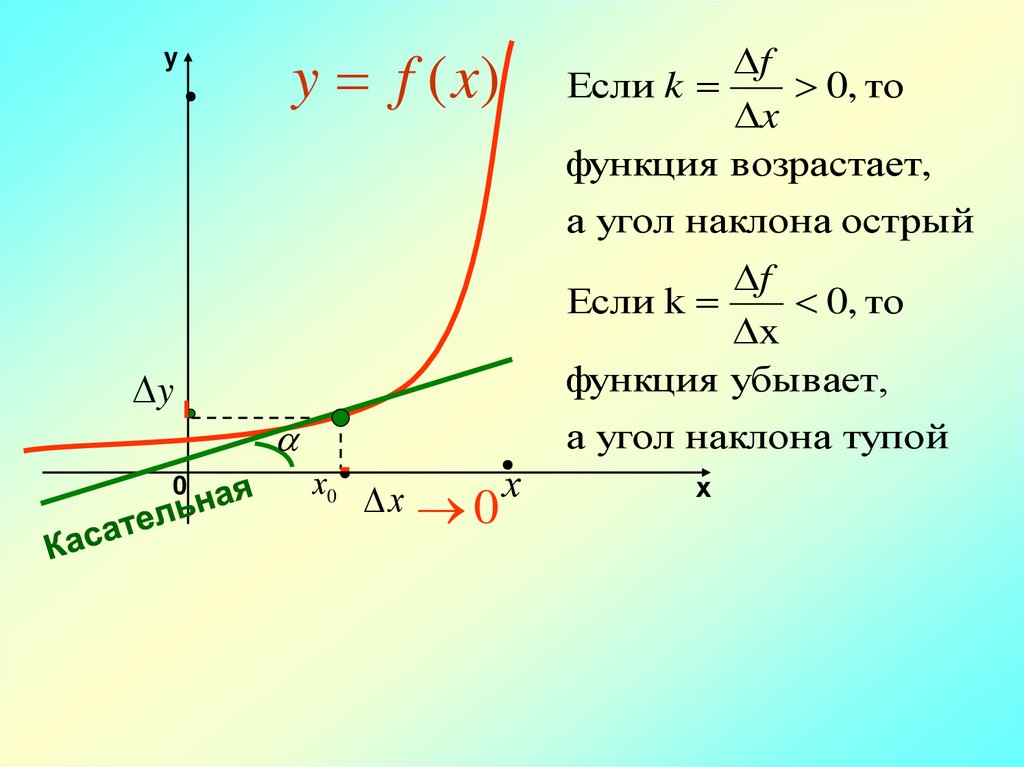
yf
Если k
0, то
x
функция возрастает,
y f (x)
а угол наклона острый
f
Если k
0, то
x
функция убывает,
y
0
а угол наклона тупой
х0
х
0
х
х
10.
Алгоритм отыскания производнойдля функции, пользуясь её определением
1. Зафиксировать значение Х; найти f(x).
2.Дать аргументу Х приращение ∆Х, перейти в
новую точку Х+ ∆Х; найти f(x+∆x).
3.Найти приращение функции ∆f = f(x+∆x) - f(x).
4.Составить отношение ∆f/∆Х.
5.Вычислить предел этого отношения
f
f ( x) lim
x 0 x
/







 mathematics
mathematics








