Методы нулевого порядка. Метод Нелдера-Мида (деформируемого многогранника)

1. в) метод Нелдера-Мида (деформируемого многогранника)

В 1964 году Нелдер и Мид предложили
модификацию, в которой симплекс может
изменять свою форму (растягиваясь и
сжимаясь) в зависимости от свойств
поверхности целевой функции. Так как в
этом случае симплекс не будет уже
регулярным, метод назвали поиском по
деформируемому многограннику.

2.

Модифицируем рассмотренный в п.б
алгоритм минимизации целевой функции
по регулярному симплексу, добавив к
процедуре отражения при построении
нового симплекса процедуры сжатия и
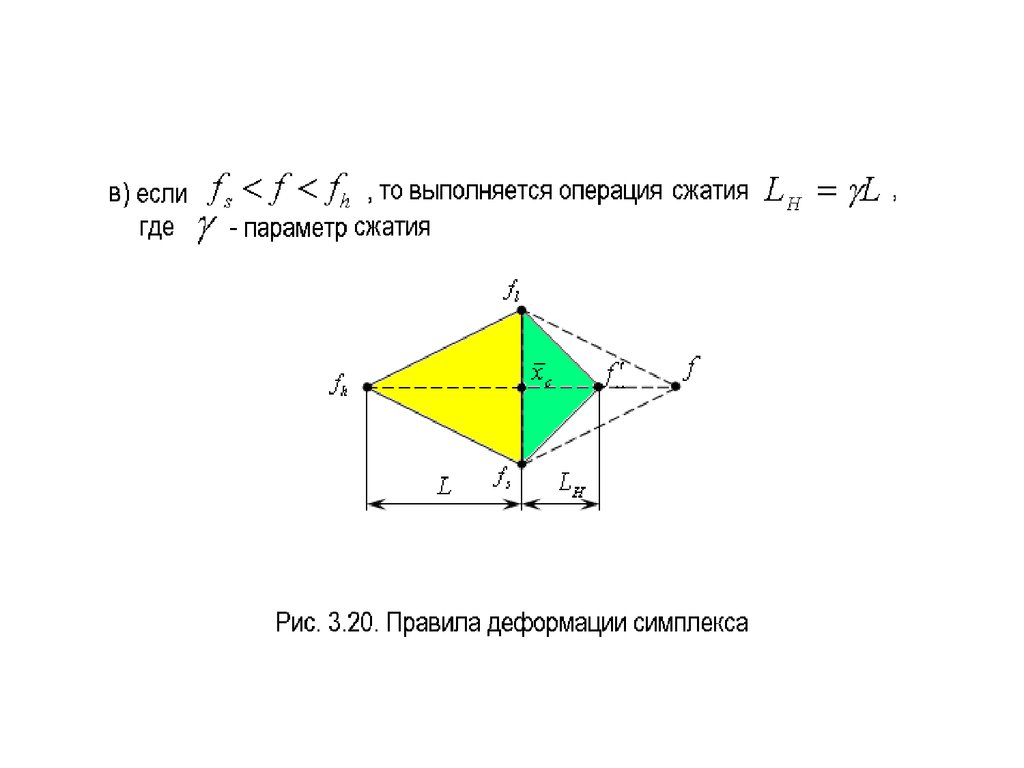
растяжения. Геометрическая иллюстрация
этих процедур для случая представлена
на рис. 3.20, где введены следующие
обозначения:

3.

f h - наибольшее значение целевой
функции;
f s - следующее по величине за
наибольшим значение целевой
функции;
f l - наименьшее значение целевой
функции;
/
f , f - текущие значения целевой
функции.

4.

5.

6.

При решении практически задач
минимизации параметры растяжения
и сжатия Нелдер и Мид рекомендует
брать 2 , 0,5 , Павиани – выбирать
эти параметры из интервалов
2,8 3,0 ;
0,4 0,6 .

7. Алгоритм поиска методом Нелдера-Мида

1. Задать размерность задачи оптимизации n ,
координаты начальной точки многогранника
x (0) ( x1(0) , x2(0) , , xn(0) ) , длину ребра многогранника
m, параметр растяжения , параметр сжатия
, точность поиска .
2. Построить начальный многогранник в виде
регулярного симплекса, вычисляя координаты
(1)
( 2)
(n)
x
,
x
,
,
x
остальных n вершин
по
формулам (3.22).

8.

3. Определить номер вершины k с наибольшим
(k )
f
f
(
x
),
значением целевой функции h
номер вершины k1 с наименьшим значением
( k1 )
целевой функции fl f ( x ) и номер
вершины k 2 - со следующим по величине за
наибольшим значением целевой функции
( k2 )
fs f (x ) .
4. Определить центр тяжести всех вершин
(k )
x
:
многогранника за исключением вершины
1 n (i )
xc x .
n i 0
i k

9.

(k )
5. Отразить вершину x относительно центра
(k )
тяжести x 2 xc x . Вычислить значение
целевой функции f (x) в отраженной точке и
перейти к пункту 6.
f ( x) f ( x (k ) ) ,
6. Проверить условие. Если
то
операция отражения закончилась успешно.
(k )
(k )
f
(
x
) f ( x) и перейти к
x
x
,
Положить
пункту 7. В противном случае перейти к пункту
9 и выполнить операцию сжатия.

10.

7. Проверить условие. Если f ( x ) f l , то
выполнить операцию растяжения
(k )
x xc ( x ( k ) xc ) ,
вычислить значение целевой функции f (x) и
перейти к пункту 8, иначе – к пункту 9.
(k )
f
(
x
)
f
(
x
) , то
8. Проверить условие. Если
операция растяжения закончилась успешно.
(k )
(k )
f
(
x
) f ( x) и перейти
Положить x x ,
к пункту 12, иначе – к пункту 9.

11.

9. Проверить условие. Если f s f ( x) f h , то
выполнить операцию сжатия
x xc ( x xc )
вычислить значение целевой функции f (x) и
перейти к пункту 10, иначе к пункту 11.
(k )
(k )
f
(
x
)
f
(
x
) , то
10. Проверить условие. Если
операция сжатия закончилась успешно.
(k )
(k )
Положить x x , f ( x ) f ( x) и перейти к
пункту 12, иначе к пункту 11.

12.

11. Выполнить операцию редукции. Для этого
определить номер вершины r с минимальным
(r )
f
f
(
x
).
значением целевой функции min
Используя соотношение
x (i ) x ( r ) 0,5 ( x (i ) x ( r ) ), i 0, n, i r
сформировать новый многогранник с
уменьшенными вдвое сторонами. Перейти к
шагу 12.

13.

12. Проверить критерий окончания процесса
поиска, предложенный Нелдером и Мидом
1
2
2
1 n
(i )
f ( x ) f ( xc ) ,
n 1 i 0
где
1 n (i )
xc
x
n 1 i 0
- центр тяжести
многогранника на
данном шаге.

14.

13. Если условие выполнено , то процесс
вычислений завершен. В качестве
приближенного решения принять вершину
многогранника с минимальным значением
целевой функции. В противном случае перейти
к шагу 3 и продолжить процесс итераций.

15.

Пример 3.9. Найти минимум целевой функции
f ( x) x12 x1 x2 3x22 x1
методом Нелдера-Мида с точностью 0,1.
Решение. Зададим начальную точку симплекса
x ( 0) ( x1( 0) , x2( 0) )T (0,0)T , длину ребра симплекса m 1 ,
параметр растяжения 2,8 , параметр сжатия 0,4.
Вычислим приращения
n 1 1
3 1
m
1 0,259 ;
1
2 2
n
2
n 1 n 1
3 2 1
m
1 0,966 .
2
n 2
2 2

16.

Используя 1 и 2 вычислим координаты двух
остальных вершин симплекса
x (1) ( x1( 0 ) 1 ; x2( 0 ) 2 )T
(0 0,259; 0 0,966)T (0,259; 0,966)T ;
x ( 2 ) ( x1( 0) 2 ; x2( 0) 1 )T
(0 0,966; 0 0,259)T (0,966; 0,259)T .

17.

Итерация 0. Вычислим значения целевой функции f (x)
(0)
(1)
( 2)
в вершинах x , x , x
и обозначим наибольшее
значение функции f h , следующее за наибольшим
значением f s , наименьшее значение функции f l .
( 2)
f
f
(
x
) 0,082 .
f s f ( x ) 0 , f h f ( x ) 2,357 , l
(0)
(1)
Наибольшее значение целевой функции соответствует
(1)
x
вершине
отразим ее относительно центра тяжести
(0)
( 2)
x
x
.
вершин
и
1 ( 0)
x c1 ( x1 x1( 2 ) ; x2( 0 ) x2( 2 ) )T (0,483; 0,129)T .
2

18.

Используя свойство регулярности, найдем координаты
отраженной вершины
x (3) 2 xc1 x (1)
2(0,483; 0,129)T (0,259; 0,966)T
(0,707; - 0,707)T . f ( x (3) ) 1,793.
Так как f ( x (3) ) f ( x (1) ) , то отражение удачно.
( 3)
f
(
x
) f l не выполняется.
Условие растяжения
Так как выполняется условие
f s 0 f ( x (3) ) 1,793 f h 2,357 ,
то выполним операцию сжатия симплекса

19.

x ( 4 ) x c1 0,4( x ( 3) x c1 )
(0,483; 0,129)T 0,4[(0,707; 0,707)T (0,483; 0,129)T ]
(0,573; 0,205)T .
( 3)
( 4)
f
(
x
)
f
(
x
) , то операция сжатия закончилась
Так как
удачно.
Следовательно текущий симплекс образован вершинами
x (0) ,
f ( x (0) ) 0 ,
( 2)
f
(
x
) 0,082 ,
x ,
( 2)
( 4)
x ,
f ( x ( 4) ) 0,001 .

20.

Проверим условие окончания поиска. Определим
координаты центра тяжести симплекса
1 (0)
xc ( x1 x1( 2 ) x1( 4 ) ; x2( 0 ) x2( 2 ) x2( 4 ) )
3
1
(0 0,966 0,573; 0 0,259 0,205)T (0,513; 0,018)T ,
3
f ( x c ) 0,258 .
Вычислим
1
2
2
1 2
(i )
f ( x ) f ( xc )
n 1 i 0
1
2
1
2
2
2
(0 0,258) ( 0,082 0,258) ( 0,001 0,258)
3
0,234

21.

Процесс итераций продолжается.
Итерация 1. Текущий симплекс образован вершинами
( 4)
(0)
( 2)
x
, которым соответствует значение целевой
x , x ,
Функции
( 0)
fh f (x ) 0 ,
f l f ( x ( 2) ) 0,082 ,
f s f ( x ( 4) ) 0,001 .
(0)
x
Отразим вершину
относительно центра тяжести
( 2)
x
вершин
и x ( 4)

22.

xc2
1 ( 2)
( 4)
( 2)
( 4) T
T
( x1 x1 ; x2 x2 ) (0,769; 0,027) .
2
Используя свойство регулярности, найдем координаты
отраженной вершины
x (5) 2 x c 2 x ( 0) 2 (0,769 ; 0,027)T (0; 0)T (1,539 ; 0,054)T ,
f ( x (5) ) 0,755 .
Так как
f ( x ( 0) ) f ( x (5) ) ,
то операция отражения
закончилась неудачей. Учитывая, что условие сжатия
(5)
f s f ( x ) f h также не выполнено, проведем
операцию редукции.

23.

Сформируем новый многогранник с уменьшенными
( 2)
вдвое сторонами и вершиной x , которой соответствует
( 2)
f
f
(
x
) 0,082
наименьшее значение целевой функции l
x ( 6 ) x ( 2) 0,5 ( x ( 0 ) x ( 2 ) )
(0,966 ; 0,259)T 0,5 (0 ; 0)T (0,966 ; 0,259)T
(0,483 ; 0,129)T ,
f ( x ( 6 ) ) 0,262,
x ( 7 ) x ( 2 ) 0,5 ( x ( 4 ) x ( 2 ) )
(0,966 ; 0,259)T 0,5 (0,573 ; - 0,205)T (0,966 ; 0,259)T
(0,769 ; 0,027)T ,
f ( x ( 7 ) ) 0,196.

24.

После операции редукции текущий многогранник
образован вершинами x ( 2 ) , x ( 6 ) , x ( 7 ) , которым
соответствует значение целевой функции
f ( x ( 2) ) 0,082 , f ( x ( 6) ) 0,262 , f ( x ( 7 ) ) 0,196 .
Проверим условие окончания поиска. Определим
координаты центра тяжести симплекса
1 ( 2)
xc ( x1 x1( 6 ) x1( 7 ) ; x2( 2 ) x2( 6 ) x2( 7 ) )
3
1
(0,966 0,483 0,769; 0,259 0,129 0,027)T
3
(0,739; 0,138)T ; f ( xc ) 0,238 .

25.

Вычислим
1
2
2
1 2
(i )
f ( x ) f ( xc )
n 1 i 0
1
2
1
( 0,082 0,238) 2 ( 0,262 0,238) 2 ( 0,196 0,238) 2
3
0,094 .
Так как условие окончания поиска выполняется, то
процесс итераций завершен.

26.

В качестве приближенного значения выбирается
вершина с наименьшим значением целевой
функции текущего симплекса, образованного
( 2)
(6)
(7)
вершинами x , x , x :
x* x ( 6 ) (0,438; 0,129)T ,
f ( x* ) 0,262 .