Similar presentations:
Решение квадратных неравенств. 8 класс
1.
Решениеквадратных
неравенств
Алгебра
8 класс
УРОКИ
3-4
2. Дата: 29.04.20 Тема урока: «Графический метод решения квадратных неравенств».
3.
Повторение1.Какое неравенство называется
квадратным?
№1.
Из приведенных неравенств выберите неравенства
второй степени?
4.
Проверь себя!1. Квадратным называется неравенство, левая часть которого
−квадратный трёхчлен, а правая часть равна нулю.
№1.
Из приведенных неравенств квадратными
являются неравенства:
5.
2. Что зависит от знака первого коэффициентаквадратичной функции?
3. Как знак дискриминанта влияет на
количество точек пересечения графика
квадратичной функции с осью ОХ?
4. Как ещё называют точки пересечения
графика функции с осью ОХ?
6.
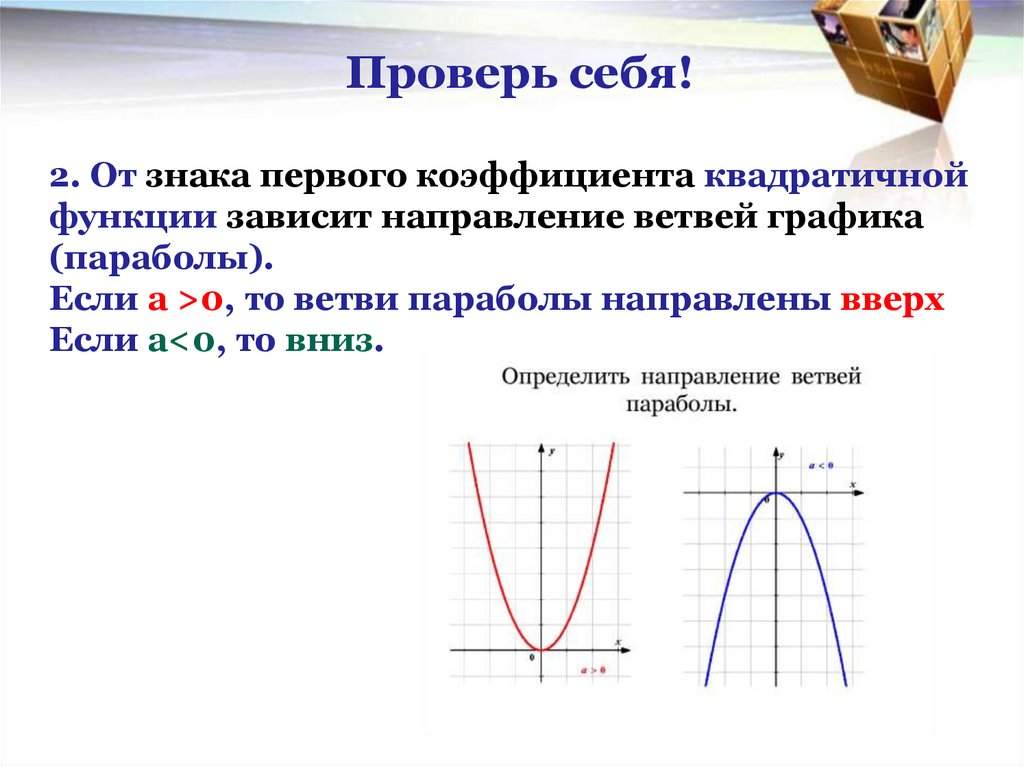
Проверь себя!2. От знака первого коэффициента квадратичной
функции зависит направление ветвей графика
(параболы).
Если а >0, то ветви параболы направлены вверх
Если а<0, то вниз.
7.
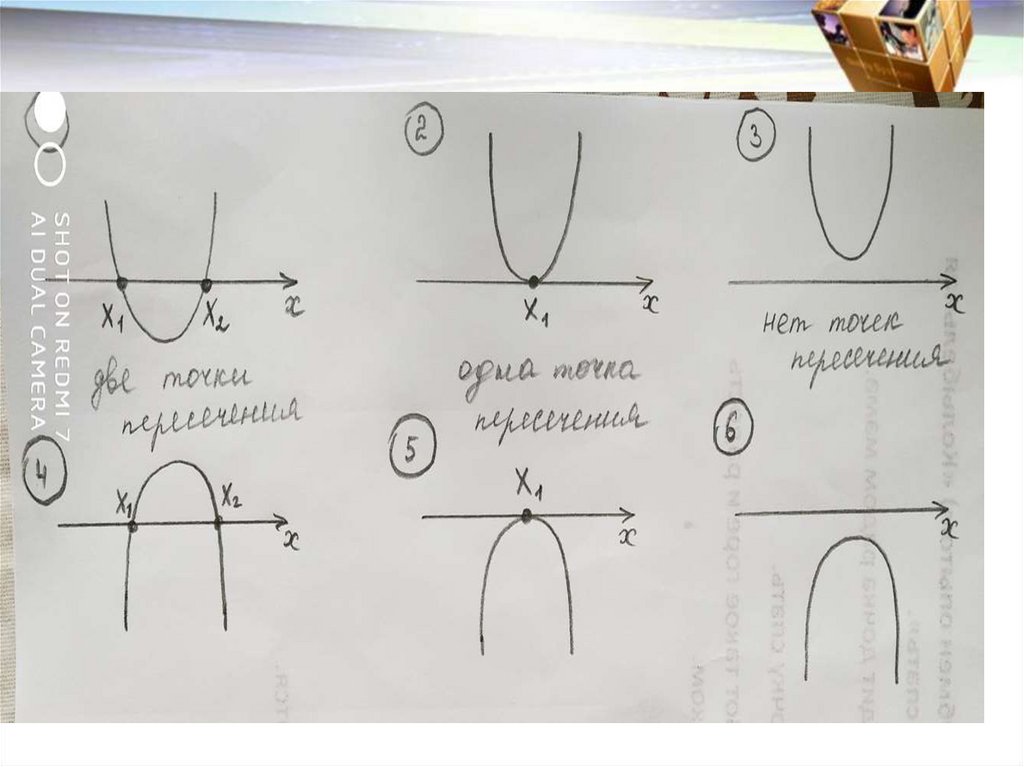
3. От знака дискриминанта зависит количествоточек пересечения графика квадратичной
функции с осью ОХ (т.е. количество корней
соответствующего квадратного уравнения).
• Если D>0, то график квадратичной функции
имеет 2 точки пересечения с осью Ох
(2 корня у уравнения).
• Если D=0, то график квадратичной функции
имеет 1 точку пересечения с осью Ох
(1 корень у уравнения).
• Если D<0, то график квадратичной функции
не имеет точек пересечения с осью Ох
(нет корней у уравнения).
4. Точки пересечения графика функции с осью
Ох называют нулями функции.
8.
9.
№2.Назовите число корней уравнения
и знак коэффициента
, если график
соответствующей квадратичной функции
расположен следующим образом:
1)
2)
3)
4)
5)
6)
10.
ПРОВЕРЬ СЕБЯ!№2.
1) a>0,D>0 (2 корня).
2) a<0, D>0(2 корня).
4) a<0,
D=0 (1 корень).
5) a>0, D<0
(нет корней).
3) a<0,
D<0 (нет корней).
6) a>0,
D=0 (1 корень).
11.
5. Что называют промежуткомзнакопостоянства функции?
6. Как на графике определить промежуток
знакопостоянства функции?
1)
2)
3)
12.
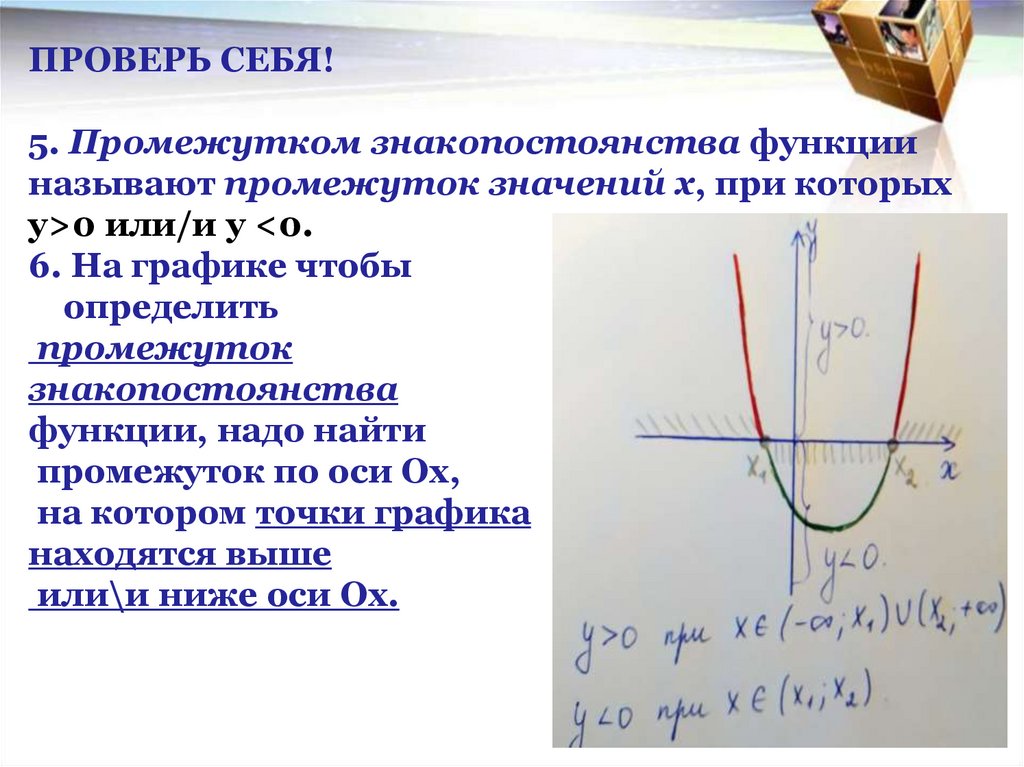
ПРОВЕРЬ СЕБЯ!5. Промежутком знакопостоянства функции
называют промежуток значений х, при которых
у>0 или/и у <0.
6. На графике чтобы
определить
промежуток
знакопостоянства
функции, надо найти
промежуток по оси Ох,
на котором точки графика
находятся выше
или\и ниже оси Ох.
13.
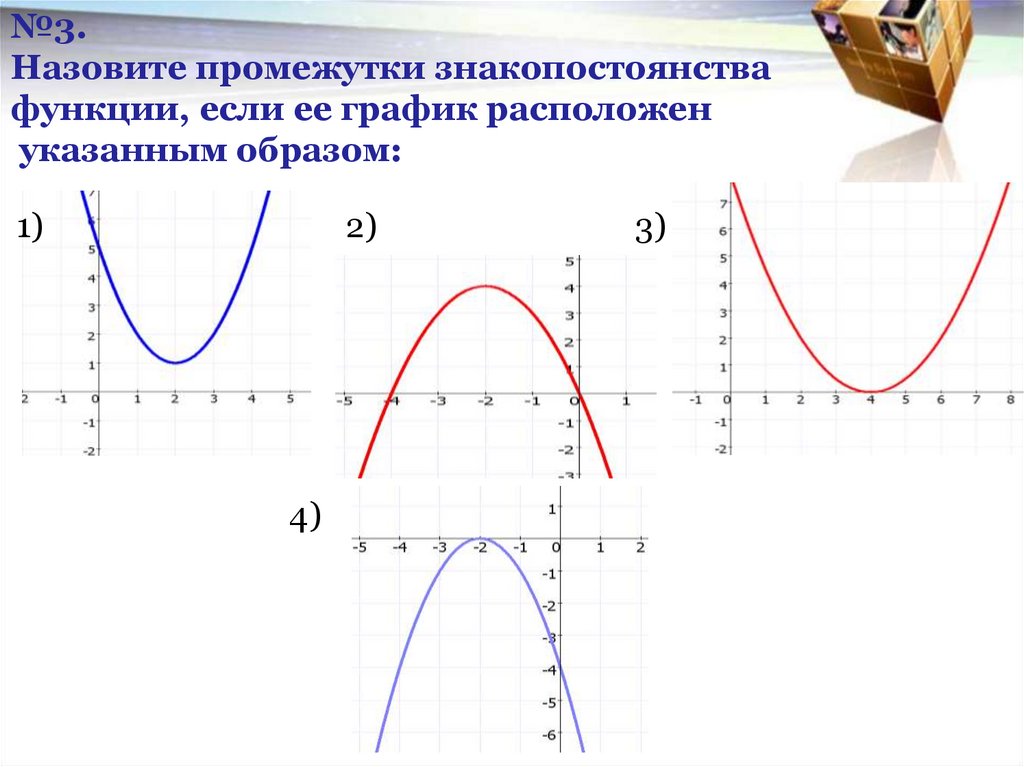
№3.Назовите промежутки знакопостоянства
функции, если ее график расположен
указанным образом:
1)
2)
4)
3)
14.
ПРОВЕРЬ СЕБЯ!№3.
1) у>0 при любом х 2) у>0 при -4<х<0;
3) у>0 при любом х,
Y<0 при х<-4 и х>0.
кроме х=4
4)у<0 при любом х,
кроме х=-2.
15. Графический метод решения квадратного неравенства:
1).Определить направление ветвейпараболы, по знаку первого коэффициента
квадратичной функции.
2). Найти корни соответствующего
квадратного уравнения;
3). Построить эскиз графика и по нему
определить промежутки, на которых
квадратичная функция принимает
положительные или отрицательные
значения (всё зависит от знака
неравенства, которое вы решаете)
16.
4) ПО ГРАФИКУ ОПРЕДЕЛИТЬ ПРОМЕЖУТКИ, НАКОТОРЫХ ФУНКЦИЯ ПРИНИМАЕТ НУЖНЫЕ
ЗНАЧЕНИЯ
2) РЕШИТЬ КВАДРАТНОЕ УРАВНЕНИЕ (если возможно)
3) СХЕМАТИЧНО ПОСТРОИТЬ ГРАФИК ДАННОЙ
ФУНКЦИИ
1) РАССМОТРЕТЬ ФУНКЦИЮ
5) ЗАПИСАТЬ ОТВЕТ
17. При решении квадратного неравенства графическим методом важно учитывать:
1)Порядок расположения корнейсоответствующего квадратного уравнения на
числовой прямой точками;
(если неравенство строгое, то точки выколоты,
если нестрогое, то закрашены)
2)направление ветвей параболы (по знаку
первого коэффициента квадратичной функции);
3) знак неравенства, которое решаете
(если у>0, то часть графика, которая выше оси
Ох, если у<0, то часть графика, которая ниже
оси Ох);
4) При записи ответа написание скобок:(если
строгое) ; [если неравенство нестрогое ].
18. Например:
Решить графически неравенствох²+5х-6≤0
Решение: рассмотрим функцию у = х²+5х-6,
это квадратичная функция, графиком является
парабола, т.к. а=1, то ветви направлены вверх.
у
+
+
-6
1
x
Ответ: [-6;1]
19.
№4. (Решения отправляем в ЛС)Из таблицы 1 выберите одну графическую
интерпретацию для каждого из неравенств 1- 4
Выберите из таблицы 1 графическую
интерпретацию для каждого из неравенств 1-4:
1)
1.
2) x 2 5 x 6 0.
2.
2
x
3) 5 x 6 0.
3.
4.
x 2 7 x 12 0.
4)2
x 6 x 9 0.
а
в
////// //////
3
x
с
//////
6
Таблица 1
1
x
//////
2 3
d
x
//////
2
//////
3 x
e
/////
2
///// //////
3 x
3
f
//////
4 x
20.
№5. (Решения отправляем в ЛС)таблице2 2найдите
найдитеверное
верноерешение
решениенеравенства
неравенства1,
ВВтаблице
, в таблице
3 - решение
неравенства
в1таблице
3 – решение
неравенства
2 . 2:
1. x 2
1)
3x 4 0
x 3x 10 0.
2.
2
2)
Таблица 2
а
в
x 1;4 x ; 1 4;
с
d
x 1;4 x ; 1 4;
Таблица 3
а
в
x 2;5 x ; 2 5;
с
d
x 2;5 x ; 2 5;
















 mathematics
mathematics








