Расчет распределения пор по размерам из изотерм адсорбции

1. Расчет распределения пор по размерам из изотерм адсорбции

Рассмотрены методы расчета распределения объема пор* по характерным размерам,
включая традиционные методы, основанные на макроскопической термодинамике
(уравнение Кельвина и зависимость t(P/P0))
и новые численные методы, базирующиеся
модельных потенциалах взаимодействия и
статистической термодинамике флюидов
(газов и жидкостей).
*Далее для краткости- PSD- pore size distribution
1

2.

Типовая изотерма адсорбции на материале с
микро- и мезопорами и ее анализ
традиционными методами
Полимолекулярная ад-
а
сорбция в макропорах
Область
капиллярной
конденсации
в мезопорах
Р/Р0
Расчет распределения
мезопор на основе
уравнения Кельвина
1.0
Область моно- и полимолекулярной адсорбции,
заполнение микропор
Расчеты удельной
поверхности и микро2
пористости

3. заполнения/освобождения капилляра постоянного сечения с дном и без дна (прямой цилиндр)

Цилиндр
с дном без дна
C
A
В
D
При постоянстве кривизны
профиля мениска капилляр
спонтанно заполняется при
конденсации или освобождается
при десорбции при относительном
давлении
Р = Р0 ехр(-2 пж Vm/rkRT) (уравнение Кельвина)
rk=r-t(P/P0)
С дном rk=r-t(P/P0)-сферич мениск; без дна rk=2(r-t(P/P0))-цилиндрич.
3

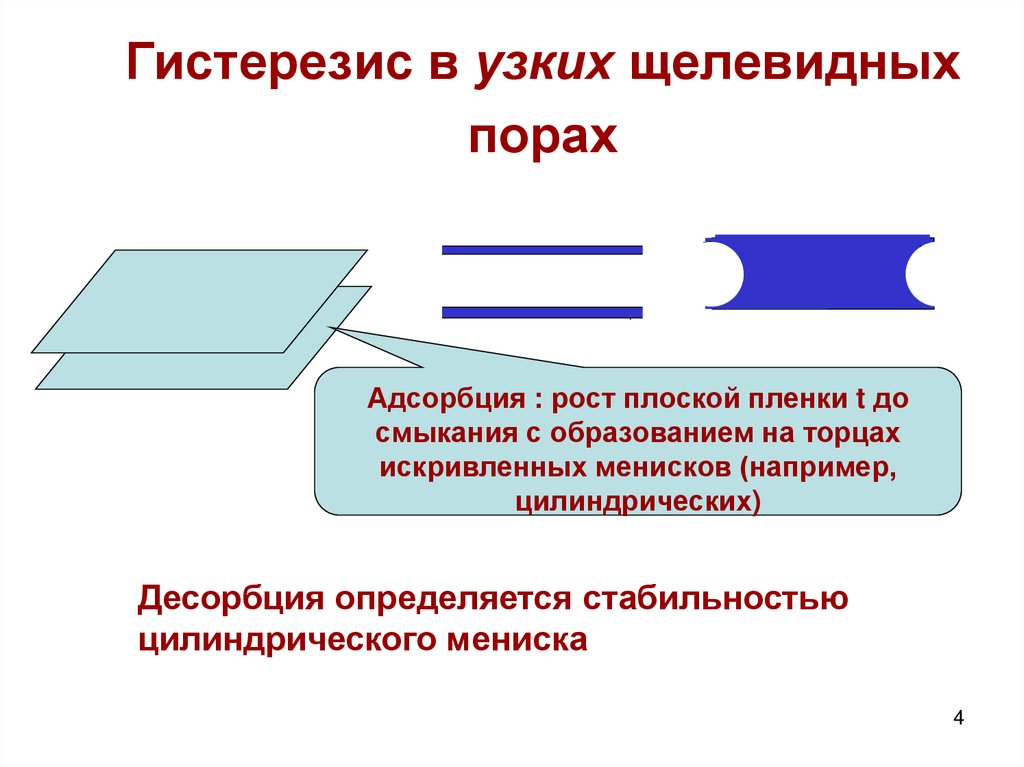
4. Гистерезис в узких щелевидных порах

Адсорбция : рост плоской пленки t до
смыкания с образованием на торцах
искривленных менисков (например,
цилиндрических)
Десорбция определяется стабильностью
цилиндрического мениска
4

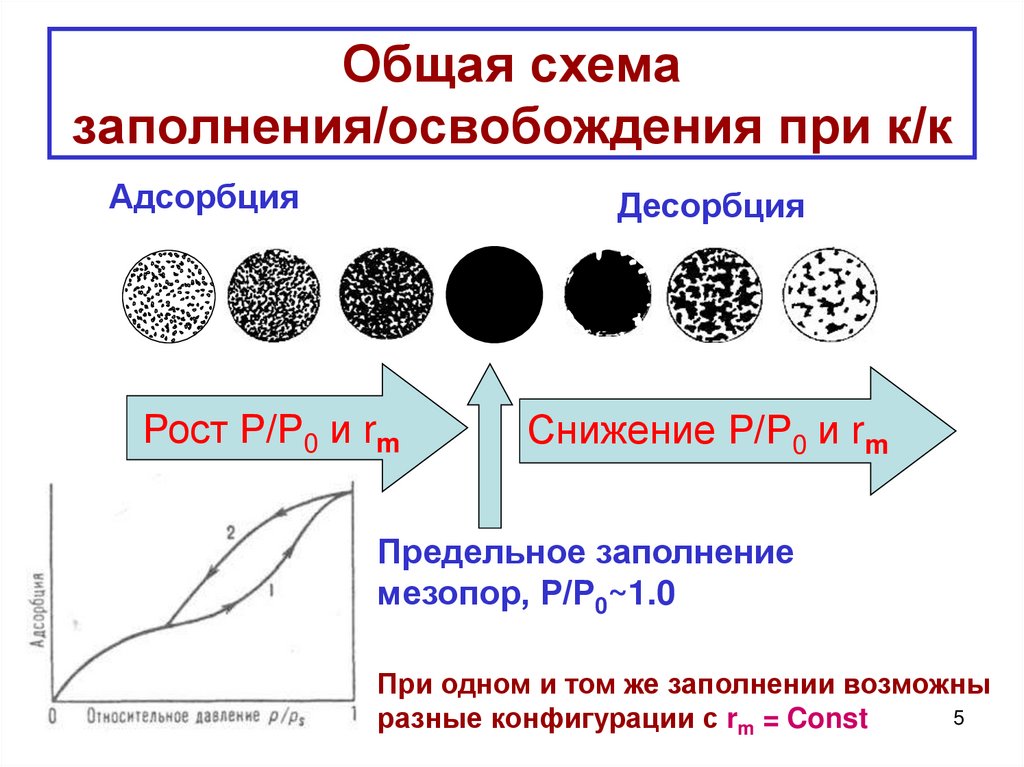
5. Общая схема заполнения/освобождения при к/к

Адсорбция
Десорбция
Рост Р/Р0 и rm
Снижение Р/Р0 и rm
Предельное заполнение
мезопор, Р/Р0~1.0
При одном и том же заполнении возможны
5
разные конфигурации с rm = Const

6. О моделировании процессов к/к

Сложность реальных процессов, происходящих при капиллярной конденсации,
приводит к необходимости моделирования:
замены реальной сложной структуры
упрощенной геометрической моделью с
простой формой пор и эквивалентной
формой петли гистерезиса. Эквивалентный
адсорбент имеет тот же суммарный объем
пор и суммарную удельную поверхность,
близкую к измеренной независимыми
методами.
6

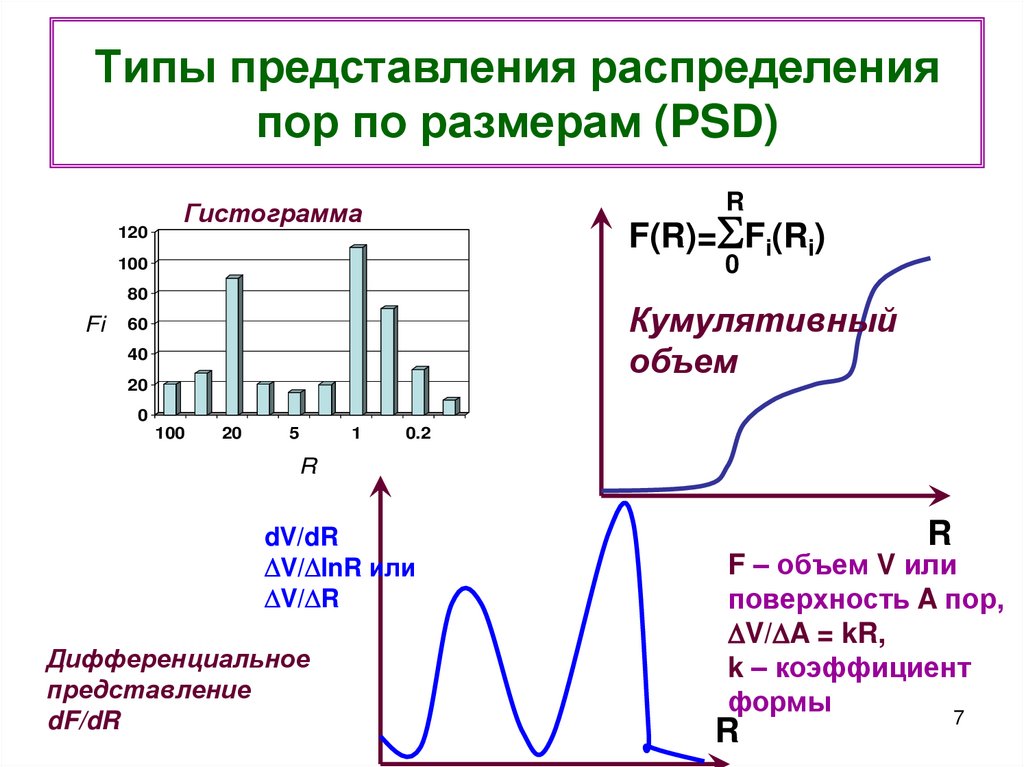
7. Типы представления распределения пор по размерам (PSD)

120
R
Гистограмма
F(R)= Fi(Ri)
0
100
80
Fi
Кумулятивный
объем
60
40
20
0
100
20
5
1
0.2
R
dV/dR
V/ lnR или
V/ R
Дифференциальное
представление
dF/dR
R
F – объем V или
поверхность A пор,
V/ A = kR,
k – коэффициент
формы
7
R

8.

-Все существующие в настоящее время
методы расчета PSD основаны на использовании простейших моделей пористого
пространства (поры в виде открытых или
закрытых с торца цилиндров, плоских щелей,
реже – сфер или промежутков в регулярных
упаковках сферических частиц), которые
заполняются при адсорбции и освобождаются при десорбции независимо.
-Поэтому фактически рассчитывается PSD
для «эквивалентной» модели пористой
структуры, идентичной по адсорбционному
поведению (чувствительному к размерам
пор) .
8

9. Традиционные методы, основанные на уравнении Кельвина

Расчет может проводиться по адсорбционной или десорбционной
ветви капиллярно-конденсационного гистерезиса и начинается от
предельного заполнения при значениях Р/Р0~1, максимально близких
единице, Принимается, что все мезопоры в этом исходном положении
заполнены.
При Р/Р0<1 мезопоры размера Rп < rк(Р/Р0) - t (Р/Р0) заполнены, в порах
большего размера – только полимолекулярная пленка на поверхности.
Функция t (Р/Р0) задается интерполяционными уравнениями типа
t =b/ln(P/P0)3 (ФХХ) или более сложными полиномами, описывающими
стандартные ИА на непористой поверхности
Рассмотрим принципиальные особенности методики
расчета на примере модели десорбции из системы
цилиндрических пор с открытыми торцами.
В этом случае десорбция определяется кривизной
сферических менисков на торцах заполненных пор.
9

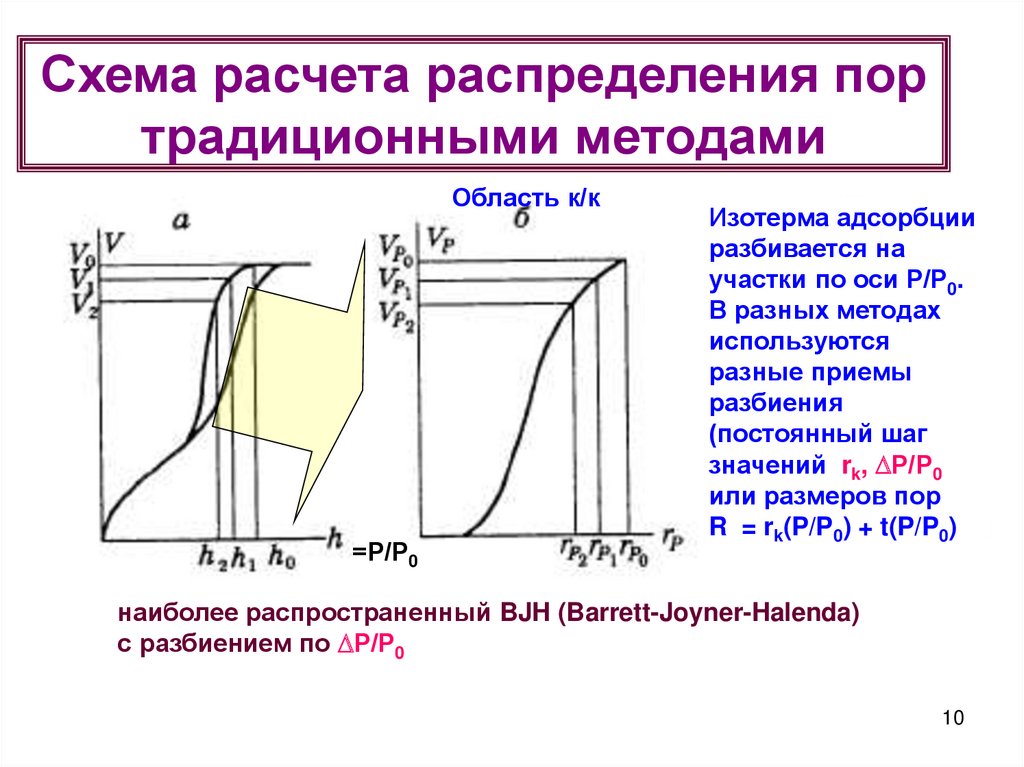
10.

Схема расчета распределения пор
традиционными методами
Область к/к
=Р/Р0
Изотерма адсорбции
разбивается на
участки по оси Р/Р0.
В разных методах
используются
разные приемы
разбиения
(постоянный шаг
значений rk, Р/Р0
или размеров пор
R = rk(P/P0) + t(P/P0)
наиболее распространенный BJH (Barrett-Joyner-Halenda)
с разбиением по Р/Р0
10

11.

Схема расчета распределения пор традиционными
методами по десорбц. ветви ИА
V1
V0
V1
V2 V3
R1
R2
V4
R3 R
4
Исходная
ситуация: все
поры заполнены
=Р/Р0
На их поверхности
осталась адс пленка
Первый шаг: (разница V0-V1)
освободились поры
размера R1 = rk(P/P0) + t (P/P0)
1 шаг
t(P/P0)
По этим результатам рассчитывается полный объем
освободившихся пор V1 и их поверхность А1
rк = R1 - t (P/P0)
11
R1

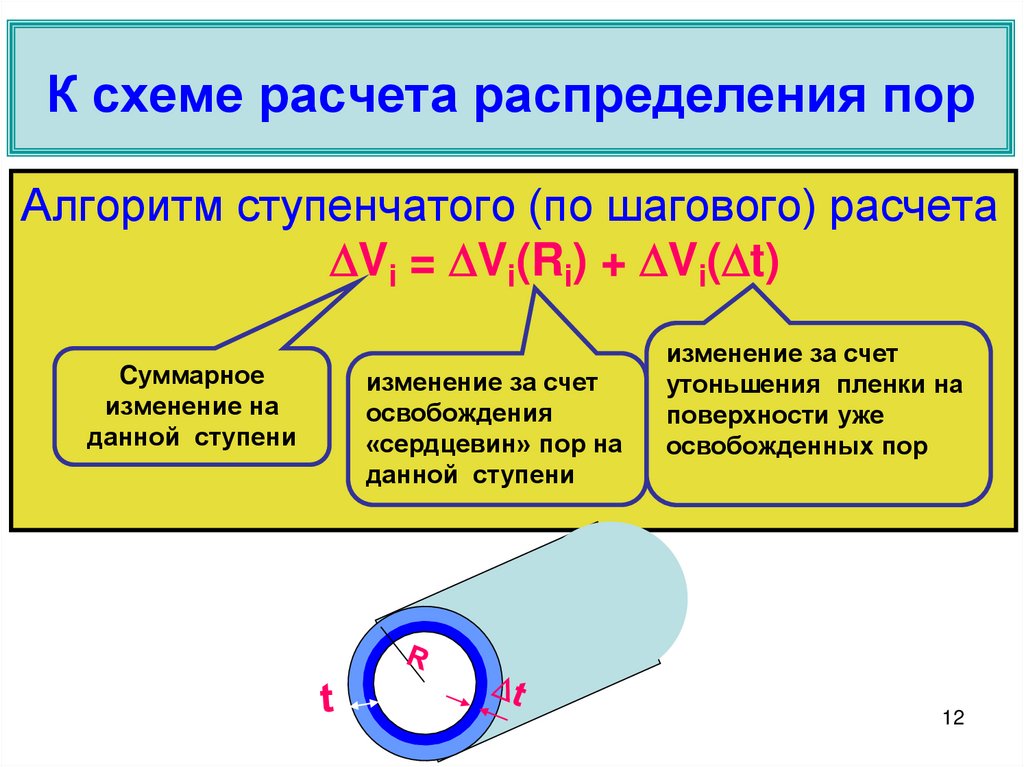
12. К схеме расчета распределения пор

Алгоритм ступенчатого (по шагового) расчета
Vi = Vi(Ri) + Vi( t)
Cуммарное
изменение на
данной ступени
изменение за счет
освобождения
«сердцевин» пор на
данной ступени
изменение за счет
утоньшения пленки на
поверхности уже
освобожденных пор
12

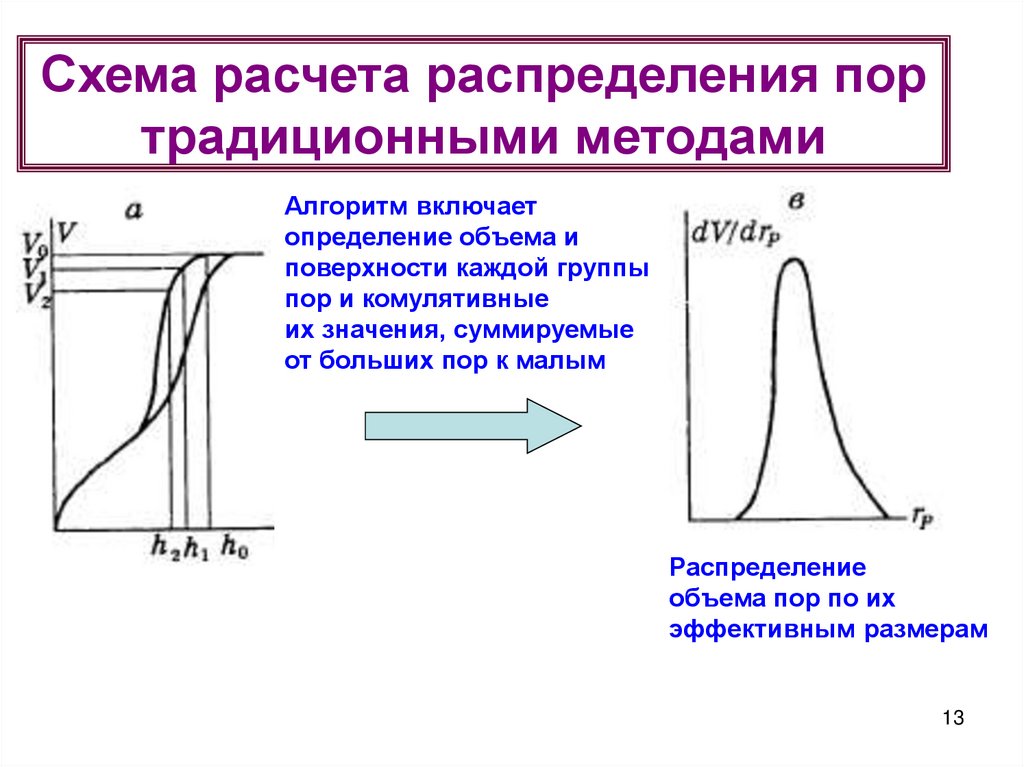
13.

Схема расчета распределения пор
традиционными методами
Алгоритм включает
определение объема и
поверхности каждой группы
пор и комулятивные
их значения, суммируемые
от больших пор к малым
=Р/Р0
Распределение
объема пор по их
эффективным размерам
13

14. Стандартное представление результатов расчета распределения пор по измерениям на ASAP-2400

P/P0
диапазон
диаметров
пор Средний
Результаты расчета
по адс или десорбц ветвям
диаметр
Приращение
объема, Vi см3/г
комулятивный
объем, Vi см3/г
Приращение
поверхности, Ai м2/г
Комулятивная поверхность
комулятивная
мезопор обычно на 10-30% и более
2/г
поверхность,
A
м
i
отличается от независимо измеренной
14

15.

Интерпретация результатов
расчета распределения пор
Расчет по десорбционной
ветви –
распределение объема по
критическим размерам горл
Расчет по адсорбционной
ветви –
распределение объема
по размерам полостей
Механическая смесь двух силикагелей
15

16. Недостатки традиционных методов расчета распределения на основе уравнения Кельвина

а) использование законов макроскопической термодинамики и
эмпирических соотношений (для t(P/P0);
b) допущения о сохранении значений жп и vm в области
больших кривизн и малых t(P/P0);
c) ограниченное число доступных геометрических моделей с
простейшей формой менисков на поверхности ж/п;
d) невозможность расчетов распределения микро- и мезопор
в рамках одного метода (при некоторой условности границы
между микро- и мезопорами) – проблема стыковки
результатов независимых измерений.
16

17. Недостатки традиционных методов расчета распределения на основе уравнения Кельвина

Часть этих недостатков позволяют устранить
современные численные методы, в которых
условие заполнения по уравнению Кельвина
заменяется на условие, основанное на расчете
потенциалов межмолекулярного
взаимодействия адсорбат/адсорбент и
адсорбат/адсорбат в порах заданной формы.
Это позволяет проводить расчеты адсорбции как в
микро, так и мезопорах, при необходимости
рассчитывать значения жп, vm, теплоты адсорбции и
другие термодинамические характеристики.
17

18. Современные численные методы

Суммарная ИА представляется в виде
(Р,X) = (Р, X) f(X) dX
где f(Xi) плотность распределения участков c
разными характерными размерами Х,
который в общем случае охватывает как
микро- так и мезопоры.
Функция (Р,Х) ( или (Р, U)) не задается
уравнением Кельвина, ТОЗМ, Ленгмюра и т.д.
а рассчитывается для модельных пор
заданной геометрии с использованием
модельных потенциалов межмолекулярных
взаимодействий.
18

19.

(Р,Х.) = (Р, Х) f(Х) dХ
Плотность распределения f(Х)
подбирается стыковкой с
экспериментом или задается
достаточно универсальными
модельными функциями, например,
как сумма нескольких логнормальных
распределений, константы которых
определяются численными методами
стыковкой с экспериментом.
19

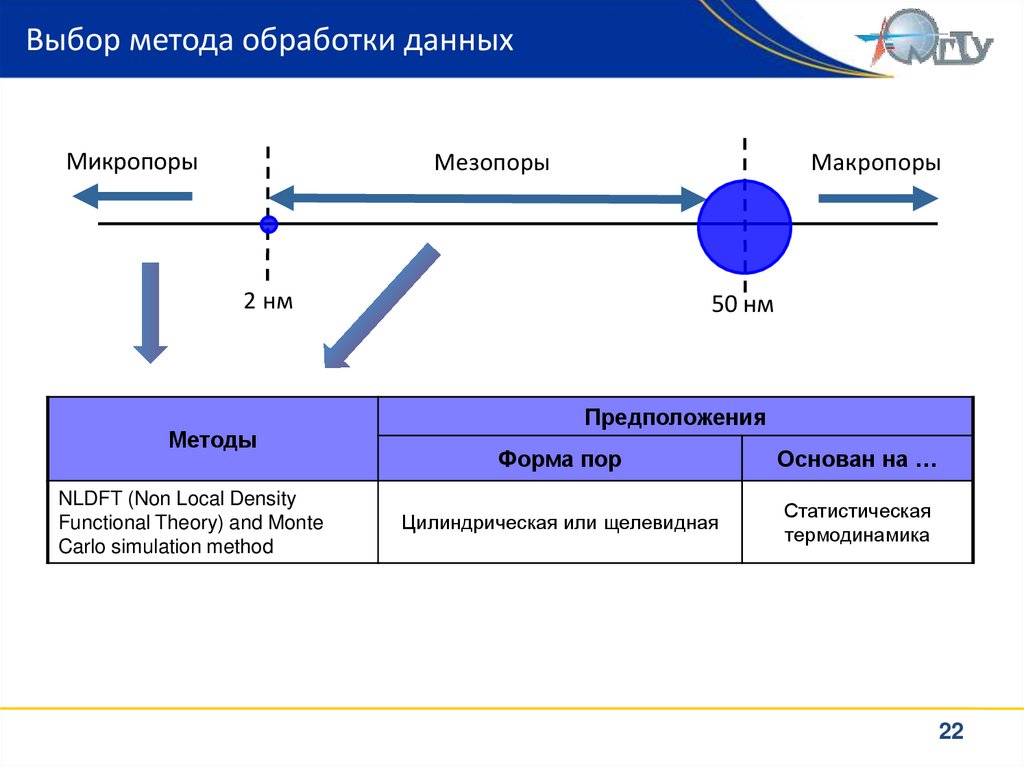
20. Выбор метода обработки данных

Микропоры
Мезопоры
Макропоры
2 нм
Методы
Brunauer method (для микропор)
50 нм
Предположения
Форма пор
Основан на …
Цилиндрическая или щелевидная
t-метод де Бура
•Теория адсорбции
Dubinin-Astakhov method
-
Поляни
•Распределение
Вейбула (или Гаусса)
•Модифицированное
HK (Horvath-Kawazoe) method
Saito-Foley method
Щелевидная
Цилиндрическая
уравнение ЮнгаЛапласа
•Распределение
Вейбула (или Гаусса)
HK method
20

21. Выбор метода обработки данных

Микропоры
Мезопоры
Макропоры
2 нм
Методы
BJH (Barrett, Joyner and Halenda)
method
DH (Dollimore Heal) method
50 нм
Предположения
Форма пор
Основан на …
Цилиндрическая или щелевидная
Уравнение Кельвина
Цилиндрическая
t-метод де Бура
21

22. Выбор метода обработки данных

Микропоры
Мезопоры
Макропоры
2 нм
Методы
NLDFT (Non Local Density
Functional Theory) and Monte
Carlo simulation method
50 нм
Предположения
Форма пор
Основан на …
Цилиндрическая или щелевидная
Статистическая
термодинамика
22