Теория множеств

1. Основы математической обработки информации

ОСНОВЫ МАТЕМАТИЧЕСКОЙ
ОБРАБОТКИ ИНФОРМАЦИИ
Преподаватель:
Плеханова Мария Валерьевна
ауд. 211, 303

2. Лекция 1 Теория множеств

ЛЕКЦИЯ 1
ТЕОРИЯ МНОЖЕСТВ

3. Георг Кантор (1845 - 1918)

ГЕОРГ КАНТОР (1845 - 1918)
немецкий математик,
логик, теолог,
основоположник теории
множеств.
«Множество есть
многое,
мыслимое нами
как единое»

4. Понятие множества

ПОНЯТИЕ МНОЖЕСТВА
Множество – это совокупность различимых
между собой объектов, объединяемых в целое
некоторым общим признаком.
Объекты, из которых состоит
называются его элементами.
Обозначения:
A, B, C, … - множества,
а, b, c, … - элементы множества.
множество,

5. Определения, термины и символы

ОПРЕДЕЛЕНИЯ, ТЕРМИНЫ И СИМВОЛЫ
Принадлежность:
a A - элемент aпринадлежит
множеству A
a A - элемент
множеству
aне принадлежит
A

6. Определения, термины и символы

ОПРЕДЕЛЕНИЯ, ТЕРМИНЫ И СИМВОЛЫ
Множество, не содержащее ни одного
элемента, называется пустым множеством
и обозначается Ø.

7. Определения, термины и символы

ОПРЕДЕЛЕНИЯ, ТЕРМИНЫ И СИМВОЛЫ
Множество A называется подмножеством
множества B, если все элементы множества
A принадлежат и множеству B.
A B

8. Свойства подмножеств

СВОЙСТВА ПОДМНОЖЕСТВ
1. Пустое множество является подмножеством любого
множества.
2. Множество A является своим подмножеством,
т.е. A A .
(1) и (2) называют несобственными подмножествами.
4. Если
и
, то
.
B , то
A А – собственное
A B
5. Если A Bи
подмножество
.
B
A B AB, т.е.
A B

9. Примеры

ПРИМЕРЫ
1. Дано множество A 3, 8 , то его подмножества:
Ø, 3, 8 - несобственные подмножества,
3 , 8 - собственные подмножества.
2. Пусть A – множество четных чисел, B – множество
целых чисел, С – множество нечетных чисел. Тогда
A B
C B

10. Способы задания множеств

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ
1. Перечислением элементов множеств
A a1 , a2 , a3
A a1 , a2 , a3 , . . .
2. Указанием свойств элементов множества
A a | a простое число

11. Пример_1

ПРИМЕР_1
1.
Задать
перечислением
элементов
множество букв, составляющих слово
«СТАТИСТИКА»
A с, т, а, и , к

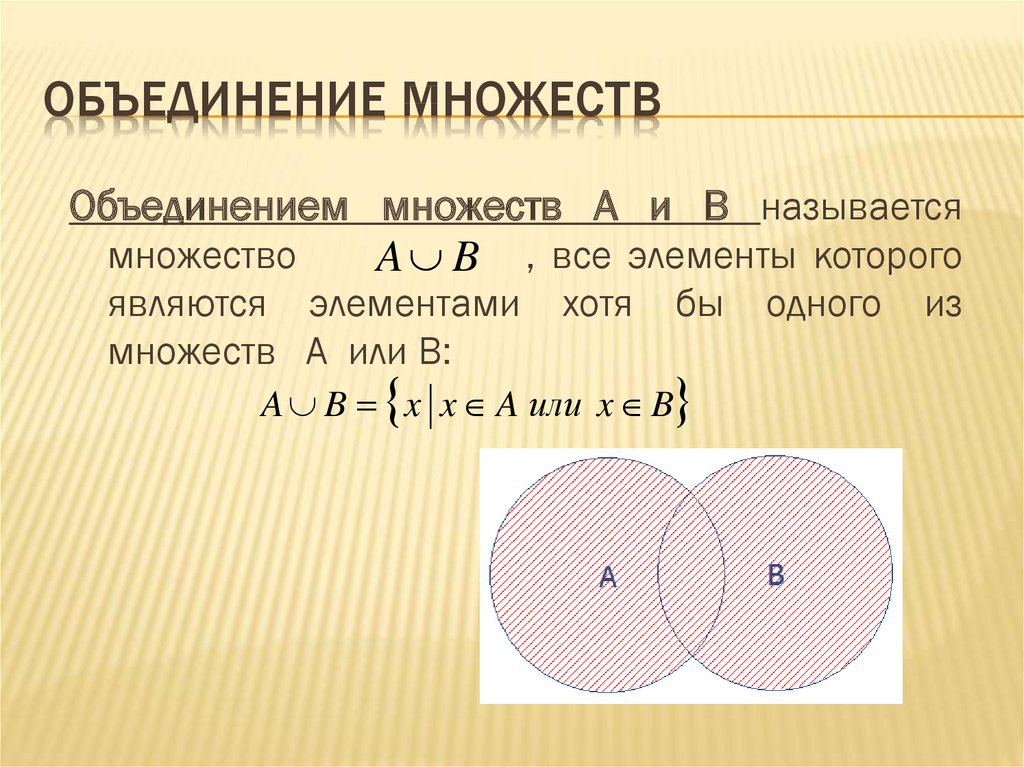
12. Объединение множеств

ОБЪЕДИНЕНИЕ МНОЖЕСТВ
Объединением множеств A и B называется
множество
A B , все элементы которого
являются элементами
множеств A или B:
хотя
бы
A B x x A или x B
одного
из

13. примеры

ПРИМЕРЫ
1. Пусть A 4, 5, 6,
Решение.
B 2, 4, .6 Найти
A . B
A B 2, 4, 5, 6
2. Пусть A – множество чисел, которые делятся на 2, а
В – множество чисел, которые делятся на 3.
Найти
.
Решение. A B
A 2, 4, 6, 8, 10, ...
B 3, 6, 9, 12, ...
A B 2, 3, 4, 6, 8, 9, 10, ...

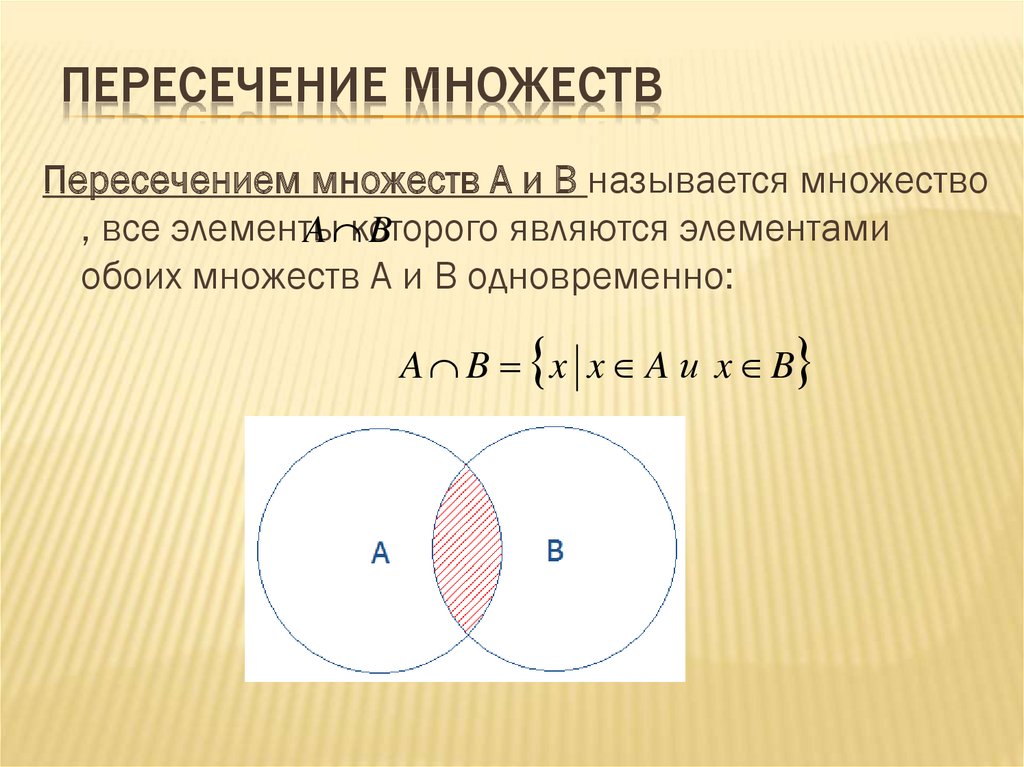
14. Пересечение множеств

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
Пересечением множеств A и B называется множество
, все элементы
являются элементами
A которого
B
обоих множеств A и B одновременно:
A B x x A и x B

15. примеры

ПРИМЕРЫ
A 4, 5, 6,
1. Пусть
Решение.
B 2, 4, .6 Найти
. B
A
A B 4, 6
2. Пусть A – множество чисел, которые делятся на 2, а
В – множество чисел, которые делятся на 3.
Найти
.
Решение. A B
A 2, 4, 6, 8, 10, ...
B 3, 6, 9, 12, ...
A B 6, 12, 18, ...

16. Примеры

ПРИМЕРЫ
3. Пусть A 1, 2 , B 2, 3 ,
Найти A B C .
Решение.
A B 2
A B C Ø
C 3, 4
.

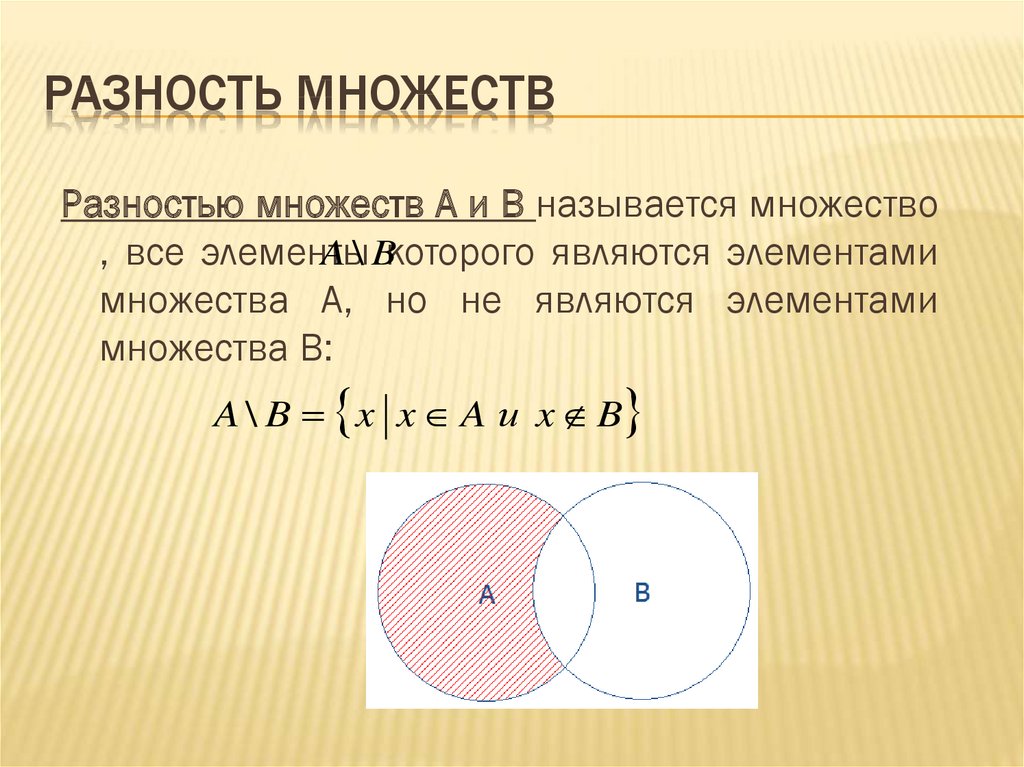
17. Разность множеств

РАЗНОСТЬ МНОЖЕСТВ
Разностью множеств A и B называется множество
A \ Bкоторого являются элементами
, все элементы
множества A, но не являются элементами
множества В:
A \ B x x A и x B

18. примеры

ПРИМЕРЫ
1. Пусть A 4, 5, 6,
Решение.
B 2, 4, .6 Найти
A, \ B
A \ B 5
.B \ A
B \ A 2чисел,
2. Пусть A – множество
которые делятся на 2, а
В – множество чисел, которые делятся на 3.
Найти
,
.
Решение.
A\ B B\ A
A 2, 4, 6, 8, 10, ...
B 3, 6, 9, 12, ...
A \ B 2, 4, 8, 10, 14, ...
B \ A 3, 9, 15, 21, ...

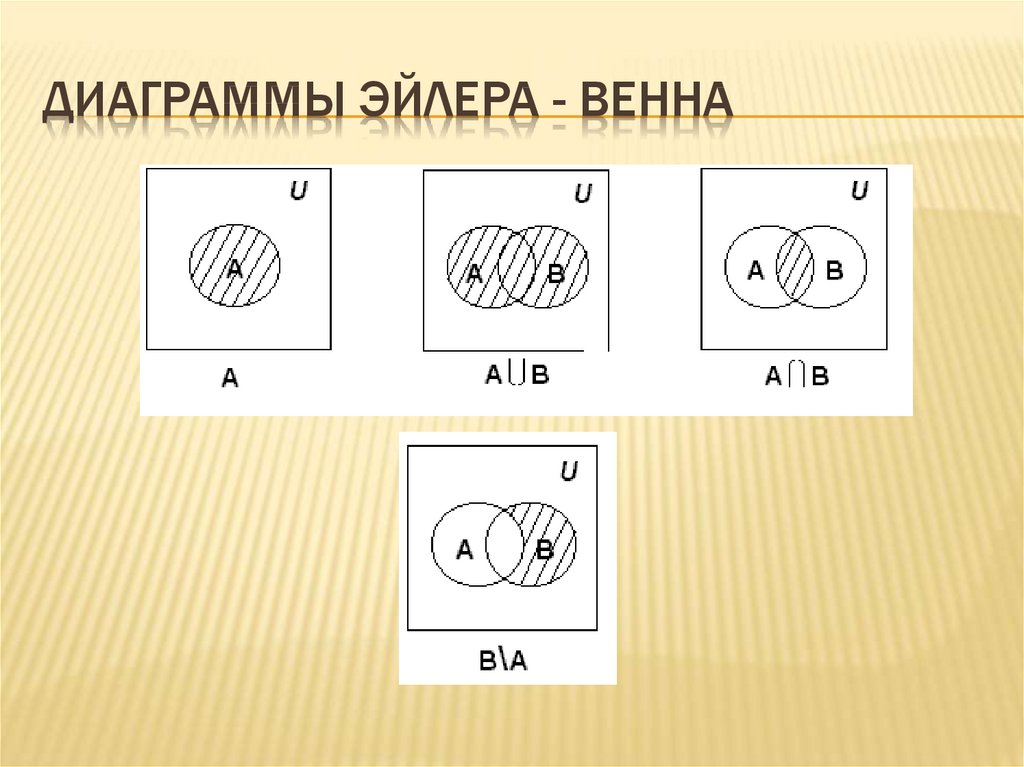
19. Диаграммы Эйлера - Венна

ДИАГРАММЫ ЭЙЛЕРА - ВЕННА

20. примеры

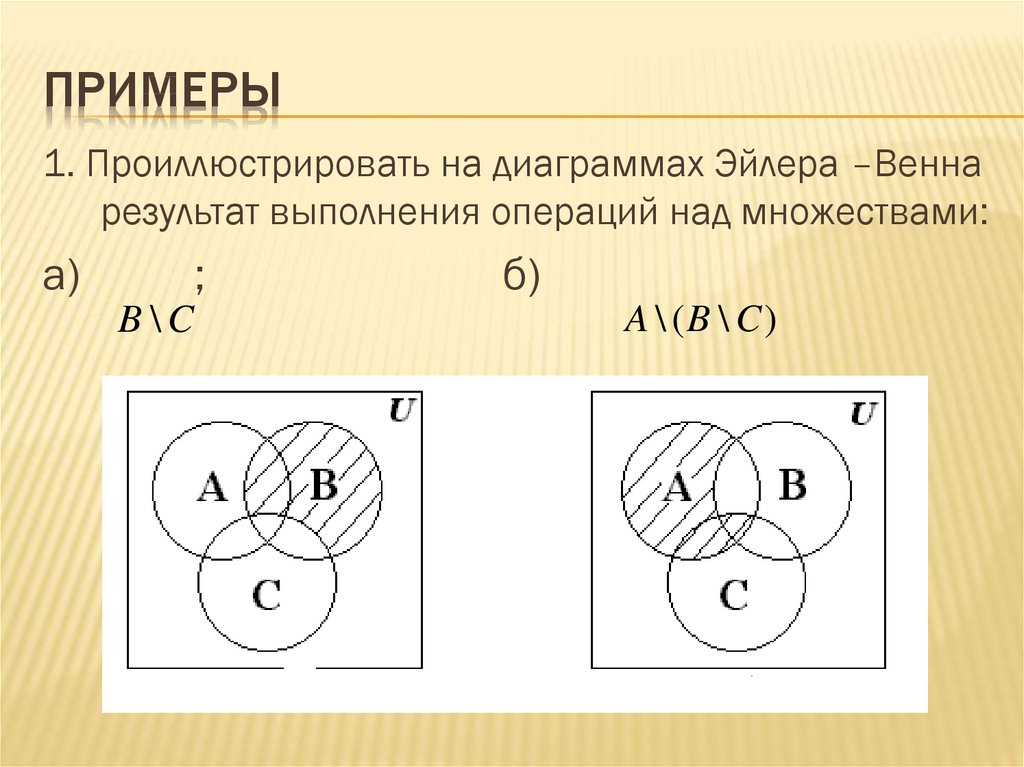
ПРИМЕРЫ
1. Проиллюстрировать на диаграммах Эйлера –Венна
результат выполнения операций над множествами:
а)
;
B\C
б)
A \ (B \ C)

21. примеры

ПРИМЕРЫ
1. Проиллюстрировать на диаграммах Эйлера –Венна
результат выполнения операций над множествами:
в)
A \;B
г)
A C

22. примеры

ПРИМЕРЫ
2. Каждый служащий агентства владеет хотя бы
одним иностранным языком: английским,
французским,
или
немецким.
Согласно
статистике, 17% служащих не знают английского
языка, 24% владеют английским и немецким
одновременно, 3% - всеми тремя языками, а
36% - только английским. Сколько процентов
служащих владеют английским и французским
языками одновременно?