Интеграл. Формула Ньютона – Лейбница

1. Интеграл. Формула Ньютона – Лейбница.

Занятие для 101 группы
Дата. 04 мая

2. Цель урока:

Ввести понятие интеграла и его вычисление по
формуле Ньютона – Лейбница, используя знания о
первообразной и правила её вычисления;
Проиллюстрировать практическое применение
интеграла на примерах нахождения площади
криволинейной трапеции;
Закрепить изученное в ходе выполнения
упражнений.

3.

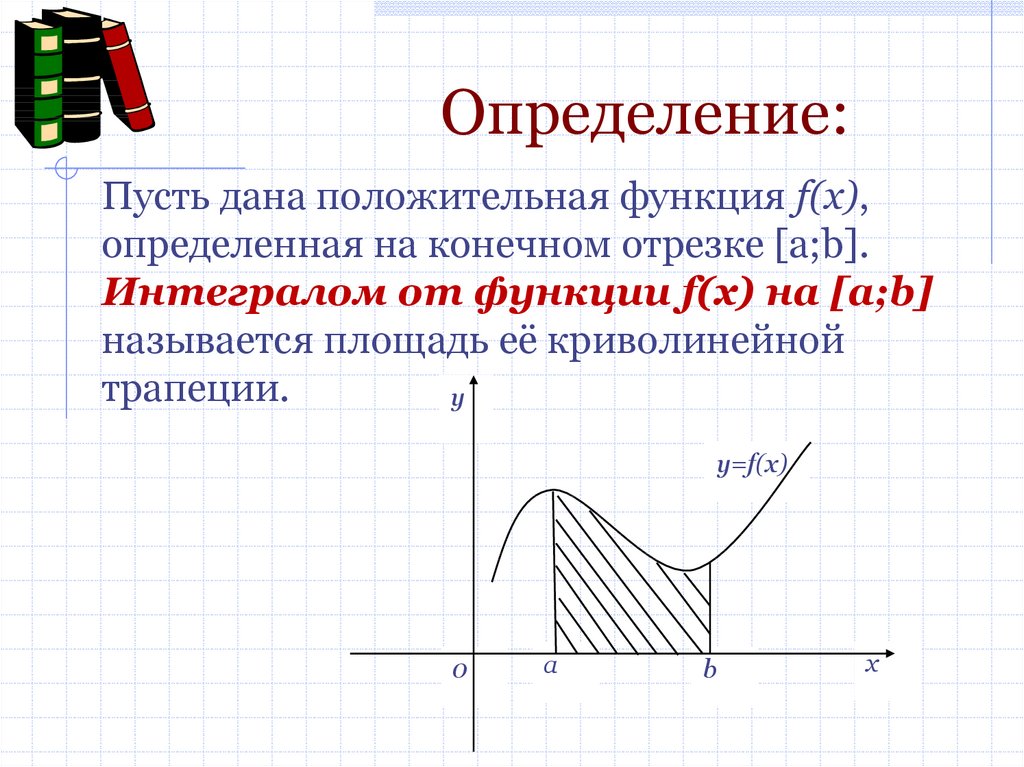
Определение:
Пусть дана положительная функция f(x),
определенная на конечном отрезке [a;b].
Интегралом от функции f(x) на [a;b]
называется площадь её криволинейной
трапеции.
y
y=f(x)
0
a
b
x

4. Обозначение:

«интеграл от a до b эф от икс дэ
икс»

5.

Формула Ньютона - Лейбница

6.

Пример 1.
Вычислить определённый интеграл:
Решение:
=

7.

Пример 2.
Вычислите определённые интегралы:
5
9
1

8.

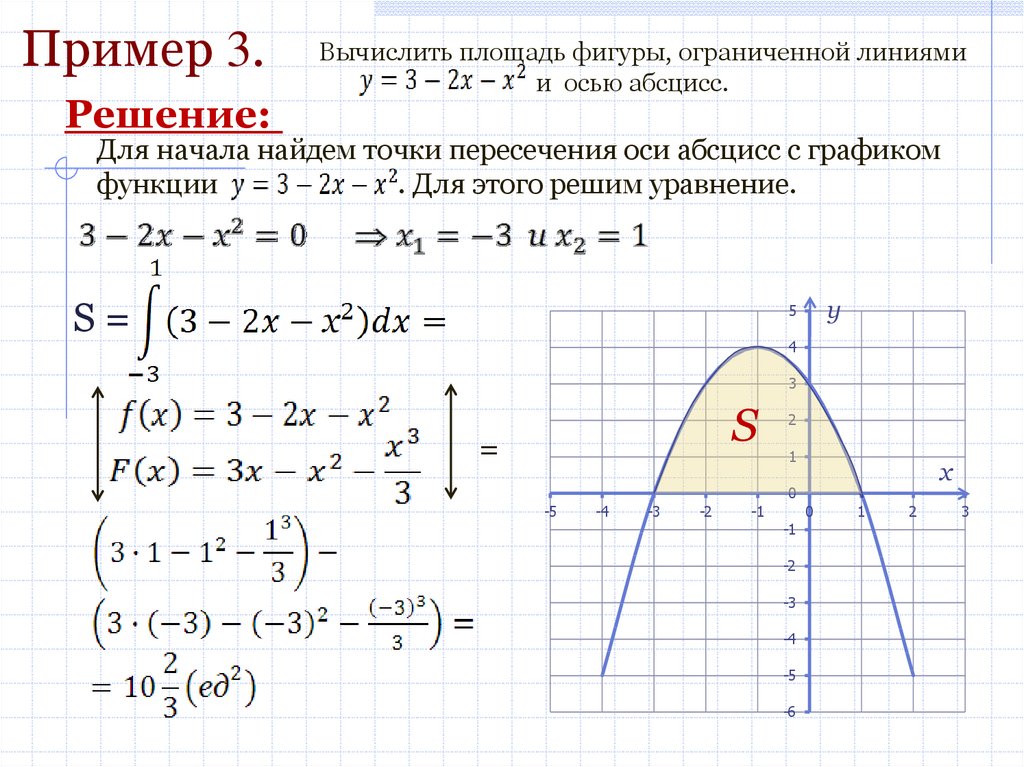
Пример 3.
Решение:
Вычислить площадь фигуры, ограниченной линиями
и осью абсцисс.
Для начала найдем точки пересечения оси абсцисс с графиком
функции
. Для этого решим уравнение.
S=
y
5
4
3
S
=
2
1
x
0
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
-5
-6
1
2
3

9.

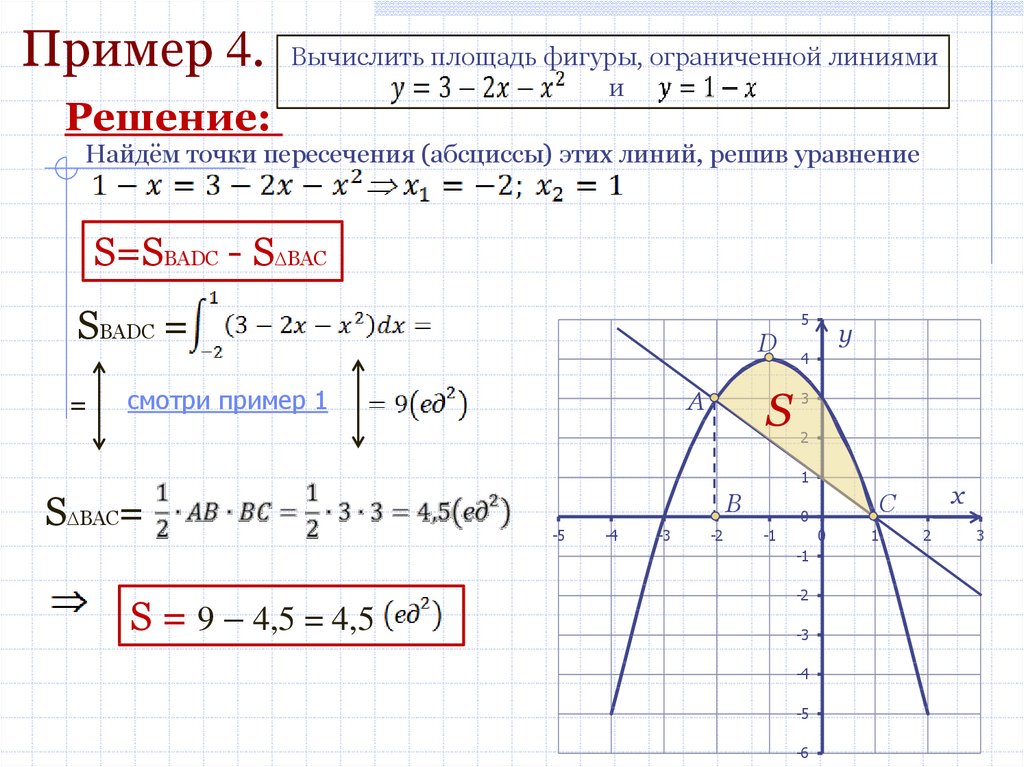
Пример 4.
Решение:
Вычислить площадь фигуры, ограниченной линиями
и
Найдём точки пересечения (абсциссы) этих линий, решив уравнение
S=SBADC - S BAC
SBADC =
=
5
D
смотри пример 1
S
A
y
4
3
2
1
S BAC=
B
-5
-4
-3
-2
-1
0
-1
S = 9 – 4,5 = 4,5
-2
-3
-4
-5
-6
x
C
0
1
2
3

10. Домашнее задание

На оценку «3» надо выполнить верно задания 1 уровня сложности.
Критерии оценки домашнего задания:
На оценку «4» надо выполнить верно задания 1, 2 уровней сложности
при двух- трех недочетах.
На оценку «5» надо выполнить верно все задания.
1 уровень сложности. Вычислите интегралы и выберите вариант ответа:
2
3
А) 3 2 x dx
Б)
1
2
2
В) Cosxdx
6dx
1
Г)
x
4
dx
1
6
2x
2
Д)
0
3
x 1 dx
x
3
Е)
2
2 x dx
0
2 уровень сложности. Вычислите площадь фигур, ограниченных линиями:
А)