Similar presentations:
Интеграл. Формула Ньютона - Лейбница
1.
•ИНТЕГРАЛ. ФОРМУЛАНЬЮТОНА-ЛЕЙБНИЦА
2.
Здравствуйте!1.Выполнить рисунок слайд №7
2.Внимательно изучите тему, слайд
6, 8
3.Записать,слайд №9
4. Записать, слайд №9,10,13
5. Рассмотрите пример нахождения
интеграла, слайд №17
3.
4.
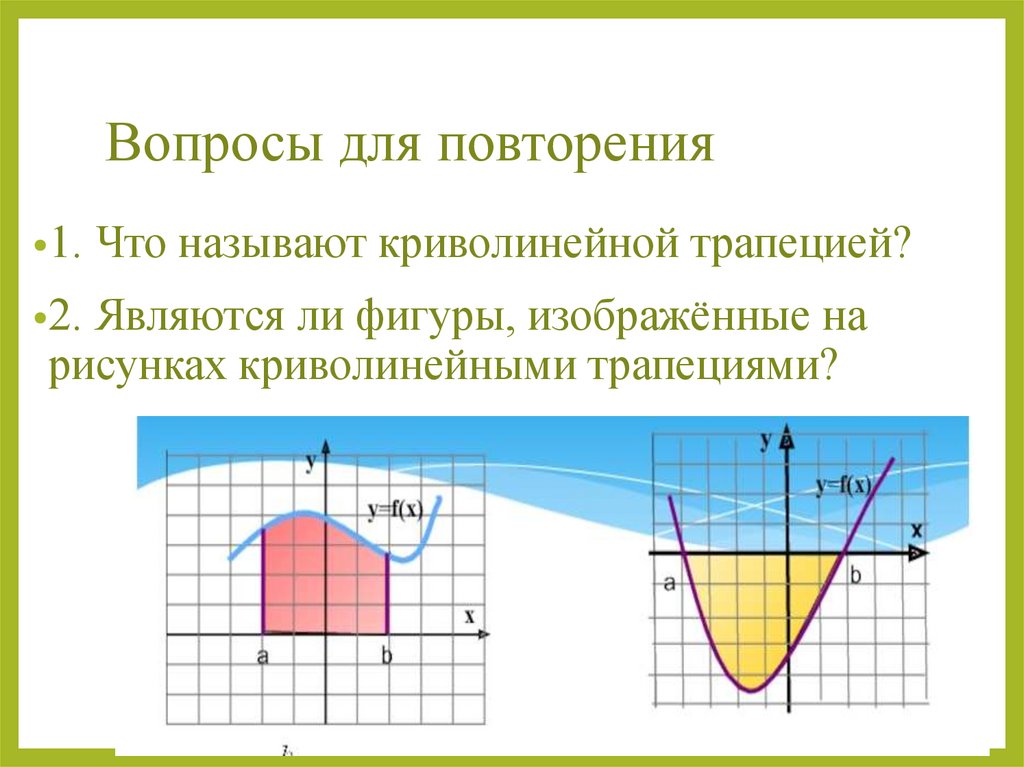
Вопросы для повторения•1. Что называют криволинейной трапецией?
•2. Являются ли фигуры, изображённые на
рисунках криволинейными трапециями?
5.
3. Запишите формулу длявычисления площади
криволинейной трапеции
6.
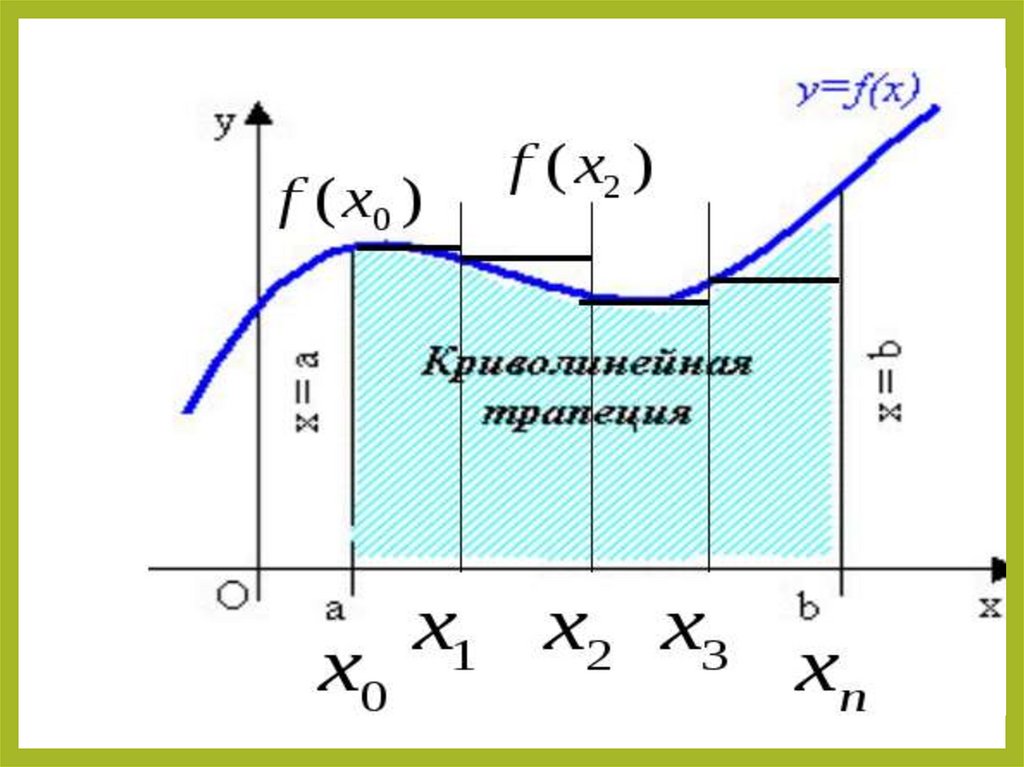
Рассмотрим другой подход к вычислениюплощади криволинейной трапеции
•Будем считать функцию f
неотрицательной и непрерывной на
отрезке [а; в], тогда площадь S
соответствующей криволинейной
трапеции можно приближённо
подсчитать следующим образом
7.
8.
Разобьём отрезок [а; в] на n отрезководинаковой длины точками
х 0 а х1 х 2 ... х n 1 х в
n
в а
х
n
Рассмотрим
сумму
S n f ( x 0 ) х f ( x1 ) х f ( x 2 ) х ... f ( x n 1 ) х
( f ( x 0 ) f ( x1 ) f ( x 2 ) ... f ( x n 1 )) х
9.
При n → ∞Sn→ к некоторому числу
Это число называют интегралом функции f
от а до в и обозначают:
в
∫ f(х)dх
а
10.
Числа а и в - называются пределамиинтегрирования, а – нижним пределом,
в – верхним.
Знак ∫ - называют знаком интеграла
Функцию f называют подынтегральной
функцией, а переменная х – переменной
интегрирования
dх- знак дифференциала
11.
Итак, если f( х ) ≥0 на отрезке [а; в], топлощадь соответствующей
криволинейной трапеции выражается
формулой:
в
S = ∫ f(х)dх
а
12.
•Сравнивая формулыкриволинейных трапеций :
в
S = ∫ f(х)dх и S = F(в) – F(а)
а
Делаем вывод:
13.
•Формула Ньютона-Лейбница14.
Иссак Ньютон(1643-1716)
Готфрид
Лейбниц(1646-1716).
15.
16.
17.
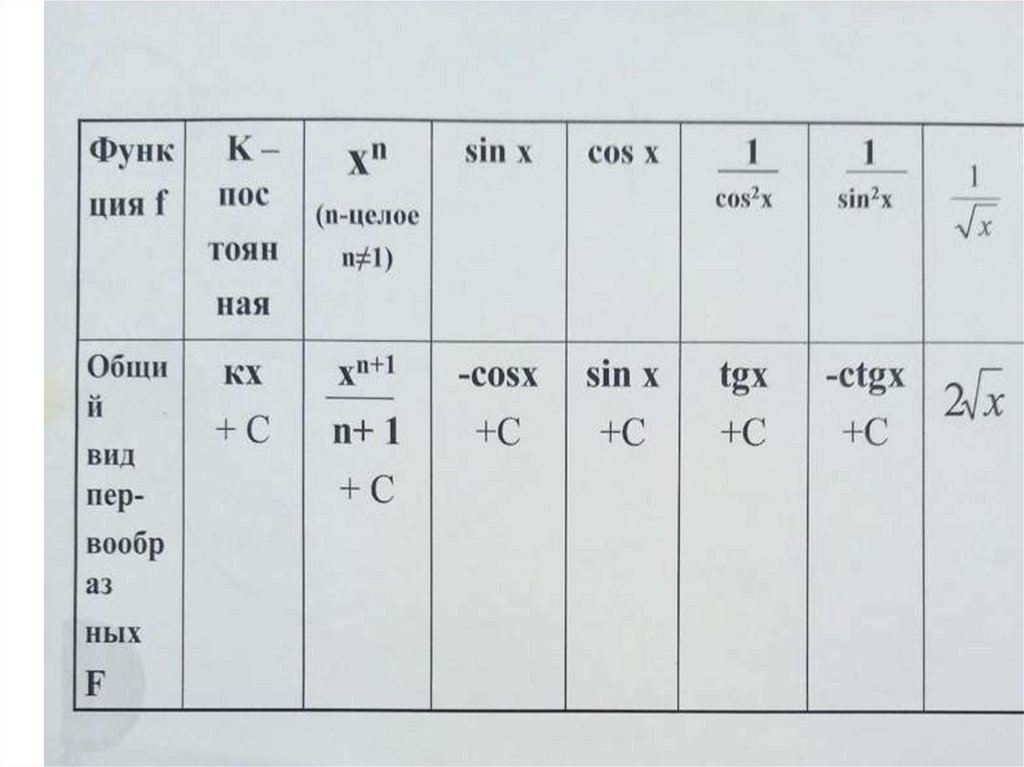
Пример:3
3
3
3
х
3
2
8
1
3
2
2 х dx 3 3 3 9 3 6 3
2
2
х2
2
2
2
(
2
х
4
)
dx
(
2
4
х
)
(
2
8
)
(
1
4 ) 12 5 7
1
2
1
18.
2х dx
2
0
2
х
3
dx
1
4
( 5 х 3 ) dx
1
3
0
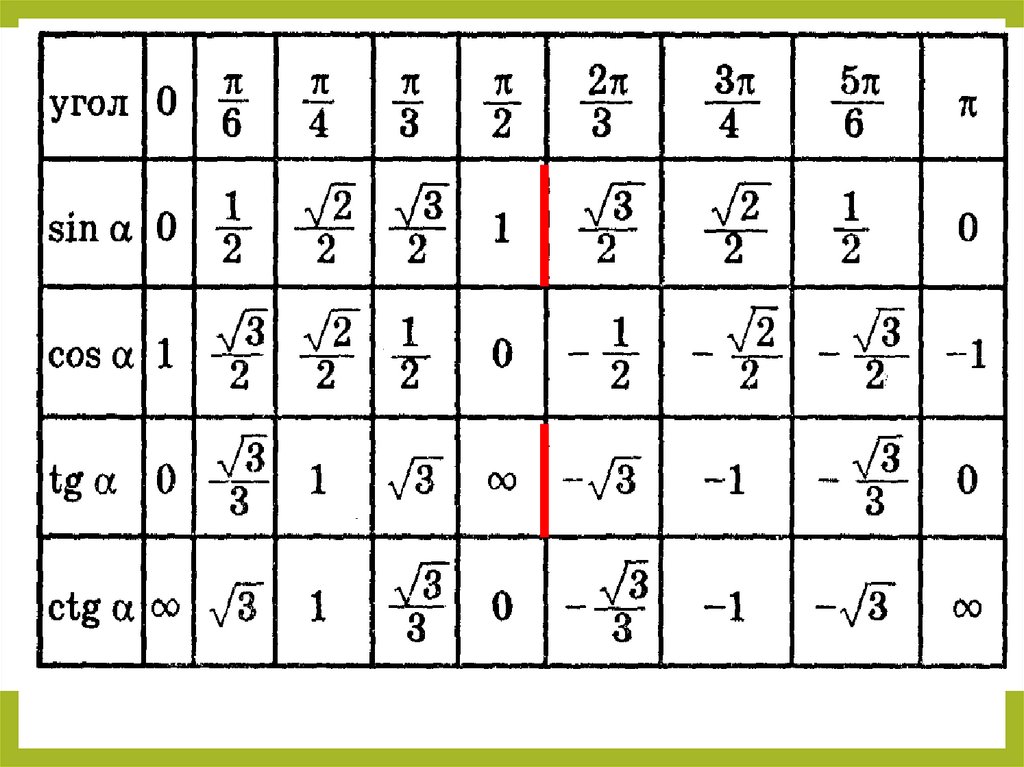
sin 5 x dx
П
2
dx
2
x













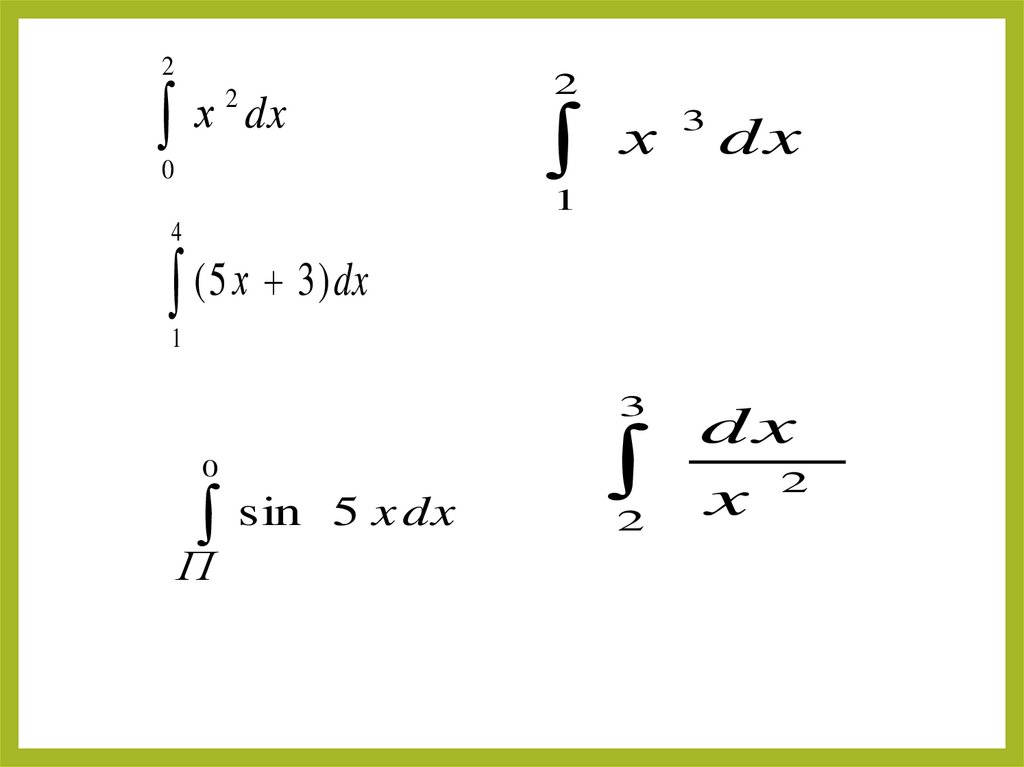
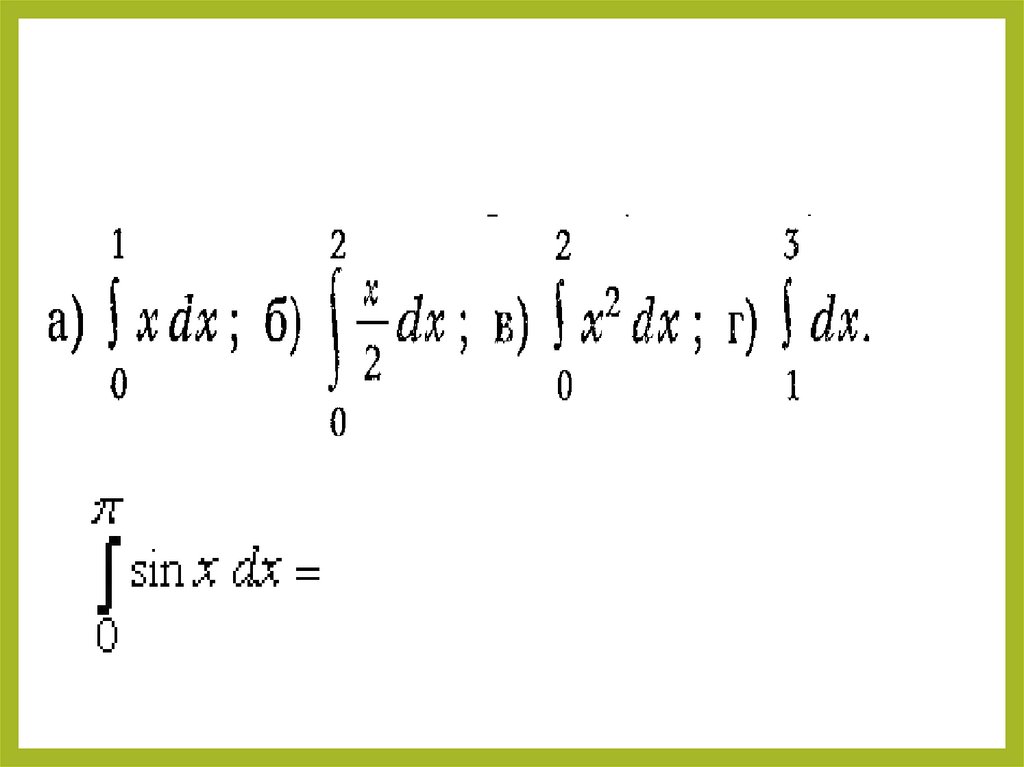
 mathematics
mathematics








