Componente şi circuite pasive - CCP

1. Componente şi circuite pasive - CCP

Cursul 3
Noţiuni introductive

2. Cuprins

Teoreme pentru analiza circuitelor electrice
Teoremele lui Kirchhoff
Principiul suprapunerii efectelor
Teorema lui Thevenin
Teorema lui Norton
2

3. Teoremele lui Kirchhoff http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Kirchhoff.html

Teoremele lui Kirchhof
http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Kir
chhof.html
Sunt aplicabile în descrierea funcţionării unui circuit dacă
acesta este considerat izolat (nu este expus acţiunii unor
factori exteni, de exemplu câmpuri electrice sau
magnetice).
Teorema lui Kirchhoff pentru tensiuni:
Suma algebrică a căderilor de tensiune de pe un ochi de
circuit este nulă.
Teorema lui Kirchhoff pentru curenţi:
Suma algebrică a curenţilor ce converg într-un nod de
circuit este nulă.
TKV : v 0 TKI : i 0
3

4. Aplicarea teoremelor lui Kirkhhoff

Aplicarea teoremelor lui
Se analizează circuitul din punct de vedere topologic: numărul de laturi
Kirkhhof
(notat cu l) şi numărul de noduri multiple (notat cu n). Descrierea
completă a funcţionării circuitului se obţine prin scrierea TKV pentru ln+1 ochiuri şi TKI pentru n-1 noduri multiple. Ochiurile alese trebuie să
formeze un sistem de ochiuri independente; acest sistem se formează
din ochiuri independente. Un ochi este independent faţă de un sistem
dat dacă conţine cel puţin o latură necomună cu acel sistem.
Dacă un circuit are m ochiuri şi n noduri, atunci descrierea completă a
funcţionării sale se obţine prin scrierea TKV pentru m-n+1 ochiuri şi TKI
pentru n-1 noduri multiple.
Pentru a scrie TKV pentru un ochi se alege un sens arbitrar de parcurgere
al ochiului (de exemplu sensul orar), tensiunile care au sensurile arbitrare
stabilite în acelaşi sens intră în suma algebrică cu semnul plus, iar cele cu
sensul arbitrar opus intră în suma algebrică cu semnul minus.
Pentru a scrie TKI pentru un nod curenţii care au sensul arbitrar intrând în
nod intră în suma algebrică cu semnul plus, iar curenţii care au sensul
arbitrar ieşind din nod intră în suma algebrică cu minus.
4

5. Aplicarea teoremelor lui Kirkhhoff

Aplicarea teoremelor lui
Kirkhhof
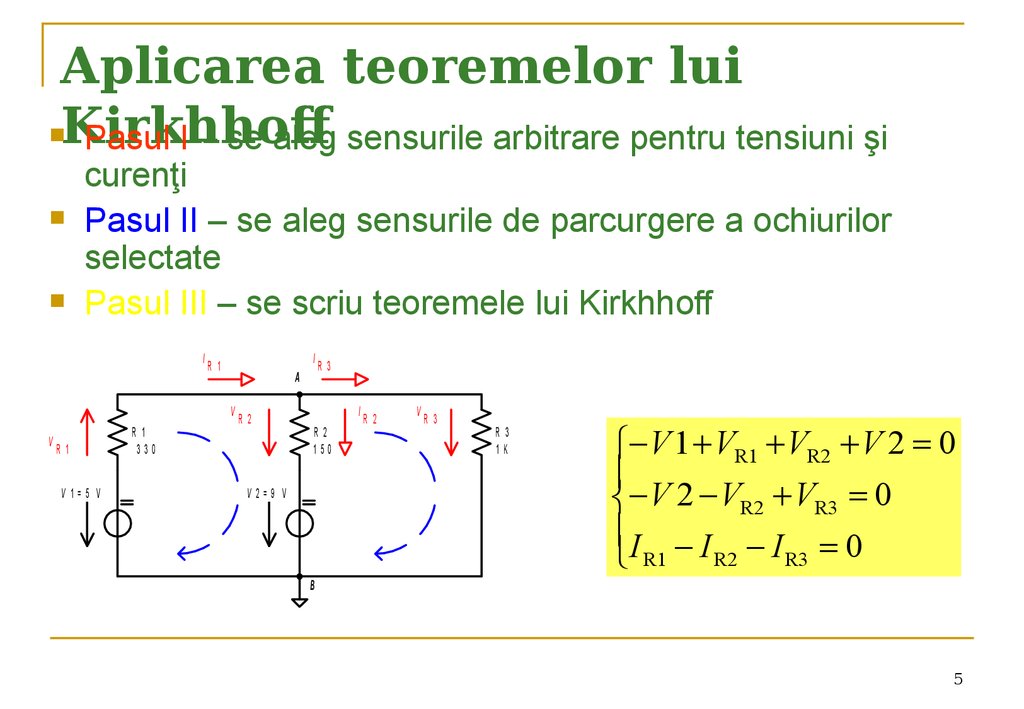
Pasul I – se aleg sensurile arbitrare pentru tensiuni şi
curenţi
Pasul II – se aleg sensurile de parcurgere a ochiurilor
selectate
Pasul III – se scriu teoremele lui Kirkhhoff
I
I
R1
A
V
V
R1
V1=5 V
R 1
330
R 2
R3
I
R2
150
V2=9 V
R 2
V
R 3
R 3
1K
V 1 VR1 VR2 V 2 0
V 2 VR2 VR3 0
I I I 0
R1 R2 R3
B
5

6. Rezolvarea sistemului de ecuaţii

Pentru rezolvarea sistemului se scriu
legile ce descriu relaţiile între
tensiunile şi curenţii elementelor de
circuit. (În exemplu, aplicăm legea lui
Ohm pentru rezistenţe şi substituim
în sistem tensiunile la bornele
rezistenţelor).
Se obţine un sistem de ecuaţii
algebrice deteminat (În exemplu un
sistem de trei ecuaţii cu trei
necunoscute, IR1, IR2 şi IR3).
VR1 R1 I R1
VR2 R 2 I R2
VR3 R3 I R3
R1 I R1 R 2 I R2 V 1 V 2
R 2 I R2 R3 I R3 V 2
I I I 0
R1 R2 R3
6

7. Soluţiile sistemului

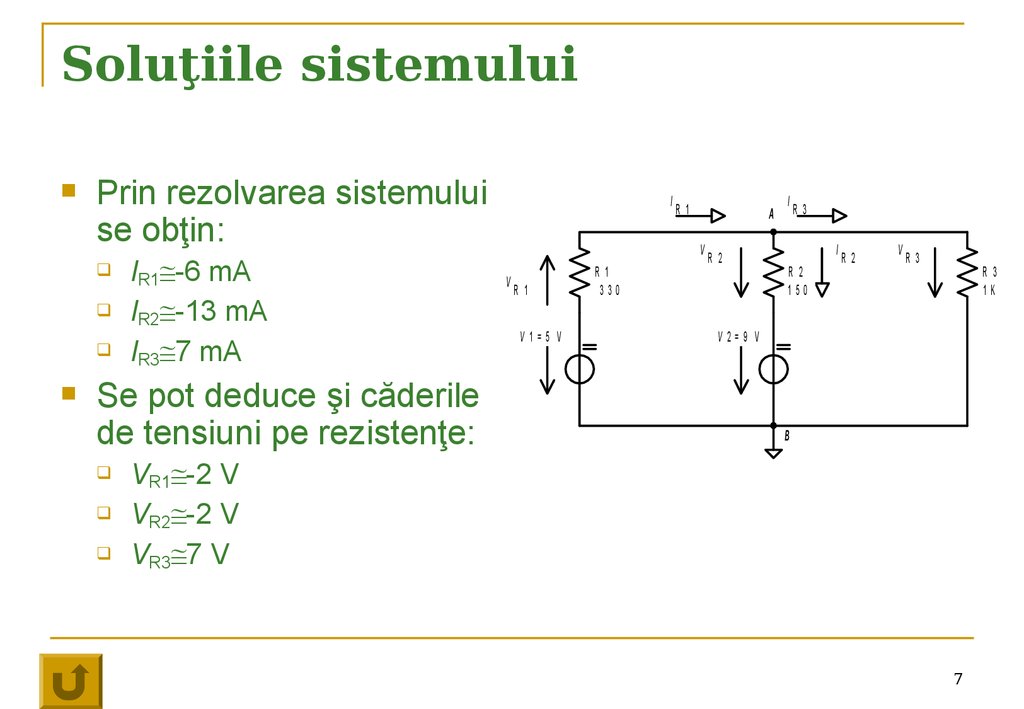
Prin rezolvarea sistemului
se obţin:
IR1 -6 mA
IR2 -13 mA
IR3 7 mA
Se pot deduce şi căderile
de tensiuni pe rezistenţe:
I
R1
A
V
V
R1
V1=5 V
R 1
330
R 2
I
R 3
I
R2
150
R2
V
R3
R 3
1K
V2=9 V
B
VR1 -2 V
VR2 -2 V
VR3 7 V
7

8. Circuite liniare şi circuite neliniare

Dacă transmitanţele definite pentru un circuit sunt mărimi
constante (grafic se reprezintă prin drepte în plane v-i, v-v
sau i-i) ele se numesc transmitanţe liniare.
Un circuit sau o componentă care are toate transmitanţele
liniare se numeşte circuit liniar sau componentă liniară.
Important: în general dispozitivele electronice şi circuitele
realizate cu ele sunt neliniare.
Procedeeul prin care funcţionarea unui circuit neliniar este
aproximată prin funcţionarea unui circuit liniar se numeşte
liniarizare.
8

9. Principiul suprapunerii efectelor

Pentru un circuit liniar este valabil principiul suprapunerii
efectelor:
Răspunsul circuitului la mai multe excitaţii simultane
(surse de semnal) se obţine determinând separat
răspunsurile parţiale ale acestuia la fiecare excitaţie iar
apoi răspunsul cumulat se obţine prin însumarea
acestora.
Pentru a obţine răspunsul circuitului la acţiunea unei
singe surse, celelalte surse din circuit trebuiesc
pasivizate.Prin pasivizare fiecare sursă ideală de
tensiune din circuit se înlocuieşte cu un scurtcircuit şi
fiecare sursă ideală de curent cu o întrerupere.
9

10. Teorema lui Thevènin

Comportarea unui circuit la o poartă poate fi înlocuită cu
compoartarea unei surse reale de tensiune având
teniunea egală cu tensiunea de mers în gol a porţii şi
rezistenţa de ieşire egală cu rezistenţa echivalentă
văzută la poarta respectivă pentru circuitul pasivizat.
Prin pasivizare fiecare sursă de tensiune din circuit se
înlocuieşte cu un scurtcircuit şi fiecare sursă de curent cu
o întrerupere.
10

11. Teorema lui Thevenin

Conform teoremei lui Thevenin circuitul haşurat poate fi echivalat la bornele AB cu o
sursă reală de tensiune. Trebuie să determinăm pentru această sursă tensiunea de
mers în gol, VO, şi rezistenţa de ieşire, RO.
I
A
V
R 1
330
V1=5 V
R 2
150
R 3
I
R 3
A
V
R 3
1K
R o
=?
R 3
R 3
R 3
1K
V2=9 V
V
C IR C U IT E L E C T R O N IC
B
O
=?
C IR C U IT
E C H IV A L E N T
B
11

12. Calcului tensiunii de mers în gol

Pentru a calcula
tensiunea de mers în gol
putem aplica teoremele
lui Kirchhoff.
Vom ilustra în continuare
aplicarea principiul
suprapunerii efectelor
pentru circuite liniare.
A
R1
330
R2
150
V
V1=5 V
V2=9 V
C IR C U IT E L E C T R O N IC
B
12
gol

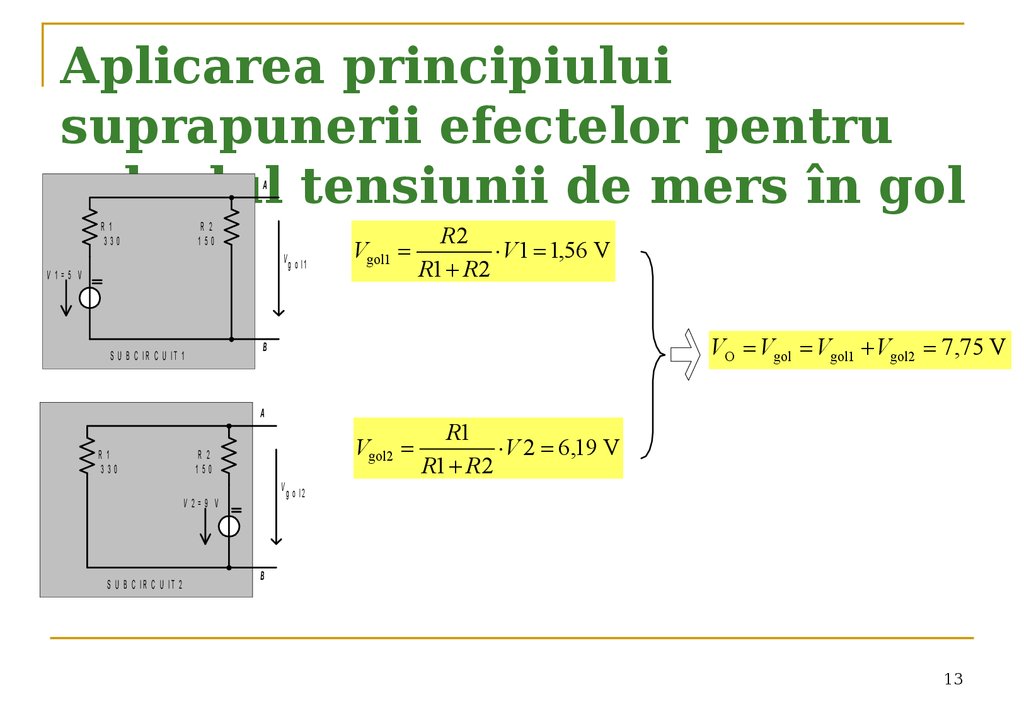
13. Aplicarea principiului suprapunerii efectelor pentru calculul tensiunii de mers în gol

A
R1
330
R2
150
V
V1=5 V
g o l1
Vgol1
VO Vgol Vgol1 Vgol2 7,75 V
B
S U B C IR C U IT 1
A
R1
330
Vgol2
R2
150
V
V2=9 V
S U B C IR C U IT 2
R2
V 1 1,56 V
R1 R 2
R1
V 2 6,19 V
R1 R 2
g o l2
B
13

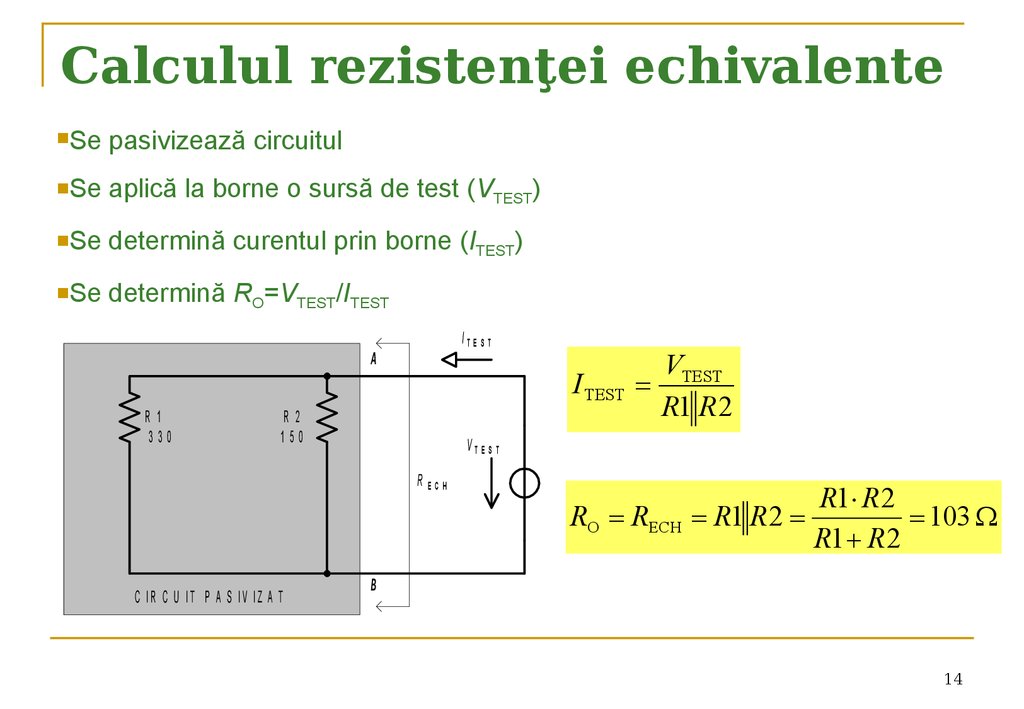
14. Calculul rezistenţei echivalente

Se
pasivizează circuitul
Se
aplică la borne o sursă de test (VTEST)
Se
determină curentul prin borne (ITEST)
Se
determină RO=VTEST/ITEST
ITE S T
A
R1
330
I TEST
R2
150
VTEST
R1 R 2
VTE ST
R
EC H
RO RECH
C IR C U IT P A S IV IZ A T
R1 R 2
R1 R 2
103
R1 R 2
B
14

15. Concluzie

I
A
V
R o
=103
V
O
= 7 ,7 5 V
C IR C U IT
E C H IV A L E N T
R3
R 3
R3
1K
Din punctul de vedere al
rezistenţei R3 circuitul
echivalent va avea
acelaşi efect:
I R3
VO
7,75 V
7 mA
RO R3 1103
VR3 R3 I R3 7 mA 1 KΩ 7 V
B
15

16. Teorema lui Norton

Comportarea unui circuit la o poartă poate fi înlocuită cu
compoartarea unei surse reale de curent având curentul
egal cu curentul de mers în scurtcircuit al porţii şi
rezistenţa de ieşire egală cu rezistenţa echivalentă
văzută la poarta respectivă pentru circuitul pasivizat.
Prin pasivizare fiecare sursă de tensiune din circuit se
înlocuieşte cu un scurtcircuit şi fiecare sursă de curent cu
o întrerupere.
16

17. Teorema lui Norton

Conform teoremei lui Norton circuitul haşurat poate fi echivalat la bornele AB cu o
sursă reală de curent. Trebuie să determinăm pentru această sursă curentul de mers
în scurtcircuit, ISC, şi rezistenţa de ieşire, RO.
I
A
R 2
150
R3
R3
1K
R o
R 3
1K
=?
V
V1=5 V
R 3
A
V
R1
330
I
R 3
R 3
V2=9 V
I
C IR C U IT E L E C T R O N IC
B
O
=?
C IR C U IT
E C H IV A L E N T
B
17

18. Calcului curentului de mers în scurtcircuit

Pentru a calcula curentul
de scurtcircuit putem
aplica teoremele lui
Kirchhoff.
Ilustrăm din nou aplicarea
principiului suprapunerii
efectelor pentru circuite
liniare.
A
R1
330
V1=5 V
R2
150
Isc
V2=9 V
C IR C U IT E L E C T R O N IC
B
18

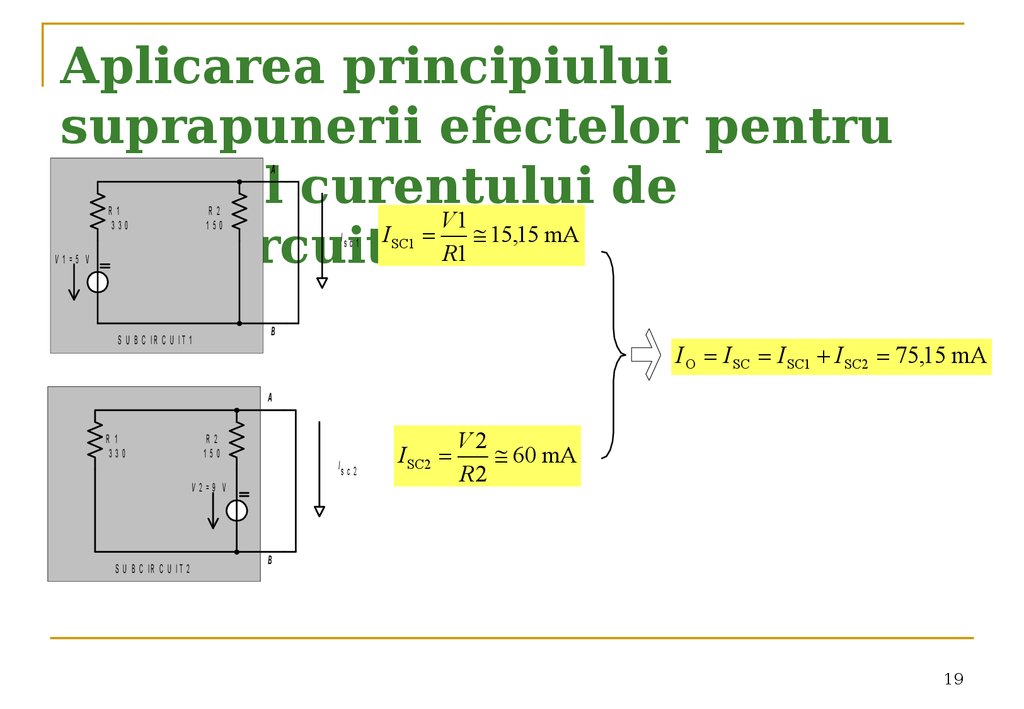
19. Aplicarea principiului suprapunerii efectelor pentru calculul curentului de scurtcircuit

Aplicarea principiului
suprapunerii efectelor pentru
calculul curentului
de
V1
I
15,15 mA
R
1
scurtcircuit
A
R1
330
R2
150
Is c 1
SC1
V1=5 V
B
S U B C IR C U IT 1
I O I SC I SC1 I SC2 75,15 mA
A
R1
330
R2
150
Is c 2
V2=9 V
S U B C IR C U IT 2
I SC2
V2
60 mA
R2
B
19

20. Calculul rezistenţei echivalente

ITE S T
A
R1
330
R2
150
VTE S T
RECH
C IR C U IT P A S IV IZ A T
RO RECH
R1 R 2
R1 R 2
103
R1 R 2
B
20

21. Concluzie

I
R 3
A
R o
R 3
1K
=103
V
I
O
= 7 5 ,1 5 m A
C IR C U IT
E C H IV A L E N T
R 3
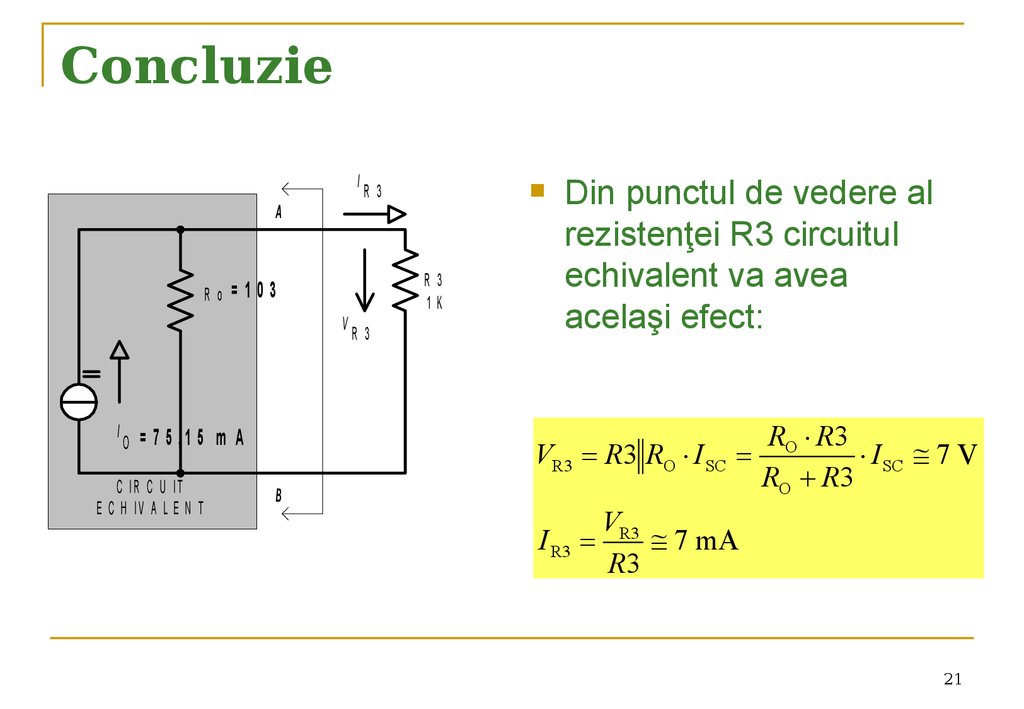
Din punctul de vedere al
rezistenţei R3 circuitul
echivalent va avea
acelaşi efect:
VR3 R3 RO I SC
B
I R3
RO R3
I SC 7 V
RO R3
VR3
7 mA
R3
21

22. Trecerea de la echivalenţa Thevenin la echivalenţa Norton

Odată determinat unul dintre circuitele echivalente (Thevenin
sau Norton), celălalt se obţine direct aplicând relaţia:
I ONorton
VOThevenin
RO
În cazul exemplului prezentat se obţine direct:
I ONorton
VOThevenin 7,75 V
75,15 mA
RO
103
22

23. Recomandări pentru studiul individual

Pentru circuitul următor să se determine curentul prin
rezistenţa R şi tensiunea la bornele ei aplicând:
Teoremele lui Kirchhoff
Echivalenţa Thevenin şi/sau Norton
(utilizaţi principiul suprapunerii efectelor)
R 3
V2
R 4
2k
7k
9V
R
I2
1k
R 1
R 2
2k
4k
1m Adc
23