Componente şi circuite electronive pasive – CCEP Elemente de circuit – capacitatea

1. Componente şi circuite electronive pasive – CCEP Elemente de circuit – capacitatea (II)

CURSUL 6
Componente şi circuite electronive pasive –
CCEP
Elemente de circuit – capacitatea (II)
1

2. Cuprins

Comportare în regim tranzitoriu
◦ Încărcarea unei capacităţi de la o sursă de tensiune constantă
◦ Descărcarea capacităţii pe o rezistenţă
◦ Circuit RC serie comandat cu impulsuri de tensiune
◦ Încărcarea unei capacităţi de la o sursă de curent constant
◦ Circuit RC serie comandat cu impulsuri de curent
2

3. Comportarea capacităţii în regim tranzitoriu

Regimul tranzitoriu în acest caz reprezintă modificarea stării de curent
continuu din circuit cu o nouă stare de curent continuu.
Pe durata acestor modificări capacităţile nu pot fi considerate nici
întreruperi nici scurtcircuite.
Analiza de regim tranzitoriu presupune determinarea modului în care
se încarcă şi se descarcă capacităţile.
Funcţionarea circuitelor în acest tip de regim este descrisă de ecuaţii
diferenţiale.
3

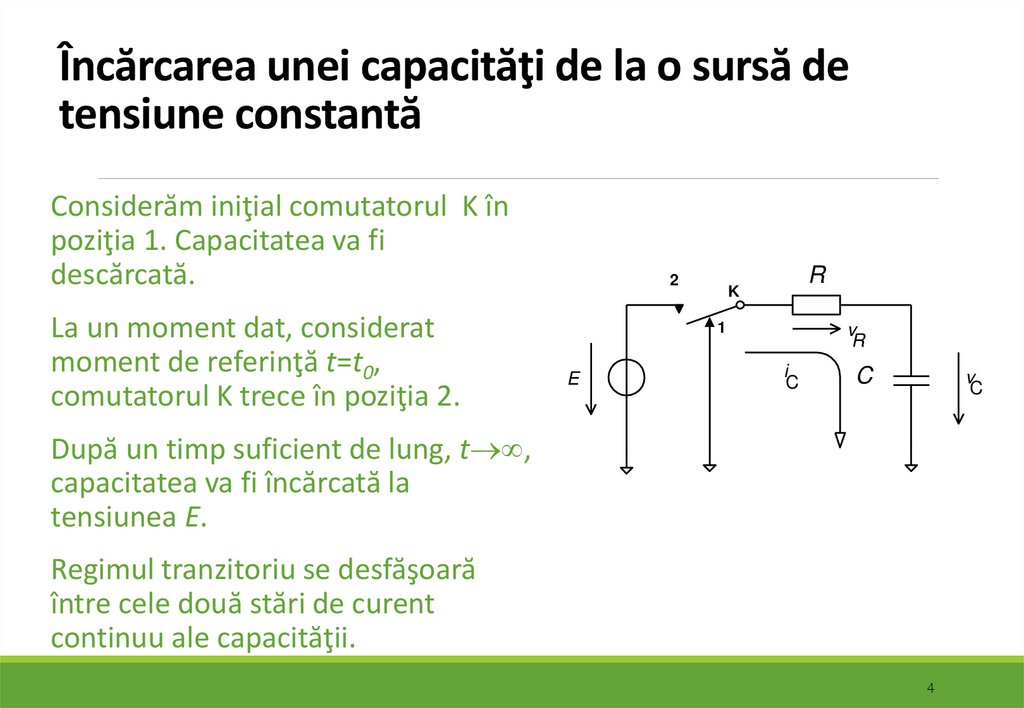
4. Încărcarea unei capacităţi de la o sursă de tensiune constantă

Considerăm iniţial comutatorul K în
poziţia 1. Capacitatea va fi
descărcată.
La un moment dat, considerat
moment de referinţă t=t0,
comutatorul K trece în poziţia 2.
2
R
K
1
E
v
R
i
C
C
v
C
După un timp suficient de lung, t ,
capacitatea va fi încărcată la
tensiunea E.
Regimul tranzitoriu se desfăşoară
între cele două stări de curent
continuu ale capacităţii.
4

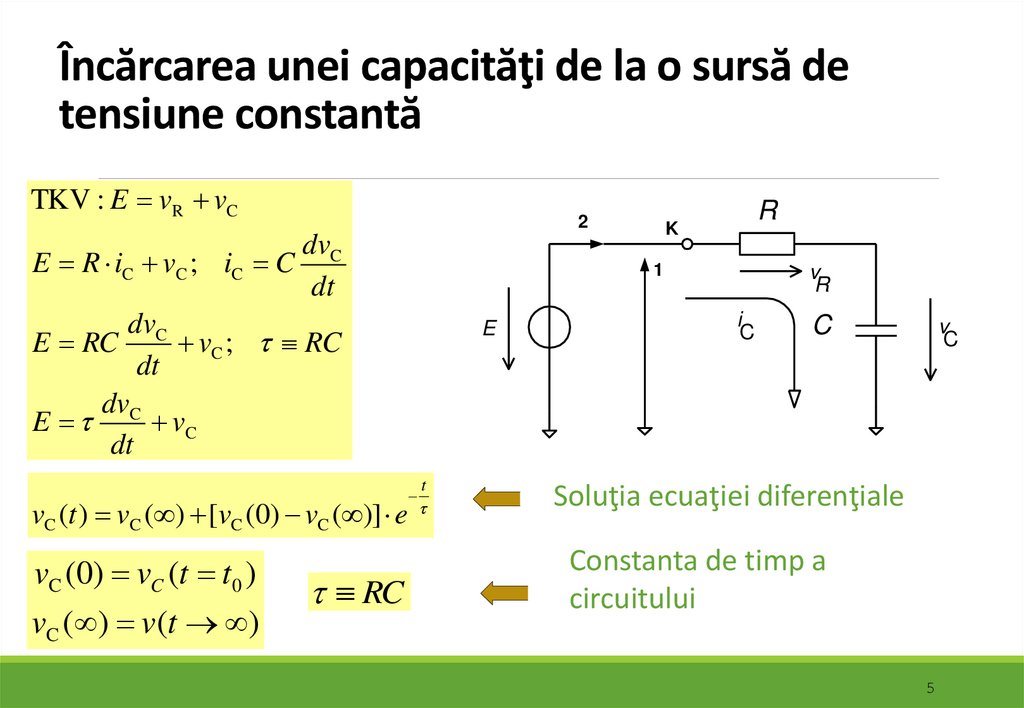
5. Încărcarea unei capacităţi de la o sursă de tensiune constantă

TKV : E vR vC
E R iC vC ; iC C
2
dvC
dt
1
dvC
E RC
vC ; RC
dt
dvC
E
vC
dt
vC (t ) vC ( ) [vC (0) vC ( )] e
vC (0) vC (t t0 )
vC ( ) v(t )
RC
R
K
E
t
v
R
i
C
C
v
C
Soluţia ecuaţiei diferenţiale
Constanta de timp a
circuitului
5

6. Variaţia tensiunii pe capacitate, vC

vC (0) 0; vC ( ) E
t
vC (t ) E (1 e )
vR (t ) E vC (t ) E e
t
6

7. Variaţia curentului prin capacitate, iC

E vC (t ) E
iC (t )
e
R
R
t
7

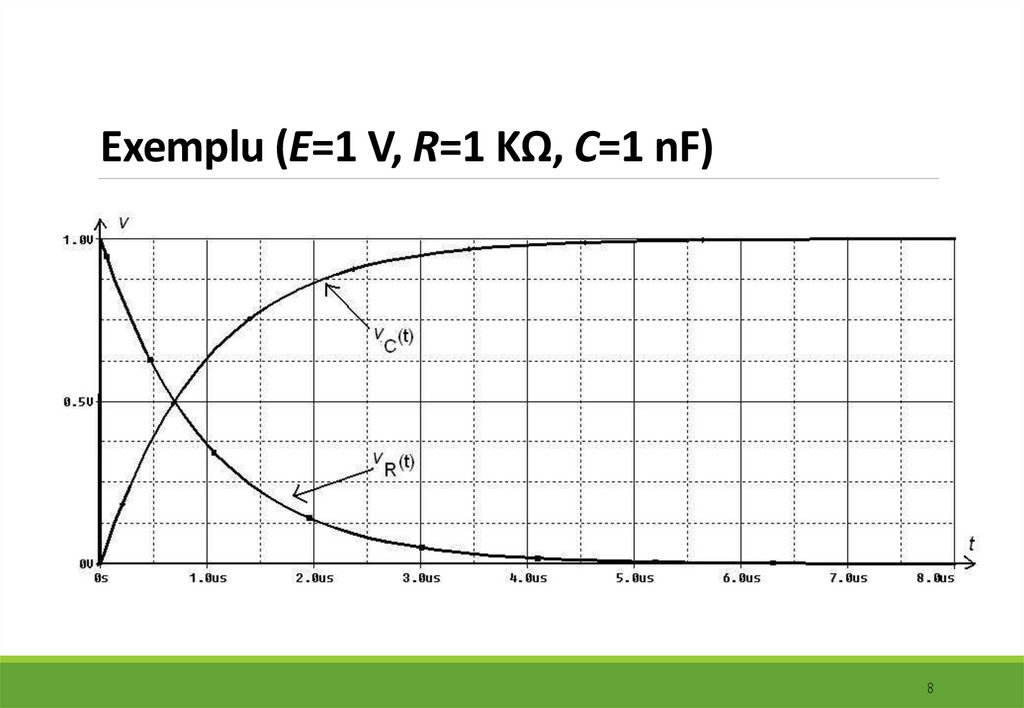
8. Exemplu (E=1 V, R=1 KΩ, C=1 nF)

8

9. Descărcarea capacităţii pe o rezistenţă

Considerăm iniţial comutatorul K în
poziţia 2. Capacitatea va fi încărcată
la tensiunea E.
La un moment dat, considerat
moment de referinţă t=t0,
comutatorul K trece în poziţia 1.
2
R
K
1
E
v
R
i
C
C
v
C
După un timp suficient de lung,
t , capacitatea va fi complect
descărcată.
Regimul tranzitoriu se desfăşoară
între cele două stări de curent
continuu ale capacităţii.
9

10. Descărcarea capacităţii pe o rezistenţă

TKV : 0 vR vC
0 R iC vC ; iC C
2
dvC
dt
1
vC (0) vC (t t0 ) E
vC ( ) v(t ) 0
v
R
i
C
E
dv
0 RC C vC ; RC
dt
dv
0 C vC
dt
vC (t ) vC ( ) [vC (0) vC ( )] e
R
K
t
C
v
C
Soluţia ecuaţiei diferenţiale
t
vC (t ) E e ; vR (t ) vC (t )
t
vR (t )
E
iC (t )
e
R
R
10

11. Exemplu (E=1 V, R=1 KΩ, C=1 nF)

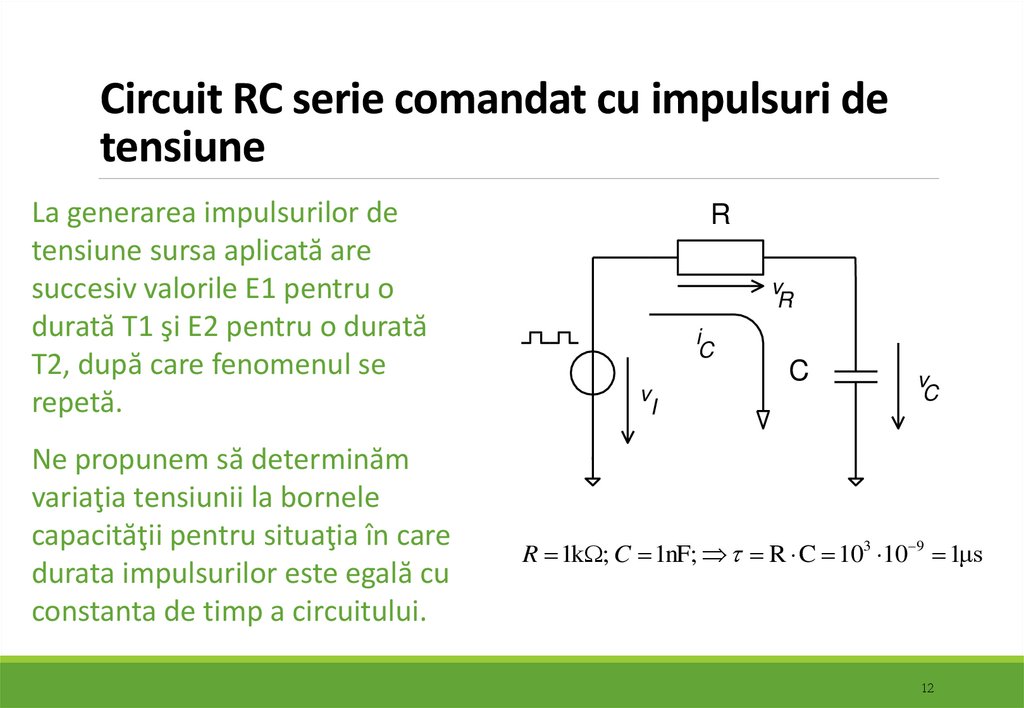
11

12. Circuit RC serie comandat cu impulsuri de tensiune

La generarea impulsurilor de
tensiune sursa aplicată are
succesiv valorile E1 pentru o
durată T1 şi E2 pentru o durată
T2, după care fenomenul se
repetă.
Ne propunem să determinăm
variaţia tensiunii la bornele
capacităţii pentru situaţia în care
durata impulsurilor este egală cu
constanta de timp a circuitului.
R
v
R
i
C
v
I
C
v
C
R 1k ; C 1nF; R C 103 10 9 1μs
12

13. Circuit RC serie comandat cu impulsuri de tensiune

Pe intervalul de timp [0; 1 s]:
Facem analiza pentru:
o durată a impulsurilor
T1=T2=1 s
E1=1V; E2=0V
vC (0) 0; vC ( ) E1 1V
t
vC (t ) E1 (1 e ) 1V (1 e
t
1μs
)
La terminarea intervalului de timp
Impulsurile încep prin aplicarea tensiunea pe capacitate va fi:
valorii E1
1μs
Tensiunea iniţială pe capacitate vC (1μs) 1V (1 e
1μs
) 0,63V
vC(0)=0V.
13

14. Circuit RC serie comandat cu impulsuri de tensiune

Pe intervalul de timp [1 s; 2 s]:
vC (0) 0,63V; vC ( ) E 2 0V
vC (t ) vC (0) e
t
0,63V e
t
1μs
La terminarea intervalului de timp
tensiunea pe capacitate va fi:
vC (1μs) 0,63V e
1μs
1μs
0,63V 0,37 0,23V
Pe intervalul de timp [2 s; 3 s]:
vC (0) 0,23V; vC ( ) E1 1V
vC (t ) 1V (0,23V 1V) e
1V 0,77V e
t
1μs
t
1μs
La terminarea intervalului de timp
tensiunea pe capacitate va fi:
vC (1μs) 1V 0,77V e
1μs
1μs
0,72V
14

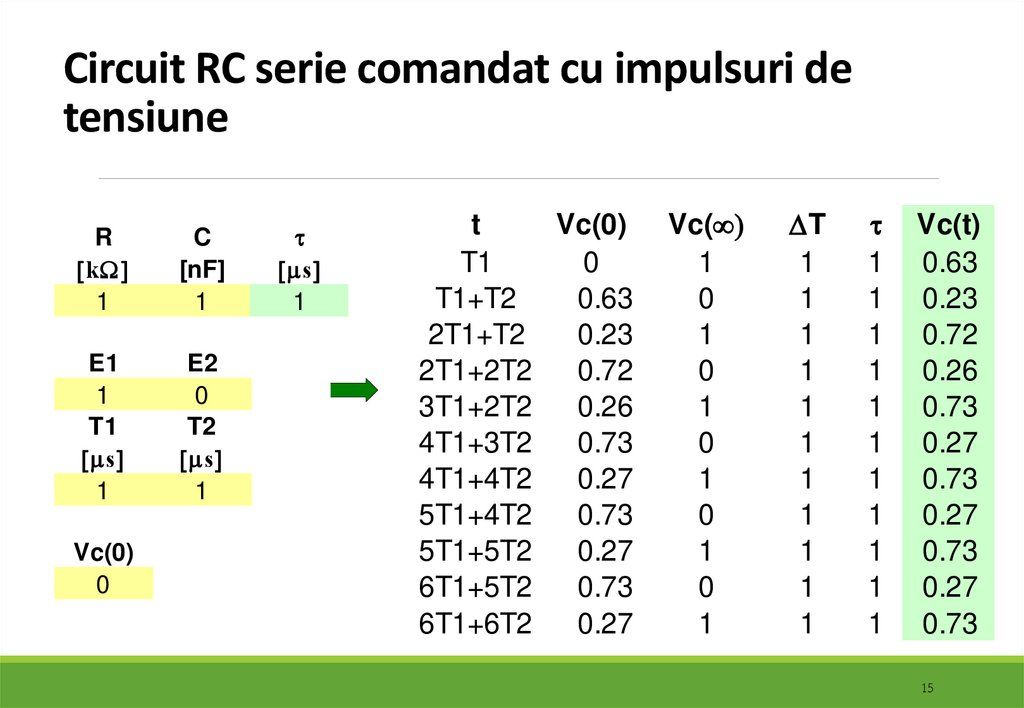
15. Circuit RC serie comandat cu impulsuri de tensiune

R
k
1
C
[nF]
1
E1
1
T1
s
1
E2
0
T2
s
1
Vc(0)
0
s
1
t
Vc(0)
T1
0
T1+T2
0.63
2T1+T2
0.23
2T1+2T2
0.72
3T1+2T2
0.26
4T1+3T2
0.73
4T1+4T2
0.27
5T1+4T2
0.73
5T1+5T2
0.27
6T1+5T2
0.73
6T1+6T2
0.27
Vc(
1
0
1
0
1
0
1
0
1
0
1
T
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Vc(t)
0.63
0.23
0.72
0.26
0.73
0.27
0.73
0.27
0.73
0.27
0.73
15

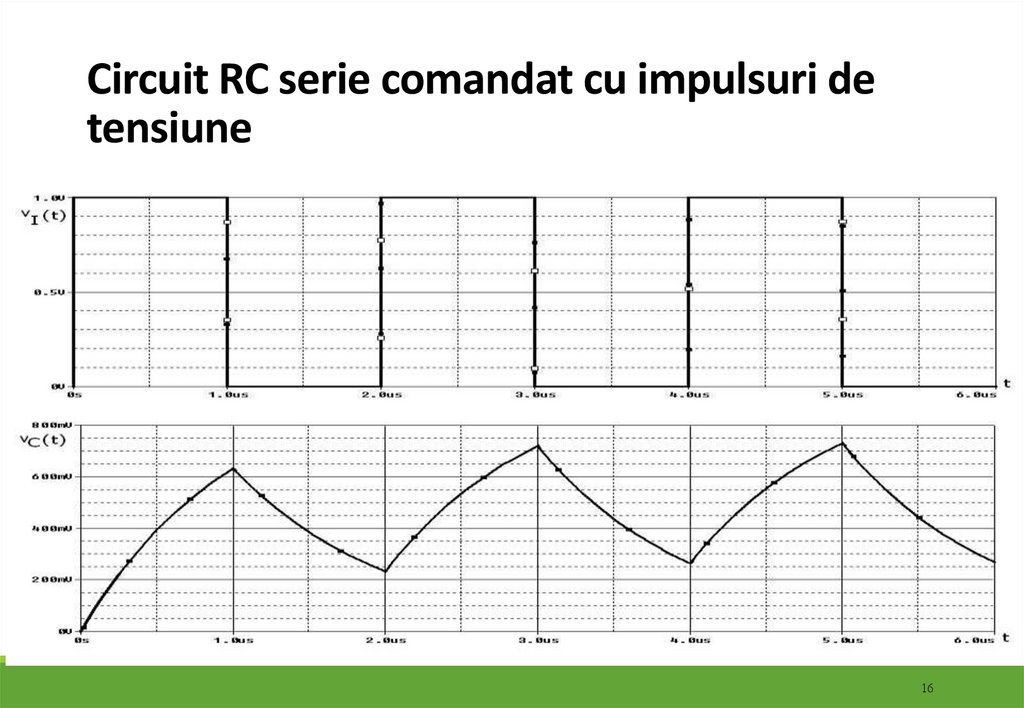
16. Circuit RC serie comandat cu impulsuri de tensiune

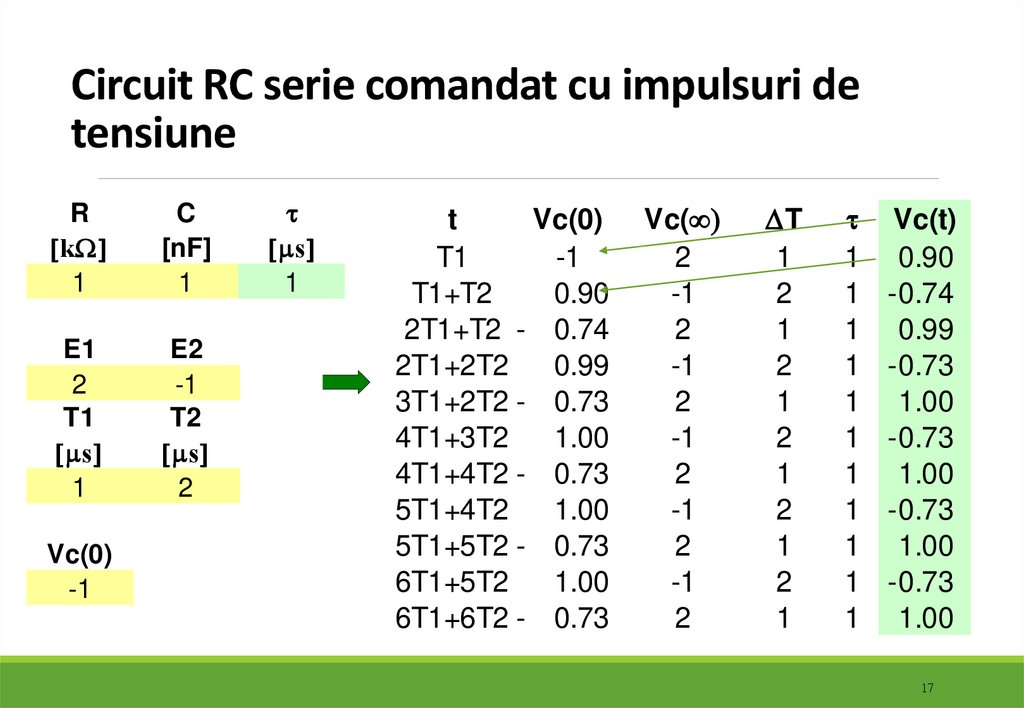
16

17. Circuit RC serie comandat cu impulsuri de tensiune

R
k
1
C
[nF]
1
E1
2
T1
s
1
E2
-1
T2
s
2
Vc(0)
-1
s
1
t
Vc(0)
T1
-1
T1+T2
0.90
2T1+T2 - 0.74
2T1+2T2
0.99
3T1+2T2 - 0.73
4T1+3T2
1.00
4T1+4T2 - 0.73
5T1+4T2
1.00
5T1+5T2 - 0.73
6T1+5T2
1.00
6T1+6T2 - 0.73
Vc(
2
-1
2
-1
2
-1
2
-1
2
-1
2
T
1
2
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
1
1
1
1
Vc(t)
0.90
- 0.74
0.99
- 0.73
1.00
- 0.73
1.00
- 0.73
1.00
- 0.73
1.00
17

18. Circuit RC serie comandat cu impulsuri de tensiune

18

19. Comportarea circuitelor RC la aplicarea unui tren de impulsuri

Reluăm circuitul RC serie căruia sursa
de semnal vI îi aplică un tren de
impulsuri dreptunghiulare.
În analiza următoare vom lua în
considerare atât tensiunea de la
bornele capacităţii, vC(t), cât şi
tensiunea de la bornele rezistenţei,
vR(t).
R
v
R
i
C
v
I
C
v
C
Prin aplicarea sursei de semnal se
repetă succesiv fenomenele de
încărcarea şi descărcare a capacităţii
prezentate la descrierea regimurilor
tranzitorii anterioare.
19

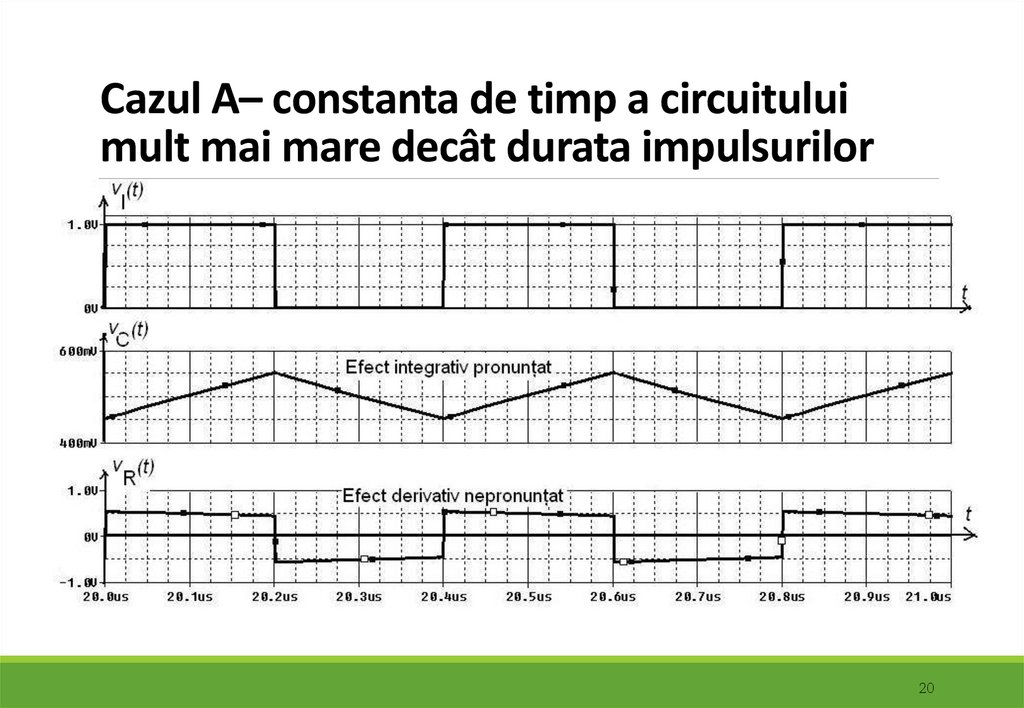
20. Cazul A– constanta de timp a circuitului mult mai mare decât durata impulsurilor

20

21. Circuit integrator

Dacă tensiunea de ieşire este tensiunea de pe capacitate efectul
circuitului asupra semnalului de intrare este de atenuare a fronturilor,
fiind similar cu cel al operaţiei matematice de integrare.
În această situaţie, vO(t)=vC(t), circuitul se numeşte circuit de integrare.
Efectul de integrare este mai pronunţat în cazul în care constanta de
timp a circuitului este mai mare decât durata impulsurilor.
Funcţia de integrare realizată în regim tranzitoriu este corespondentă
funcţiei de FTJ realizată în CA.
21

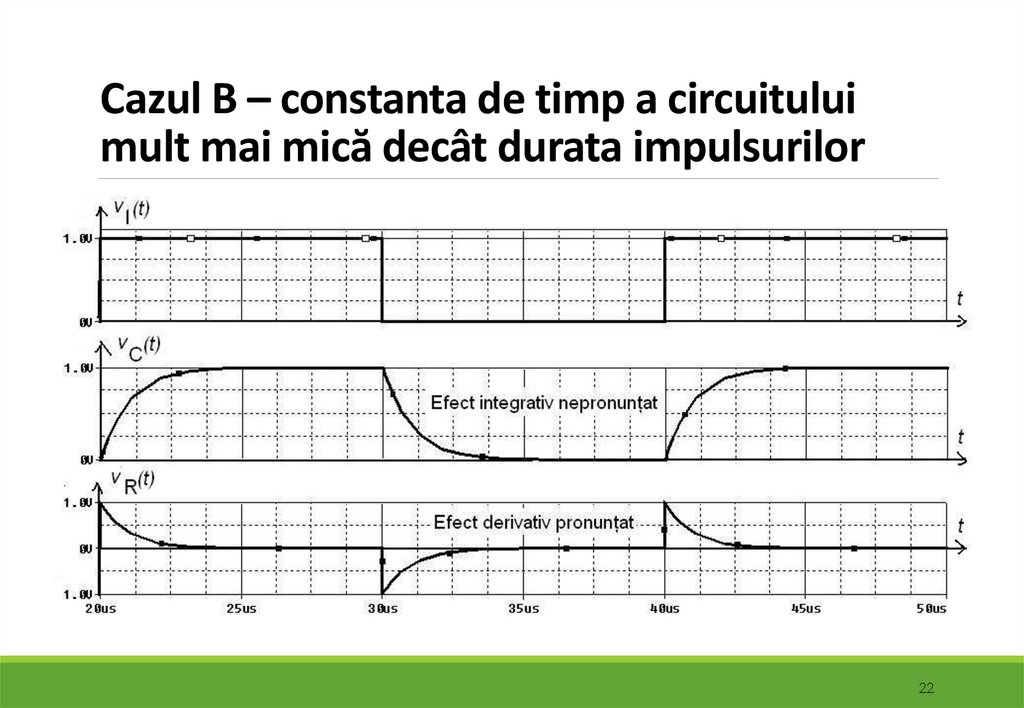
22. Cazul B – constanta de timp a circuitului mult mai mică decât durata impulsurilor

22

23. Circuit derivator

Dacă tensiunea de ieşire este tensiunea de pe rezistenţă efectul
circuitului asupra semnalului de intrare este de accentuare a
fronturilor, fiind similar cu cel al operaţiei matematice de derivare.
În această situaţie, vO(t)=vR(t), circuitul se numeşte circuit de derivare.
Efectul de derivare este mai pronunţat în cazul A, în care constanta de
timp a circuitului este mai mică decât durata impulsurilor.
Funcţia de derivare realizată în regim tranzitoriu este corespondentă
funcţiei de FTS realizată în CA.
23

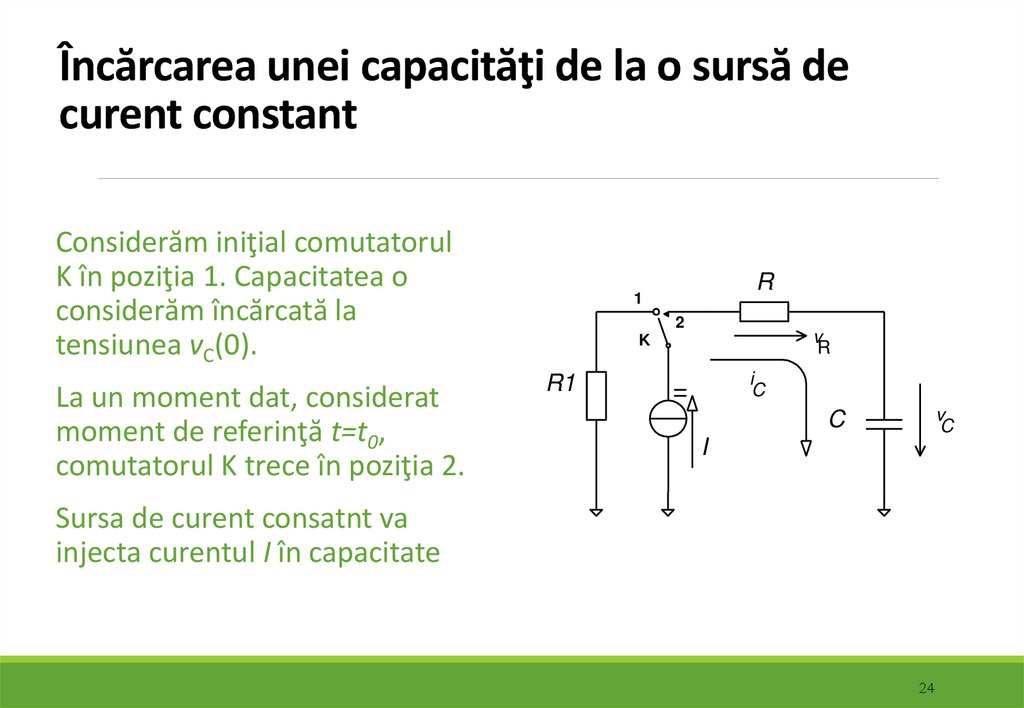
24. Încărcarea unei capacităţi de la o sursă de curent constant

Considerăm iniţial comutatorul
K în poziţia 1. Capacitatea o
considerăm încărcată la
tensiunea vC(0).
La un moment dat, considerat
moment de referinţă t=t0,
comutatorul K trece în poziţia 2.
R
1
2
v
R
K
i
C
R1
v
C
C
I
Sursa de curent consatnt va
injecta curentul I în capacitate
24

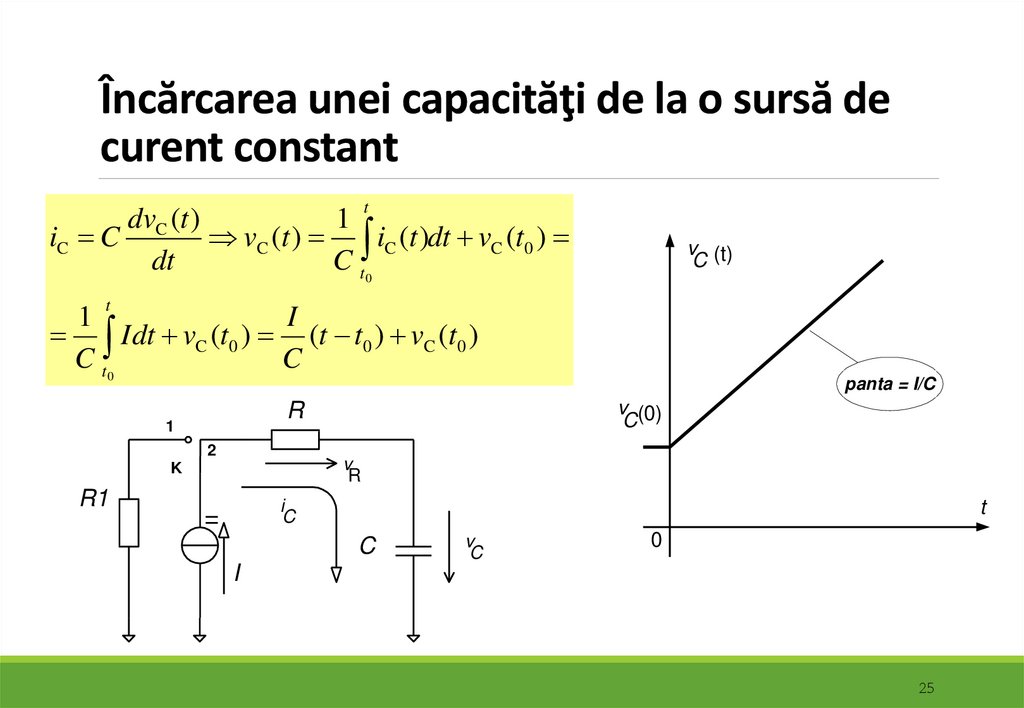
25. Încărcarea unei capacităţi de la o sursă de curent constant

t
dvC (t )
1
iC C
vC (t ) iC (t )dt vC (t0 )
dt
C t0
v (t)
C
t
1
I
I dt vC (t0 ) (t t0 ) vC (t0 )
C t0
C
v (0)
C
R
1
2
panta = I/C
v
R
K
R1
i
C
t
C
v
C
0
I
25

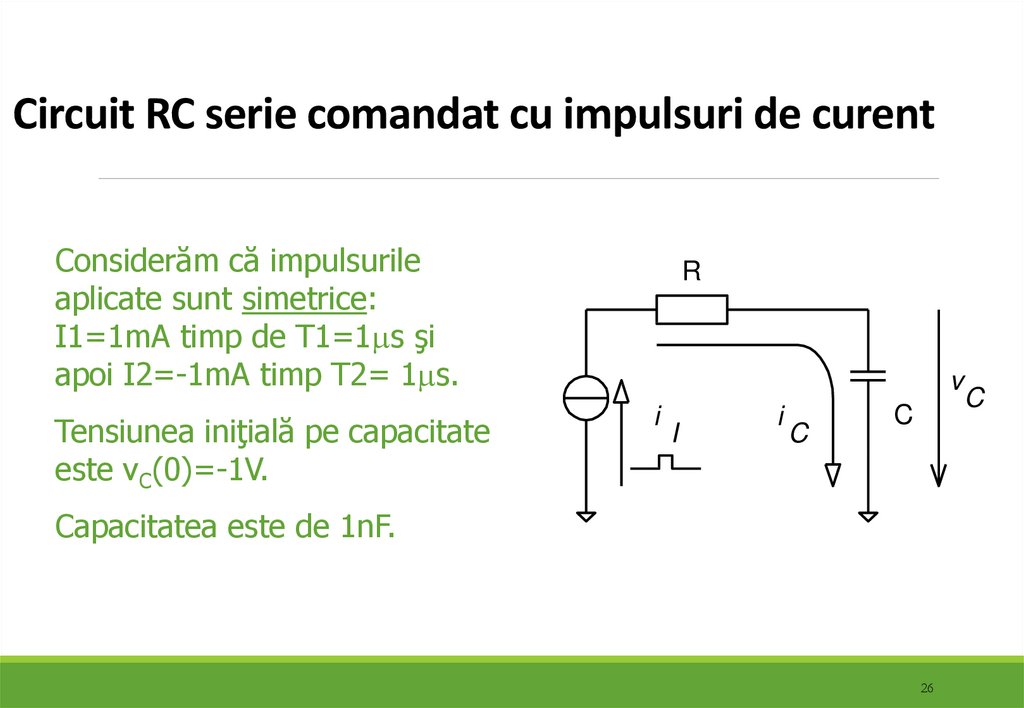
26. Circuit RC serie comandat cu impulsuri de curent

Considerăm că impulsurile
aplicate sunt simetrice:
I1=1mA timp de T1=1 s şi
apoi I2=-1mA timp T2= 1 s.
Tensiunea iniţială pe capacitate
este vC(0)=-1V.
R
v
i
I
i
C
C
Capacitatea este de 1nF.
26
C

27. Circuit RC serie comandat cu impulsuri de curent

Pe intervalul de timp [0 s; 1 s] panta
tensiunii la bornele capacităţii va fi:
R
V
I1 1mA
V
1
vC (t ) v C (0) 1 t
C 1nF
μs
μs
v
i
La sfârşitul intervalului de timp
tensiunea la bornele capacităţii va fi:
I
i
C
C
V
vC (1μs) 1V 1 1μs 0V
μs
27
C

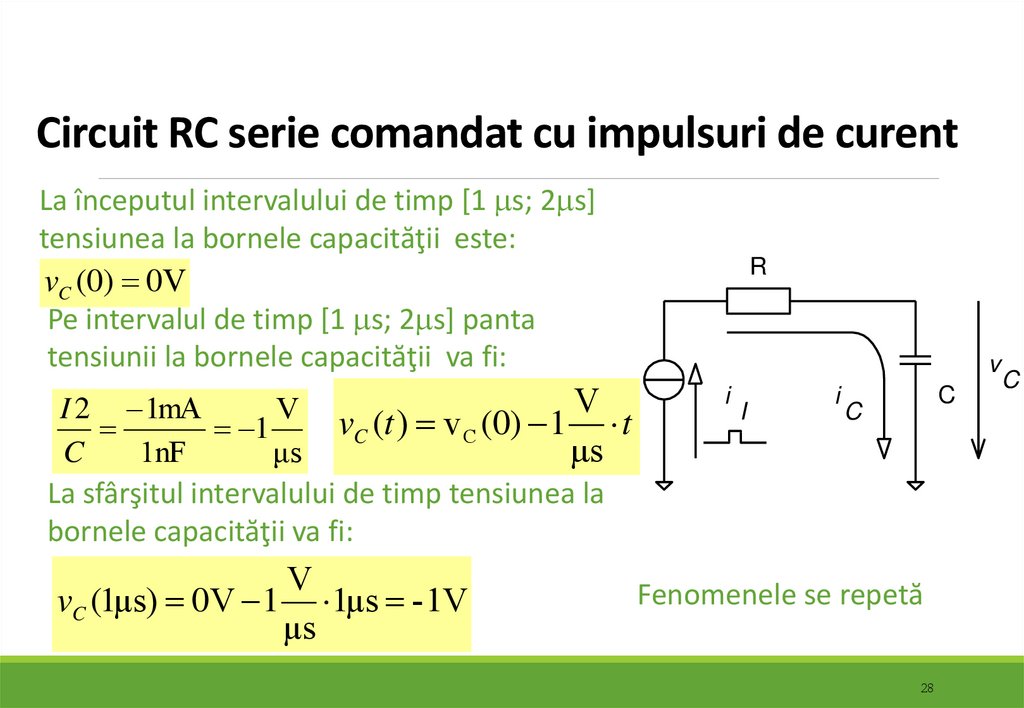
28. Circuit RC serie comandat cu impulsuri de curent

La începutul intervalului de timp [1 s; 2 s]
tensiunea la bornele capacităţii este:
vC (0) 0V
Pe intervalul de timp [1 s; 2 s] panta
tensiunii la bornele capacităţii va fi:
V
I 2 1mA
V
vC (t ) v C (0) 1 t
1
μs
C
1nF
μs
La sfârşitul intervalului de timp tensiunea la
bornele capacităţii va fi:
V
vC (1μs) 0V 1 1μs -1V
μs
R
v
i
I
i
C
C
Fenomenele se repetă
28
C

29. Circuit RC serie comandat cu impulsuri de curent

R
k
1
C
[nF]
1
I1[mA]
1
T1
s
1
I2[mA]
-1
T2
s
1
Vc(0)
-1
t
Vc(0)
T1
-1
T1+T2
2T1+T2 1.00
2T1+2T2
3T1+2T2 1.00
4T1+3T2
4T1+4T2 1.00
5T1+4T2
5T1+5T2 1.00
6T1+5T2
6T1+6T2 1.00
T
1
1
1
1
1
1
1
1
1
1
1
1
-1
1
-1
1
-1
1
-1
1
-1
1
C
1
1
1
1
1
1
1
1
1
1
1
Vc(t)
0
-1
0
-1
0
-1
0
-1
0
-1
0
29

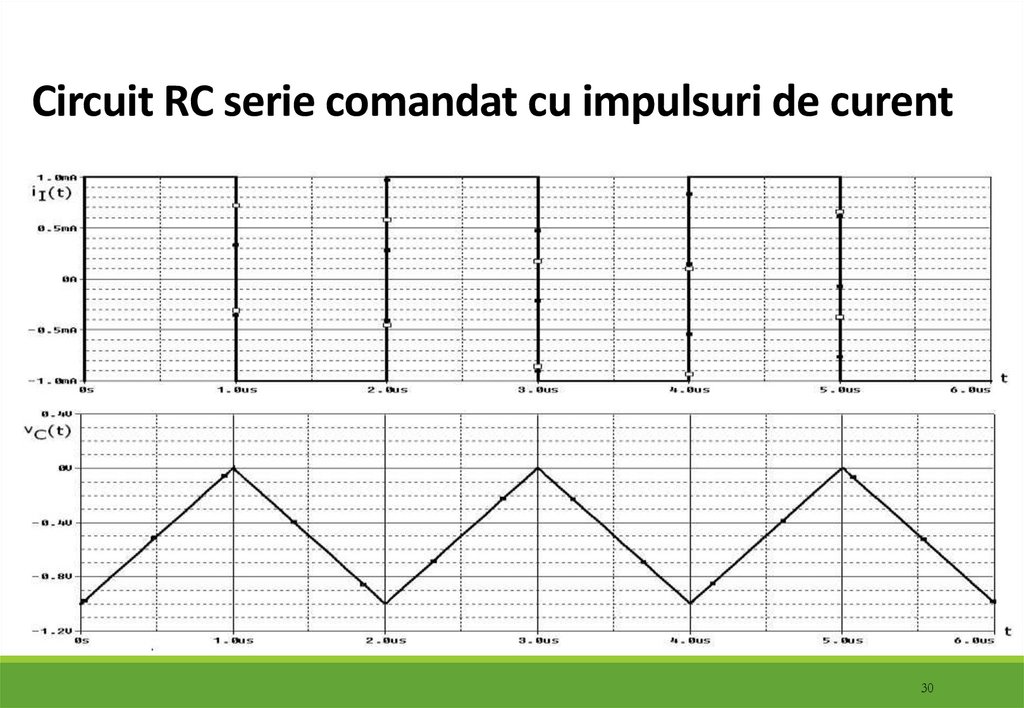
30. Circuit RC serie comandat cu impulsuri de curent

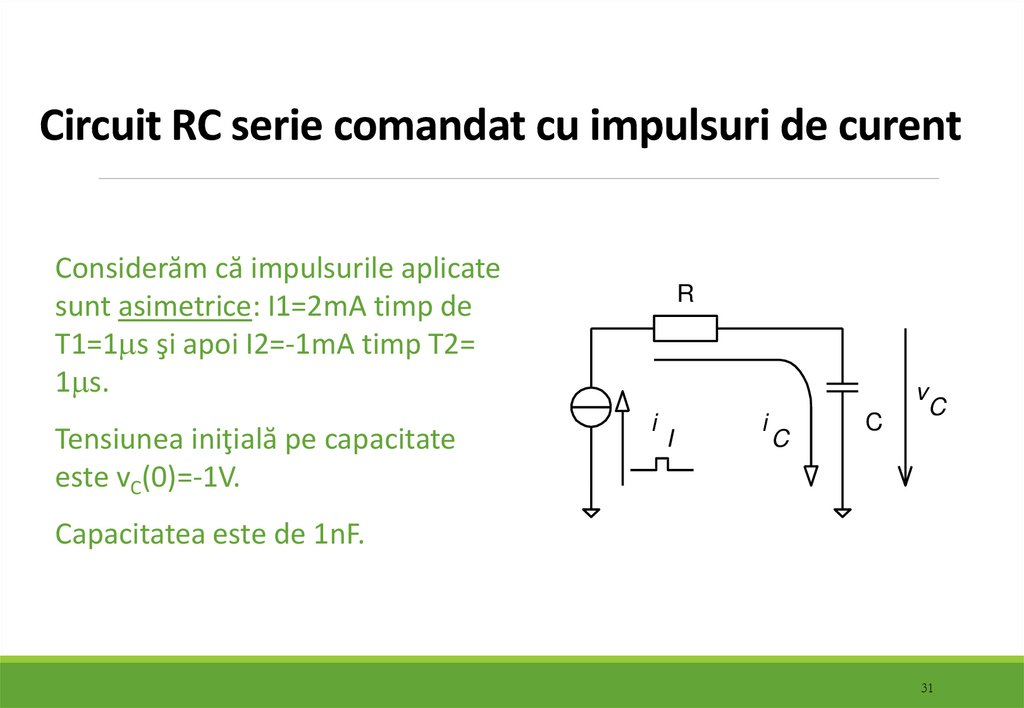
30

31. Circuit RC serie comandat cu impulsuri de curent

Considerăm că impulsurile aplicate
sunt asimetrice: I1=2mA timp de
T1=1 s şi apoi I2=-1mA timp T2=
1 s.
Tensiunea iniţială pe capacitate
este vC(0)=-1V.
R
v
i
I
i
C
C
C
Capacitatea este de 1nF.
31

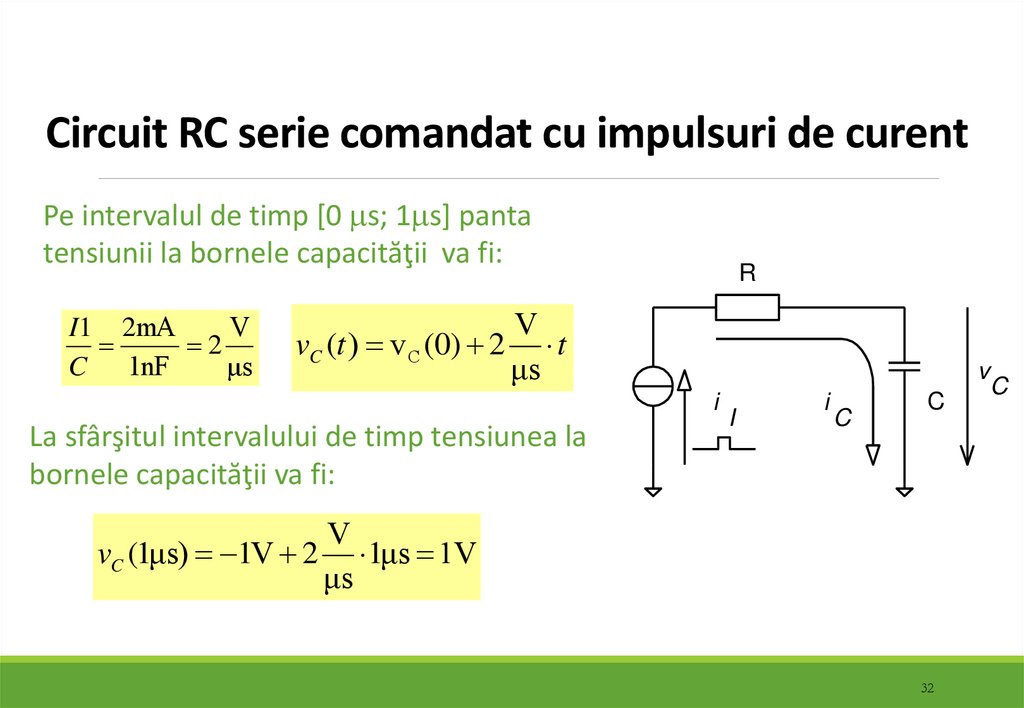
32. Circuit RC serie comandat cu impulsuri de curent

Pe intervalul de timp [0 s; 1 s] panta
tensiunii la bornele capacităţii va fi:
I1 2mA
V
2
C 1nF
μs
R
V
vC (t ) v C (0) 2 t
μs
v
i
La sfârşitul intervalului de timp tensiunea la
bornele capacităţii va fi:
I
i
C
C
V
vC (1μs) 1V 2 1μs 1V
μs
32
C

33. Circuit RC serie comandat cu impulsuri de curent

La începutul intervalului de timp [1 s; 2 s]
tensiunea la bornele capacităţii este:
vC (0) 1V
Pe intervalul de timp [1 s; 2 s] panta
tensiunii la bornele capacităţii va fi:
I 2 1mA
V
1
C
1nF
μs
V
vC (t ) v C (0) 1 t
μs
La sfârşitul intervalului de timp tensiunea la
bornele capacităţii va fi:
V
vC (1μs) 1V 1 1μs 0V
μs
R
v
i
I
i
C
C
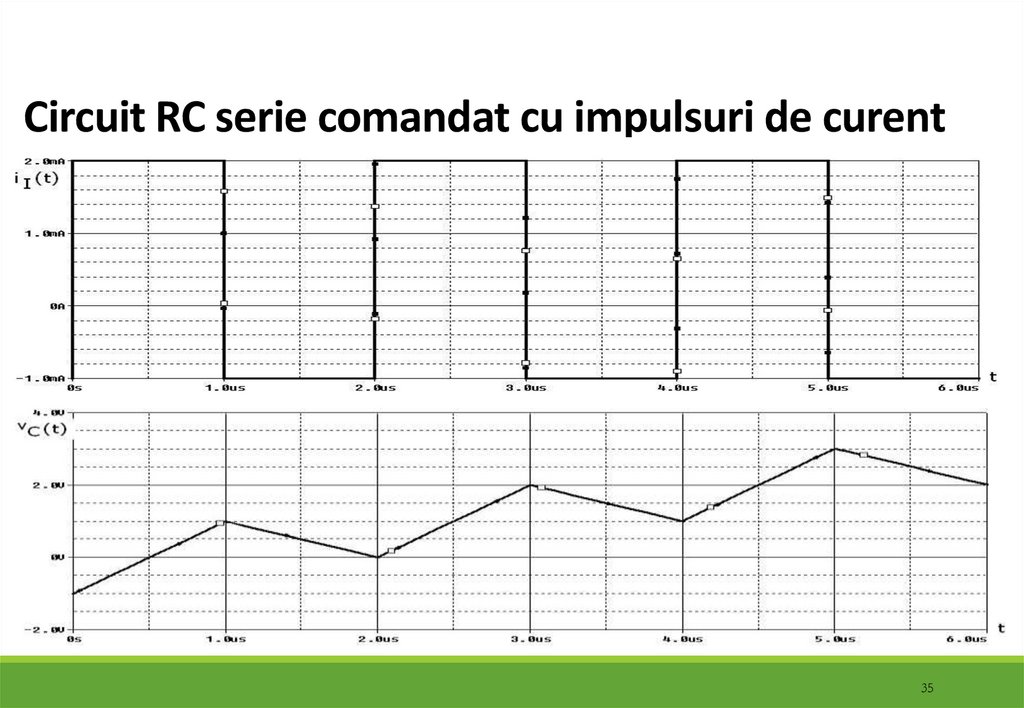
Fenomenele se repetă,
dar tensiunea creşte
continuu!!!!!
33
C

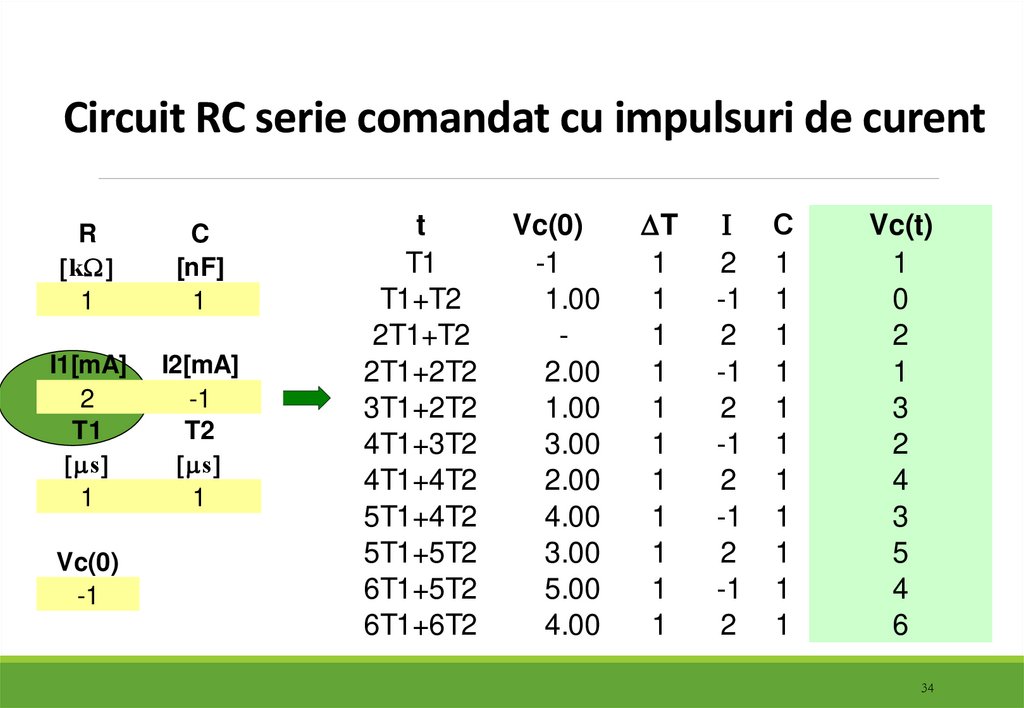
34. Circuit RC serie comandat cu impulsuri de curent

R
k
1
C
[nF]
1
I1[mA]
2
T1
s
1
I2[mA]
-1
T2
s
1
Vc(0)
-1
t
T1
T1+T2
2T1+T2
2T1+2T2
3T1+2T2
4T1+3T2
4T1+4T2
5T1+4T2
5T1+5T2
6T1+5T2
6T1+6T2
Vc(0)
-1
1.00
2.00
1.00
3.00
2.00
4.00
3.00
5.00
4.00
T
1
1
1
1
1
1
1
1
1
1
1
2
-1
2
-1
2
-1
2
-1
2
-1
2
C
1
1
1
1
1
1
1
1
1
1
1
Vc(t)
1
0
2
1
3
2
4
3
5
4
6
34

35. Circuit RC serie comandat cu impulsuri de curent

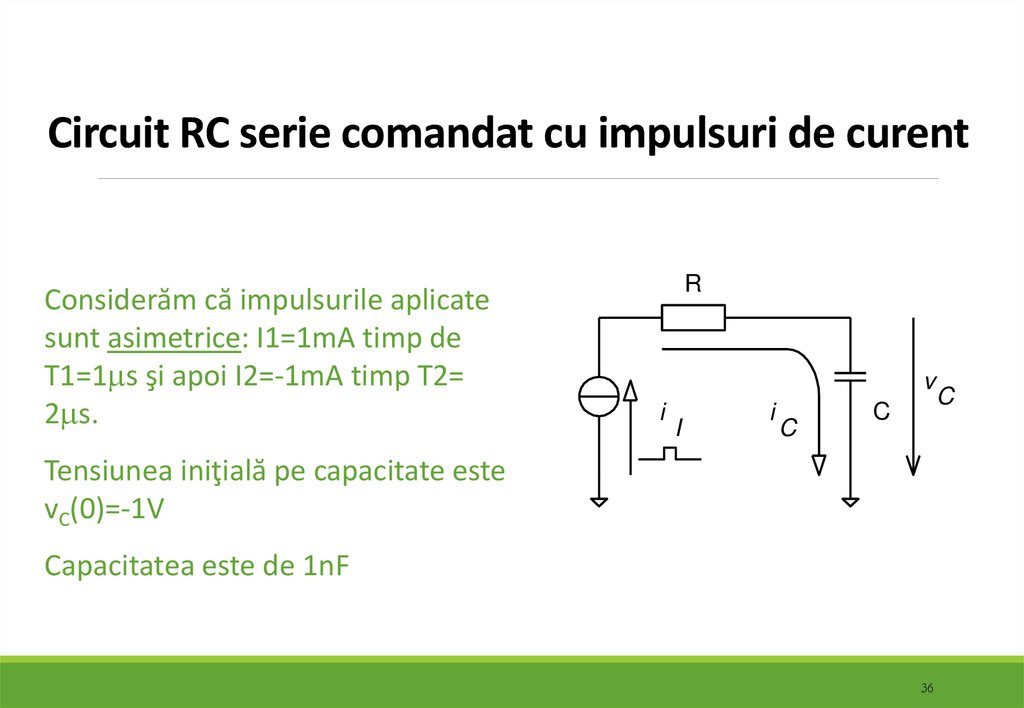
35

36. Circuit RC serie comandat cu impulsuri de curent

Considerăm că impulsurile aplicate
sunt asimetrice: I1=1mA timp de
T1=1 s şi apoi I2=-1mA timp T2=
2 s.
R
v
i
I
i
C
C
Tensiunea iniţială pe capacitate este
vC(0)=-1V
Capacitatea este de 1nF
36
C

37. Circuit RC serie comandat cu impulsuri de curent

Pe intervalul de timp [0 s; 1 s] panta
tensiunii la bornele capacităţii va fi:
R
I1 1mA
V
1
C 1nF
μs
V
vC (t ) v C (0) 1 t
μs
La sfârşitul intervalului de timp tensiunea la
bornele capacităţii va fi:
v
i
I
i
C
C
V
vC (1μs) 1V 1 1μs 0V
μs
37
C

38. Circuit RC serie comandat cu impulsuri de curent

La începutul intervalului de timp [1 s; 3 s]
tensiunea la bornele capacităţii este:
vC (0) 0V
Pe intervalul de timp [1 s; 3 s] panta
tensiunii la bornele capacităţii va fi:
I 2 1mA
V
1
C
1nF
μs
R
v
i
I
i
C
C
V
vC (t ) v C (0) 1 t
μs
La sfârşitul intervalului de timp tensiunea la
bornele capacităţii va fi:
V
vC (1μs) 0V 1 2μs -2V
μs
Fenomenele se repetă,
dar tensiunea scade
continuu!!!!!
38
C

39. Circuit RC serie comandat cu impulsuri de curent

R
k
1
C
[nF]
1
I1[mA]
1
T1
s
1
I2[mA]
-1
T2
s
2
Vc(0)
-1
t
Vc(0)
T1
-1
T1+T2
2T1+T2 2.00
2T1+2T2 1.00
3T1+2T2 3.00
4T1+3T2 2.00
4T1+4T2 4.00
5T1+4T2 3.00
5T1+5T2 5.00
6T1+5T2 4.00
6T1+6T2 6.00
T
1
2
1
2
1
2
1
2
1
2
1
1
-1
1
-1
1
-1
1
-1
1
-1
1
C
1
1
1
1
1
1
1
1
1
1
1
Vc(t)
0
-2
-1
-3
-2
-4
-3
-5
-4
-6
-5
39

40. Circuit RC serie comandat cu impulsuri de curent

40