Математична модель транспортної задачі

1.

Математична модель
транспортної задачі
Математична модель транспортної задачі має такий вигляд:
m n
Z cij xij min;
(5.1)
i 1 j 1
за обмежень
xij ai i 1, m ;
(5.2)
xij b j j 1, n ;
(5.3)
n
j 1
m
i 1
xij 0 i 1, m; j 1, n ,
(5.4)
де хij — кількість продукції, що перевозиться від і-го
постачальника до j-го споживача; сij — вартість перевезення
одиниці продукції від і-го постачальника до j-го споживача; аi —
запаси продукції і-го постачальника; bj — попит на продукцію jго споживача.
1

2.

Я к щ о в т р а н с п о р т н і й з а д а ч і з а г а л ьн а к і л ьк і с т ь
продукції постачальників дорівнює загальному
попиту всіх споживачів, тобто
m
n
i 1
j 1
ai b j ,
(5.5)
то таку транспорту задачу називають збалансованою, або
закритою. Якщо ж така умова не виконується, то транспортну
задачу називають незбалансованою, або відкритою.
2

3.

Визначення оптимального плану транспортних задач з обмеженнями.
1. Хай з a1 в b j перевезення заборонене, тоді тариф cij M , де M позитивна величина набагато більш ніж всі тарифи перевезень. Такий підхід
називається блокування клітки або заборона перевезень.
2. Хай з a1 в b j потрібно перевезти рівно
клітку (i, j ) записується
d ij одиниць вантажу. Тоді в
число d ij , після чого клітинку вважають вільною з
максимально великим тарифом M .
3. Хай з a1 в b j повинно бути заведено не менше d ij одініць вантажу. В
цьому випадку рахують і запаси a1 та потреби b j менше на задану величину.
Далі знаходять оптимальний план поставленої транспортної задачі. Тоді
оптимальний план вихідного значення буде більше отриманого на d ij * cij .
4. Хай з a1 в b j перевозиться не більше ніж d ij одиниць вантажу. На
підставі цього вихідного значення ставиться додаткова задача.
У таблиці вихідних даних для кожного j -го обмеження передбачимо
додатковий стовпець b' j . До кожного обмеження привласнимо додатковий
стовпець. У цьому стовпці тарифи призначаються такі ж як і в стовпці j ,
окрім i -го рядка, в цьому рядку тариф призначається M .Потреби
пункту b j вважаються d ij , а потреби додаткового стопця призначаються
рівними b' j b j d ij . Задачу можна розв'язати, якщо для неї можна побудувати
опорний план.
3

4.

Приклад
Три пункти відправлення і 5 пунктів призначення. По запасах: 160, 90,
140. По потребах: 90, 60, 80,70, 90. З пункту
в пункт
повинно прийти
не менше 50 одиниць товару, з пункту
в пункт
повинно прийти не
менше 60 одиниць товару,а з пункту
в пункт
повинно прийти не
більше 40 одиниць товару.
4

5.

A
j
B
j
B1
A1
B2
5
90
B3
3
10
A2
7
A3
8
B4
2
4
8
4
160-50
5
3
1
M
90
5
5
30
140-60
20
2
30
70-30
90-60
10
6
70
90
9
60-50
B'4
B5
20
4
80
30
F1=90*5+3*10+2*10+5*70+3*20+5*20+2*30+5*30=1220
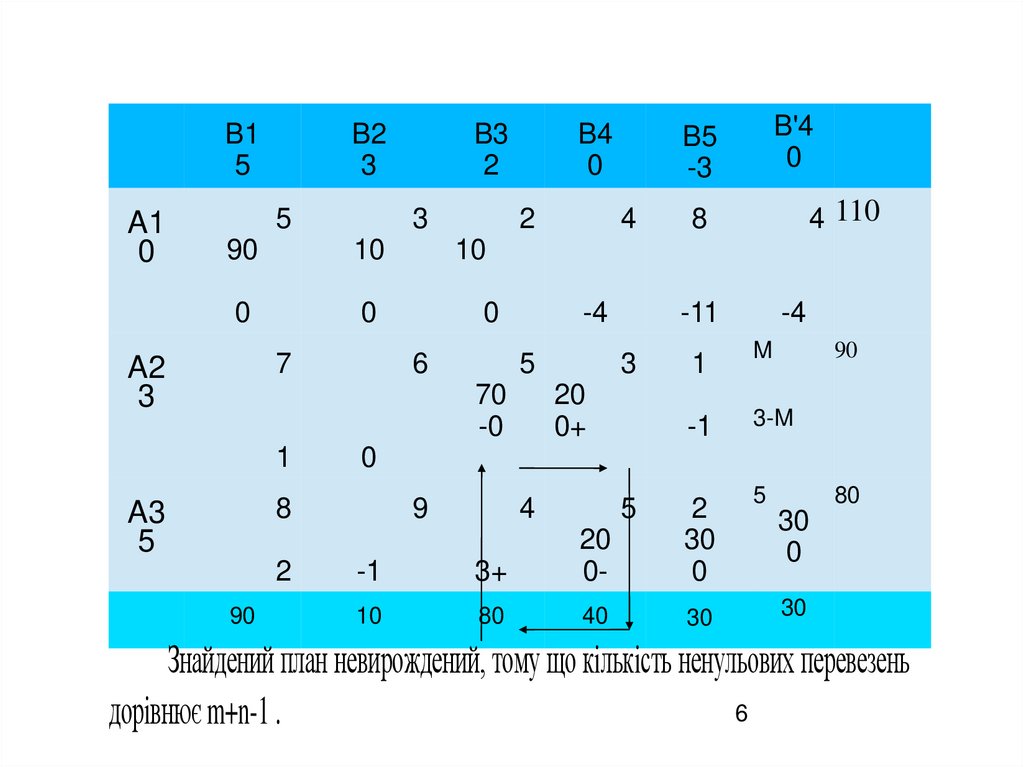
Знайдений план невирождений, тому що кiлькiсть ненульових перевезень
дорiвнює m+n-1 .
5

6.

B1
5
A1
0
B2
3
5
3
90
10
0
0
7
A2
3
B3
2
B4
0
2
0
6
2
90
4 110
8
-4
5
-11
3
20
0+
1
-1
-4
M
90
3-M
0
8
A3
5
4
10
70
-0
1
B'4
0
B5
-3
9
4
5
-1
3+
20
0-
10
80
40
2
30
0
30
5
80
30
0
30
Знайдений план невирождений, тому що кiлькiсть ненульових перевезень
6
дорiвнює m+n-1 .

7.

B1
5
A1
0
B2
3
5
3
90
10
0
0
7
A2
3
B3
2
B4
0
2
0
6
-1
90
4 110
8
-4
5
-8
3
40
0
1
4+
-1
M
90
6-M
0
8
A3
2
4
10
50
-0
1
B'4
3
B5
0
9
4
5
-4
20
+0
5
2
30
0-
10
80
40
30
5
80
30
0
30
Знайдений план невирождений, тому що кiлькiсть ненульових
перевезень
7
дорiвнює m+n-1 .

8.

9.

B1
5
A1
0
B2
3
5
B3
2
3
2
90-
10
10+
0
0
0
7
+
A2
3
1
6
-1
90
4
5
3
40
0
4
4 110
8
-10
1
30
0
0
9
B'4
3
B5
-2
-4
200
8
A3
2
B4
0
5
2
-4
50
+0
-3
-2
10
80
40
30
-1
M
90
6-M
5
80
30
0
30
Знайдений план невирождений, тому що кiлькiсть ненульових перевезень
9
дорiвнює m+n-1 .

10.

B1
5
A1
0
B2
3
5
3
70
10
0
0
7
20
A2
2
B3
2
B4
1
2
0
6
-3
-1
90
4 110
8
5
-9
3
40
0
9
4
1
-1
M
90
5-M
30
0
-1
8
A3
2
4
30
-1
0
B'4
3
B5
-1
5
2
-4
50
0
-2
-1
10
80
40
30
5
30
0
30
F5=5*70+3*10+2*30+7*20+3*40+1*30+4*50+5*30=1080
F=F5+50* +60* =1080+50*3+60*2=1350
80
10

English Русский Rules