Свойства прямой и обратной функций

1.

Функция у = f (х) называется монотонной на
множестве Х, если она на этом множестве или
убывает или возрастает.

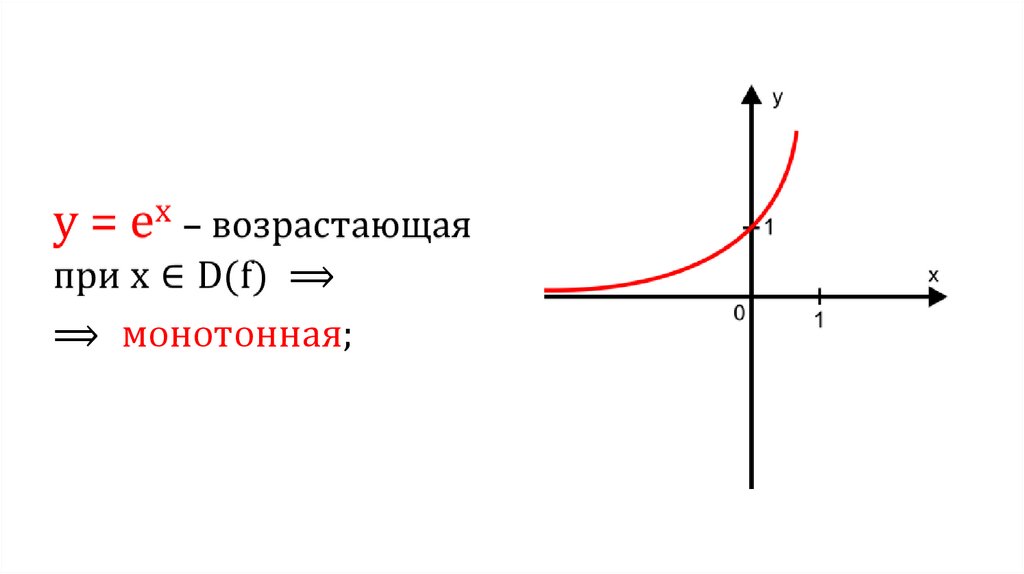
2.

⟹
⟹ монотонная;

3.

Если функция у = f(х), х ∈ Х принимает любое свое
значение только в одной точке множества Х, то
функцию называют обратимой.

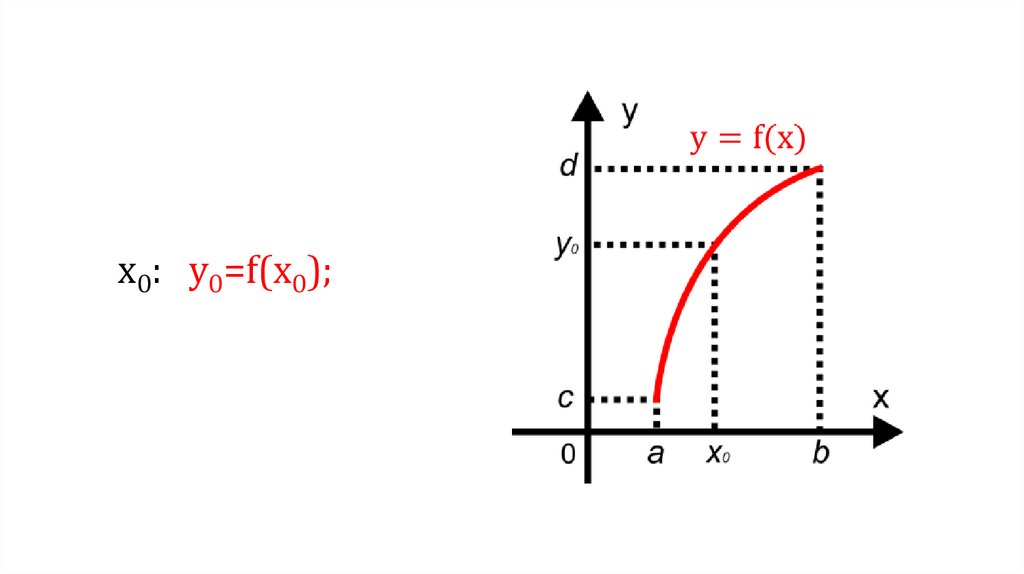
4.

х0: у0=f(х0);

5.

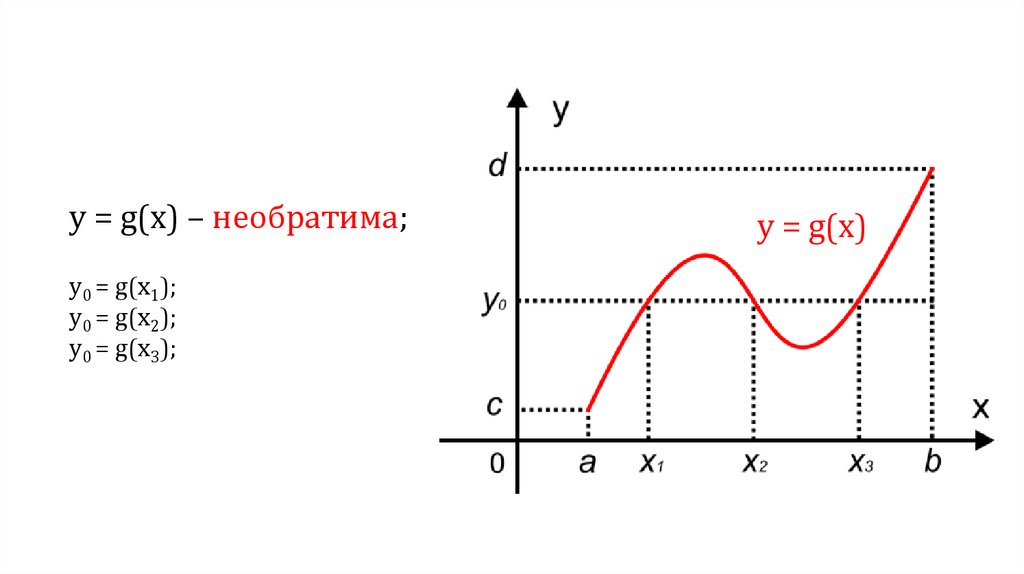
у = g(х) – необратима;
у0 = g(х1);
у0 = g(х2);
у0 = g(х3);
у = g(х)

6.

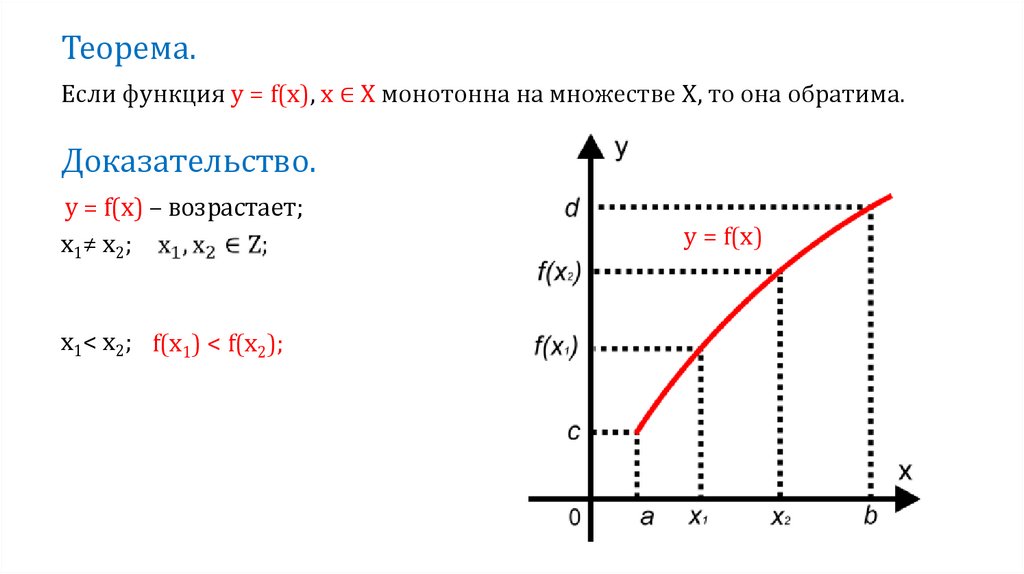
Теорема.
Если функция y = f(x), х ∈ Х монотонна на множестве Х, то она обратима.
Доказательство.
y = f(x) – возрастает;
х1≠ х2;
х1< х2; f(х1) < f(х2);
y = f(x)

7.

y = f(x) – обратимая функция;
определена на множестве Х;
Е(f) = Y;
x = f –1(y) – обратная функция;
определена на множестве Y;
Е(f) = X;

8.

Свойства прямой и обратной функций:
1. Область определения функции у = f(х):
Х является областью значений функции x = f -1(y).
2. Область значения функции у = f(x):
Y является областью определения функции x = f -1(y).
3. Если функция у = f(х) возрастает (убывает) на множестве Х,
то функция x = f -1(y) возрастает (убывает) на множестве У,
где У – область значений функции у = f(х).

9.

у = f(х) – возрастающая функция;
у1 =f(х1) ; у2 = f(х2) ; х1 < х2 – единственные;
х1 ≥ х2; ⟹
f(х1) ≥ f(х2) ;
у =f(х)– возрастающая; ⟹
у1≥ у2;
у1< у2;
х1 < х2; x = f -1(y) возрастает на У;

10.

Пример 1. Показать, что для функции y = 3x – 2 существует обратная
функция, и найти ее аналитическое выражение.
Решение.
Линейная функция y = 3x – 2, E(f) = R;
x2>x1 ⟹ 3x2>3x1 ⟹ 3x2 –2 > 3x1 –2 ⟹ y2 > y1
y = 3x – 2 – возрастающая;
у0: 3х – 2 = у0 ⟹ х0=
у0 и х0 – единственная пара;
y = 3x – 2 – обратима;

11.

Решение.
y = x²— квадратичная функция;
D(у) = R;
убывает на (-∞;0];
возрастает на [0;∞);
на промежутке [0;∞) – монотонна;
x² = у;

12.

Пример 3. Найти обратную функцию к функции у = х3.
Решение.
D(у) = R;

13.

Замечание:
монотонность функции, является достаточным
условием существования обратной функции.
Но оно не является необходимым условием.

14.

Алгоритм нахождения обратной функции:
1. Убедиться, что функция монотонна.
2. Выразить переменную х через у.
3. Переобозначить переменные.
Вместо х=f –1(y) пишут y=f –1(x);