Начала комбинаторики. Перестановки

1. Начала комбинаторики

Перестановки
К.Ю. Поляков, Е.А. Ерёмин, 2013
Презентацию подготовила Покровская Анастасия
(студентка 1-го курса Мурманского колледжа искусств,
отд. Живопись ) по материалам Н.А.Резник, Н.М. Ежовой
2018
Рук. Ежова Н.М.
http://kpolyakov.spb.ru

2.

2. Перестановки
ПЕРЕСТАНОВКИ – это соединения,
составленные из одних и тех же элементов,
и отличающиеся только порядком их
расположения.
Pn
ОБОЗНАЧЕНИЕ
Информационная
схема
К.Ю. Поляков, Е.А. Ерёмин, 2013
!
Буква P читается как
перестановка,
индекс n - количество
её элементов.
http://kpolyakov.spb.ru

3.

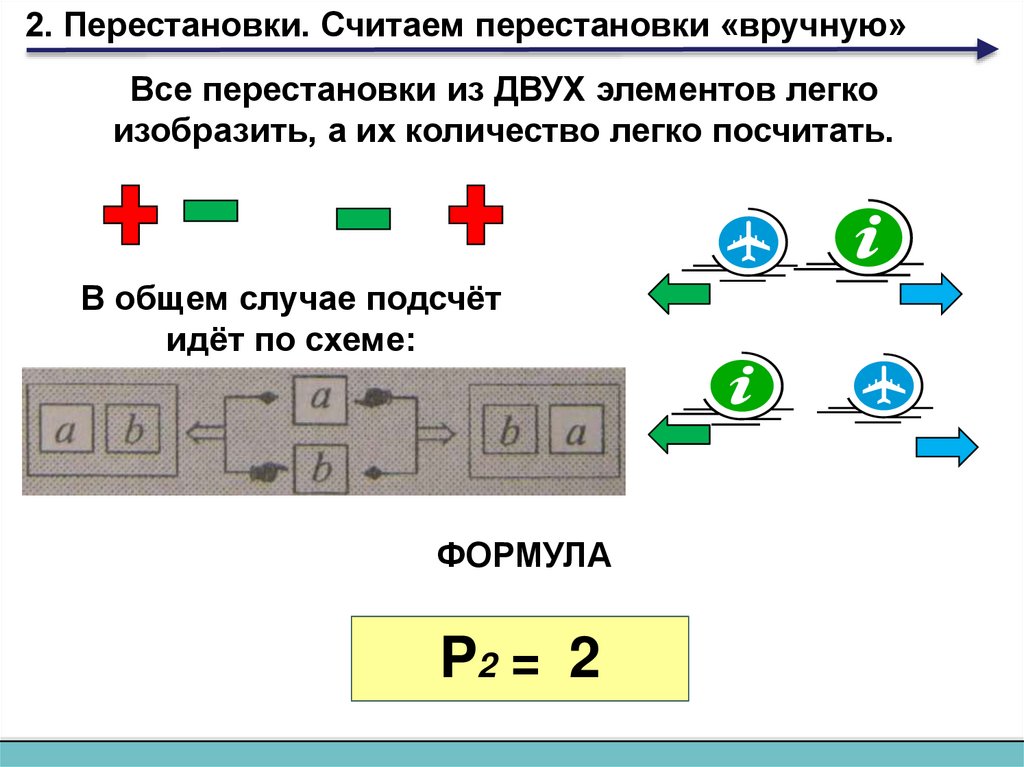
2. Перестановки. Считаем перестановки «вручную»
Все перестановки из ДВУХ элементов легко
изобразить, а их количество легко посчитать.
В общем случае подсчёт
идёт по схеме:
ФОРМУЛА
P2 = 2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

4.

2. Перестановки. Считаем перестановки «вручную»
Все перестановки из ТРЁХ элементов изобразить
легко, но их количество посчитать сложнее.
ФОРМУЛА
P3 = 6
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

5.

2. Перестановки. Считаем перестановки «вручную»
Сколько есть способов
разложить 3 цветных
карандаша в ряд?
Ответ: Р3=6
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

6. Для каждого из ЧЕТЫРЕХ элементов можно образовать перестановки из оставшихся трех элементов

2. Перестановки. Считаем перестановки «вручную»
Число перестановок из ЧЕТЫРЕХ элементов
Для каждого из
ЧЕТЫРЕХ
элементов можно
образовать
перестановки из
оставшихся трех
элементов
1
P3 6
3
P3 6
2
Число
перестановок
из ЧЕТЫРЕХ
элементов
P3 6
P4
4
К.Ю. Поляков, Е.А. Ерёмин, 2013
P3
4
6
4
P3 6
24
http://kpolyakov.spb.ru

7.

2. . Перестановки. Считаем перестановки «вручную»
Число перестановок из ПЯТИ элементов
P4
24
P4
P5
24
5 P4
К.Ю. Поляков, Е.А. Ерёмин, 2013
P4
24
5 24
P4
24
P4
24
120
http://kpolyakov.spb.ru

8.

2. Перестановки. Выводим формулу перестановок
Вспомним и продолжим:
PP11 1
P0=1
=?
P4 P3PP
*4 44 24
1
*
2
*3*4 24
P2 PР
* 2 1 *2 2
P212
P3
P1
P5 P4 *5 1
*2
*3
*
4
*
5
24
*
5
120
P
120
P55
P3 P
*2*3 6 P4
PР332 *63 1
P2
P6 P5 *6 1
*
2*
3*
4
*P56* 6720
120*6 720
P5
И так далее…
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

9.

2. Перестановки. Выводим формулу перестановок
P6 720 P5 *6
P7 P6 *7 720*7 5040
Обобщим:
Pn Pn 1 *n
Покажем:
Обозначим
(n 1) k
Pk Pk 1 *k
Pn 1 Pn 2 *(n 1)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

10.

2. Перестановки. Выводим формулу (Факториал)
Pn Pn 1 *n Pn 2 *(n 1) *n
P0 * *n 1*1*2 * *n
Pn n!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

11.

2. Перестановки
ПЕРЕСТАНОВКИ – это соединения,
составленные из одних и тех же элементов,
и отличающиеся только порядком их
расположения.
n!
1 2 . . . (n-1) n
Формула перестановок
К сведению:
Pn (n-1)! n
Подумаем:
!
Буква P читается как
перестановка,
индекс n- количество
её элементов.
Почему 0!=1?
Потому, что Р0=1
К.Ю. Поляков, Е.А. Ерёмин, 2013
Pn
http://kpolyakov.spb.ru

12.

ЗАДАЧИ. ПЕРЕСТАНОВКИ
Сколько вариантов
очередности
обслуживания 4
человек имеется у
официанта?
Ответ: Р4=4!=24
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

13.

ЗАДАЧИ. ПЕРЕСТАНОВКИ
Сколькими способами можно
Окрасить в разные цвета 6 граней куба,
если имеются шесть красок различных
цветов и все грани должны быть разного
цвета?
Ответ: Р6=6!=720
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

14.

Задачи. Перестановки. Формула
Для каждого числа перестановок
Перечислите три его первых множителя
(n 2) (n 1) *n
Pn
(n 3) (n 2)*(n 1)
Pn-1
3
(n 1) n *(n 1)
Pn+1
4
(n 4) (n 3)*(n 2)
Pn-2
2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

15.

Задачи. Перестановки. Формула
Для каждого числа перестановок
Выразите его через n!
1
Pn
2 Pn-1
n!
n ( n 1)! n!
(n 1)!
n
n
3 Pn+1
(n 1)! n! (n 1)
n
!
4 Pn-2
n
(
n
1
)
(
n
2
)!
( n 2)!
n (n 1)
n (n 1)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

16.

Задания для самостоятельного выполнения
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

17.

ЗАДАЧИ. ПЕРЕСТАНОВКИ
Сколькими способами можно
Разложить 5 различных ключей по пяти
карманам, если в каждый карман кладется
только один ключ?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

18.

ЗАДАЧИ. ПЕРЕСТАНОВКИ
Пирамида составлена из 6 кубиков
разных цветов. Сколько всего
пирамид разных по расцветке можно
составить?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

19.

Задачи. Перестановки. Общий множитель
1)
2)
3)
4)
1
Pn
1
Pn
+
1
Pn+1
+
1
Pn-1
1
1
n! (n 1)!
1
1
Pn
Pn+1
(n 1) 1
n! (n 1)
1
1
Pn-1 Pn
1 n
n( n 1)!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

20.

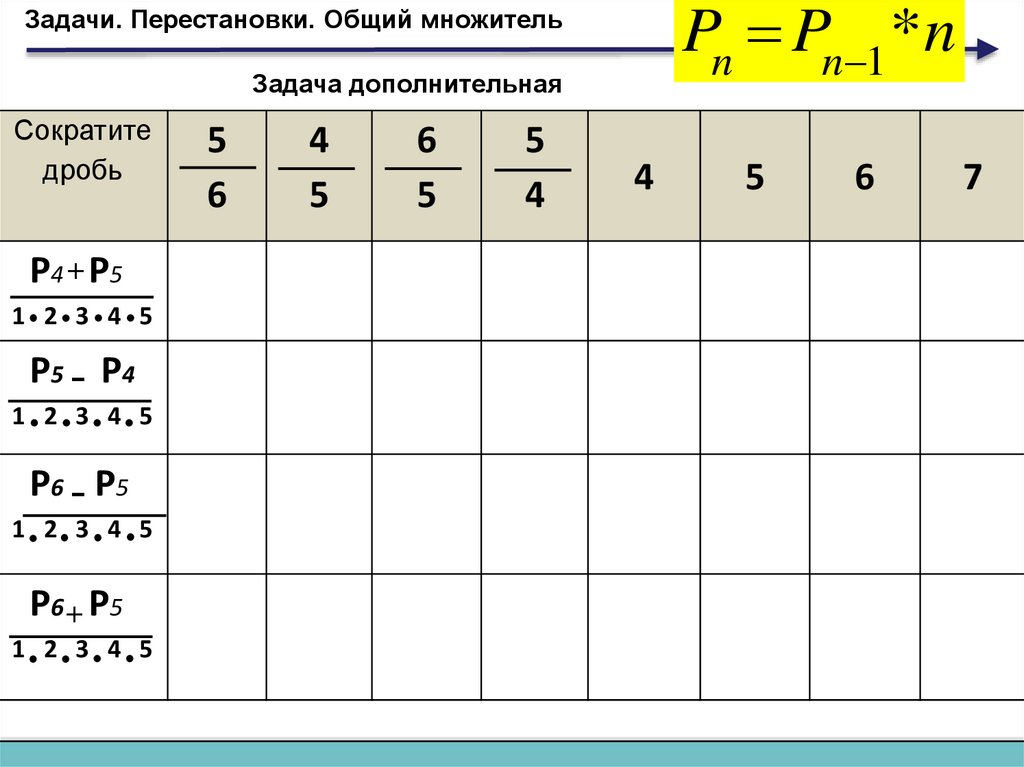
Pn Pn 1 *n
Задачи. Перестановки. Общий множитель
Задача дополнительная
Сократите
дробь
5
6
4
5
6
5
5
4
4
5
6
7
P4 + P5
1 2 3 4 5
P5 - P4
1 2 3 4 5
P6 - P5
1 2 3 4 5
P6+ P5
1 2 3 4 5
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru

21.

Дата добавления 22.09.2019
Раздел Другое
Подраздел Другое
https://www.meto
dkopilka.ru/prezent
aciya-poПросмотров
kombinatoriketemi-faktorialperestanovkiklass-87707.html
Номер
MA-087707
материала
Продолжение следует…
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru