Предельные теоремы

1.

Предельные
теоремы

2.

Теорема Пуассона
Биномиальная случайная величина с
параметрами N и p.
Пусть число N неограниченно возрастает, при этом
вероятность p = a / N , где a – const.
P ( B k )
k
CN
p 1 p
k
N k
(6.1)
Подставим p = a / N в (6.1)
N ( N 1)...( N k 1)
k!
a
N
k
a
1
N
N
a
1
N
k

3.

N ( N 1)...( N k 1) a
k!
N
k
N
a
a
1 1
N N
k
Вынесем общий множитель, не содержащий N
k
a
k!
1
2 k 1
1 N 1 N ... 1 N
N
a a
1 1
N N
Предельный переход при N
k

4.

P ( B k )
k
k
CN
p 1 p
k
N
N k
k
a a
a
a
N
1
e
N
k! N
k!
Вывод: при большом значении параметра N и
малом значении параметра p распределение
Бернулли совпадает с распределением Пуассона
Параметр распределения Пуассона
равен произведению параметров
распределения Бернулли:
a=Np

5.

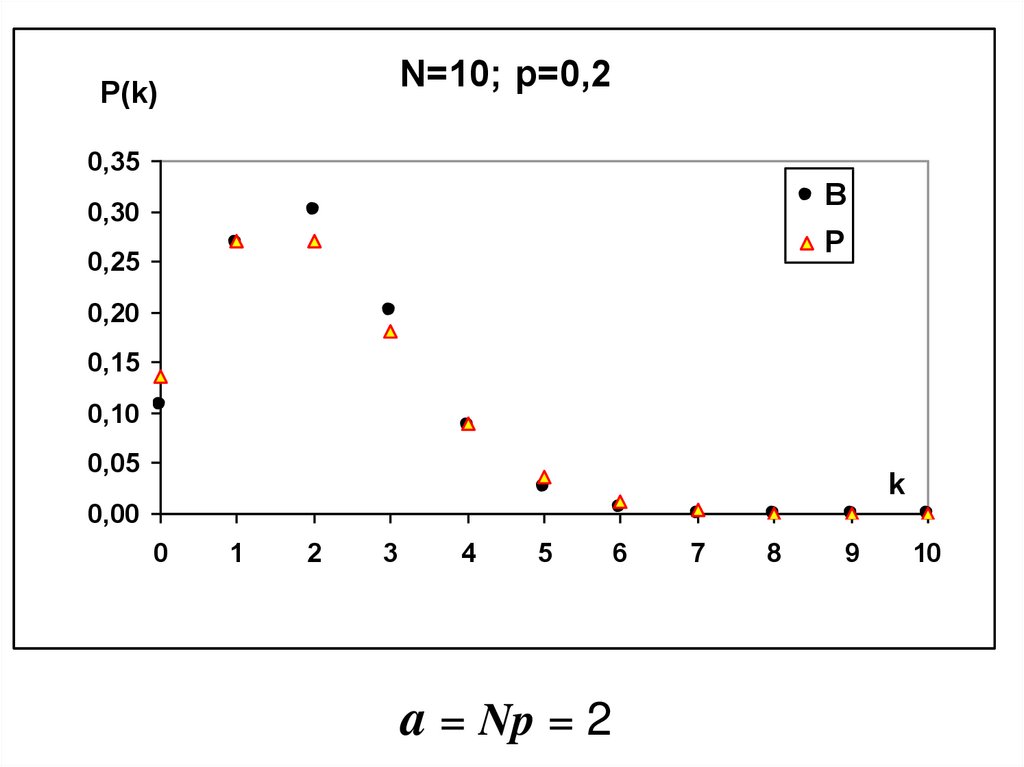
N=10; p=0,2
P(k)
0,35
B
0,30
P
0,25
0,20
0,15
0,10
0,05
k
0,00
0
1
2
3
4
5
a = Np = 2
6
7
8
9
10

6.

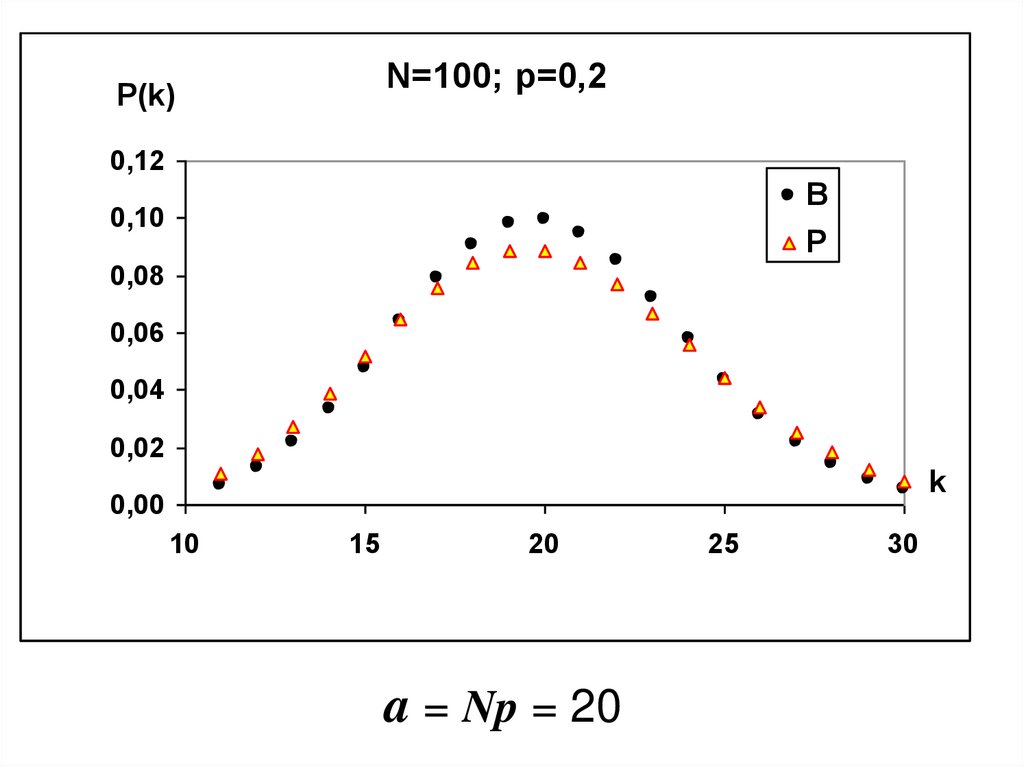
N=100; p=0,2
P(k)
0,12
B
0,10
P
0,08
0,06
0,04
0,02
k
0,00
10
15
20
a = Np = 20
25
30

7.

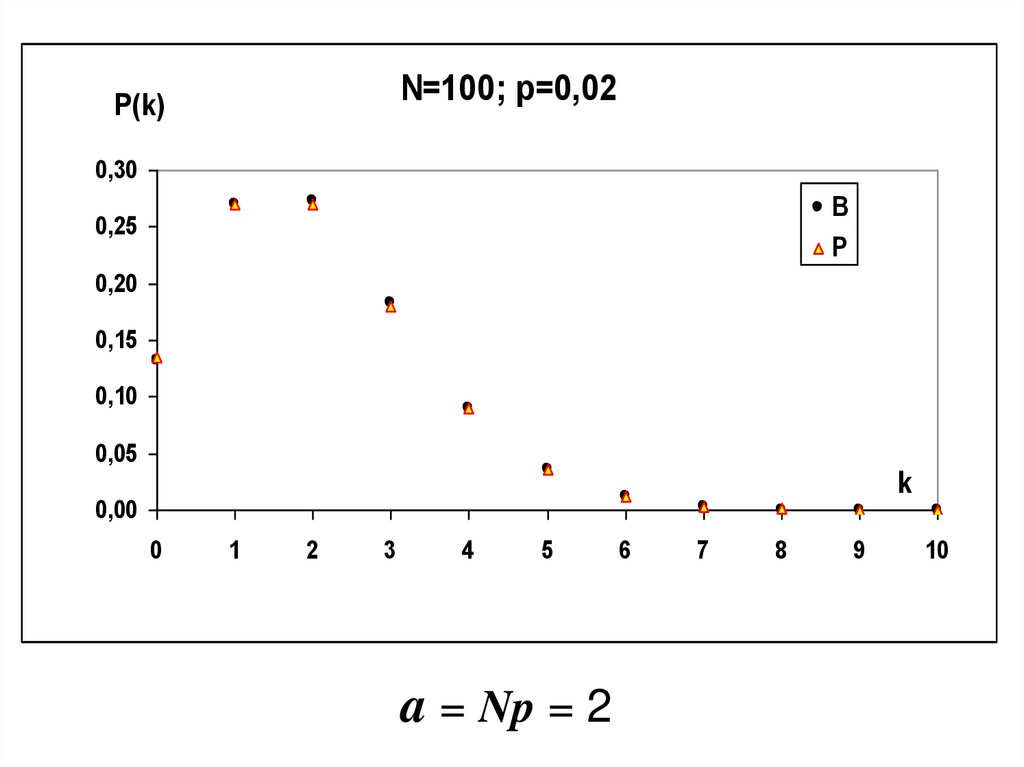
N=100; p=0,02
P(k)
0,30
B
0,25
P
0,20
0,15
0,10
0,05
k
0,00
0
1
2
3
4
5
a = Np = 2
6
7
8
9
10

8.

Хорошее совпадение распределения Бернулли
с распределением Пуассона наблюдается при
значении параметра N > 100 , и параметра
распределения Пуассона a не сильно
отличающегося от единицы.

9.

Теорема Муавра – Лапласа
Биномиальная случайная величина с
параметрами N и p.
Вероятность того, что значение этой случайной
величины k находится в интервале [k1, k2]
P k1 k k2
k k2
k
CN
p (1 p )
k
N k
k k1
Рассмотрим предельный переход при N

10.

Согласно теореме Муавра – Лапласа,
справедлив следующий предельный переход:
x2
2
1
( x )
P k1 k k2
exp
dx
2
N
2
2
x
1
где: = Np,
x1
2 = Np(1– p)
k1 Np
Np (1 p )
x2
k2 Np
Np (1 p )

11.

Это означает, что при очень больших значениях
параметра N и при большом значении
произведения параметров Np распределение
Бернулли может заменятся нормальным
(гауссовым) распределением.
Сумма вероятностей биномиальной
случайной величины заменяется интегралом
от плотности вероятности нормальной
случайной величины.
Параметр (математическое ожидание) равен
произведению Np
Параметр 2 (дисперсия) равен Np(1– p)

12.

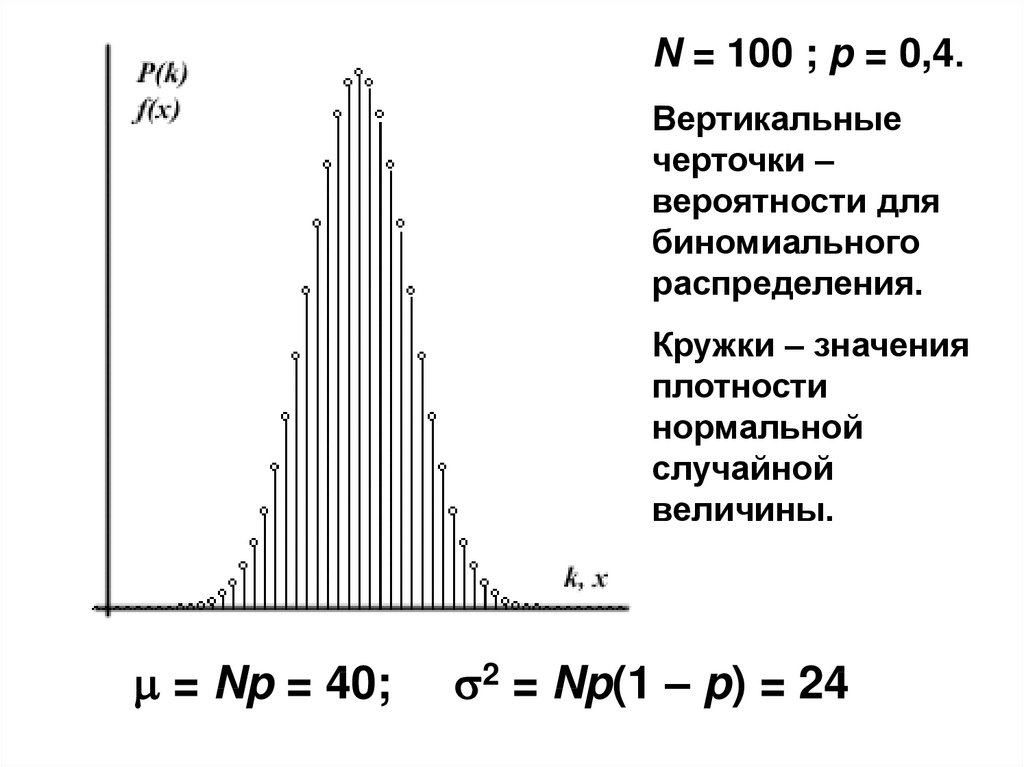
N = 100 ; p = 0,4.
Вертикальные
черточки –
вероятности для
биномиального
распределения.
Кружки – значения
плотности
нормальной
случайной
величины.
= Np = 40;
2 = Np(1 – p) = 24

13.

Как вычислить определенный интеграл в правой части
теоремы Муавра-Лапласа?
x2
2
1
( x )
exp
dx
2
2
2
x
1
Замена переменной:
z = (x – ) /
z2
z
1
exp
2
2
z
1
2
dz

14.

Функция Лапласа
x
2
1
t
( x)
exp dt
2
2
0
Интеграл с переменным верхним пределом от
нормированной функции Гаусса
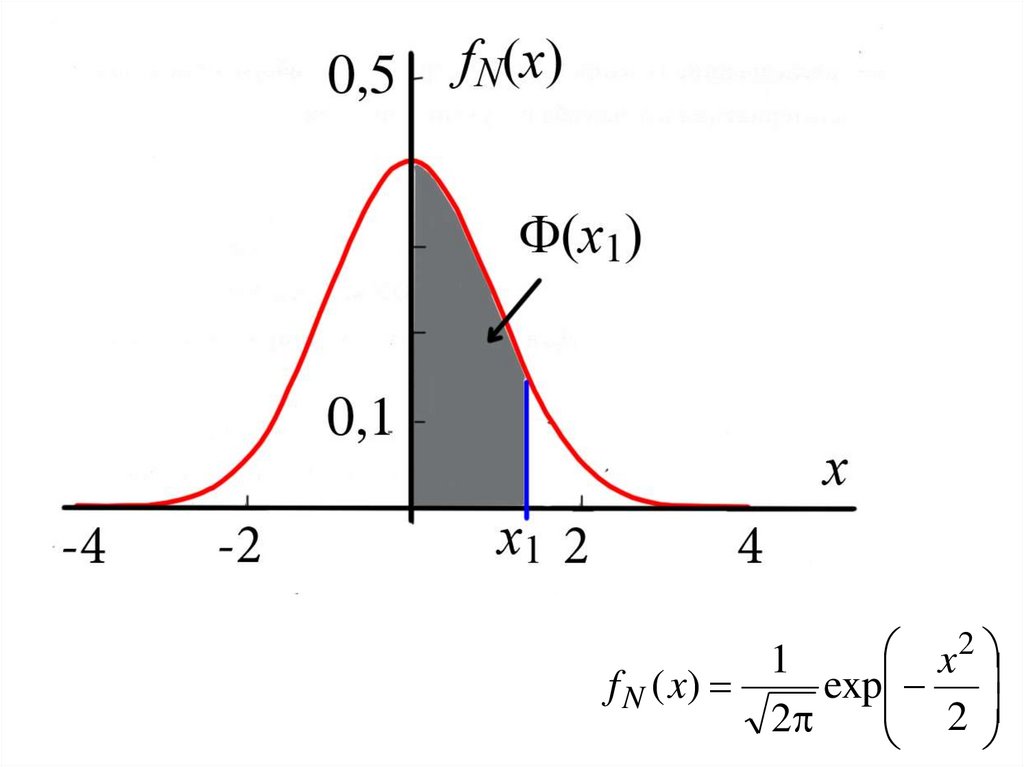
2
1
x
f N ( x)
exp
2
2
Это плотность гауссовой случайной величины
с параметрами = 0 и = 1

15.

Свойства функции Лапласа
x
2
1
t
( x)
exp dt
2
2
0
1. (x=0) = 0
2. ( x) = (x).
3. Функция Лапласа быстро стремится к 0,5.
(x = 3) = 0,49865;
(x = 5) = 0,49999997.

16.

2
1
x
f N ( x)
exp
2
2

17.

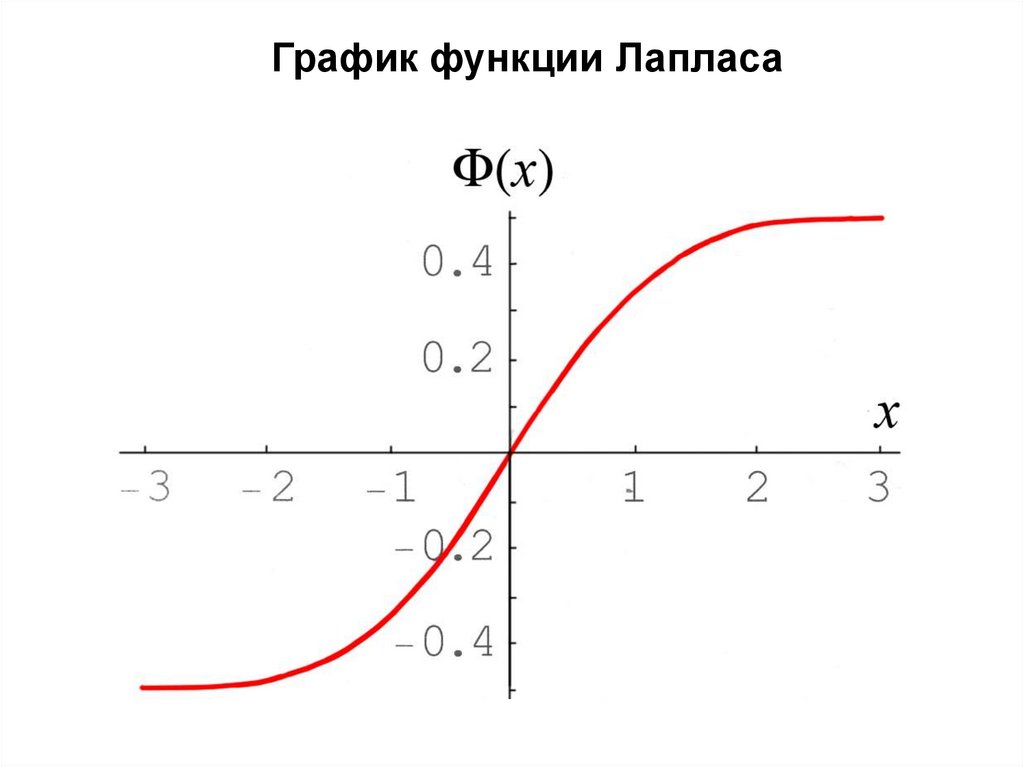
График функции Лапласа

18.

k - значение биномиальной случайной
величины с параметрами N и p.
P k1 k k2 ( x2 ) ( x1 )
где Ф – функция Лапласа, x1 и x2 – её аргументы:
x1
k1 Np
Np (1 p )
x2
k2 Np
Np (1 p )

19.

Центральная
предельная
теорема

20.

i ; (i = 1, …, N ) – случайные величины
N
N
i
i 1
Если N , то при весьма общих условиях
случайная величина N имеет нормальное
(гауссово) распределение вероятностей.

21.

Теорема 1
i ; (i = 1, …, N ) – попарно независимые случайные
величины, имеющие одинаковые распределения.
Математические ожидания M( i) = a
Дисперсии D( i) = d
N
Случайная величина
i 1
при N приобретает
нормальное распределение
с плотностью вероятности
i m / d
2
1
x
f ( x)
exp
2
2

22.

Теорема 2 (теорема Ляпунова)
i ; (i = 1, …, N ) – независимые случайные величины.
Математические ожидания M( i) = ai
Дисперсии D( i) = bi2
Конечные третьи моменты M i – ai 3 = ci
Обозначения:
N
AN
i 1
N
ai
2
BN
i 1
N
2
bi
C N2
i 1
ci2

23.

CN
lim
N BN
Если
P
N
A
i
N
i 1
BN
0
то при N
x
2
1
t
x
exp dt
N
2
2
где:
N
AN
i 1
N
ai
2
BN
i 1
2
bi
N
C N2
i 1
ci2

24.

Нормированная сумма любых независимых
случайных величин при N имеет
нормальное распределение.
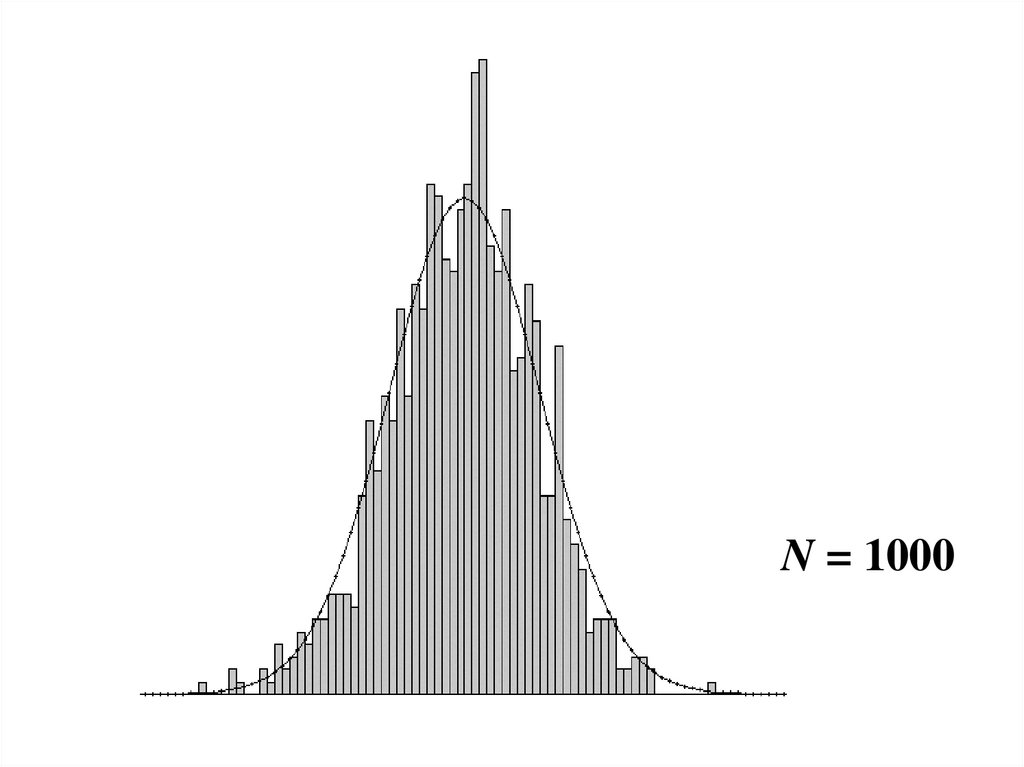
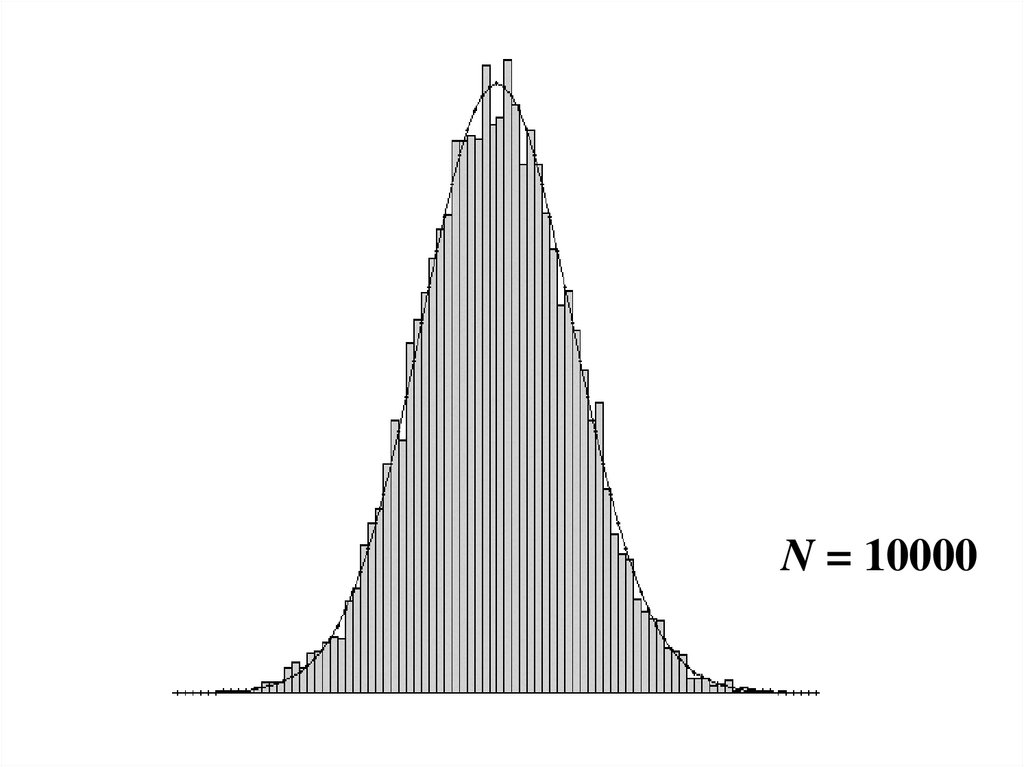
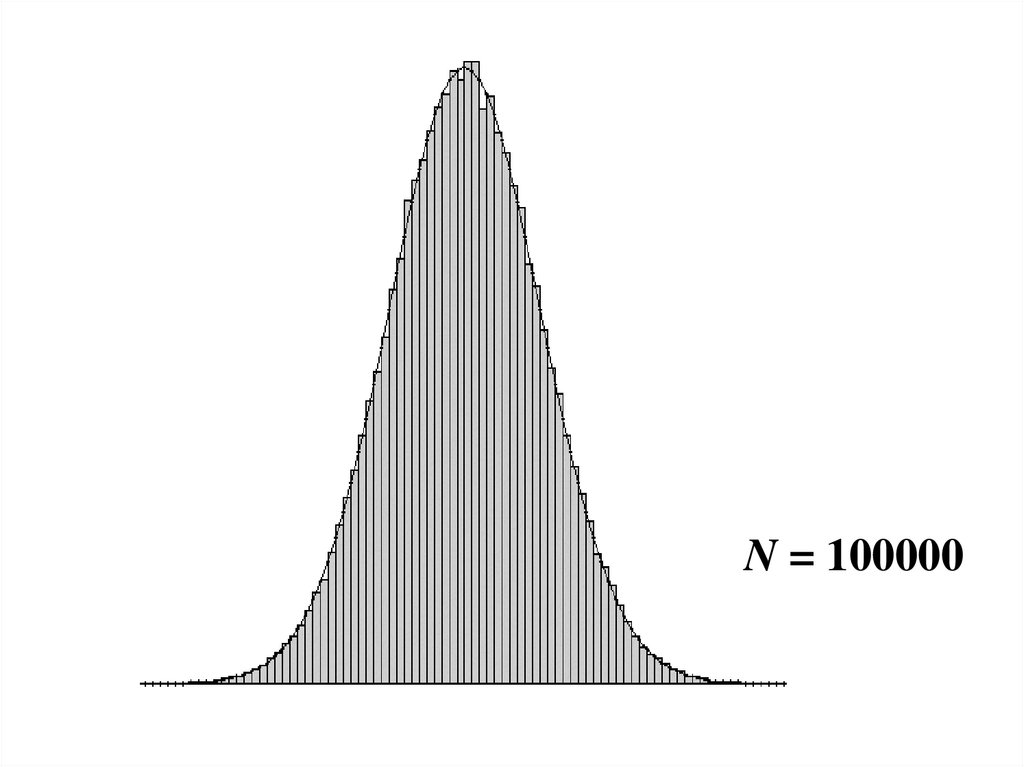
На следующих слайдах показаны графики
распределений нормированных сумма
равномерно распределенных непрерывных
случайных величин при различном количестве
слагаемых N.
Видно, что с ростом N распределение
приближается к нормальному распределению.

25.

N = 100

26.

N = 1000

27.

N = 10000

28.

N = 100000