Similar presentations:
Софизмы и парадоксы
1. Софизмы и парадоксы
Курсант СМФ, 1-ый курсБабаев Артём
2. Цели
Расширить собсвенный кругозорВыяснить как софизмы и парадоксы влияют на
человека
3. Картины с элементами нарушения логики
Мориц Эшер4. Парадокс
Парадоксом - называется суждение, которое может доказать, чтосуждение одновременно является как ложным, так и истинным.
5. Софизмы
Софизм – утверждение, являющееся ложным, но не лишенным элементалогики, за счет чего при поверхностном взгляде на него, оно кажется верным.
В отличие от парадокса, в софизме ошибка сделана специально, но скрыта,
якобы, под правильным действием.
The more you study, the more you know.
Чем больше учишься, тем больше знаешь.
The more you know, the more you forget.
Чем больше знаешь, тем больше забываешь.
The more you forget, the less you know.
Чем больше забываешь, тем меньше знаешь.
The less you know, the more you forget.
Чем меньше знаешь, тем меньше забываешь.
The less you forget, the more you know.
Но чем меньше забываешь, тем больше знаешь.
So why study?
Так для чего учиться?
6. Геометрические софизмы
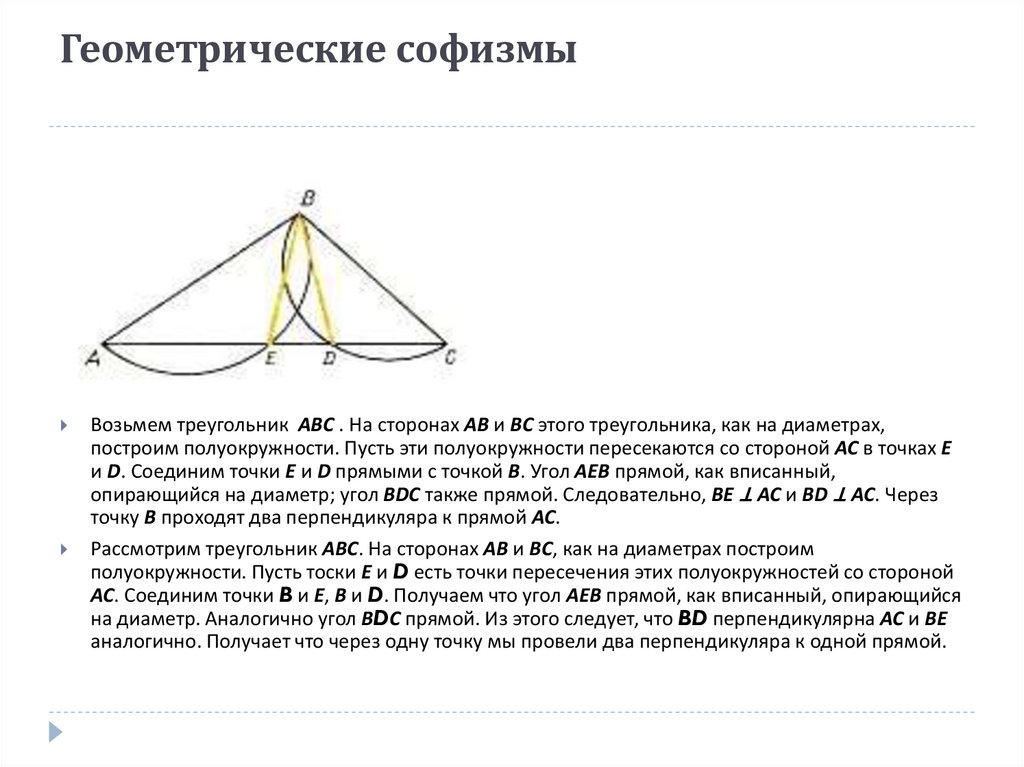
Возьмем треугольник ABC . На сторонах АВ и ВС этого треугольника, как на диаметрах,построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках Е
и D. Соединим точки Е и D прямыми с точкой В. Угол АЕВ прямой, как вписанный,
опирающийся на диаметр; угол ВDC также прямой. Следовательно, BE ⊥ AC и BD ⊥ AC. Через
точку В проходят два перпендикуляра к прямой АС.
Рассмотрим треугольник АВС. На сторонах АВ и ВС, как на диаметрах построим
полуокружности. Пусть тоски Е и D есть точки пересечения этих полуокружностей со стороной
АС. Соединим точки B и Е, В и D. Получаем что угол АЕВ прямой, как вписанный, опирающийся
на диаметр. Аналогично угол ВDС прямой. Из этого следует, что BD перпендикулярна АС и ВЕ
аналогично. Получает что через одну точку мы провели два перпендикуляра к одной прямой.
7. Ошибка
В доказательстве этого суждения, мы опирались на ошибочный чертеж. Насамом деле полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ
совпадает с ВD и наши перпендикуляры совпали. Значит, из одной точки, не
лежащей на данной прямой, нельзя опустить два перпендикуляра к этой прямой.
8. Алгебраический софизм
«Один рубль не равен ста копейкам»Тождество: если a=b, c=d, то ac=bd.
1 р.=100 коп, (1)
10р.=10*100коп.(2)
перемножая эти равенства почленно, получим
1*10 р.=100*1000 коп.
10 р.=100000 коп.
(3)
и, наконец, разделив последнее равенство на 10 получим, что
1 р.=10 000 коп.
таким образом, один рубль не равен ста копейкам.
9. Ошибка
Ошибка, состоит в нарушении правил действия с именованнымивеличинами: все действия, совершаемые над величинами, необходимо
совершать также и над их размерностями.
10. Игры с бесконечностью
Одним из первых этот парадокс сформулировал Галилео Галилей.“чётных чисел столько же, сколько натуральных”
11. Парадокс Рассела
Кроме логических, есть ещё парадоксысамоотносимости. Главный герой такого
парадокса пытается применить его условия
по отношению к самому себе. Вот какой
парадокс придумал знаменитый британский
философ и математик Бертран Рассел в
начале ХХ века, и вовсе не для развлечения,
а когда занимался одной из математических
теорий.
12.
В одной деревне был один-единственныйпарикмахер-брадобрей. Для работы ему
было установлено твёрдое правило: он
должен брить только тех жителей деревни,
которые не бреются сами. Казалось бы,
нормальное правило. Вот только у самого
брадобрея тоже растёт борода, и встал
вопрос: может ли он сам себя побрить?
Получается, что может и… не может. Посуди
сам: если он себя не бреет, значит, согласно
правилу, он себя брить может. Но если он
будет бриться сам, то опять же по правилу
он не имеет права себя брить.
13. Выводы
В первую очередь решение софизимов и парадоксов - тренировкамышления и логики человека. Человек, который разбирается в
математических головоломках, быстро и легко ориентируется в
жизненных ситуациях. Следствием от решения софизмов то, что
человек совершает меньше ошибок, а если и совершает, то с большей
вероятностью найдёт свою ошибку.











 pedagogy
pedagogy








