Вязанные вещи

1.

2.

3.

Activity
List the theoretical facts that were covered in the
last lesson.
Set goals by continuing the phrases
"Know ...".
"Understand ..."
"Know how to ...".

4.

Geometric dictation

5.

6.

7.

Rhomb
Learning objectives:
• 8 Gc.06 to know the properties and signs of
the rhombus and be able to apply them in
solving problems
Assessment The student applies the properties of the rhombus when
criteria
solving problems

8.

Terminology

9.

Research work
• draw a segment AB = 2 cm;
• draw a segment CD = 4 cm so that CD | AB,
AB∩CD=0, AO= OB, CO=OD;
• connect AC, BC, CD, AD;

10.

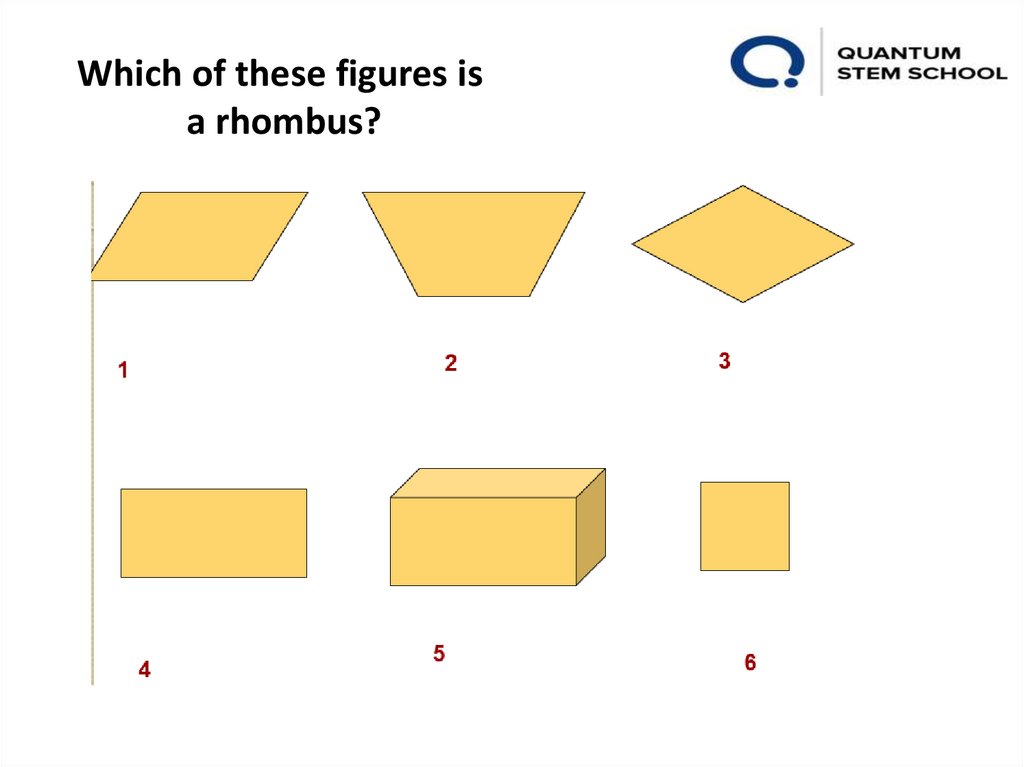
Which of these figures is
a rhombus?

11.

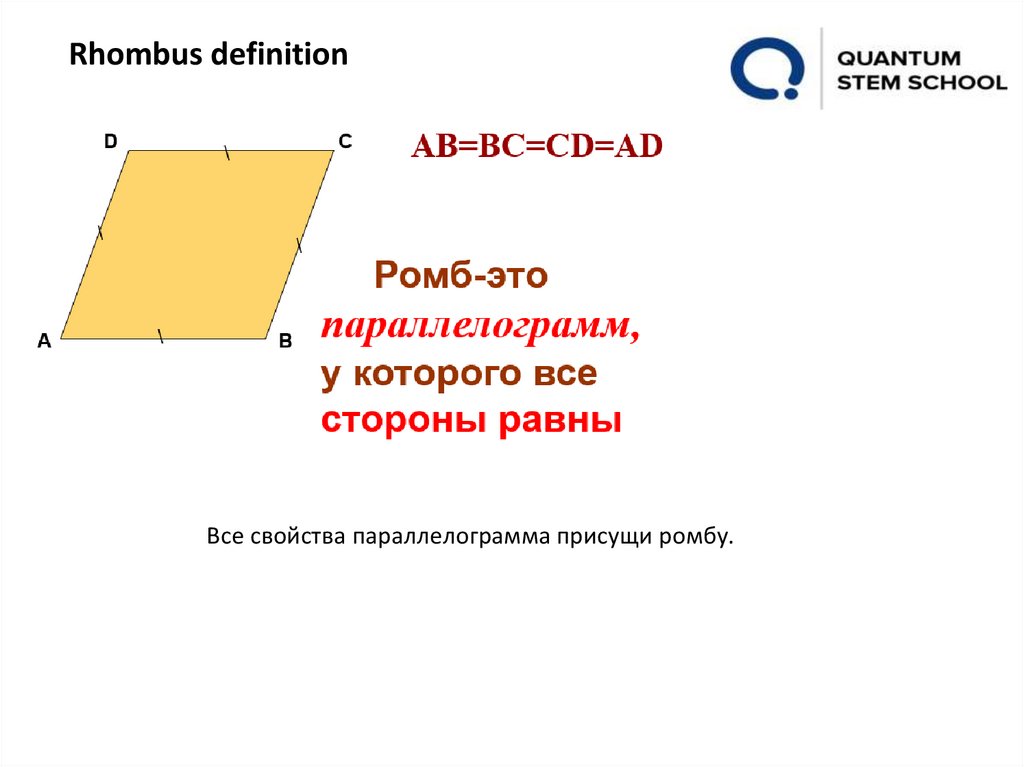
Rhombus definition
Все свойства параллелограмма присущи ромбу.

12.

A little history
• РОМБ. Заимств. в XVIII в. из франц. яз.,
где rhombe < греч. rhombos "волчок ", "кубарь" ,
"вращательное движение".
• Термин «ромб» в переводе с древнегреческого
означает «бубен».
Бубен хоть раз в жизни, но видели все.
И все знают, что он круглый.
Название масти бубны
также связанно именно
с этим фактом

13.

14.

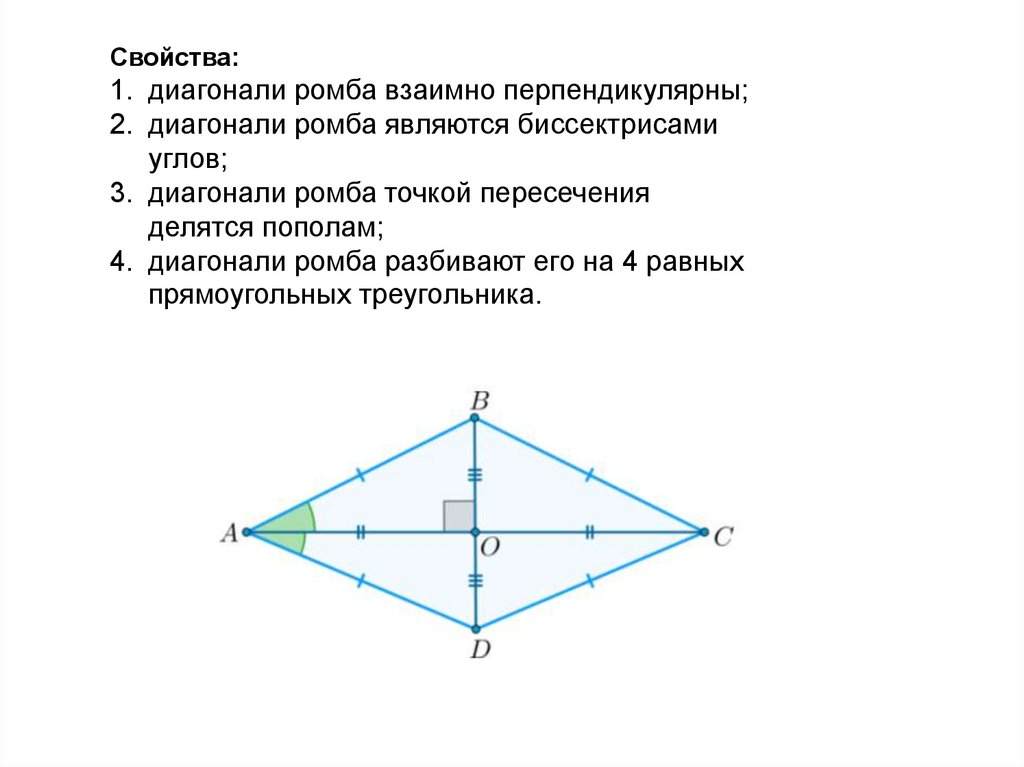
Свойства:
1. диагонали ромба взаимно перпендикулярны;
2. диагонали ромба являются биссектрисами
углов;
3. диагонали ромба точкой пересечения
делятся пополам;
4. диагонали ромба разбивают его на 4 равных
прямоугольных треугольника.

15.

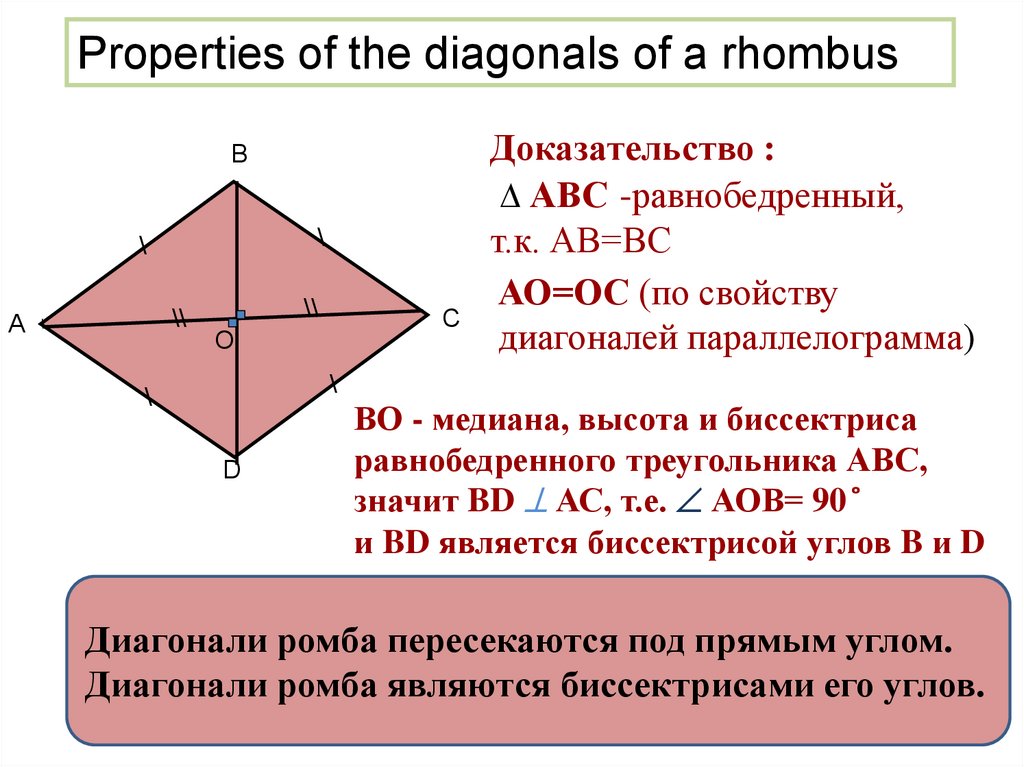
Properties of the diagonals of a rhombus
В
\
\
\\
А
\\
С
О
Доказательство :
АВС -равнобедренный,
т.к. АВ=ВС
АО=ОС (по свойству
диагоналей параллелограмма)
\
\
D
ВО - медиана, высота и биссектриса
равнобедренного треугольника АВС,
значит BD АС, т.е. АОВ= 90 ̊
и BD является биссектрисой углов B и D
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.

16.

HOW CAN YOU TELL IF YOU'RE LOOKING AT A RHOMBUS?
Signs:
if a parallelogram
1) diagonals are mutually perpendicular, then it
is a rhombus;
2) diagonals are bisectors of angles, then it is a
rhombus.
Признаки: если у параллелограмма
1.диагонали взаимно перпендикулярны, то он – ромб;
2.диагонали являются биссектрисами углов, то он – ромб.

17.

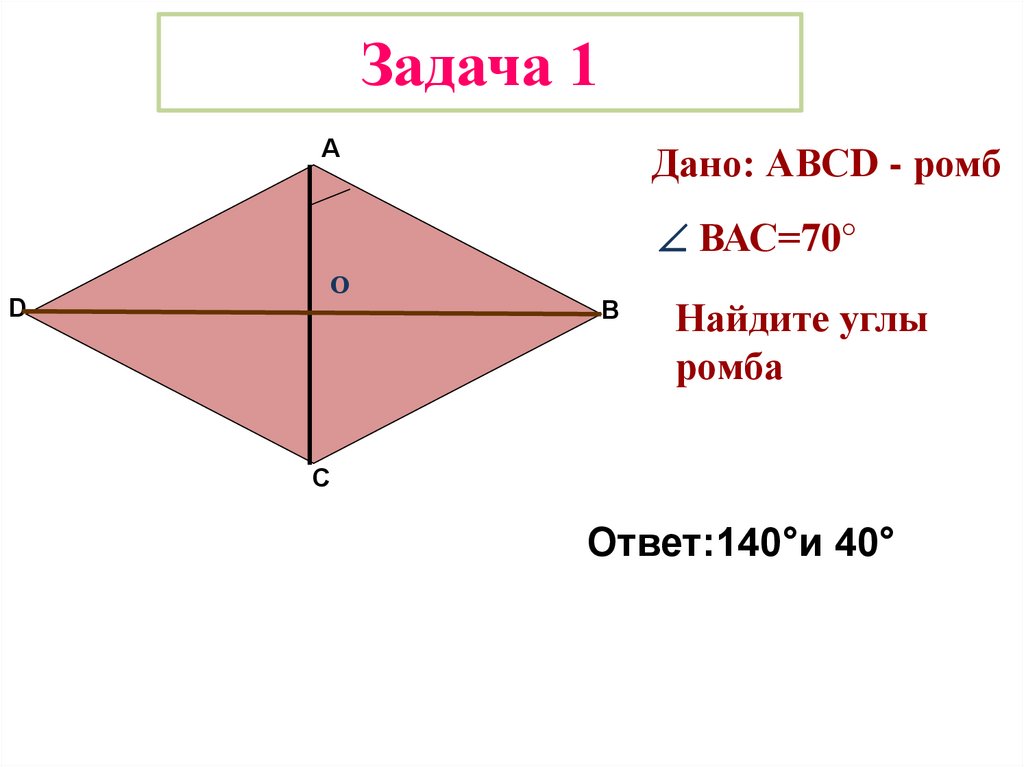
Задача 1
А
Дано: АВСD - ромб
ВАС=70°
D
О
В
Найдите углы
ромба
С
Ответ:140°и 40°

18.

Задача 2
А
Дано: АВСD – ромб
Периметр ромба равен 80 см.
Найдите сторону ромба
В
D
С
Ответ: 20 см.

19.

Тестовая работа.
Выберите номера верных утверждений
1) любой ромб является параллелограммом;
2) любой параллелограмм является ромбом;
3) диагонали ромба пересекаются под прямым углом;
4) диагонали ромба равны
5) диагонали ромба точкой пересечения делятся
пополам;
6) у ромба все углы равны;
7) параллелограмм, у которого все углы прямые
называется ромбом;
8) противолежащие стороны и противолежащие
углы ромба равны;
9)диагонали ромба являются биссектрисами его углов.

20.

Work with pairs
Задание. Разместите свойства фигур в диаграмме Эйлера-Венна и
подготовьте презентацию постерa
Например:
- Противоположные стороны параллельны/

21.

22.

Formative assessment
Descriptors
выполняет рисунок;
применяет свойства четырехугольника;
решает уравнение и записывает ответ.
применяет свойство катета в прямоугольном треугольнике
и находит длину одной стороны;
• применяет формулу периметра параллелограмма;
applies the parallelogram property;
• solves the equation and writes down the answer
• performs drawing;
• applies the property of the cathet in a right triangle and finds the
length of one side;
• applies the parallelogram perimeter formula;
• finds the length of the other side and records the answer.

23.

Individual work

24.

25.

Homework
Выучить определение ромба, его свойства и признаки