Similar presentations:
Принцип суперпозиции. Точечные заряды
1. Принцип суперпозиции. Точечные заряды
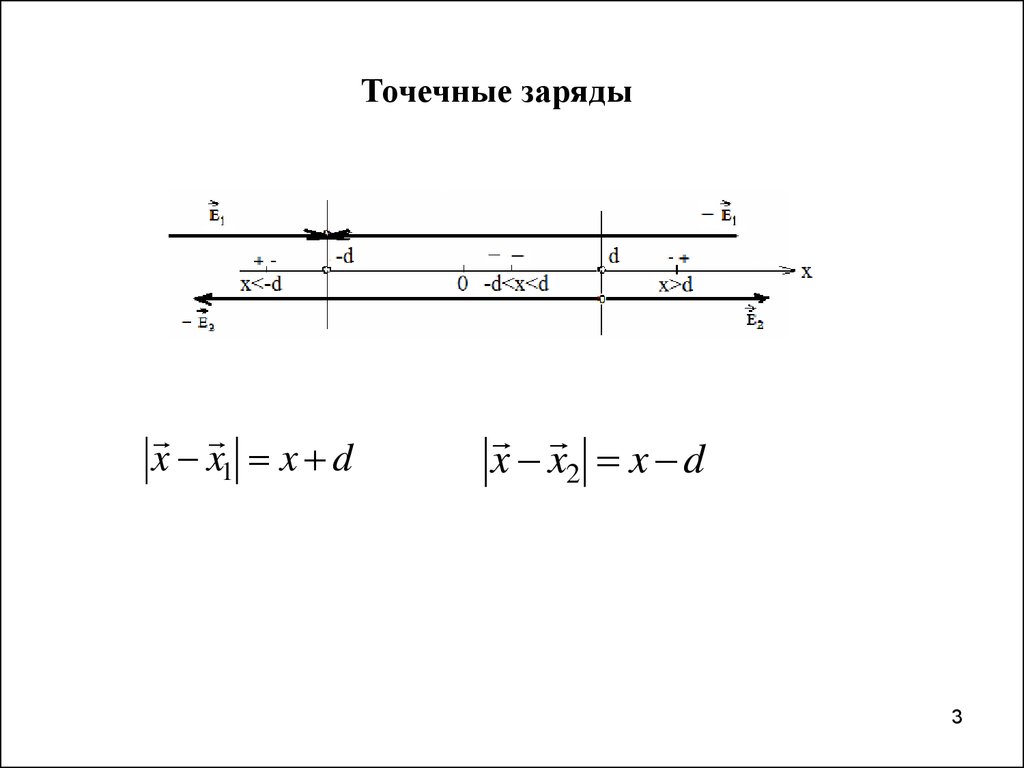
•Задача . Рассмотрим электростатическое поле, создаваемое двумяq2 , находящимися на расстоянии
точечными зарядами q1
и
друг от друга.
2d
• Пусть ось Ox совмещена с прямой, соединяющей заряды.
• Заряд q1 поместим в точку с координатой x1 d , а заряд
в точку с координатой x2 d (d 0)
.
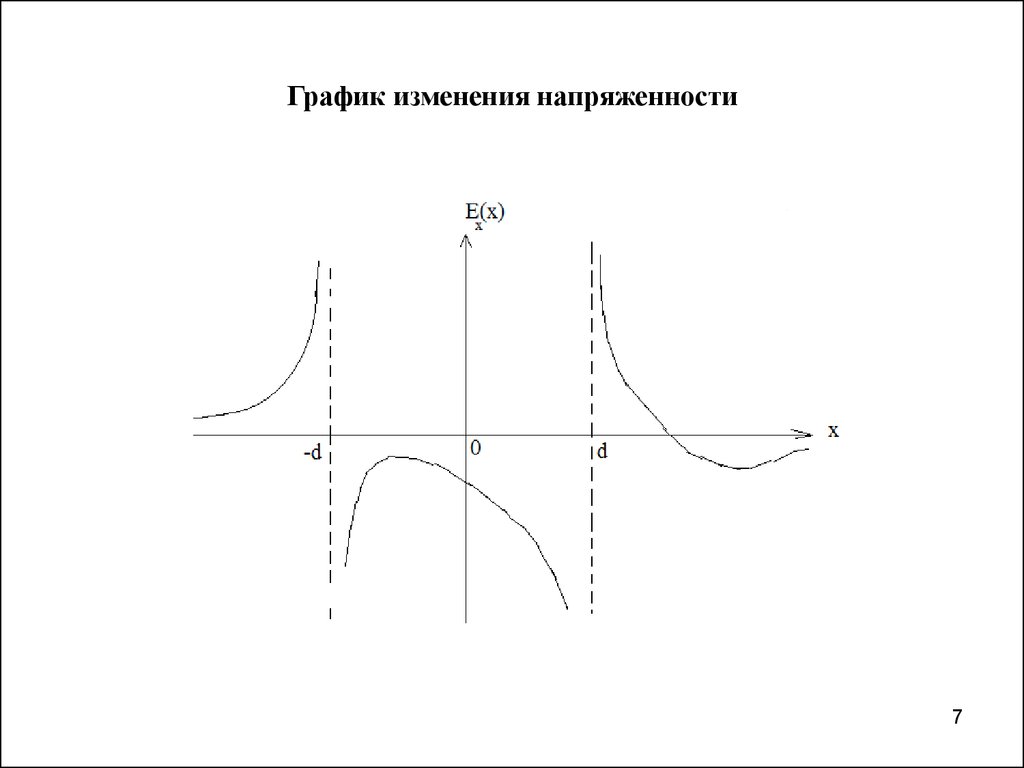
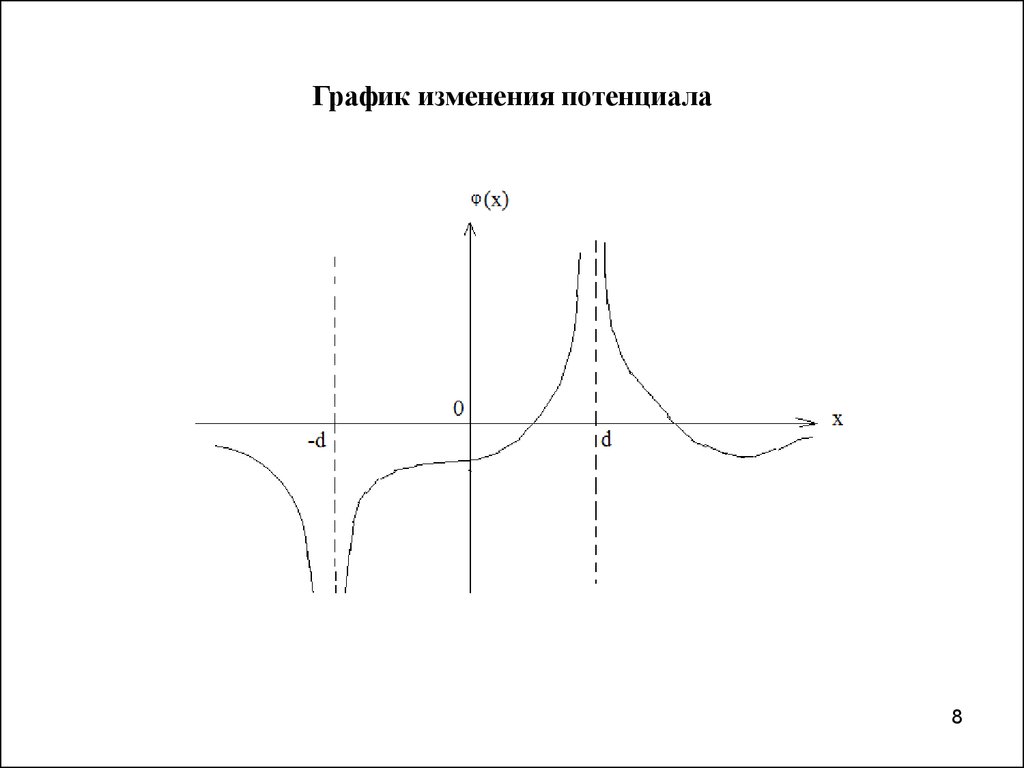
• Получить напряженность и потенциал . Построить графики
изменения напряжённости и потенциала поля вдоль оси .
q1 3q
q2 q
Решение. Известно, что точечный заряд
создаёт в точке
Кулона)
x
q2 –
q
, находящийся в точке x0 ,
следующие напряжённость и потенциал (из закона
1
q
E( x)
2
4 0 ( x x0 )
x x0
x x0
1
q
( x)
4 0 x x0
1
2. Для решения задачи будем использовать принцип суперпозиции:
1q1
E( x)
2
4 0 ( x x1 )
x x1
1
q2
2
x x1 4 0 ( x x2 )
x x2
x x2
,
1
q1
1
q2
( x)
.
4 0 x x1 4 0 x x2
2
3. Точечные заряды
x x1 x dx x2 x d
3
4. Случай 1.
x d1
3q
1
q
q x 2 4 xd d 2
E ( x ) Ex ( x)
2
2
4 0 ( x d )
4 0 ( x d )
2 0 ( x 2 d 2 )2
3q
1
q
q x 2d
( x)
4 0 x d 4 0 x d 2 0 x 2 d 2
1
Случай 2.
d x d
,
E ( x ) Ex ( x)
3q
1
q
q dx. x 2 d 2
2
2
4 0 ( x d )
4 0 ( x d )
0 ( x 2 d 2 )2
1
3q
1
q
q 2x d
( x)
4 0 (d x) 4 0 (d x) 2 0 d 2 x 2
1
4
5. Случай 3.
E ( x ) Ex ( x)x d
3q
1
q
q 4 xd x 2 d 2
2
2
4 0 ( x d )
4 0 ( x d )
2 0 ( x 2 d 2 ) 2
1
3q
1 ,q
q 2d x
( x)
,
4 0 x d 4 0 x d 2 0 x 2 d 2
1
,,
,
Некоторые вычисления
при
lim Ex ( x) 0
x
lim ( x) 0
x
.
.
x d
lim Ex ( x)
x d 0
lim ( x)
x d 0
5
6. Некоторые вычисления при
lim Ex ( x) Ex (0)x d 0
lim ( x)
x d 0
d
( x) 0 x ,
2
1
0 d 2
lim E x ( x)
q
x d 0
q
1
(0)
2 0 d
lim ( x)
x d 0
Некоторые вычисления
при
,
lim Ex ( x) 0
x d 0
Ex ( x) 0 x (2 3)d ,
x
( x ) 0 x 2d ,
x d
lim E x ( x)
x
lim ( x) 0
d x d
q x3 6dx 2 3d 2 x 2d 3
Ex ( x) 0
0
2
2 3
0
(x d )
lim ( x)
x d 0
( x) 0 x (2 3 )d
6





 physics
physics








