Similar presentations:
Краткая теория переключательных функций, основные элементы алгебры логики
1.
КРАТКАЯ ТЕОРИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ, ОСНОВНЫЕЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ.
Основные понятия алгебры логики
Джорж Буль, 19 век, «Алгебра логики»
В устройствах ЛОC сигналы принимают два состояния:
логического «0» и логической «1» при этом
если Х=1, то Х 0 и наоборот, если Х=0, то Х 1.
Высказывание - всякое утверждение относительно, которого
можно сказать, оно является «истинным» или «ложным» и
имеет значение истинности, равное соответственно либо «1»
либо «0».
Простое высказывание или логическая переменная не зависит
от истинности других высказываний.
Сложное высказывание или логическая функция - зависит от
истинности составляющих его простых высказываний
2.
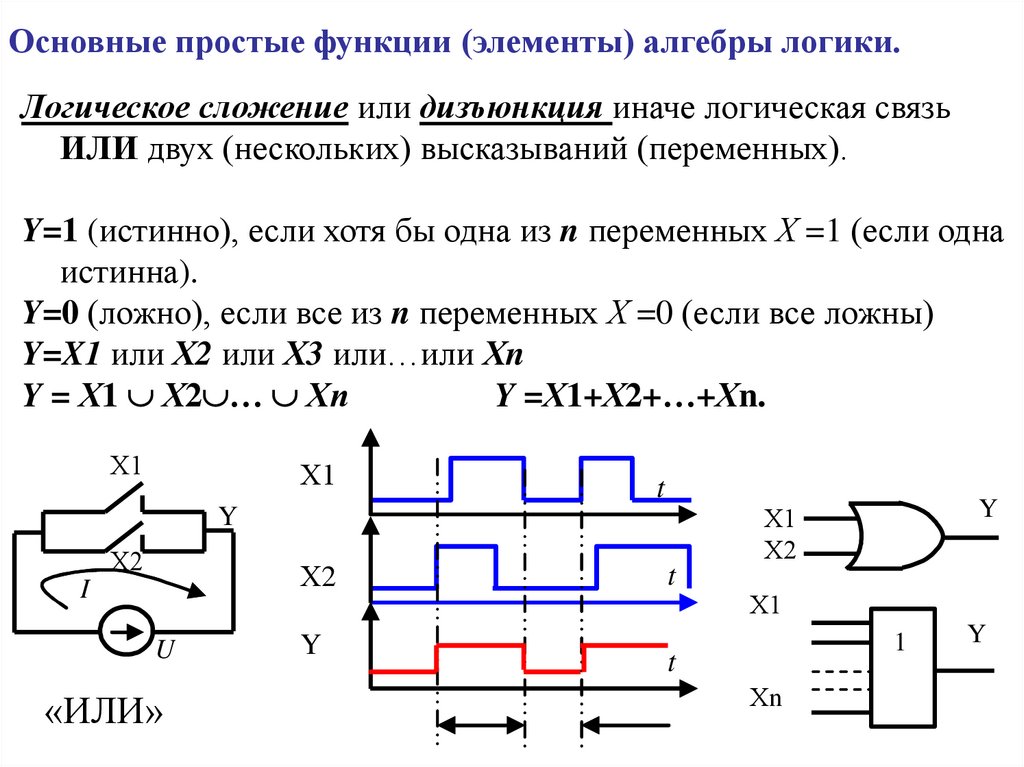
Основные простые функции (элементы) алгебры логики.Логическое сложение или дизъюнкция иначе логическая связь
ИЛИ двух (нескольких) высказываний (переменных).
Y=1 (истинно), если хотя бы одна из n переменных Х =1 (если одна
истинна).
Y=0 (ложно), если все из n переменных Х =0 (если все ложны)
Y=X1 или Х2 или Х3 или…или Хn
Y = Х1 Х2 … Хn
Y =Х1+Х2+…+Хn.
Х1
Х1
t
Х2
Х2
I
U
«ИЛИ»
Y
Y
Х1
Х2
Y
t
Х1
1
t
Хn
Y
3.
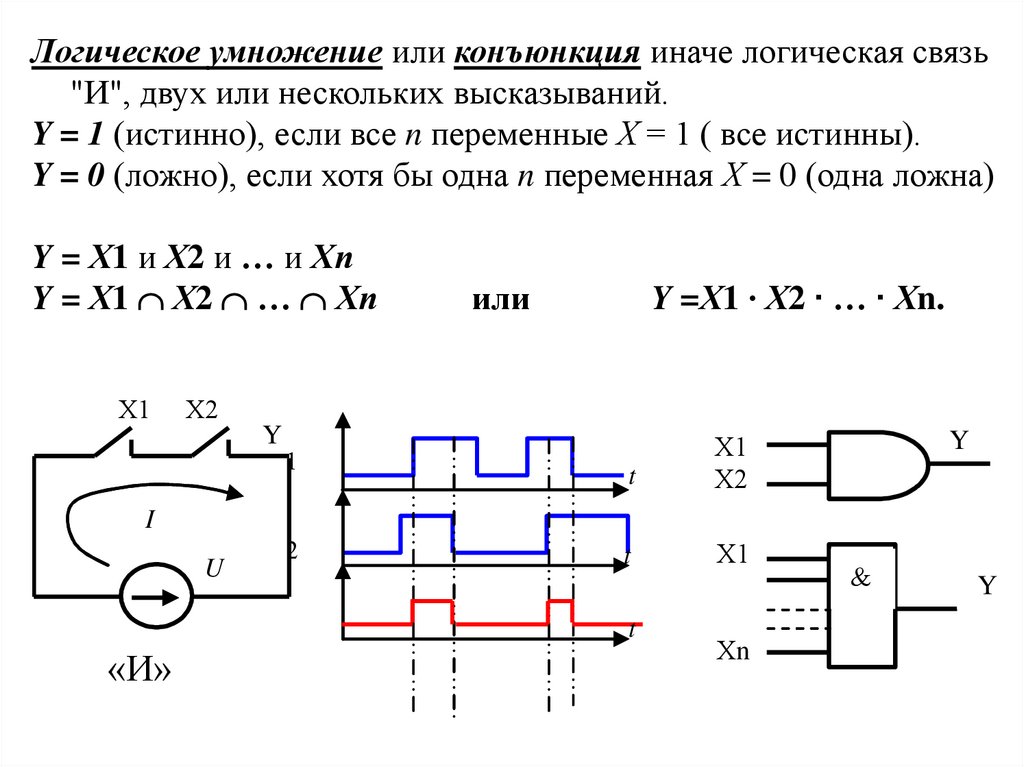
Логическое умножение или конъюнкция иначе логическая связь"И", двух или нескольких высказываний.
Y = 1 (истинно), если все n переменные Х = 1 ( все истинны).
Y = 0 (ложно), если хотя бы одна n переменная Х = 0 (одна ложна)
Y = Х1 и Х2 и … и Хn
Y = Х1 Х2 … Хn
Х1
Y =Х1 ∙ Х2 ∙ … ∙ Хn.
или
Х2
Y
Х1
t
Х1
Х2
t
Х1
Y
I
U
Х2
Y
«И»
t
Хn
Y
4.
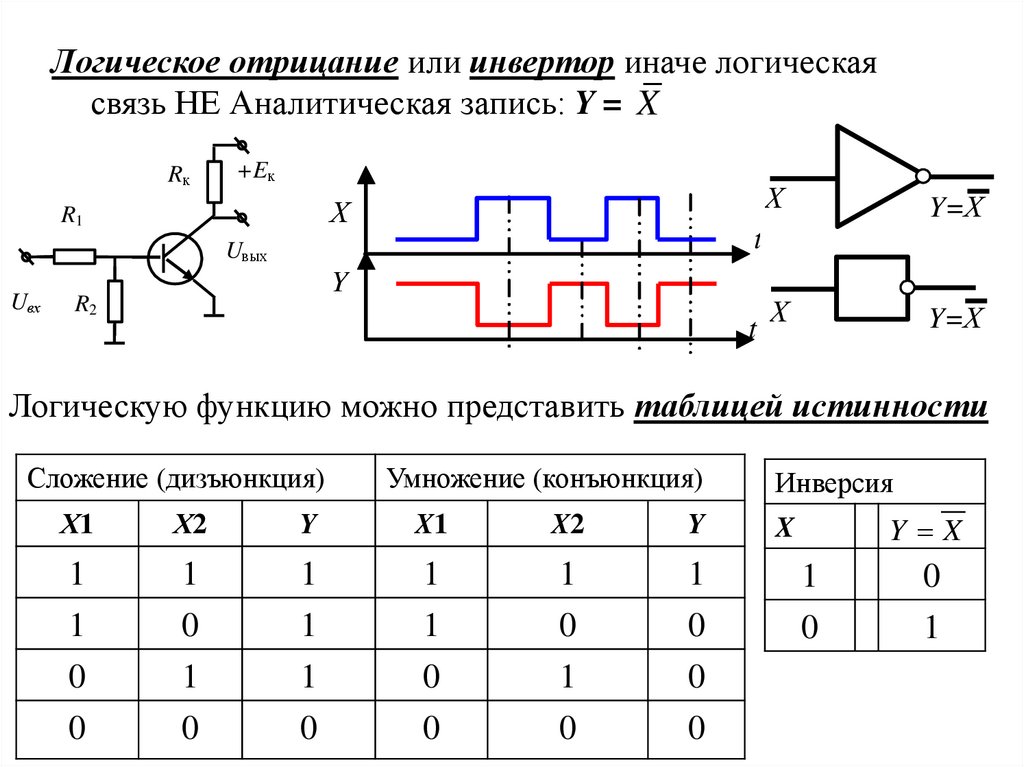
Логическое отрицание или инвертор иначе логическаясвязь НЕ Аналитическая запись: Y = X
Rк
+Eк
Х
R1
Y
R2
Y=Х
Х
Y=Х
t
Uвых
Uвх
Х
t
Логическую функцию можно представить таблицей истинности
Сложение (дизъюнкция)
Умножение (конъюнкция)
Х1
Х2
Y
X1
X2
Y
1
1
1
0
1
1
1
1
1
0
1
0
0
0
1
0
1
0
0
0
1
0
0
0
Инверсия
Y X
X
1
0
0
1
5.
Свойства переключательных функций.Функции вида Y=f(x1, x2,…xn) называется переключательной
функцией ПФ.
ПФ могут быть представлена: аналитически (формулой),
таблицей истинности, принципиальной логической схемой.
Дополнение.
Если q переменная, то ее дополнением будет переменная q
Если Y= (q+p+R ) функция, то ее дополнением будет функция
Y q p R
6.
Основные законы алгебры логики (АЛ).В АЛ есть 4 основных закона, которые устанавливают
эквивалентность логических функций и образованных логических
связей с помощью простых логических функций И, ИЛИ НЕ.
Закон
Для логического
сложения
Для логического
умножения
Переместительный
p+q=q+p
p×q = q×p
(коммутативный)
Сочетательный
(p+q)+R = p+(q+R) (p×q) ×R = p× (q× R)
(ассоциативный)
Распределительный (p+q)×R= p×R+q×R q×p+R = (p+R) ×(q+R)
(дистрибутивный)
Закон инверсии или
Моргана
q p q p
q p q p
7.
Закон Моргана представленный логическими схемамиq
q
1
q+p
q+p
q
qp
1
q+p
=
p
p
p
Для логического сложения
q
qp
q
qp
q
=
p
Для логического умножения
p
p
8.
Аксиомы для одной логической переменной.Всегда справедливо для логического:
сложения
умножения
p+1=1
p × 0 = 0;
p +p = 1
p× p =0
p= p + 0;
p=p×1
p= p + p + p…
p= p × p × p…
p= p
Теоремы склеивания для 2-х переменных:
p × q + p × q=q;
(p + q) × ( p + q)=q;
Доказательство для первой и второй
теоремы:
если р=1, то результат зависит от q,
если р=0, то результат зависит от q
9.
Теоремы поглощения для-2х переменных:p + р × q = p;
p(р +q) = p;
Доказательство для первой и второй
теоремы:
если , p=1 то результат не зависит от q,
если р=0, то результат не зависит от q
p + p q = p + q;
=1
=1
p (q q ) pq pq pq pq pq p (q q ) q ( p p ) p q
Для трех и более переменных всегда справедливы высказывания:
(p + q) (p +r ) (q +r) = pq + pr + qr ;
p pq pqr pqrs..... p q r s.....
p( p q)( p q r )( p q r s )..... pqrs.....
10.
Проектирование логических устройствY1
X1
Логическое
устройство
X2
X3
Y2
Y3
Yn
Xn
Логическое устройство задается в виде таблиц истинности
Х1 Х2 Х3
Y1
Y2
Y3
0
0
0
1
0
1
0
0
1
0
0
0
0
1
0
0
0
1
0
1
1
1
1
0
1
0
0
0
0
0
1
0
1
0
1
0
1
1
0
0
1
1
1
1
1
0
1
1
Y1 = f(x1,x2,x3)
Y2 = f(x1,x2,x3)
Y3 = f(x1,x2,x3)
11.
Совершенные нормальные формы представления ЛФЛФ всегда можно представить в виде:
- суммы произведений переменных,
- произведения сумм переменных.
Дизъюнктивная нормальная форма (ДНФ) Y=f (x1,x2,x3).
пример : Y x1 x 2 x3 x1 x 2 x3 x1 x 2 x3
Конъюнктивная нормальная форма (КНФ).
пример : Y ( x1 x 2 x3) ( x3 x1) x 2 ( x3 x1 x 2)
Для каждой ЛФ может существовать несколько ДНФ и КНФ
Существует только один вид ДНФ и КНФ, в котором функция
может быть записана единственным образом - совершенные
нормальные формы СДНФ и СКНФ.
СНФ содержит все переменные (с инверсиями и без них) и нет
одинаковых слагаемых для СНДФ и одинаковых произведений
для СНКФ
12.
СНДФ и СНКФ записи ЛФ формируются из таблиц истинности.СНДФ
Х1
Х2
Х3
У
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
x1 x 2 x3 1,
1
1
0
1
1
1
1
1
x1 x 2 x3 1,
x1 x2 x3 1.
x1 x 2 x3 1,
Комбинации переменных для которых У=1 называются
конституентами единицы или минтермами.
Сумма минтерм и определяет ее СНДФ:
Y x1 x 2 x3 x1 x 2 x3 x1 x 2 x3 x1 x 2 x3.
13.
СНКФ.Х1
Х2
Х3
У
0
0
0
0
x1 x 2 x3 0,
0
0
1
0
x1 x 2 x3 0,
0
1
0
0
0
1
1
1
x1 x 2 x3 0,
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
x1 x 2 x3 0.
Эти суммы называются
конституентами нуля или
макстермами.
Произведение макстерм определяет СНКФ.
Y ( x1 x2 x3) ( x1 x2 x3) ( x1 x2 x3) ( x1 x2 x3).
14.
СНДФY x1 x 2 x3 x1 x 2 x3 x1 x 2 x3 x1 x 2 x3.
Y x1 x 2 x3 x1 x2 x3 x1 x 2 x3 x1 x 2 x3 x1 x 2 x3 x1 x 2 x3
Y x 2 x3 x1 x3 x1 x 2
СНКФ
Y ( x1 x 2 x3) ( x1 x 2 x3) ( x1 x 2 x3) ( x1 x 2 x3).
Y ( x1 x 2 x3) ( x1 x 2 x3) ( x1 x 2 x3) ( x1 x 2 x3)
( x1 x 2 x3) ( x1 x 2 x3). По теореме склеивания ( p q)( p q) p
Y ( x1 x 2) ( x1 x3) ( x 2 x3).
И по теореме склеивания для 3-х переменных: (p + q) (p +r ) (q +r) = pq + pr + qr
Y x1 x 2 x1 x3 x 2 x3
15.
F x1 x 2 x1 x 2 ( x1 x1) x 2 x 2F x1 x1 x 2 x3 x1 x3
F x1 ( x1 x 2 ) x 2 ( x 2 x3 ) x3 x1 x 2 x3
F x1 x 2 x1 x3 x 2 x 4 x1 x 2 x 2 x 4
x1 x 2 x 4
F x1 x 2 x1 x 2 x3 x1 x 2 x1 x 2 x3 x1 x 2 x3 x1x 2 x3
16.
Примеры преобразования заданных ЛФ к более простым выражениямиспользуя законы и аксиомы АЛ.
F x1 x 2 x1 x 2 x 2 ( x1 x1) x 2
F x1 x1 x 2 x3 x1 (1 x 2) x3 x1 x3
F x1 ( x1 x 2 ) x 2 ( x 2 x3 ) x3
x1 x1 x1 x 2 x 2 x 2 x 2 x3 x3
x1 x 2 x3 ( x 2 1) x1 x 2 x3
F x1 x 2 x1 x3 x 2 x 4 x1 x 2 x1 x3 x 2 x 4
x1 (1 x3) ( x 2 x 2 x 4) x1 x 2 x 4
Закон Моргана
Теорема поглощения
F x1 x2 x1 x2 x3 x1 x2 x1 x2 x3 x1 x2 x3 x1x2x3
Закон Моргана
17.
Карты «Карно»При большем числе переменных используют специальные методы
преобразования. К таким методам относятся карты Карно.
КК для 2-х переменных
X1
X2
X2
X1
X1 X2
X 1 X2
X1 X 2
X1 X 2
X1
X1
X2
Y
0
0
0
0
1
1
1
0
1
1
1
0
X1
X2
0
1
X2
1
0
Карту Карно заполняют
минтермами
18.
Для 3-х переменныхX1
X1
X1
X1
X2
X1 X2 X3
X1 X2 X 3
X 1 X2 X 3
X 1 X2X3
X2
X1 X 2 X3
X1 X 2 X 3
X1 X 2 X 3
X 1 X 2 X3
X3
X3
X3
X3
Правило для составления КК.
Соседние ячейки могут отличаться только на один
элемент, который является его дополнением.
19.
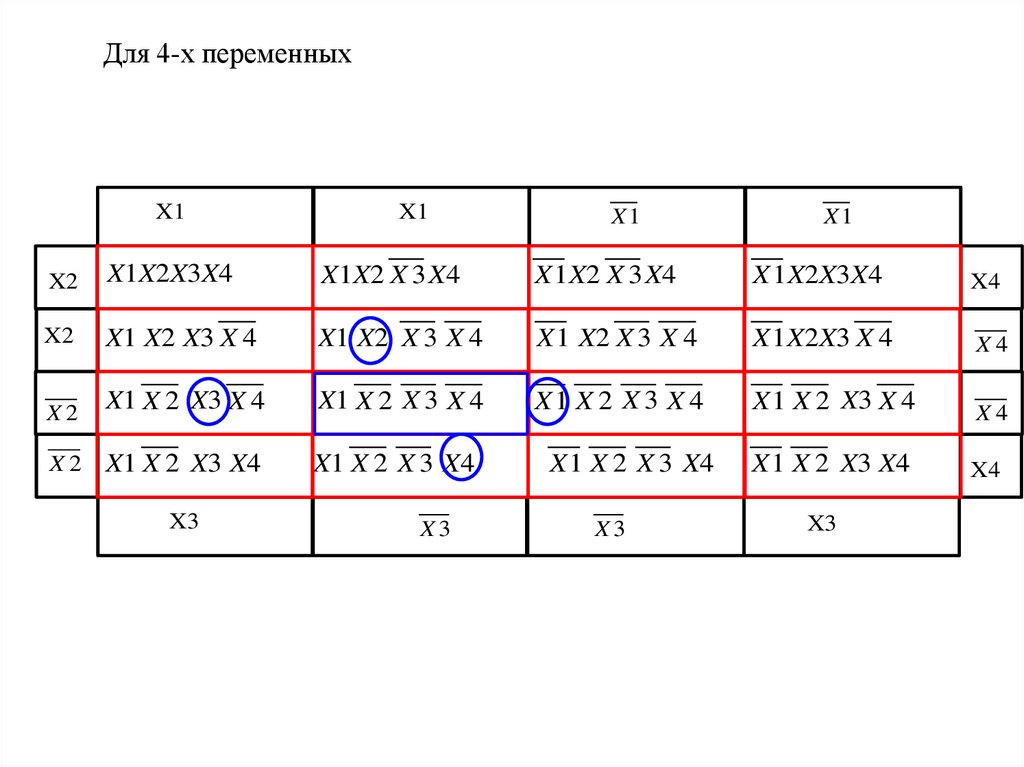
Для 4-х переменныхX1
X1
X1
X1
X2
X1X2X3X4
X1X2 X 3 X4
X 1 X2 X 3 X4
X 1 X2X3X4
X4
X2
X1 X2 X3 X 4
X1 X2 X 3 X 4
X 1 X2 X 3 X 4
X 1 X2X3 X 4
X4
X2
X1 X 2 X3 X 4
X1 X 2 X 3 X 4
X1 X 2 X 3 X 4
X 1 X 2 X3 X 4
X4
X2
X1 X 2 X3 X4
X1 X 2 X 3 X4
X 1 X 2 X3 X4
X4
X3
X3
X 1 X 2 X 3 X4
X3
X3
20.
Соседними называют клетки - справа, слева, сверху, снизу.Если минтермы расположены в соседних клетках, то говорят,
что они «склеиваются».
Правила группирования:
• Карта Карно не имеет границ. Крайние верхние и нижние,
правые и левые - соседние.
• Группирование (объединение) производят по 2, 4, 8 и более
соседних клеток.
• Сколько объединений (групп) столько и слагаемых будет в
упрощенной форме функции.
• Одна клетка может входить в несколько групп.
• Каждое слагаемое упрощенной функции включает только
произведения переменных, которые входят во все клетки
объединения.
21.
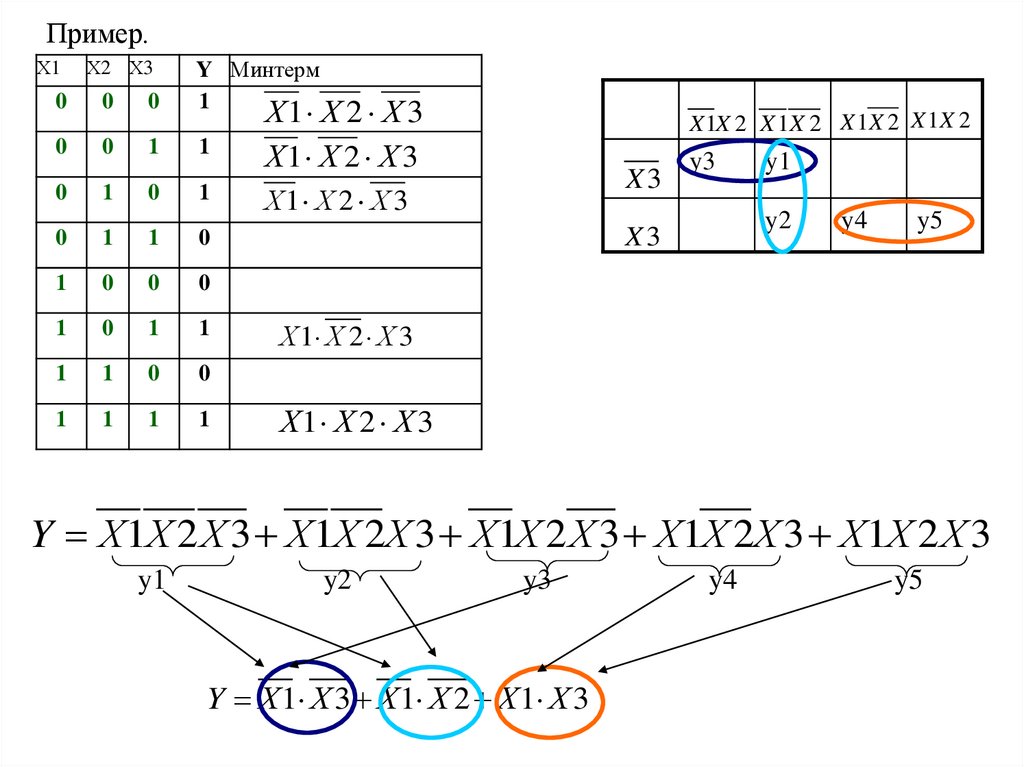
Пример.Х1
Х2 Х3
0
0
0
Y Минтерм
1
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
1
Х1 Х 2 Х 3
Х1 Х 2 Х 3
X 1X 2 X 1X 2 X 1X 2 X 1X 2
X3
Х1 Х 2 Х 3
y3
y1
y2
X3
y4
y5
Х 1 Х 2 Х 3
Х1 Х 2 Х 3
Y Х1X 2 Х 3 Х1Х 2X 3 X1X 2 X 3 Х1X 2Х 3 X1X 2 X 3
y1
y2
y3
Y Х 1 Х 3 Х 1 Х 2 Х 1 Х 3
y4
y5
22.
Такой же результат получается, если воспользоваться логическимипреобразованиями с помощью аксиом и законов АЛ.
Y Х1X 2 Х 3 Х1Х 2X 3 Х1X 2Х 3 X1X 2 X 3 X1X 2 X 3
Y Х1X 2 Х 3 Х 1Х 2X 3 Х 1X 2Х 3 X 1X 2 X 3 X1X 2 X 3 X 1X 2 X 3
=1
=1
Y Х 1X 2( Х 3 X 3) X 1X 3( X 2 X 2) X 1X 3( X 2 X 2)
Y Х1X 2 X 1X 3 X 1X 3
=1
23.
Х1Х2 Х3
0
0
0
Y Минтерм
1
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
1
Х1 Х 2 Х 3
Х1 Х 2 Х 3
X 1X 2 X 1X 2 X 1X 2 X 1X 2
X3
Х1 Х 2 Х 3
y3
y1
y2
X3
Х 1 Х 2 Х 3
Х1 Х 2 Х 3
Y Х1X 2 Х 3 Х1Х 2X 3 X1X 2 X 3 Х1X 2Х 3 X1X 2 X 3
y1
y2
y3
y4
Y Х 1 Х 3 Х 1 Х 2 Х 1 Х 3
y5
y4
y5
24.
Х10
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Х2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
Х3
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
Х4
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
0
0
1
1
0
0
1
1
0
0
1
1
1
0
1
X2
X1
X1
1
1
X2
1
1
X2
X2
X1
1
X4
1
X4
1
X4
1
X3
X1
1
X3
X3
X4
X3
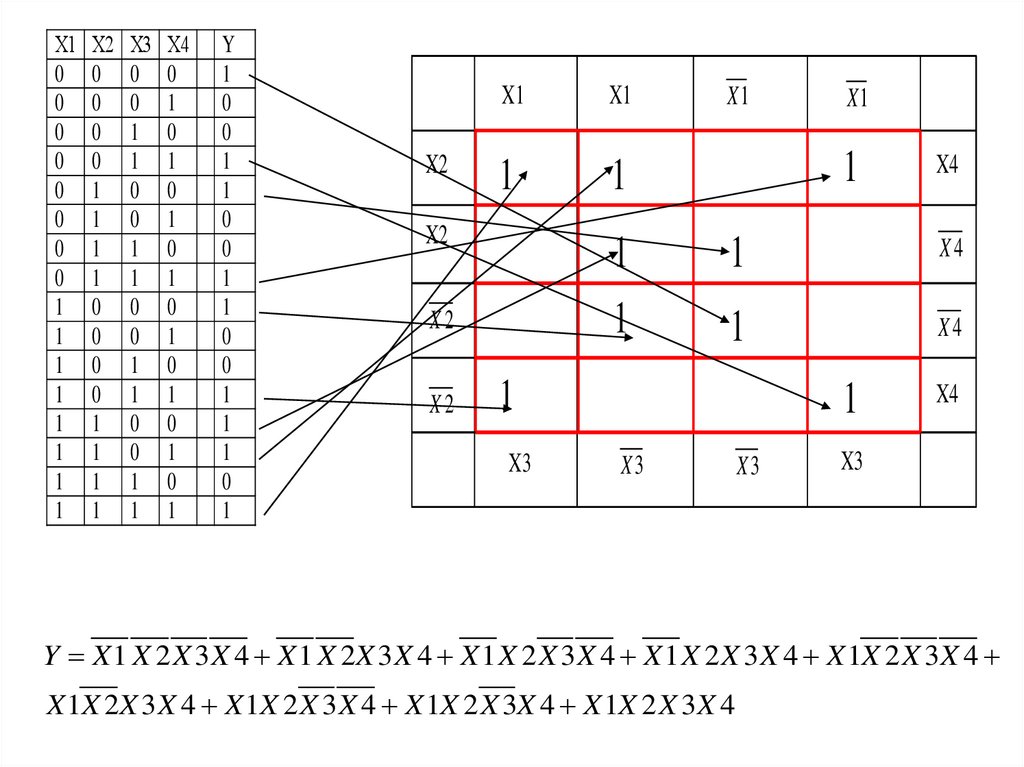
Y X 1 X 2 X 3 X 4 X 1 X 2X 3 X 4 X 1 X 2 X 3 X 4 X 1 X 2 X 3 X 4 X 1X 2 X 3 X 4
X 1X 2X 3 X 4 X 1X 2 X 3 X 4 X 1X 2 X 3X 4 X 1X 2 X 3 X 4
25.
Х10
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Х2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
Х3
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
Х4
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
0
0
1
1
0
0
1
1
0
0
1
1
1
0
1
X2
X1
X1
1
1
X2
1
1
X2
X2
X1
1
X4
1
X4
1
X4
1
X3
X1
1
X3
X3
X4
X3
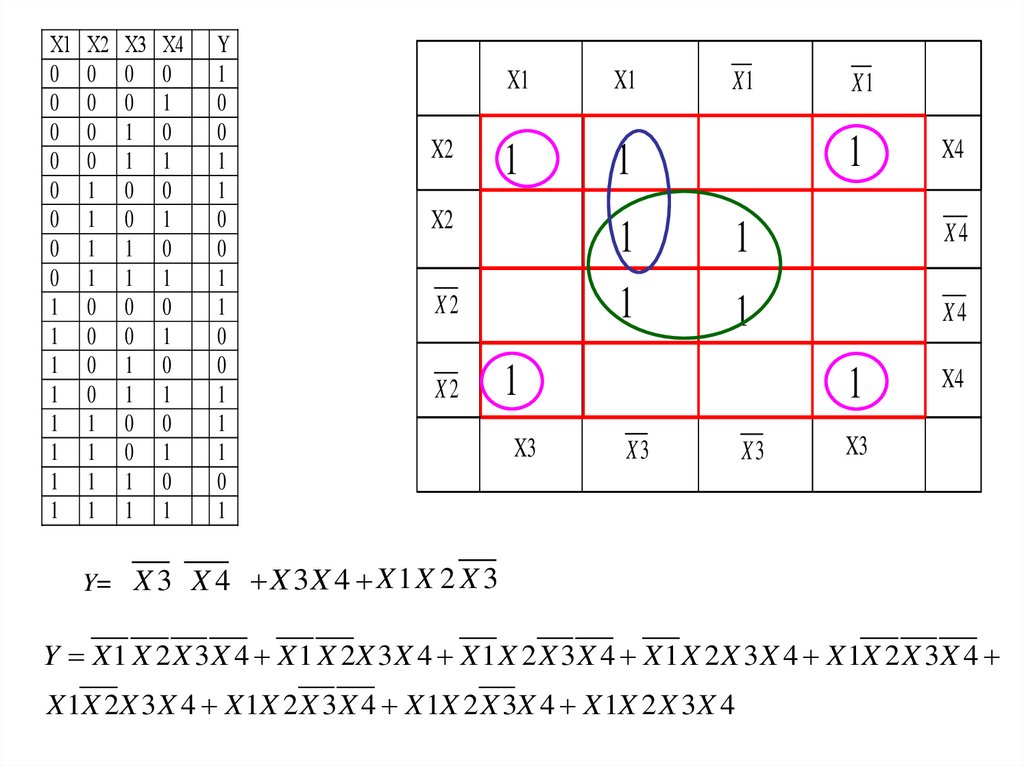
Y= X 3 X 4 X 3 X 4 X 1 X 2 X 3
Y X 1 X 2 X 3 X 4 X 1 X 2X 3 X 4 X 1 X 2 X 3 X 4 X 1 X 2 X 3 X 4 X 1X 2 X 3 X 4
X 1X 2X 3 X 4 X 1X 2 X 3 X 4 X 1X 2 X 3X 4 X 1X 2 X 3 X 4
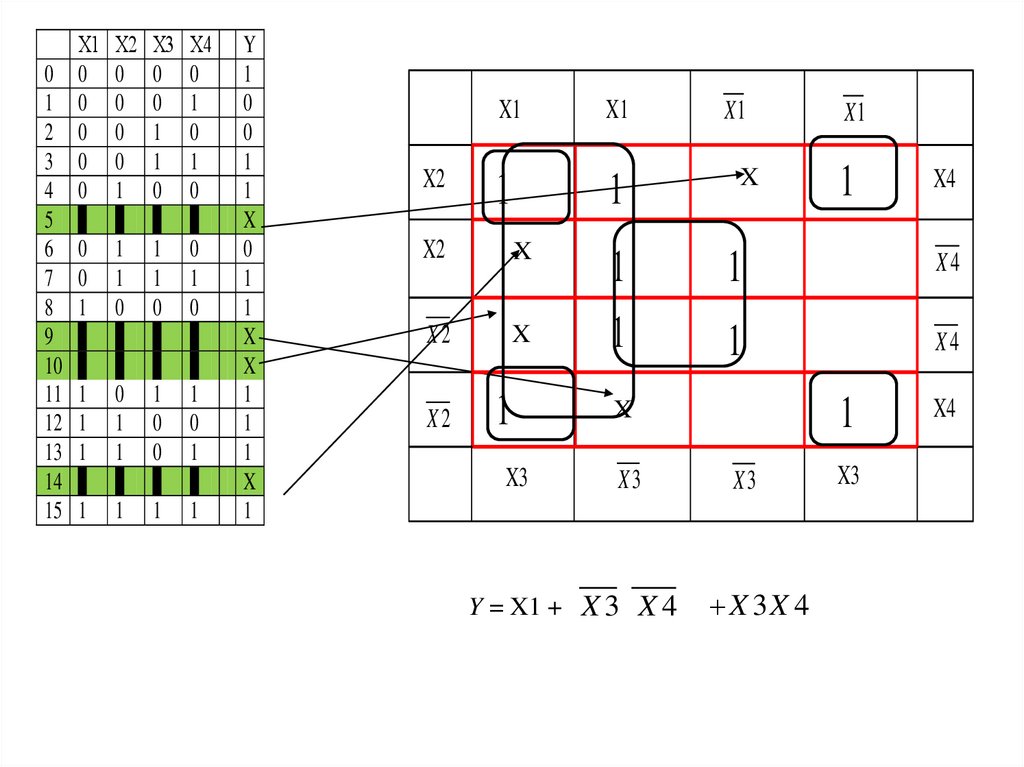
26.
01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Х1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Х2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
Х3
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
Х4
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
0
0
1
1
X
0
1
1
X
X
1
1
1
X
1
X2
X1
X1
1
1
X2
X
X2
X
X2
1
X3
1
1
X1
X
Y = X1 + X 3 X 4
1
X4
1
X4
1
X4
1
X
X3
X1
X3
X 3X 4
X3
X4
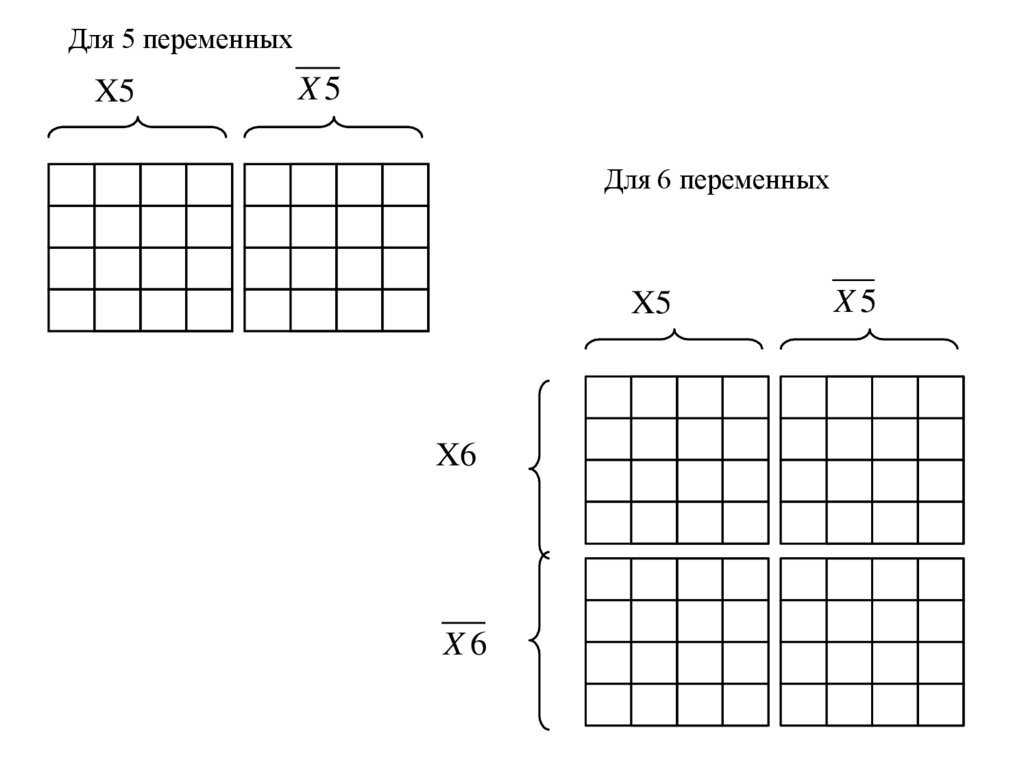
27.
Для 5 переменныхX5
X5
Для 6 переменных
X5
X6
X6
X5
28.
Функциональные логические схемыЛФ (переключательную) можно составить из И, ИЛИ, НЕ
Пример. Рассмотрим ЛФ «исключающая ИЛИ» (операция
сложения по модулю два, неравнозначность).
X1
X2
Y
0
0
0
1
0
1
0
1
1
1
1
0
Y x1 x2 x1 x2 x1 x2 x1 x1 x2 x2
x1 ( x2 x1 ) x2 ( x2 x1 )
Y x1 x 2 x1 x 2 x1 x 2
Y x1 x2 ( x1 x2 ) x1 x2
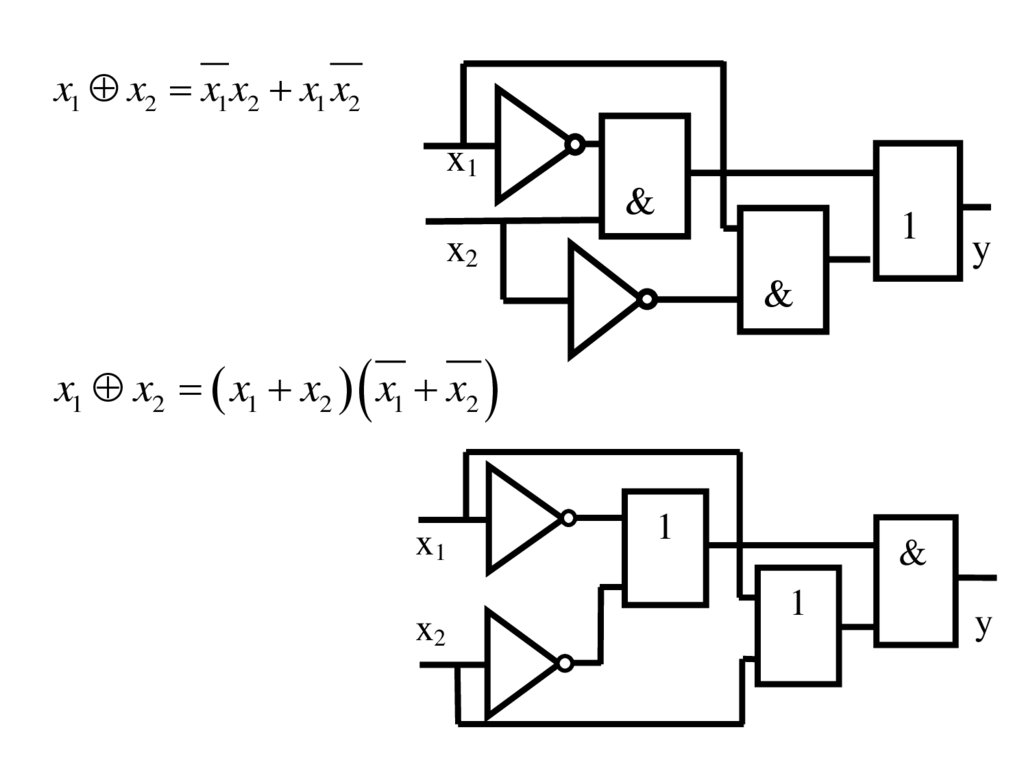
29.
x1 x2 x1 x2 x1 x2x1
1
x2
x1 x2 x1 x2 x1 x2
x1
x2
y
1
&
1
y
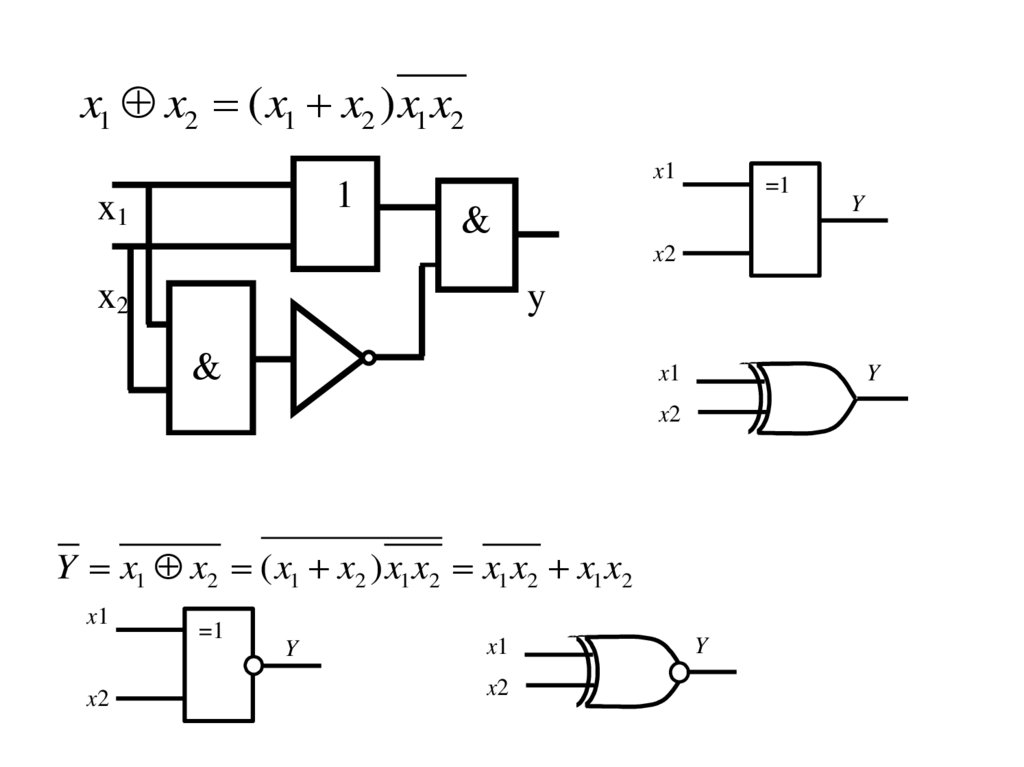
30.
x1 x2 ( x1 x2 ) x1 x21
x1
x1
=1
Y
x2
x2
y
Y
x1
x2
Y x1 x2 ( x1 x2 ) x1 x2 x1 x2 x1 x2
x1
x2
=1
Y
x1
x2
Y
31.
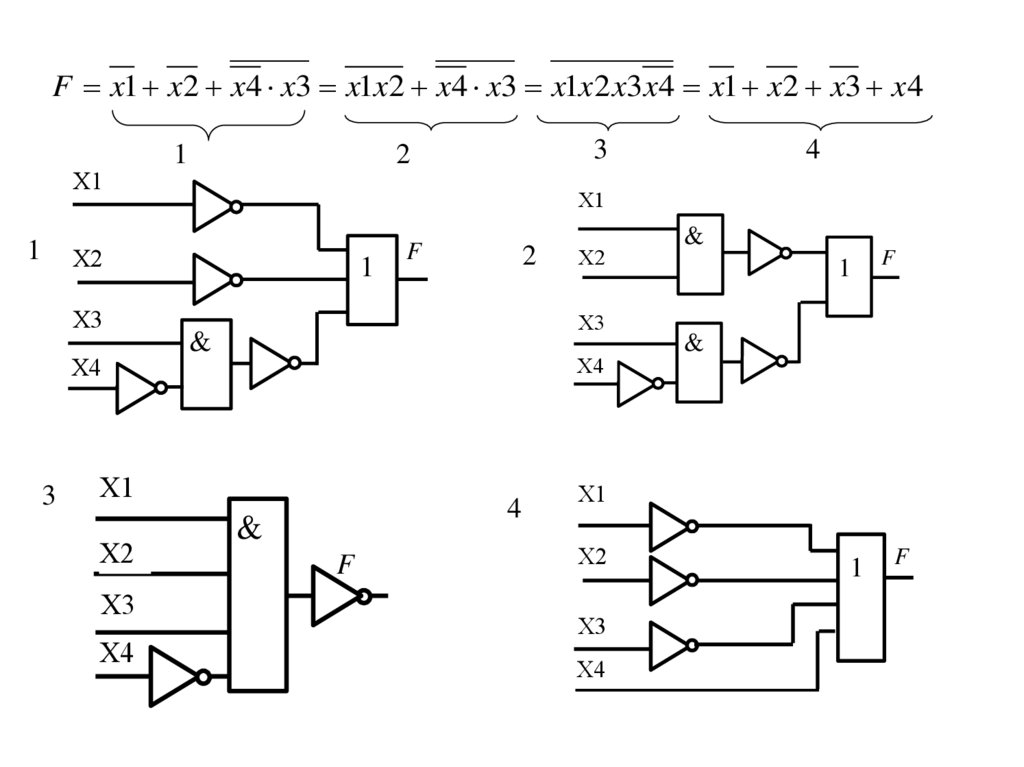
F x1 x 2 x 4 x3 x1x 2 x 4 x3 x1x 2 x3x 4 x1 x 2 x3 x 4Х1
1
1
Х4
3
1
Х3
Х4
F
2
Х2
Х3
&
Х4
Х1
Х2
4
Х1
Х2
Х3
3
2
4
&
F
&
1
F
&
Х1
Х2
Х3
Х4
1
F
32.
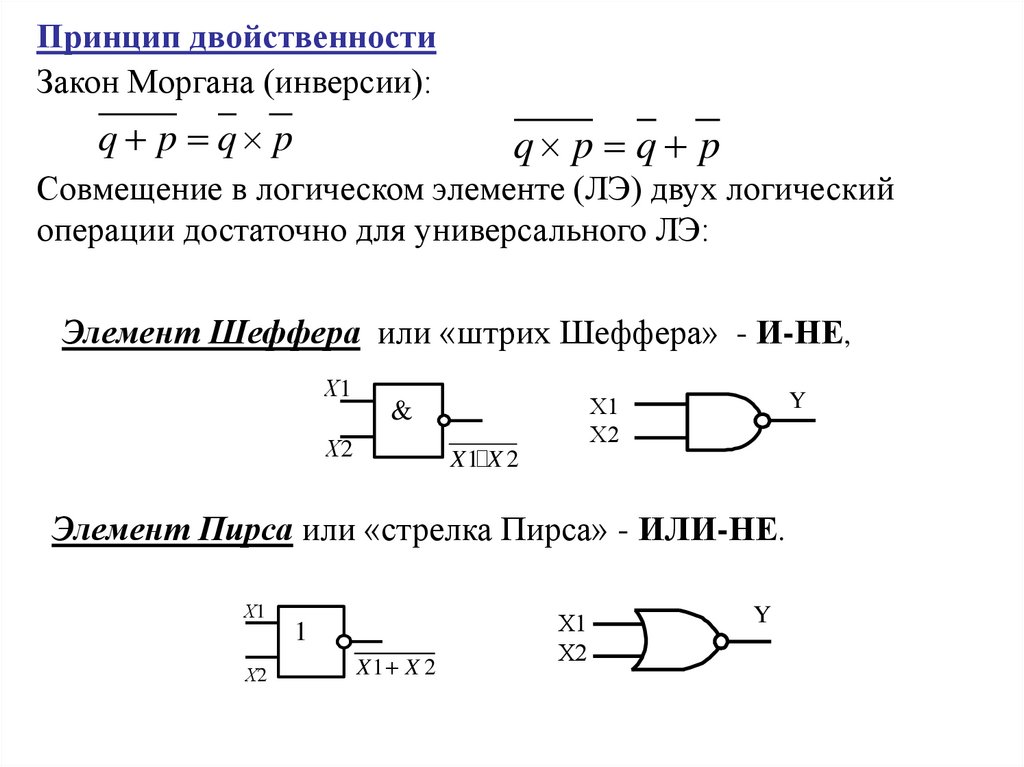
Принцип двойственностиЗакон Моргана (инверсии):
q p q p
q p q p
Совмещение в логическом элементе (ЛЭ) двух логический
операции достаточно для универсального ЛЭ:
Элемент Шеффера или «штрих Шеффера» - И-НЕ,
Х1
Х2
Y
Х1
Х2
&
X1 X 2
Элемент Пирса или «стрелка Пирса» - ИЛИ-НЕ.
Х1
1
Х2
X1 X 2
Х1
Х2
Y
33.
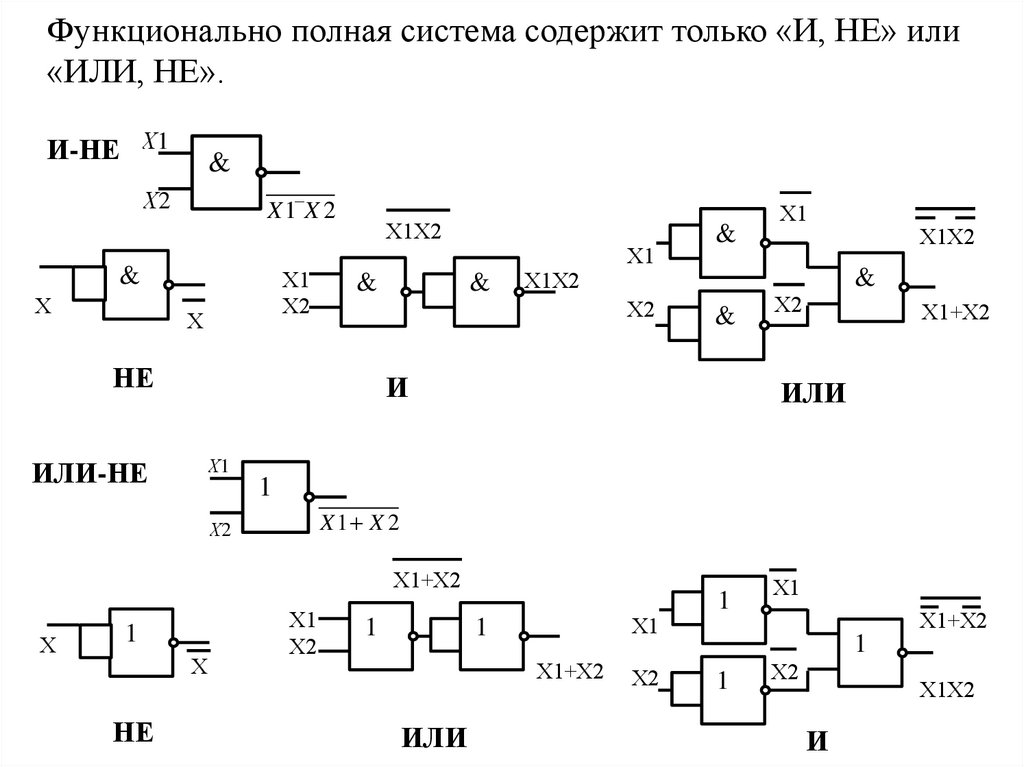
Функционально полная система содержит только «И, НЕ» или«ИЛИ, НЕ».
И-НЕ Х1
&
Х2
X1 X 2
&
Х
Х1
Х2
Х
Х1Х2
&
НЕ
&
Х1Х2
Х1
Х2
Х1
Х1Х2
&
Х2
Х1+Х2
ИЛИ
Х1
1
X1 X 2
Х2
Х1+Х2
1
Х
НЕ
&
И
ИЛИ-НЕ
Х
&
Х1
Х2
1
Х1
1
Х1+Х2
ИЛИ
Х2
1
Х1
Х1+Х2
1
1
Х2
Х1Х2
И
34.
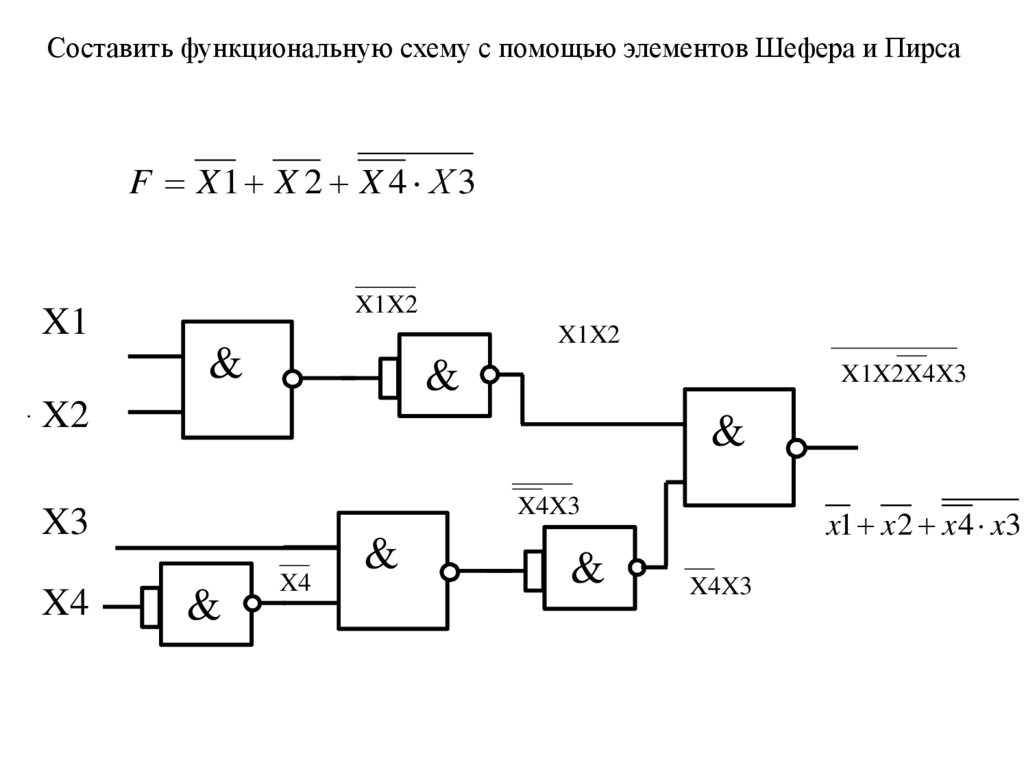
Составить функциональную схему с помощью элементов Шефера и ПирсаF X1 X 2 X 4 Х 3
X1X2
X1
X1X2
&
.
&
X1X2X4X3
X2
&
X4X3
X3
X4
&
X4
&
&
x1 x 2 x 4 x3
X4X3
35.
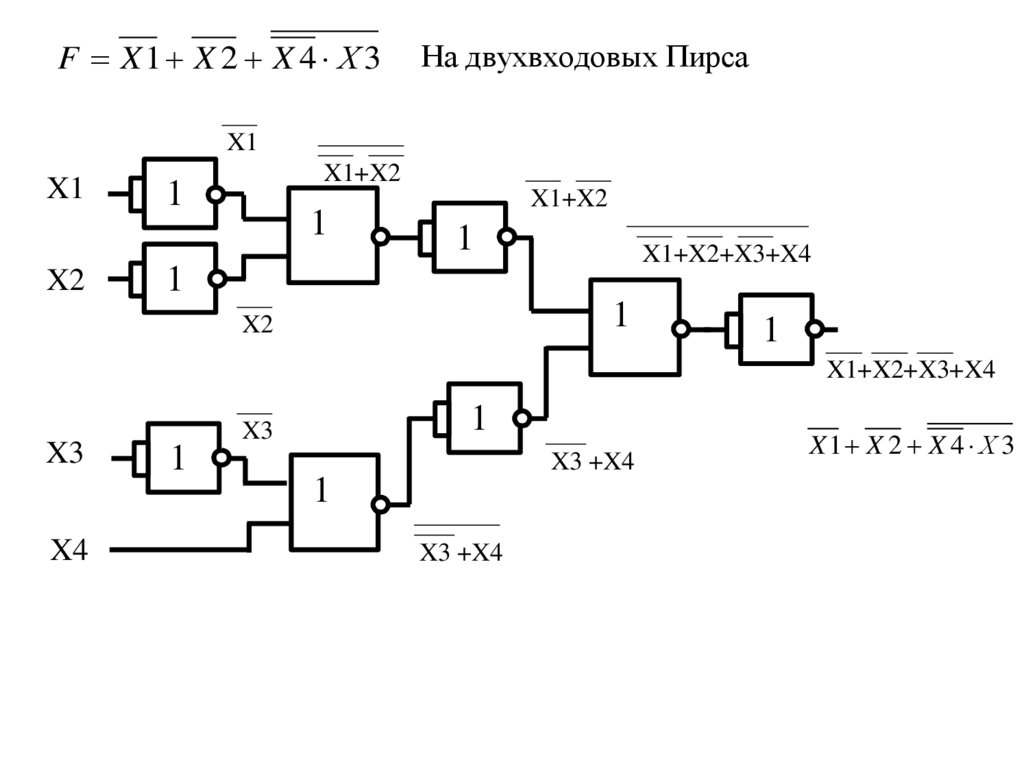
F X1 X 2 X 4 Х 3На двухвходовых Пирса
X1
X1
X2
X1+X2
1
1
X1+X2
1
X1+X2+X3+X4
1
1
X2
1
X1+X2+X3+X4
X3
X4
1
X3
1
X3 +X4
1
X3 +X4
X1 X 2 X 4 Х 3











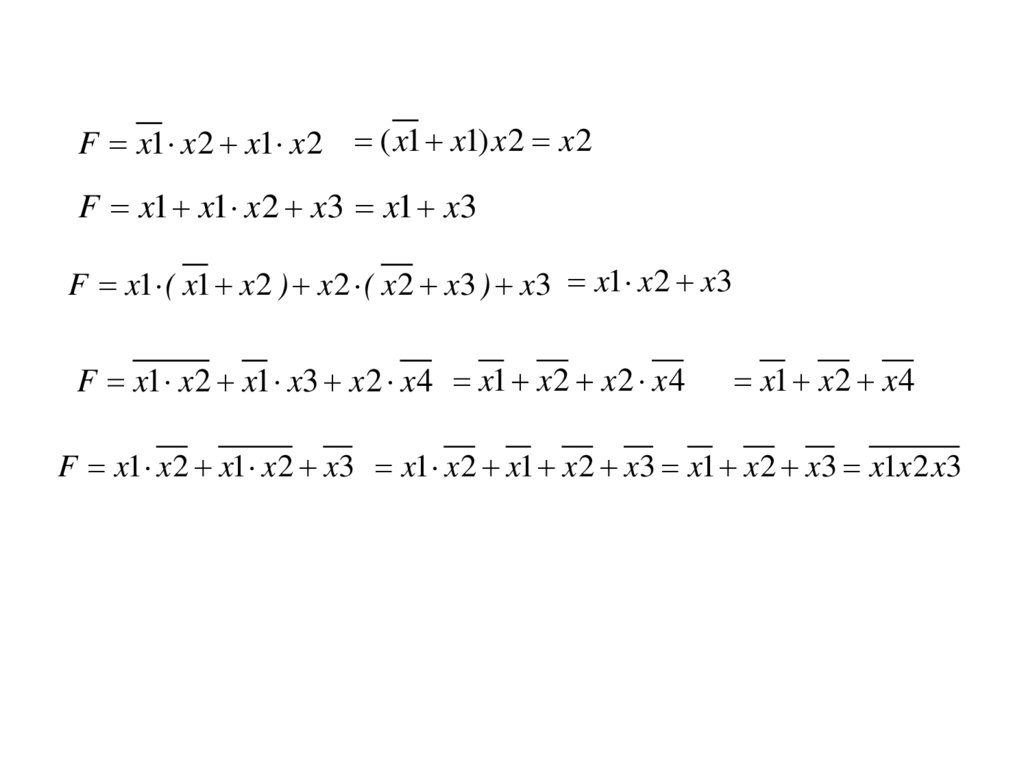







 mathematics
mathematics








