История математических символов

1.

ГБОУ СОШ № 183 с углубленным изучением английского языка
Центрального района Санкт — Петербурга
Ежегодная научно-практическая конференция
VII ученические чтения
2014г
Проектная работа учащихся 5б класса
«История
математических символов»
Работу выполнили: Быданцев Георгий, Говзич Ярослав,
Григорьев Сергей, Ельшова Валерия, Моденова Арина, Лужина
Анна, Лукина Ксения, Оршанская Мирра
Руководитель: учитель математики Шарко Т В

2. «Все располагается согласно числам» Пифагор

Проект направлен на развитие представления о числе,
изучения истории возникновения чисел и влияния, которое
они оказали на развитие человеческой цивилизации.
Цель проекта:
изучение знаковой системы обозначения чисел, истории
их возникновения, эволюционных изменениях,
происходивших с цифрами с течением времени.
Задачи:
изучить и описать различные системы счисления
древности;
сравнить позиционные и непозиционные системы
счисления, выделить наиболее удобные;
оформить в виде презентации свои исследования.

3.

Китайская
нумерация

4.

Возникла эта нумерация
около 4 000 тысяч лет
тому назад в Китае.

5.

Обычная запись:
十
10

6.

Формальная запись:
壹
1
貳,
2
叁
3
肆
4
伍
5
陸
6
柒
7
捌
8
玖
9
拾
10

7.

Чтобы записать число нужно
цифру умножить на идущую
за ней степень десятки.
Например, число 600
записывается как 6 х 100
六百

8. История математических символов. Индийская нумерация.

9. Индийская поместная нумерация.

• В различных областях Индии
существовали разнообразные системы
нумерации. Одна из них
распространилась по всему миру и в
настоящее время является
общепринятой. В ней цифры имели вид
начальных букв соответствующих
числительных на древнеиндийском
языке – санскрите.

10.

• Первоначально этими знаками
представлялись числа 1, 2, 3, … , 9, 10,
20, 30, … , 90, 100, 1000; с их помощью
записывались другие числа.
Впоследствии был введен особый знак
(жирная точка или кружок) для указания
пустующего разряда; знаки для чисел,
больших 9, вышли из употребления, и
нумерация «деванагари» превратилась в
десятичную поместную систему.

11.

• Решающую роль в распространении
индийской нумерации в арабских странах
сыграло руководство, составленное в начале
IX века узбекским ученым Мухаммедом из
Хорезма . Оно было переведено в Западной
Европе на латинский язык в XII веке.
• В XIII веке индийская нумерация получает
преобладание в Италии.
• В других странах Западной Европы она
утверждается в XVI веке. Европейцы,
заимствовавшие индийскую нумерацию от
арабов, называли ее «арабской». Это
исторически неправильное название
удерживается и поныне.

12. «цифра» (по-арабски «сыфр»).

• Нуль:
• Один:
• Два:
• Четыре:

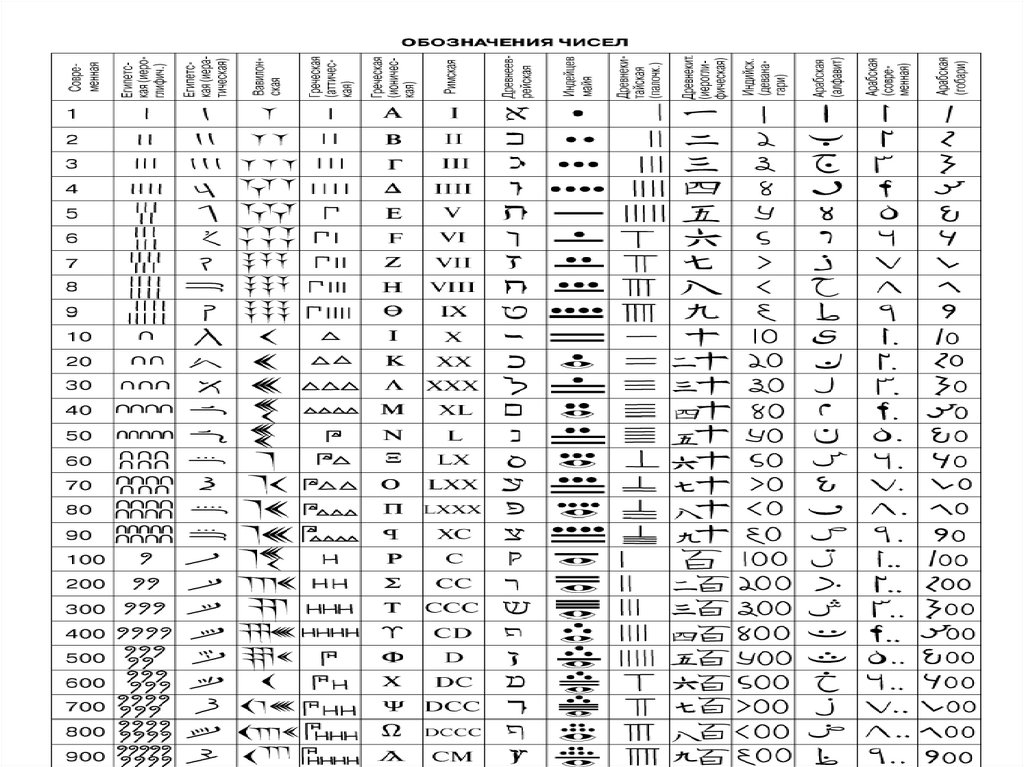
13. Эволюция арабских цифр

Индийская нумерация распространилась по всему миру. При этом одни
народы переняли у индийцев только принцип обозначения чисел, другие
заимствовали и написание цифр. На приведенной таблице видно, как
постепенно видоизменялись цифры , употреблявшиеся в мавританских
государствах.

14.

НУМЕРАЦИЯ НАРОДОВ
МАЙЯ

15.

В центральной Америке на полуострове Юкотан жил
индейский народ майя, имевший уже в VI-VIII веках н.э.
высокую культуру. Этот народ имел две системы записи
чисел.
Одна система применялась в
повседневной жизни.
Вторая система применялась в
календарных расчетах.

16.

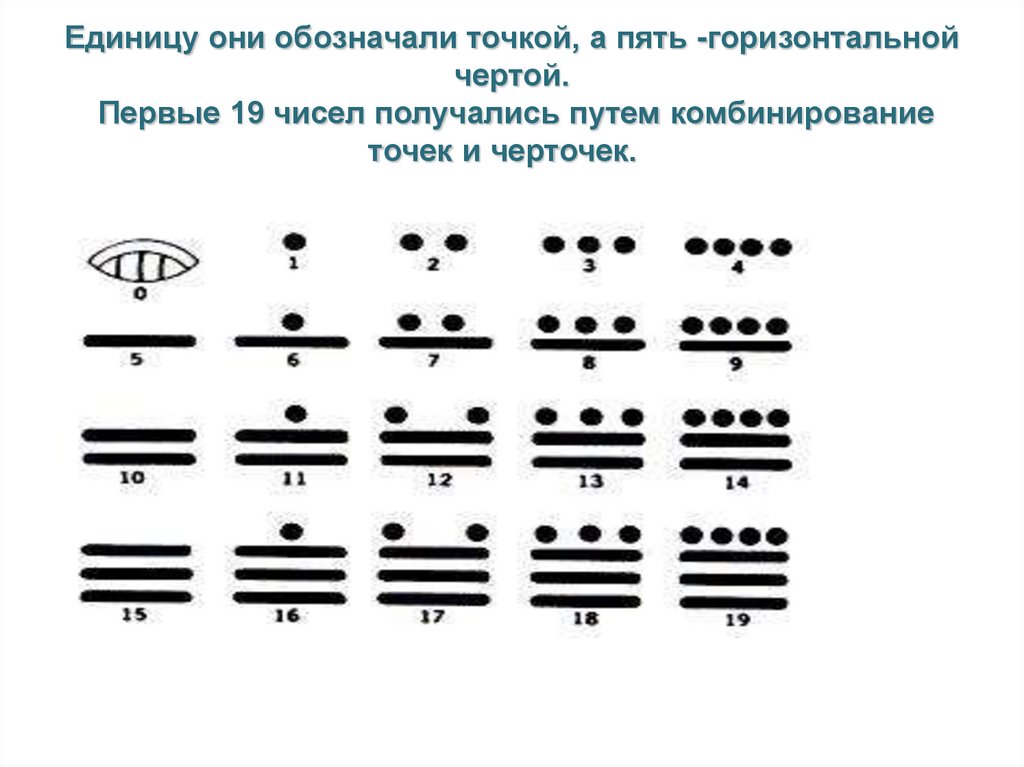
Единицу они обозначали точкой, а пять -горизонтальной
чертой.
Первые 19 чисел получались путем комбинирование
точек и черточек.

17.

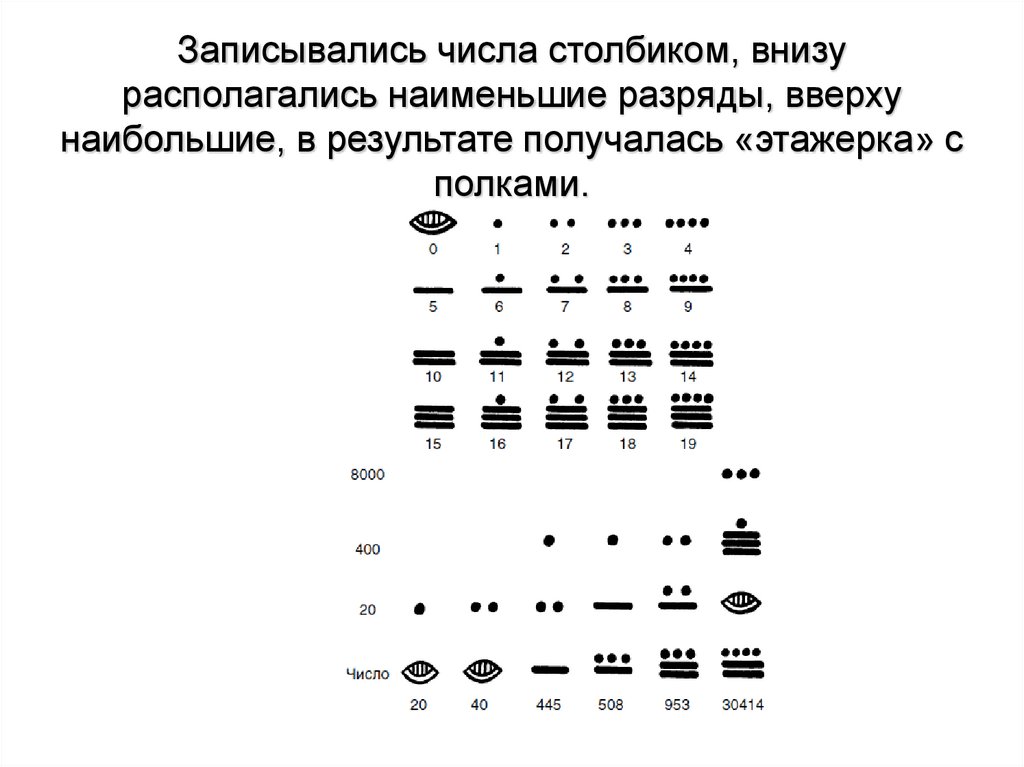
В нумерации майя был знак для нуля. Он
напоминал по своей форме
полузакрытый глаз.
Например, число 20 индейцы майя
записывали при помощи знака для
единицы и внизу знака для нуля. Это
число называлось уиналу.

18.

Записывались числа столбиком, внизу
располагались наименьшие разряды, вверху
наибольшие, в результате получалась «этажерка» с
полками.

19.

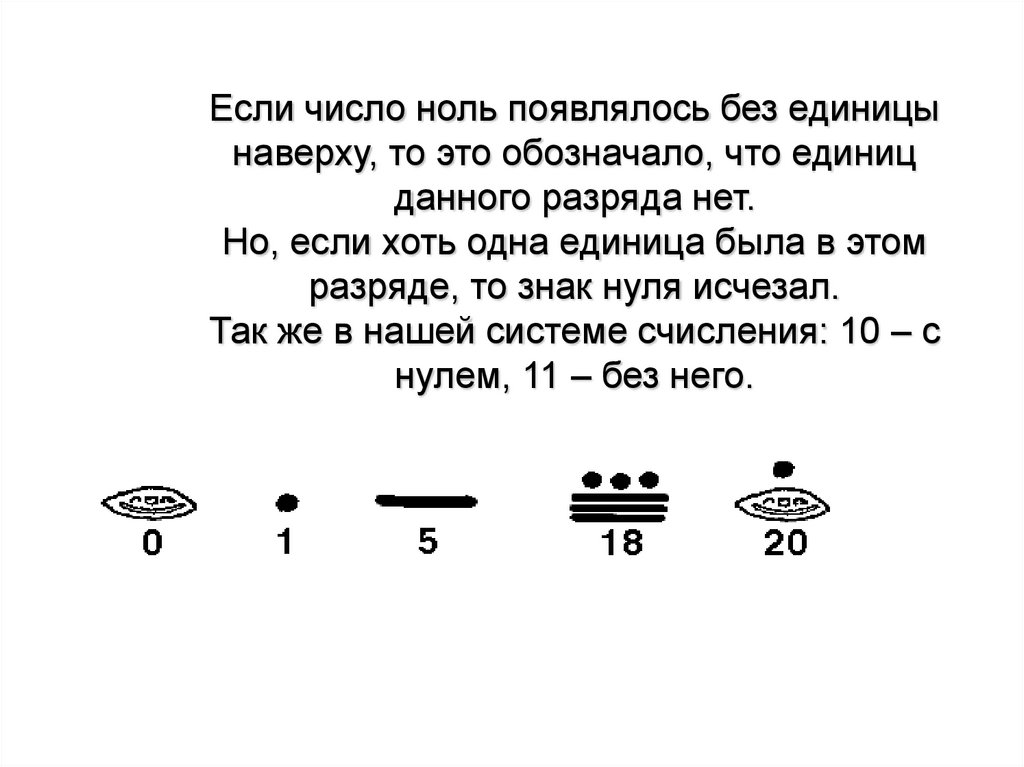
Если число ноль появлялось без единицы
наверху, то это обозначало, что единиц
данного разряда нет.
Но, если хоть одна единица была в этом
разряде, то знак нуля исчезал.
Так же в нашей системе счисления: 10 – с
нулем, 11 – без него.

20. Славянская нумерация

21.

• Славянские цифры обозначались
строчными славянскими буквами

22.

• Над буквами, изображающими числа, ставится
особый значок – титло (м).
• Числа одиннадцать, двенадцать, например,
записывались так: ai. Ei., двадцать один, двадцать
два, и т. д. Титло ставилось только над одной из букв.
• Порядок цифр в числе был такой же, как в его
названии. Мы говорим, например, «пятнадцать» (пославянски – «пятьнадесять»). В старину так и писали:
еi.
• Впереди писали пятёрку, а за нею десяток.
Наоборот, в числе «двадцать три» мы сначала
называем десятки, потом единицы; у наших
предков это отражалось и в письме: они писали кг.
Место цифры, её положение в числе не имело
значения. У нас же теперь одна и та же цифра, в
зависимости от её положения, может обозначать
разные числа. Например, цифра 2 в числах 12, 23,
215 обозначает в первом-два, во втором-двадцать,
в третьем – двести.

23.

• Для обозначения чисел
больших, чем 900
использовались
специальные значки,
которые дорисовывались к
букве. Так образовывались
числа:
• Славянская нумерация
просуществовала до конца
XVII столетия, пока с
реформами Петра I в
Россию из Европы не
пришла позиционная
десятичная
система счисления.
тысяча
1000
тьма
10 000
легион
100 000
леодр
1000 000
ворон
10 000 000
колода
100 000000

24.

25. Заключение

Выполнив данную работу, мы изучили историю
возникновения цифр. Узнали, как выглядели первые
цифры, почему с течением времени они менялись.
Изучили правила римской системы счисления, а так
же ознакомились с системами счисления.
В итоге работы был получен программный продукт,
расширяющий кругозор учащихся. Данный материал
может быть использован в качестве дополнительного
к урокам, а также для проведения внеклассных
мероприятий.
Данное наше небольшое исследование не
исчерпывает всех аспектов истории возникновения
чисел и цифр. Необходимы более глубокие
исследования данной темы, так как с множеством
чисел мы продолжаем знакомство на уроках
математики.

26. Список используемой литературы.

• Акимова С. Занимательная математика. – СПб.; Тригон, 1997.
• Дектярёва З. А. Математика после уроков. - Краснодар, 1996.
• Депман И. Я. За страницами учебника математики. – М.;
Просвещение,1989.
• Депман И Я Рассказы о математике
• «история арифметики», пособие для учителей, М.,
Просвещение, 1965г
• Математика: Школьная энциклопедия. – М.; «Большая
Российская энциклопедия», 1996.
• Позднякова А. Г. Математический вечер в школе. / Математика в
школе. – 1989. - № 5.
• Трифонов Д. Математические силуэты «звериного» числа. /
Математика – 1999. - № 1.
• Шеина О. С., Соловьёва Г. М. Математика. Занятие школьного
кружка. 5 – 6 класс. – М., НЦ ЭНАС, 2001.
• Щербакова Ю. В. Занимательная математика на уроках и
внеклассных мероприятиях. 5 – 8 классы. – М.; ООО «Глобус»,
2008.
• 10. Я познаю мир: Детская энциклопедия: Математика./ Под ред.
О. Г. Хини. – М.; АСТ – ЛТД, 1997.

27. Список используемых источников

Сайты:
1. academic.ru
2. ancients-10.allrpg.info
3.
4.
5.
6.
7.
8.
9.
ido.tsu.ru
http://yunc.org
http://festival.1september.ru
http://ikt-tarantina.ucoz.ru
http://viki.rdf.ru
www.ponimalka.info
www.foundbasis.narod.ru