Similar presentations:
Нули функции
1. Нули функции
ОпределениеНахождение нулей функции, заданной
графически
Нахождение нулей функции, заданной
формулой
2.
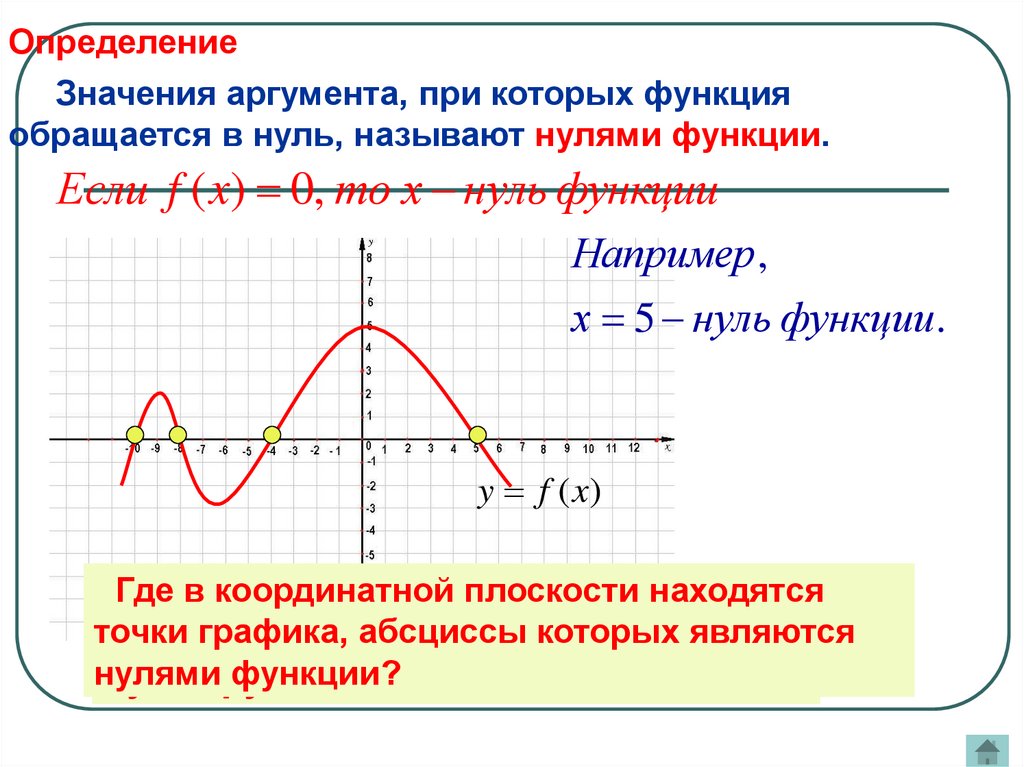
ОпределениеЗначения аргумента, при которых функция
обращается в нуль, называют нулями функции.
Если f ( x) 0, то х нуль функции
Например ,
х 5 нуль функции .
y f (x)
Где в координатной плоскости находятся
По графику
точки
графика,найдите
абсциссыостальные
которых являются
нулями
функции?
нули функции
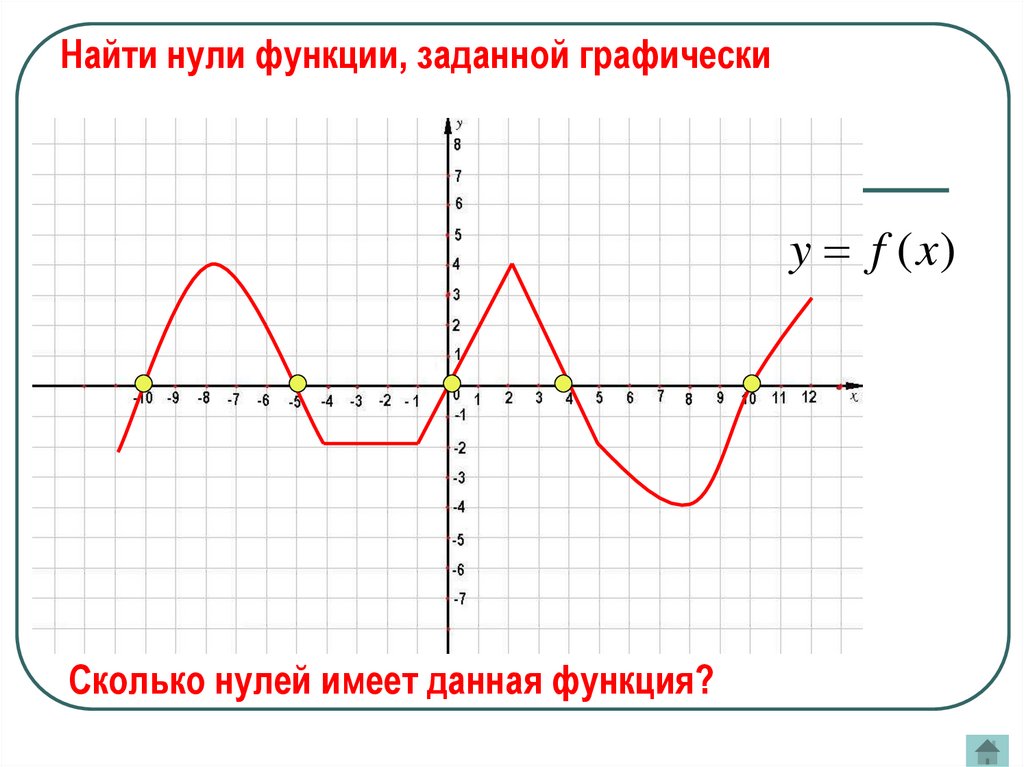
3.
Найти нули функции, заданной графическиy f (x)
Сколько нулей имеет данная функция?
4.
Как найти нули функции, заданнойформулой?
y х 36
2
Пример
Так как y 0, то решаем уравнение :
х 36 0
2
х 36
х 6
2
Найдите нули функций:
y хх 7
16
5. Возрастание и убывание функций
Определение возрастающей функцииОпределение убывающей функции
Доказательство возрастания функции
Доказательство убывания функции
Самостоятельная работа
Графики возрастающих функций
Графики убывающих функций
Нахождение промежутков возрастания и убывания
функции по графику
Линейная функция
6.
Определение возрастающей функцииФункция называется возрастающей в некотором
промежутке, если большему значению аргумента из
этого промежутка соответствует большее значение
функции
Должны выполняться условия:
Если х2 x1 , то f ( x2 ) f ( x1 )
или
Если х2 x1 , то f ( x2 ) f ( x1 )
7.
Определение убывающей функцииФункция называется убывающей в некотором
промежутке, если большему значению аргумента из
этого промежутка соответствует большее значение
функции
Должны выполняться условия:
Если х2 x1 , то f ( x2 ) f ( x1 )
или
Если х2 x1 , то f ( x2 ) f ( x1 )
8.
Доказать, что функцияy 2 х 5,
является возрастающей.
Доказательство
Пусть х2 x1. f ( х2 ) 2 x2 5; f ( х1 ) 2 x1 5.
Найдем разность f ( х2 ) f ( x)
f ( х2 ) f ( x1 ) 2 x2 5 (2 x1 5)
2 x2 5 2 x1 5 2 x2 2 x1
2( x2 x1 ) 0, так как x2 x1 и 2 0.
То есть f ( х2 ) f ( x1 ) 0 f ( х2 ) f ( x1 ).
Тогда f ( x) возрастающая функция
по определению. Ч .т.д
9.
Докажите, что функция y2 х 5,
является убывающей.
Доказательство
Пусть х2 x1. f ( х2 ) 2 x2 5;f ( х1 ) 2 x1 5.
Найдем разность f ( х2 ) f ( x)
f ( х2 ) f ( x1 ) ?
2
То есть f ( х2 ) f ( x1 ) ? 0 f ( х2 ) ? f ( x1 ).
Тогда f ( x) ? функция
по определению. Ч .т.д
10.
Самостоятельная работаДокажите, что функция y
3х 1,
является возрастающей.
Доказательство
11.
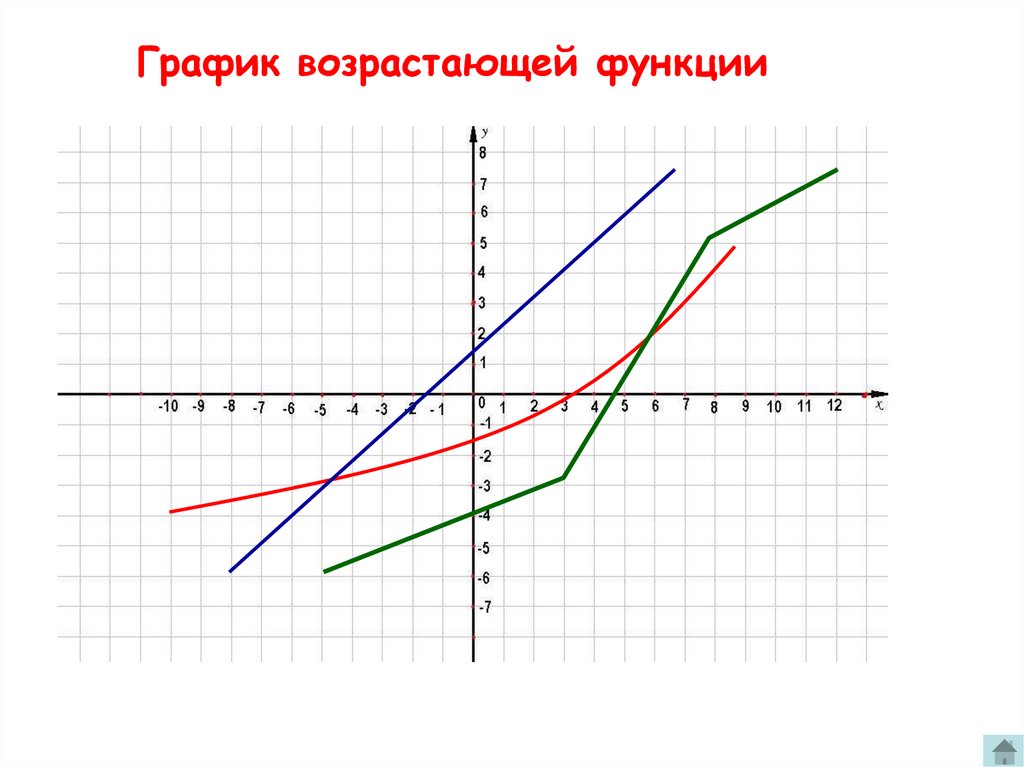
График возрастающей функции12.
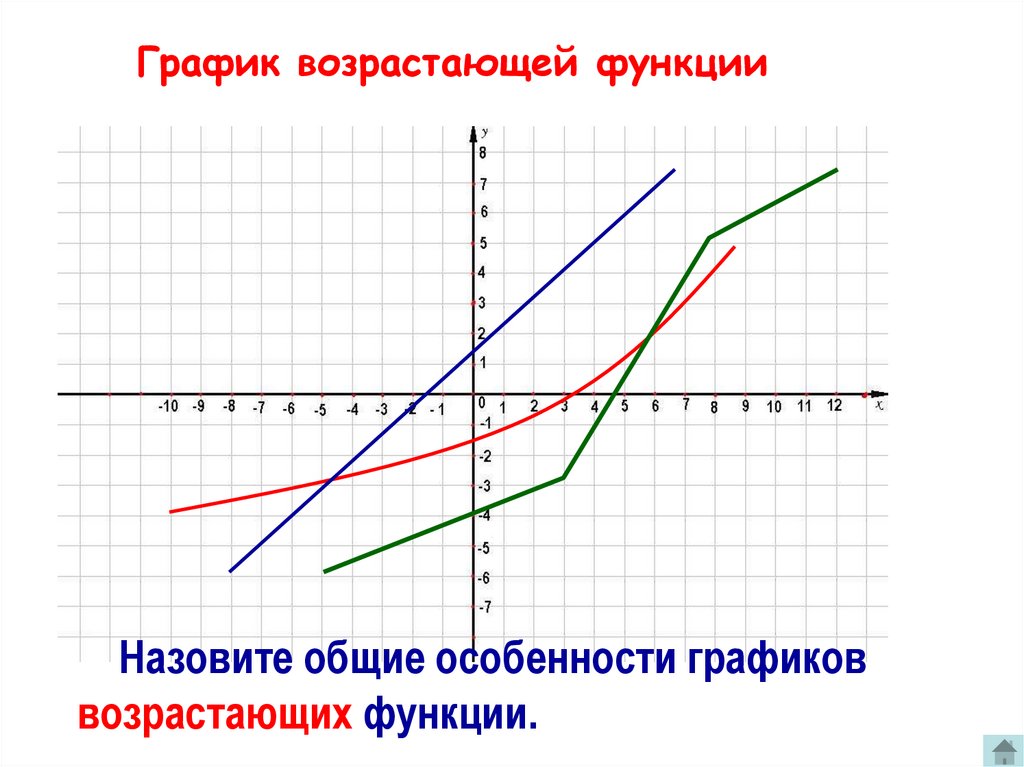
График возрастающей функцииНазовите общие особенности графиков
возрастающих функции.
13.
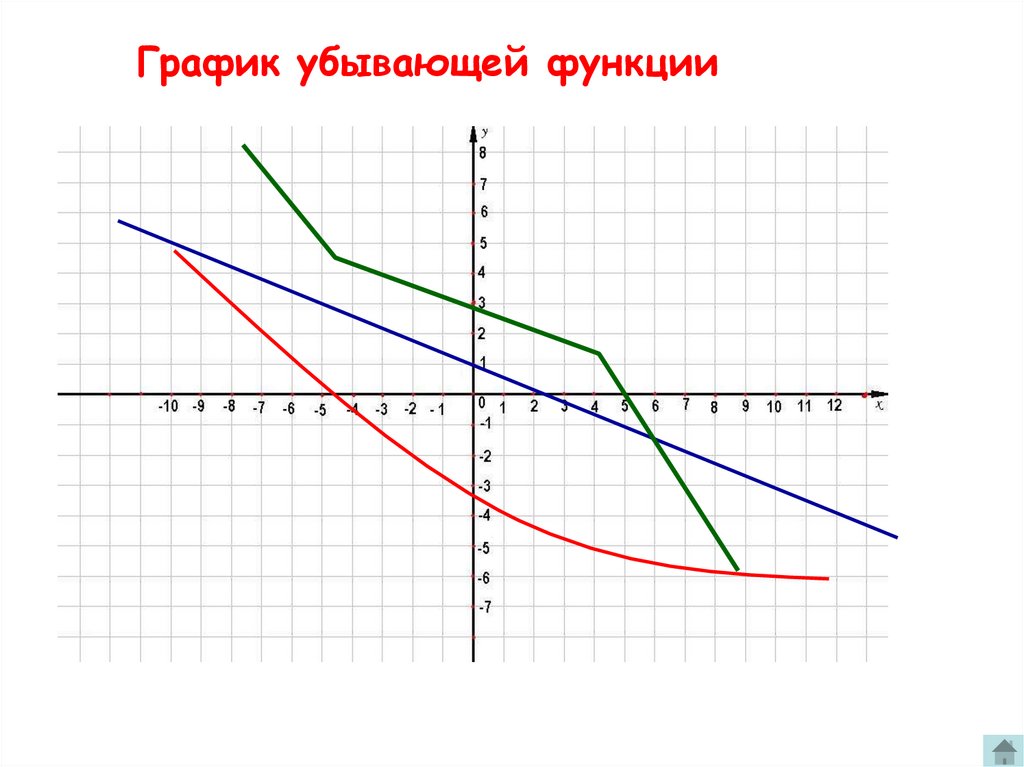
График убывающей функции14.
График убывающей функцииНазовите общие особенности графиков
убывающих функции.
15.
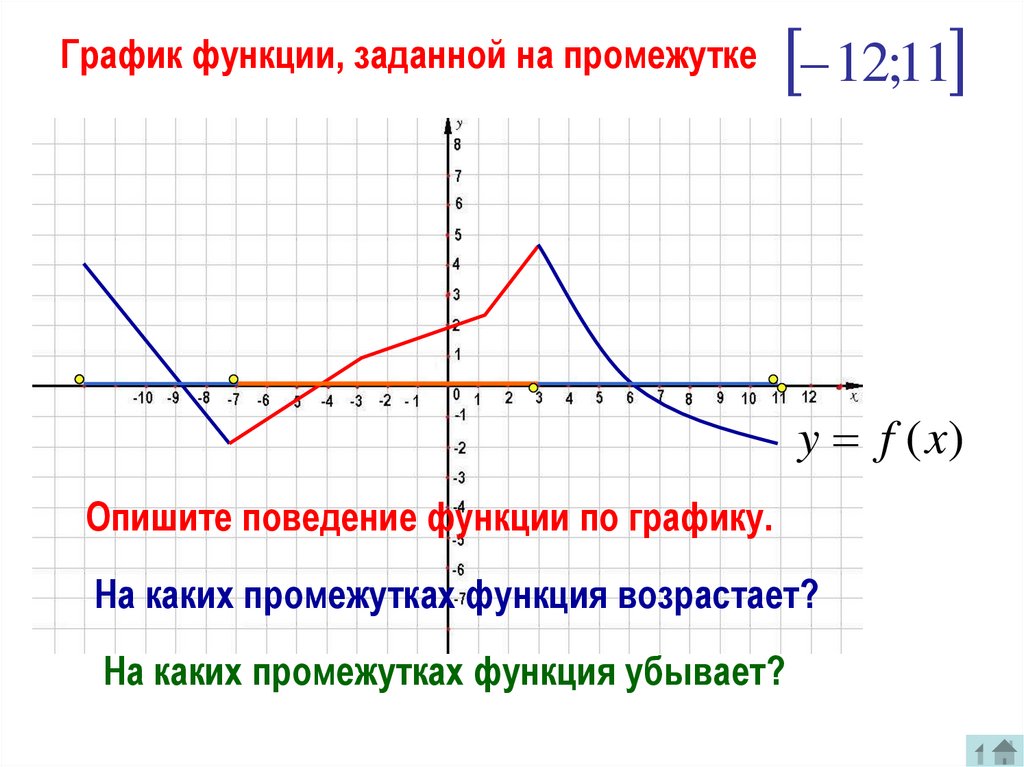
График функции, заданной на промежутке12;11
y f (x)
Опишите поведение функции по графику.
На каких промежутках функция возрастает?
На каких промежутках функция убывает?
16.
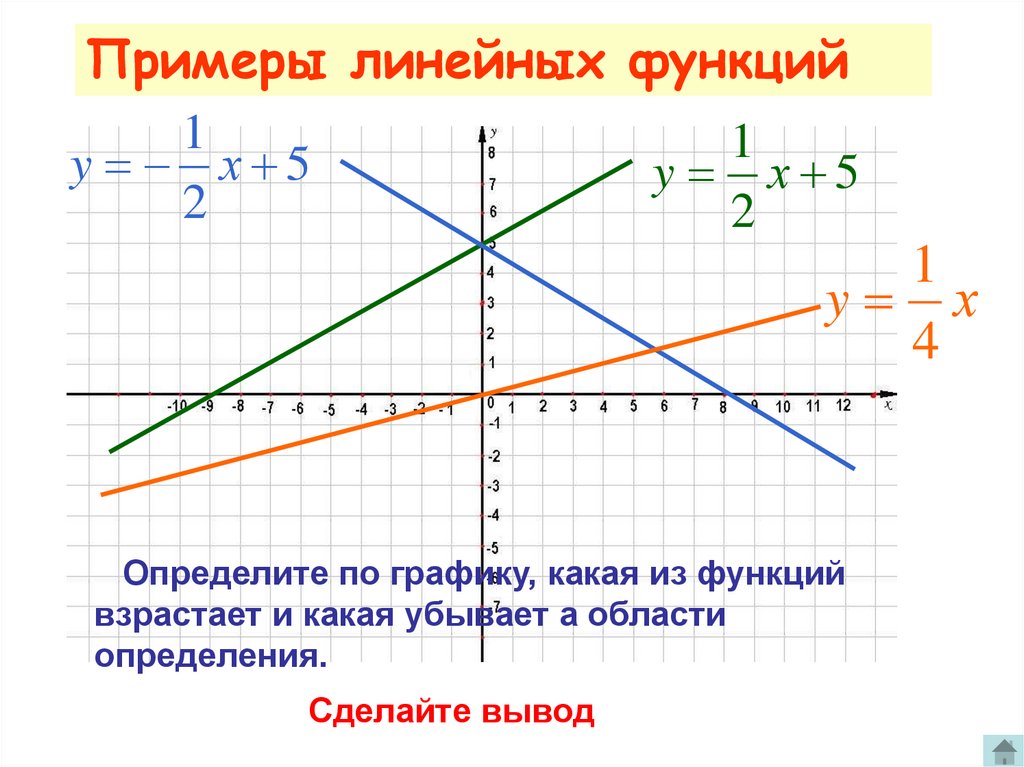
Примеры линейных функций1
1
y х 5
y х 5
2
2
1
y х
4
Определите по графику, какая из функций
взрастает и какая убывает а области
определения.
Сделайте вывод









 mathematics
mathematics








