Исследование функции на монотонность. Алгебра. 8 класс

1.

2.

Определять возрастает или убывает функция, мы уже пробовали и
раньше.
Двигаясь по графику слева на право, если функция так же двигалась
снизу-вверх, мы говорили, что функция возрастает, если же наоборот – сверху вниз, то функция убывала.
Такое определение, со строгой математической точки зрения не подходит,
да и график это всего лишь иллюстрация зависимости функции от переменой.
Поиск промежутков возрастания
исследованием функции на монотонность.
и
убывания
функции
называется
Давайте введем строгие определения возрастающих и убывающих
функций.

3.

Определение. Функцию y=f(x) называют возрастающей на промежутке Х,
если из неравенства ,
здесь точки х1 и х2 любые из промежутка Х.
Другими словами, если всякому большему значению переменой из
промежутка Х, соответствует большее значение функции, то такая функция будет
возрастающей.
Определение. Функцию y=f(x) называют убывающей на промежутке Х,
если из неравенства ,
здесь точки х1 и х2 любые из промежутка Х.
Другими словами, если всякому большему значению переменой из
промежутка Х, соответствует меньшее значение функции, то такая функция будет
убывающей.

4.

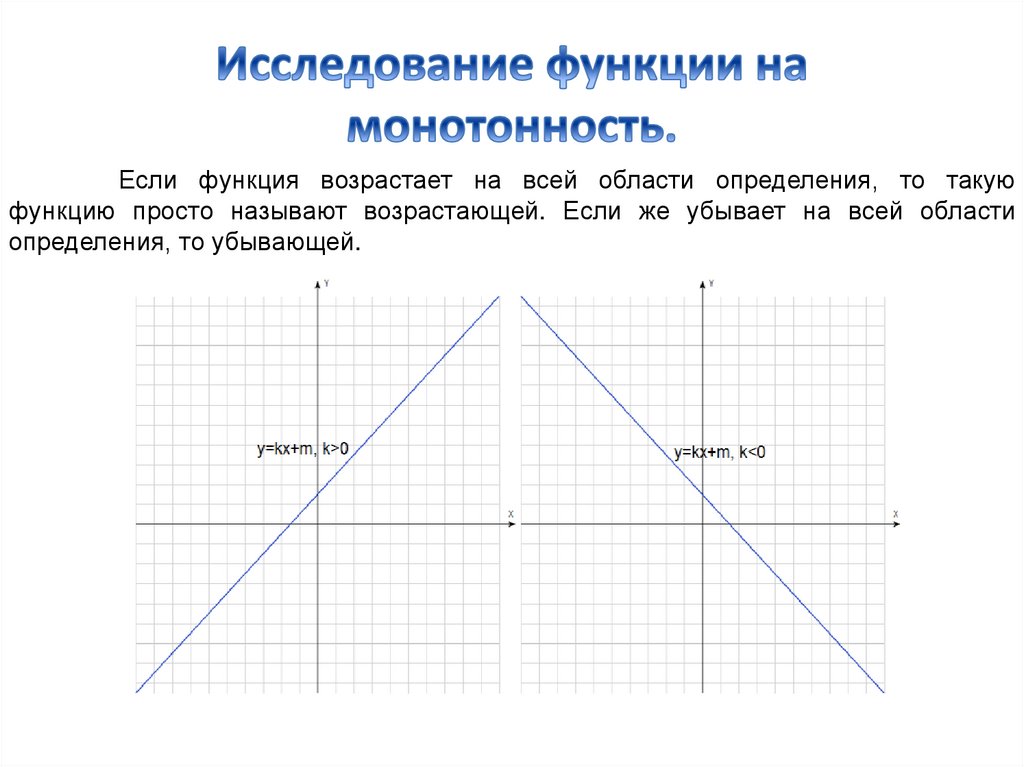
1. Линейная функция y=kx+m.
Если k>0, то функция y=kx+m – возрастает на всей области определения.
Если k<0, то функция y=kx+m – убывает на всей области определения.
Давайте докажем наше утверждения используя определения выше.
Для случая k>0. Рассмотрим два значения аргумента такие, что
,
тогда согласно свойствам неравенствам
(помножив на положительное число, знак неравенства не меняется).
Теперь воспользуемся другим свойством, прибавив любое одинаковое число к
левой и правой части знак не меняется, то есть
но это ведь означает f(x1)<f(x2), что и означает возрастание функции.
Ребята, для случая k<0 докажите сами, это окажется полезным для вас!

5.

Если функция возрастает на всей области определения, то такую
функцию просто называют возрастающей. Если же убывает на всей области
определения, то убывающей.

6.

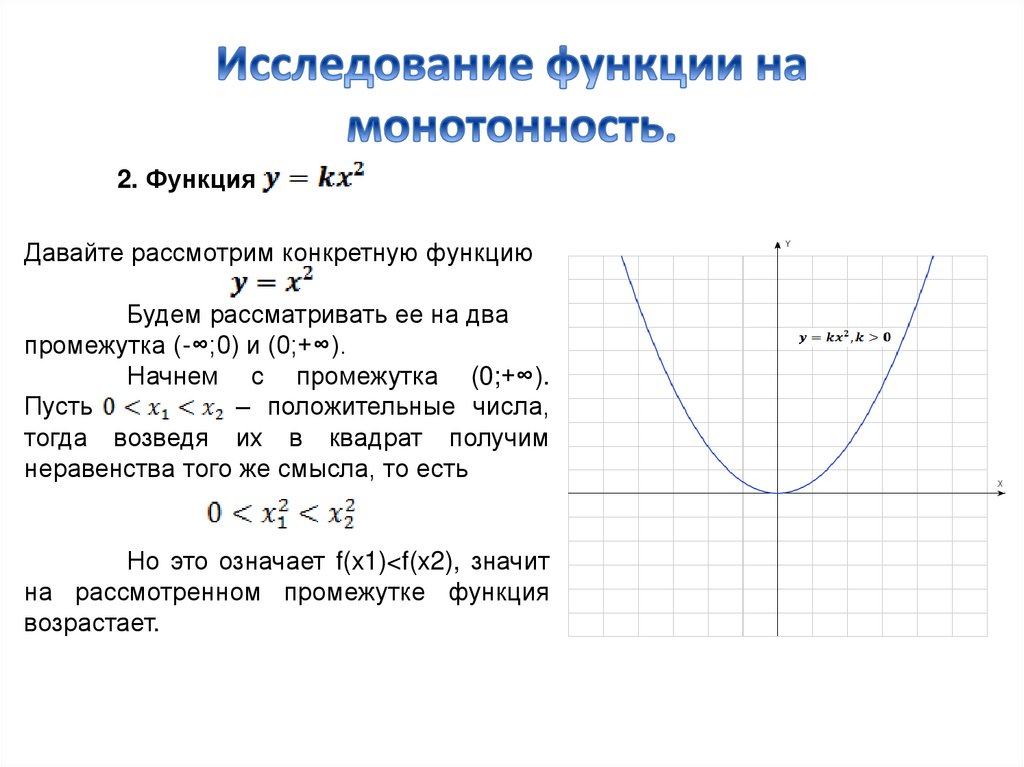
2. Функция
Давайте рассмотрим конкретную функцию
Будем рассматривать ее на два
промежутка (-∞;0) и (0;+∞).
Начнем с промежутка (0;+∞).
Пусть
– положительные числа,
тогда возведя их в квадрат получим
неравенства того же смысла, то есть
Но это означает f(x1)<f(x2), значит
на рассмотренном промежутке функция
возрастает.

7.

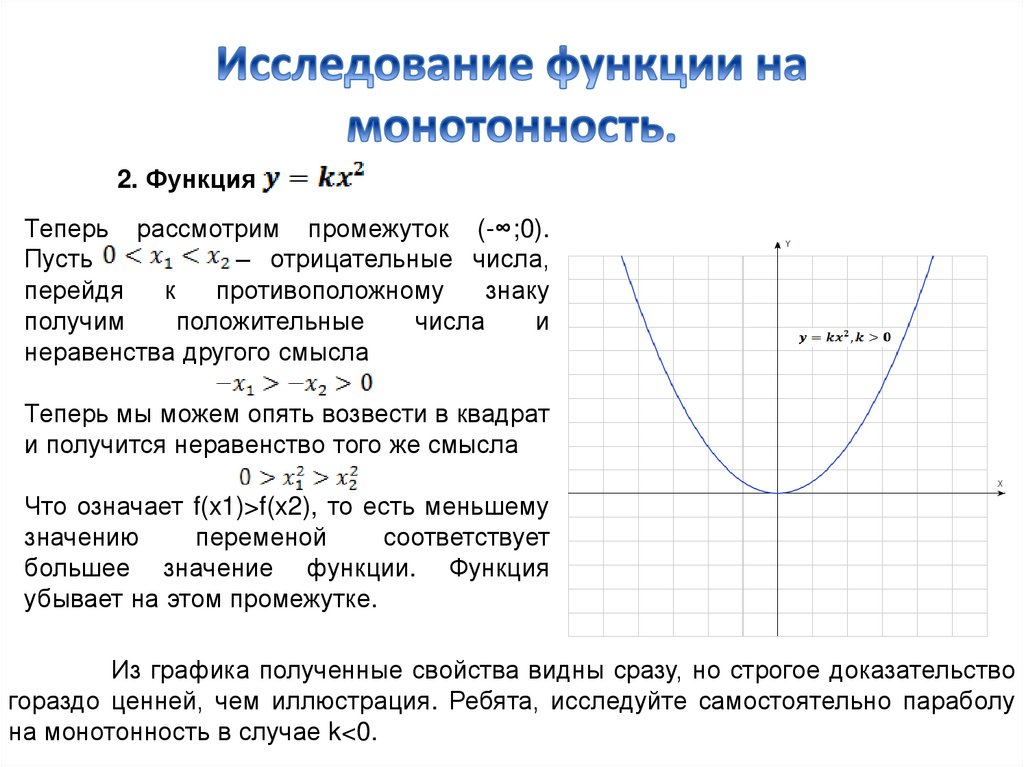
2. Функция
Теперь рассмотрим промежуток (-∞;0).
Пусть
– отрицательные числа,
перейдя
к
противоположному
знаку
получим
положительные
числа
и
неравенства другого смысла
Теперь мы можем опять возвести в квадрат
и получится неравенство того же смысла
Что означает f(x1)>f(x2), то есть меньшему
значению
переменой
соответствует
большее значение функции. Функция
убывает на этом промежутке.
Из графика полученные свойства видны сразу, но строгое доказательство
гораздо ценней, чем иллюстрация. Ребята, исследуйте самостоятельно параболу
на монотонность в случае k<0.

8.

3. Функция
Опять же давайте рассмотрим самый просто случай, при k=1.
Рассмотрим два промежутка хϵ (-∞;0) и xϵ (0;+∞).
Начнем с промежутка (0;+∞). Пусть
–
положительные
числа, когда мы рассматривали неравенства, мы уточнили что в случае
положительных чисел, разделив единицу на них, получится неравенство
противоположного смысла, то есть
Но это означает f(x1)>f(x2), то есть функция убывает на этом промежутке.
Рассмотрим промежуток (-∞;0). Пусть
–отрицательные числа,
перейдя к противоположному знаку получим положительные числа и неравенства
другого смысла
но тогда
Большему значению аргумента соответствует меньшее значение функции.
Гипербола на рассмотренном промежутке убывает.

9.

Так и для любых k>0, можно доказать что гипербола на рассмотренных
промежутках будет иметь те же промежутки монотонности.

10.

4. Функция
В этот раз даже строить график не будем, область определения функции
корня D(y)=[0;+∞) , то есть все числа из области определения положительные.
Рассмотрим
давайте докажем, что f(x1)<f(x2) или
Так как х1 и х2 положительные числа мы можем возводить их в квадрат и
неравенство будет того же смысла
или х1<x2, что соответствует действительности. Таким образом функция
корня квадратного – возрастающая функция.

11.

Пример. Построить и прочитать график функции
Решение. Будем строить графики на соответствующих промежутках,
заметим, что график функции
получается из графика
сдвигом на одну единицу влево и три единицы вверх.

12.

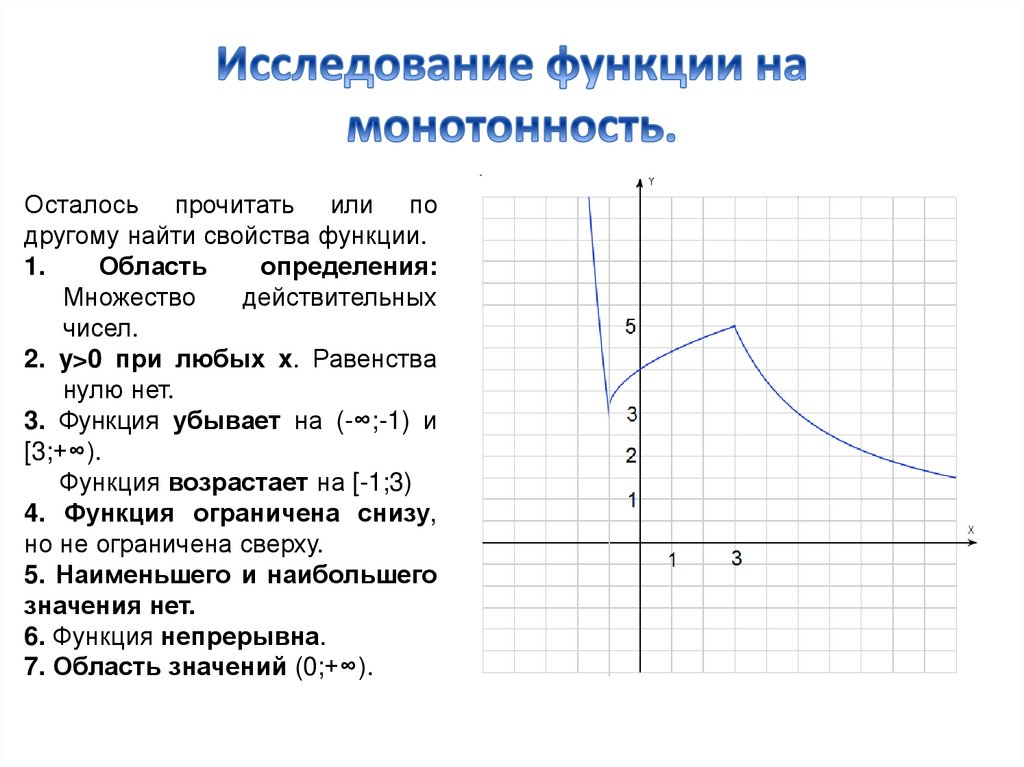
Осталось прочитать или по
другому найти свойства функции.
1.
Область
определения:
Множество
действительных
чисел.
2. y>0 при любых x. Равенства
нулю нет.
3. Функция убывает на (-∞;-1) и
[3;+∞).
Функция возрастает на [-1;3)
4. Функция ограничена снизу,
но не ограничена сверху.
5. Наименьшего и наибольшего
значения нет.
6. Функция непрерывна.
7. Область значений (0;+∞).

13.

Задачи для самостоятельного решения.
1. Исследовать на монотонность
2. Исследовать на монотонность
3. Исследовать на монотонность
4. Построить и прочитать график функции