Исследование функции на монотонность и экстремумы

1. Тема: «Исследование функции на монотонность и экстремумы»

2.

Определение
возрастающей функции
функции
Определение возрастающей
Функция называется возрастающей в некотором
промежутке, если большему значению аргумента из
Функция называется возрастающей в некотором
этого промежутка соответствует большее значение
функции
промежутке, если большему значению аргумента из
этого промежутка
соответствует
большее
значение
Должны
выполняться
условия:
функции
Если х2 x1 , то f ( x2 ) f ( x1 )
или
Должны выполняться
условия:
Если х2 x1 , то f ( x2 ) f ( x1 )
Если х2 x1 , то f ( x2 ) f ( x1 )
или
Если х2 x1 , то f ( x2 ) f ( x1 )

3.

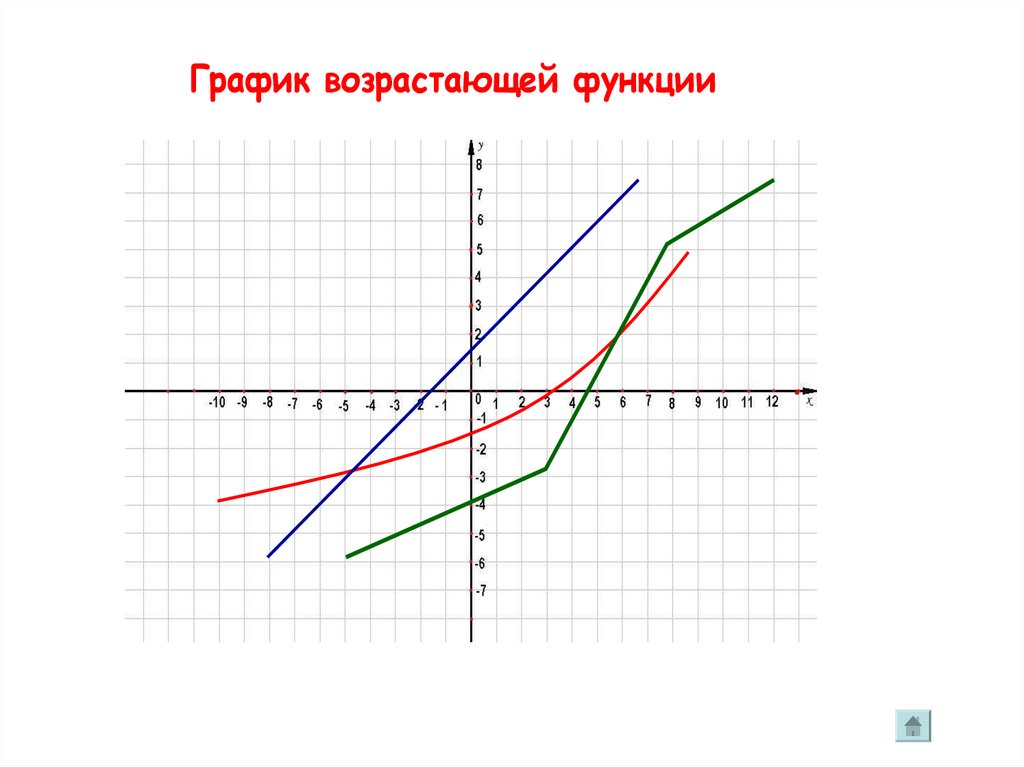
График возрастающей функции

4.

Определение
возрастающей
Определение
убывающейфункции
функции
Функция называется возрастающей в некотором
промежутке,
если большему
значению
аргумента из
Функция
называется
убывающей
в
некотором
этого промежутка соответствует большее значение
функции
промежутке, если большему значению аргумента из
этого промежутка
соответствует
меньшее
значение
Должны
выполняться
условия:
функции
Если х2 x1 , то f ( x2 ) f ( x1 )
или
Должны выполняться
условия:
Если х2 x1 , то f ( x2 ) f ( x1 )
Если х2 x1 , то f ( x2 ) f ( x1 )
или
Если х2 x1 , то f ( x2 ) f ( x1 )

5.

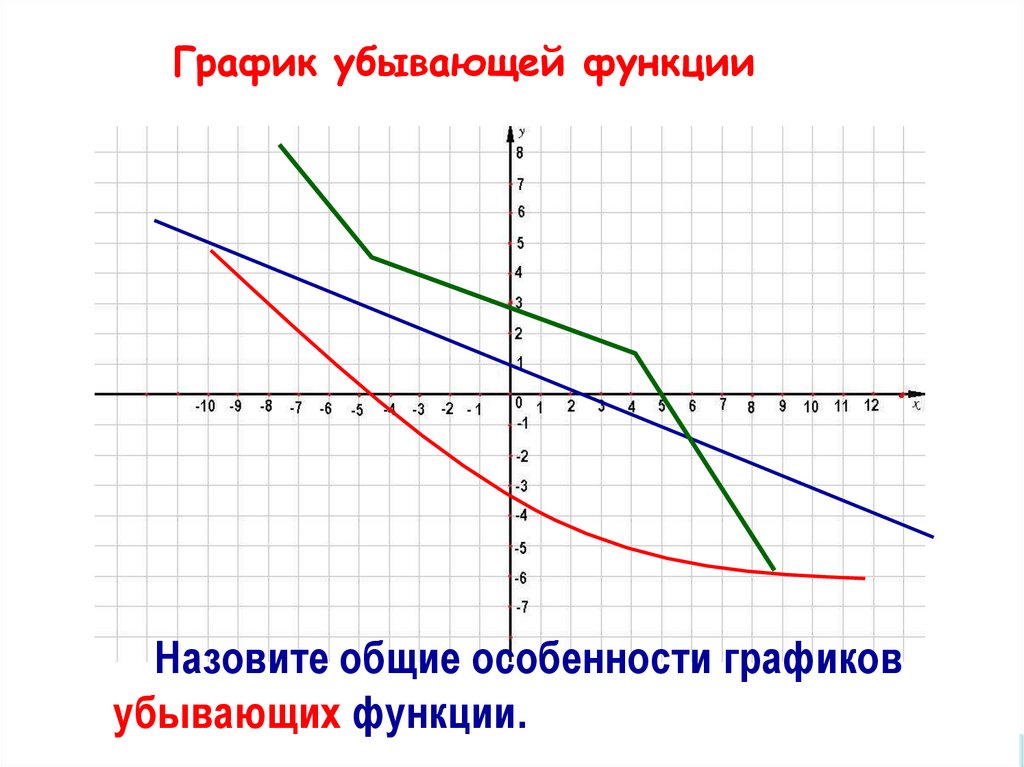
Графикграфик
убывающей
функции
Рассмотрим
убывающей функции
Назовите общие особенности графиков
убывающих функции.

6.

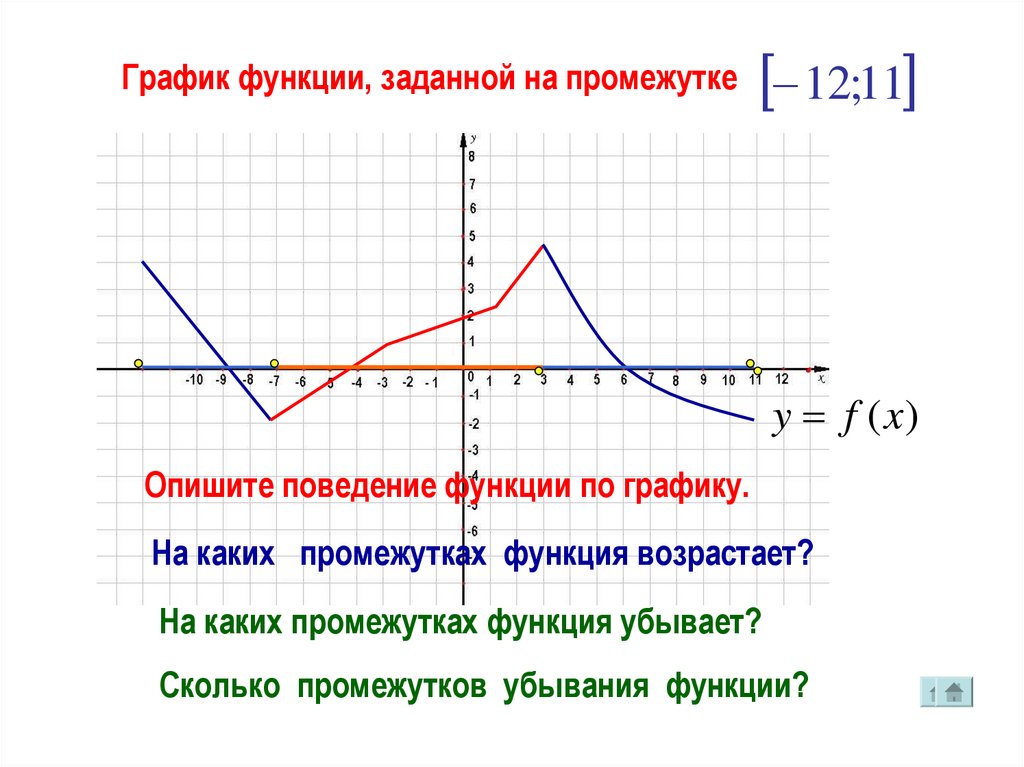
График функции, заданной на промежутке
12;11
y f (x)
Опишите поведение функции по графику.
На каких промежутках функция возрастает?
На каких промежутках функция убывает?
Сколько промежутков убывания функции?

7.

8.

9.

10.

11.

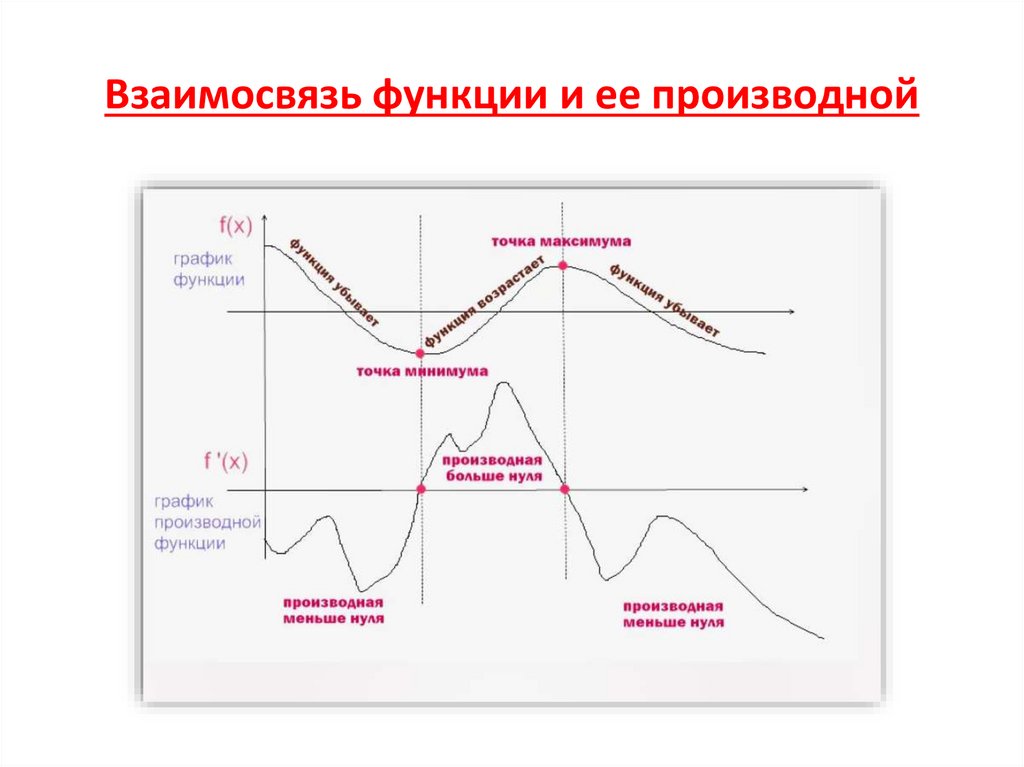
12. Взаимосвязь функции и ее производной

13.

14.

15.

16.

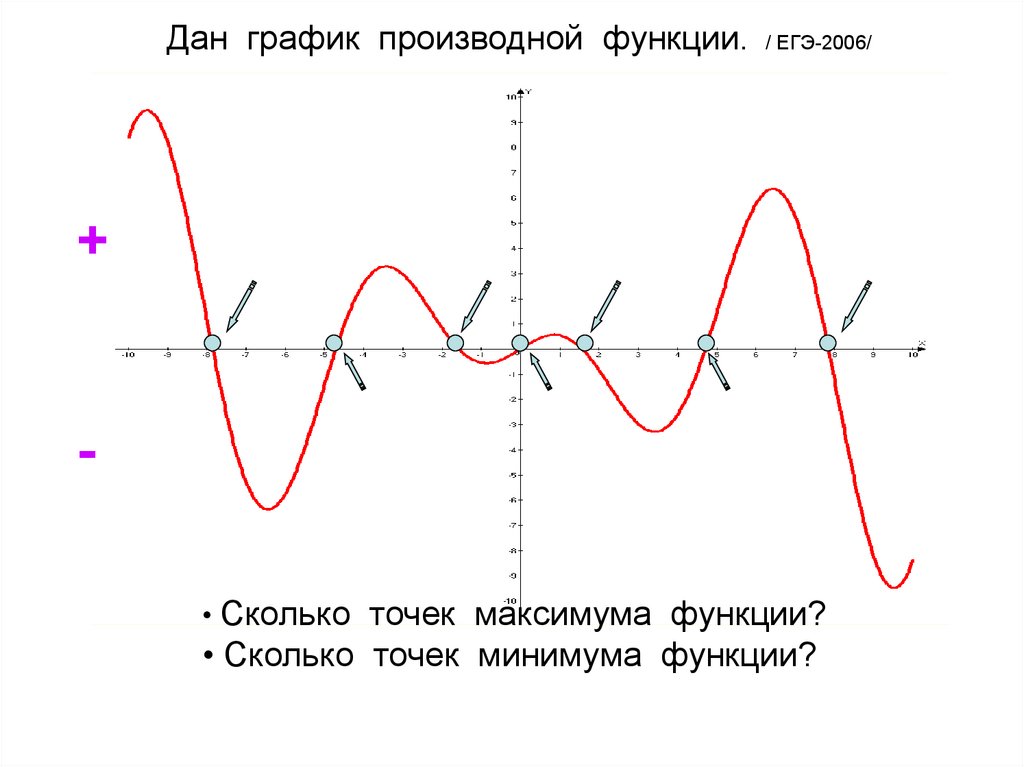
Дан график производной функции. / ЕГЭ-2006/
+
• Сколько точек максимума функции?
• Сколько точек минимума функции?