Similar presentations:
Кинематика. Равномерное движение
1. Кинематика. Равномерное движение
ФизикаКинематика.
Равномерное движение
2.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
3.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
4.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
5.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
6.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
7.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
8.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
9.
ВведениеКинематика – раздел механики, в котором рассматриваются способы описания
механического движения тел без выяснения причин изменения характера их
движения.
Механическое движение – изменение положения тела или его частей
пространстве относительно других тел с течением времени.
в
Прямолинейное движение тела называют равномерным, если тело за любые
равные промежутки времени проходит равные расстояния в одном и том же
направлении.
Способы описания механического движения:
1. Графический
2. Табличный
3. Аналитический
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
10.
Задание 1©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
11.
Задание 1Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
12.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
13.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
14.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
15.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
16.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
17.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
18.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
19.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
20.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
21.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
22.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
Координата в
начальный момент
времени t=0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
23.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Пример:
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
Координата в
начальный момент
времени t=0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
24.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Изменение
Пример:
координаты на 1 с
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
Координата в
начальный момент
времени t=0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
25.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Изменение
Время движения
Пример:
координаты на 1 с
от t=0 до t
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
Координата в
начальный момент
времени t=0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
26.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Изменение
Время движения
Пример:
координаты на 1 с
от t=0 до t
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
Координата в
начальный момент
времени t=0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
27.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
Изменение
Время движения
Пример:
координаты на 1 с
от t=0 до t
х3 = 10 + 5 · 3 = 25 м
Координата
тела в момент
времени t=3c
Координата в
начальный момент
времени t=0
Значение
координаты в
момент времени
t=3с
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
28.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
29.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
30.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
31.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
32.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
33.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
34.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
35.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
36.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
37.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
38.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
39.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
40.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
41.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
42.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
43.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
44.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
45.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
46.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
47.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
48.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
49.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
50.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
51.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
52.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
53.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
54.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
55.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
56.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20*10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
57.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
58.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
59.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20*20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
60.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20·20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
61.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20·20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
62.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20·20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м;
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
63.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20·20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м.
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
64.
Задание 1Уравнение движения, ПП
Координата сокола, летящего по прямой от места охоты к своему гнезду, в
системе отсчета, связанной с Землёй, изменяется с течение времени по закону:
x = 600 - 20 ⋅ t, где х измеряется в метрах, t — в секундах.
а) Определите моменты времени, когда координата сокола имела указанные в
таблице значения. Координата сокола, м
300
100
20
0
–20
Момент времени, с
15
25
29
30
31
б) Определите координату сокола в моменты времени 10 с; 20 с; 0,5 мин и
заполните таблицу.
Момент времени, с
10
20
0,5
Координата сокола, м
Закон равномерного движения:
x(t)= x0+ʋхt,
x0-начальная координата тела, [м]
x-конечная координата тела, [м]
ʋх-проекция скорости тела, [м/с]
t-время, [с]
400
200
0
1. x=300м, тогда 300=600 - 20t, 20 t=600-300, 20t=300, t=15с;
2. x=100м, тогда 100=600-20t, 20 t=600-100, 20t=500, t=25с;
3. x=20м, тогда 20=600-20t, 20 t=600-20, 20t=580, t=29с;
4. x=0м, тогда 0=600-20t, 20 t=600,t=30с;
5. x=-20м, тогда -20=600-20t, 20t=600+20, 20t=620, t=31с;
1. t=10с, тогда x=600-20·10=600-200=400м;
2. t=20с, тогда x=600-20·20=600-400=200м;
3. t=0,5мин=0,5·60=30с, тогда x=600-20·30=600-600=0м.
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
65.
Задание 2©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
66.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Закон
движения
Автобус
Легковой автомобиль
0
Грузовой автомобиль
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
67.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Автобус
Легковой автомобиль
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Закон
движения
-2
0
Грузовой автомобиль
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
68.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Закон
движения
0
Грузовой автомобиль
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
69.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
Закон
движения
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
70.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
Закон
движения
0
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
71.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
Закон
движения
0
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
72.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
Закон
движения
0
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
73.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
Закон
движения
0
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
74.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
Закон
движения
0
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
75.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
0
Автобус: x=0 км, x0=-2 км, t=3 мин,
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
76.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
0
Автобус: x=0 км, x0=-2 км, t=3 мин,
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
77.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
0
Автобус: x=0 км, x0=-2 км, t=3 мин,
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
78.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Объект
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
Легковой автомобиль
2
Грузовой автомобиль
3
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
0
Автобус: x=0 км, x0=-2 км, t=3 мин,
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
79.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
80.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
81.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
2
х 2 t
3
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
82.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
2
х 2 t
3
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
83.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
2
х 2 t
3
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
84.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
2
х 2 t
3
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин,
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
85.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
2
х 2 t
3
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
86.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
2
х 2 t
3
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
87.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
Легковой автомобиль
2
0
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
2
х 2 t
3
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
88.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
89.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
90.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
91.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
92.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
0 ( 3) 1
км / мин;
6
2
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
93.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
1
2
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
0 ( 3) 1
км / мин;
6
2
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
94.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
1
2
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
1
0 ( 3) 1
км / мин; х 3 t
2
6
2
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
95.
Задание 2Работа с графиками
На рисунке приведены графики зависимости координаты х от времени t для
автобуса (1), легкового автомобиля (2) и грузового (3) автомобилей. Пользуясь
графиками, определите начальное координаты (х0), изменения координат за
минуту и законы движения автобуса и автомобилей.
Начальная
Изменение
координата х0,
координаты за
км
мин, км/мин
Автобус
-2
2
3
2
х 2 t
3
Легковой автомобиль
2
0
х 2
Грузовой автомобиль
3
1
2
1
х 3 t
2
Объект
x x0
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
Закон
движения
Автобус: x=0 км, x0=-2 км, t=3 мин,
2
х 2 t
3
0 ( 2) 2
км / мин;
3
3
Легковой автомобиль: x=2км, x0=2км, t=3мин, 0км / мин;
х 2
Грузовой автомобиль: x=0 км,x0=3км, t=6мин,
1
0 ( 3) 1
км / мин; х 3 t
2
6
2
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
96.
Задание 3©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
97.
Задание 3На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
98.
Задание 3На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
99.
Задание 3На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
100.
Задание 3На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
101.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
- пермещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
102.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
- пермещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
103.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
- пермещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
104.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
105.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
106.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
107.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке:
2)На втором участке:
3)На третьем участке:
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
108.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м;
2)На втором участке:
3)На третьем участке:
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
109.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м;
2)На втором участке:
3)На третьем участке:
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
110.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м;
2)На втором участке:
3)На третьем участке:
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
111.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м;
2)На втором участке: S х х0 2 2 0 м;
3)На третьем участке:
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
112.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м;
2)На втором участке: S х х0 2 2 0 м;
3)На третьем участке:
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
113.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м;
2)На втором участке: S х х0 2 2 0 м;
3)На третьем участке: S х х0 2,5 2 4,5 м;
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
114.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м; L 1м;
2)На втором участке: S х х0 2 2 0 м;
3)На третьем участке: S х х0 2,5 2 4,5 м;
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
115.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м; L 1м;
2)На втором участке: S х х0 2 2 0 м; L 0м;
3)На третьем участке: S х х0 2,5 2 4,5 м;
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
116.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м; L 1м;
2)На втором участке: S х х0 2 2 0 м; L 0м;
3)На третьем участке: S х х0 2,5 2 4,5 м; L 4,5 м.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
117.
Задание 3Траектория и путь равны при равномерном движении
На рисунке приведён график движения точечного тела. Определите значения
перемещений этого тела и пройдённые им пути за промежутки времени:
1) от 0 до 2 с;
2) от 2 до 4 с;
3) от 4 до 10 с.
Траектория – линия, вдоль которой движется тело.
Путь – это физическая величина, равная расстоянию
пройденному телом вдоль траектории.
Перемещение – это вектор, соединяющий начальное
положение тела в пространстве с его конечным
положением.
1)На первом участке: S х х0 2 1 1м; L 1м;
2)На втором участке: S х х0 2 2 0 м; L 0м;
3)На третьем участке: S х х0 2,5 2 4,5 м; L 4,5 м.
Ответ: 1) 1, 1; 2) 0, 0; 3) -4,5, 4,5.
x x0 S
t
t
х0 - начальная координата тела, [м]
x - конечная координата тела, [м]
S - перемещение тела, [м]
ʋ - скорость тела, [м/с]
t - промежуток времени, [с]
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
118.
Задание 4©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
119.
Задание 4Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
120.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
121.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
122.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
123.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
124.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
125.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
126.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
127.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
х, км
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
128.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
129.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
130.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
131.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
132.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
А
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
133.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
А
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
134.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
А
0
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
135.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
136.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
137.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
138.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
139.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
140.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
141.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
142.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
143.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
144.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
145.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
146.
Задание 4Задача «встреча»
Из города А в город В выехал автобус, одновременно из города В в город А
выехал грузовой автомобиль. Расстояние между городами А и В равно 210 км.
Модуль скорости автобуса равен 20 км/ч, а грузового автомобиля — 50 км/ч. В
какой момент времени после начала движения автобус встретится с
автомобилем?
Алгоритм решения задач «встреча»:
1) Вводим систему отсчета: тело отсчета,
систему координат и часы + рисунок;
2) Определяем начальные координаты
двух тел x01, x02;
3) Используя систему отсчета, находим
скорости двух тел ʋ1,ʋ2;
4) Записываем законы движения двух
тел x1, x2;
5) Записываем условие встречи тех x1=x2
и приравниваем их;
6) Находим время встречи и координату
встречи.
Ответ: 3 ч.
Вводим систему отсчета:
1) выбираем началом отсчета камень в точке А,
от которого начинает свое движение автобус;
2) направляем координатную ось вдоль дороги
в направлении движения автобуса – 0х;
3) включаем часы (секундомер) в момент начала
движения тел.
x1 =0 + 20t;
x2 = 210 - 50t;
x1 = x2;
0 + 20t = 210 - 50t, 70t = 210, t = 3ч.
2
1
В
А
0
210
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
х, км
147.
Задание 5©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
148.
Задание 5По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
149.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
150.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
0
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
151.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
0
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
152.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
0
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
153.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2
0
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
154.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2
0
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
155.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2
0
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
156.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2
0
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
157.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
158.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
159.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
160.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
161.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
162.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
4) х1 120 м 5t, х2 0 7t;
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
163.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
4) х1 120 м 5t, х2 0 7t;
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
164.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
4) х1 120 м 5t, х2 0 7t;
5) х1 х2 ;
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
165.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
4) х1 120 м 5t, х2 0 7t;
5) х1 х2 ;
6)120 5t 0 7t;2t 120, t 60с.
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
166.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
4) х1 120 м 5t, х2 0 7t;
5) х1 х2 ;
6)120 5t 0 7t;2t 120, t 60с.
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
167.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
4) х1 120 м 5t, х2 0 7t;
5) х1 х2 ;
6)120 5t 0 7t;2t 120, t 60с.
2
2
0
1
1
120
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
168.
Задание 5Задача «погоня»
По прямолинейной трассе движутся два велосипедиста. В начальный момент
времени расстояние межу ними составляло 120 м. Модуль скорости первого
велосипедиста равен 5 м/с, а догоняющего — 7 м/с. Сколько времени
потребуется второму велосипедисту, чтобы догнать первого?
1) Вводим систему отсчета:
а) выбираем началом отсчета камень, от которого начинает свое движение второй
велосипедист;
б) направляем координатную ось вдоль дороги в направлении движения велосипедистов
– 0х;
в) включаем часы (секундомер) в момент начала движения тел.
2) х01 120 м и х2 0 м;
3) 1 5м / с, 2 7 м / с;
4) х1 120 м 5t, х2 0 7t;
5) х1 х2 ;
6)120 5t 0 7t;2t 120, t 60с.
2
2
0
1
1
120
х, м
Ответ: 60с.
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
169.
Задание 6©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
170.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
171.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
172.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
0
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
173.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
0
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
174.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
l1
0
l2
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
175.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
l1
0
l2
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
176.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
l1
0
l2
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
177.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
А
l1
В
хАо
0
хDо=l2
l2
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
178.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
А
l1
В
хАо
0
хDо=l2
l2
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
179.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
А
с
l1
В
хАо
0
хDо=l2
l2
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
180.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
В
хАо
0
хDо=l2
l2
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
181.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
182.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
183.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
184.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
185.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
186.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
187.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
xD0 = l2 = 50м, ʋс = 5м/с;
Конечные координаты тел:
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
188.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
189.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
190.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
191.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
192.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
193.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
194.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
195.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени будет длиться обгон, если модуль скорости
катера равен 15 м/с, а его длина равна 5 м?
Вводим систему отсчета:
а) выбираем началом отсчета камень, лежащий напротив точек А и В в момент начала
обгона;
б) направляем координатную ось вдоль дороги в направлении движения тел – 0х;
в) включаем часы (секундомер) в момент начала обгона.
Начальные координаты и скорости тел:
xA0 = 0 м, ʋк = 15 м/с;
хA = хD + l1 = хD+ 5;
хА = хD + 5;
xD0 = l2 = 50м, ʋс = 5м/с;
хА=0+15t;
0 +15t = 50 + 5t + 5;
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
196.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени
будет длиться
обгон,
если модуль скорости
Алгоритм
решения задач
«погоня»:
1) Вводим
катера равен 15 м/с, а его длина равна
5 м? систему отсчета: тело отсчета, систему
координат и часы + рисунок;
Вводим систему отсчета:
2) Определяем начальные координаты двух тел x01,
а) выбираем началом отсчета камень, xлежащий
напротив точек А и В в момент начала
02 (где 1 тело, которое обгоняет);
обгона;
3) Используя систему отсчета, находим скорости
б) направляем координатную ось вдольдвух
дороги
направлении
движения тел – 0х;
тел ʋв1,ʋ
2;
в) включаем часы (секундомер) в момент
начала обгона.
4) Записываем
законы движения двух тел x1, x2;
Начальные координаты и скорости тел:5) Записываем условие окончания обгона x1= x2 + l,
xA0 = 0 м, ʋк = 15 м/с;
где lх – =длина
тела, которое обгоняет;
хА = хD + 5;
A хD + l1 = хD+ 5;
xD0 = l2 = 50м, ʋс = 5м/с;
6) Решаем
хА=0+15t;систему уравнений,
0 +15t находим
= 50 + 5t +время
5;
обгона
и
координату
обгона.
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
197.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени
будет длиться
обгон,
если модуль скорости
Алгоритм
решения задач
«погоня»:
1) Вводим
катера равен 15 м/с, а его длина равна
5 м? систему отсчета: тело отсчета, систему
координат и часы + рисунок;
Вводим систему отсчета:
2) Определяем начальные координаты двух тел x01,
а) выбираем началом отсчета камень, xлежащий
напротив точек А и В в момент начала
02 (где 1 тело, которое обгоняет);
обгона;
3) Используя систему отсчета, находим скорости
б) направляем координатную ось вдольдвух
дороги
направлении
движения тел – 0х;
тел ʋв1,ʋ
2;
в) включаем часы (секундомер) в момент
начала обгона.
4) Записываем
законы движения двух тел x1, x2;
Начальные координаты и скорости тел:5) Записываем условие окончания обгона x1= x2 + l,
xA0 = 0 м, ʋк = 15 м/с;
где lх – =длина
тела, которое обгоняет;
хА = хD + 5;
A хD + l1 = хD+ 5;
xD0 = l2 = 50м, ʋс = 5м/с;
6) Решаем
хА=0+15t;систему уравнений,
0 +15t находим
= 50 + 5t +время
5;
обгона
и
координату
обгона.
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
198.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени
будет длиться
обгон,
если модуль скорости
Алгоритм
решения задач
«погоня»:
1) Вводим
катера равен 15 м/с, а его длина равна
5 м? систему отсчета: тело отсчета, систему
координат и часы + рисунок;
Вводим систему отсчета:
2) Определяем начальные координаты двух тел x01,
а) выбираем началом отсчета камень, xлежащий
напротив точек А и В в момент начала
02 (где 1 тело, которое обгоняет);
обгона;
3) Используя систему отсчета, находим скорости
б) направляем координатную ось вдольдвух
дороги
направлении
движения тел – 0х;
тел ʋв1,ʋ
2;
в) включаем часы (секундомер) в момент
начала обгона.
4) Записываем
законы движения двух тел x1, x2;
Начальные координаты и скорости тел:5) Записываем условие окончания обгона x1= x2 + l,
xA0 = 0 м, ʋк = 15 м/с;
где lх – =длина
тела, которое обгоняет;
хА = хD + 5;
A хD + l1 = хD+ 5;
xD0 = l2 = 50м, ʋс = 5м/с;
6) Решаем
хА=0+15t;систему уравнений,
0 +15t находим
= 50 + 5t +время
5;
обгона
и
координату
обгона.
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
199.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени
будет длиться
обгон,
если модуль скорости
Алгоритм
решения задач
«погоня»:
1) Вводим
катера равен 15 м/с, а его длина равна
5 м? систему отсчета: тело отсчета, систему
координат и часы + рисунок;
Вводим систему отсчета:
2) Определяем начальные координаты двух тел x01,
а) выбираем началом отсчета камень, xлежащий
напротив точек А и В в момент начала
02 (где 1 тело, которое обгоняет);
обгона;
3) Используя систему отсчета, находим скорости
б) направляем координатную ось вдольдвух
дороги
направлении
движения тел – 0х;
тел ʋв1,ʋ
2;
в) включаем часы (секундомер) в момент
начала обгона.
4) Записываем
законы движения двух тел x1, x2;
Начальные координаты и скорости тел:5) Записываем условие окончания обгона x1= x2 + l,
xA0 = 0 м, ʋк = 15 м/с;
где lх – =длина
тела, которое обгоняет;
хА = хD + 5;
A хD + l1 = хD+ 5;
xD0 = l2 = 50м, ʋс = 5м/с;
6) Решаем
хА=0+15t;систему уравнений,
0 +15t находим
= 50 + 5t +время
5;
обгона
и
координату
обгона.
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
200.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени
будет длиться
обгон,
если модуль скорости
Алгоритм
решения задач
«погоня»:
1) Вводим
катера равен 15 м/с, а его длина равна
5 м? систему отсчета: тело отсчета, систему
координат и часы + рисунок;
Вводим систему отсчета:
2) Определяем начальные координаты двух тел x01,
а) выбираем началом отсчета камень, xлежащий
напротив точек А и В в момент начала
02 (где 1 тело, которое обгоняет);
обгона;
3) Используя систему отсчета, находим скорости
б) направляем координатную ось вдольдвух
дороги
направлении
движения тел – 0х;
тел ʋв1,ʋ
2;
в) включаем часы (секундомер) в момент
начала обгона.
4) Записываем
законы движения двух тел x1, x2;
Начальные координаты и скорости тел:5) Записываем условие окончания обгона x1= x2 + l,
xA0 = 0 м, ʋк = 15 м/с;
где lх – =длина
тела, которое обгоняет;
хА = хD + 5;
A хD + l1 = хD+ 5;
xD0 = l2 = 50м, ʋс = 5м/с;
6) Решаем
хА=0+15t;систему уравнений,
0 +15t находим
= 50 + 5t +время
5;
обгона
и
координату
обгона.
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
201.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени
будет длиться
обгон,
если модуль скорости
Алгоритм
решения задач
«погоня»:
1) Вводим
катера равен 15 м/с, а его длина равна
5 м? систему отсчета: тело отсчета, систему
координат и часы + рисунок;
Вводим систему отсчета:
2) Определяем начальные координаты двух тел x01,
а) выбираем началом отсчета камень, xлежащий
напротив точек А и В в момент начала
02 (где 1 тело, которое обгоняет);
обгона;
3) Используя систему отсчета, находим скорости
б) направляем координатную ось вдольдвух
дороги
направлении
движения тел – 0х;
тел ʋв1,ʋ
2;
в) включаем часы (секундомер) в момент
начала обгона.
4) Записываем
законы движения двух тел x1, x2;
Начальные координаты и скорости тел:5) Записываем условие окончания обгона x1= x2 + l,
xA0 = 0 м, ʋк = 15 м/с;
где lх – =длина
тела, которое обгоняет;
хА = хD + 5;
A хD + l1 = хD+ 5;
xD0 = l2 = 50м, ʋс = 5м/с;
6) Решаем
хА=0+15t;систему уравнений,
0 +15t находим
= 50 + 5t +время
5;
обгона
и
координату
обгона.
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
202.
Задание 6Задача «обгон»
Катер обгоняет судно, идущее со скоростью, модуль которого равен 5 м/с. Длина
судна равна 50 м. Сколько времени
будет длиться
обгон,
если модуль скорости
Алгоритм
решения задач
«погоня»:
1) Вводим
катера равен 15 м/с, а его длина равна
5 м? систему отсчета: тело отсчета, систему
координат и часы + рисунок;
Вводим систему отсчета:
2) Определяем начальные координаты двух тел x01,
а) выбираем началом отсчета камень, xлежащий
напротив точек А и В в момент начала
02 (где 1 тело, которое обгоняет);
обгона;
3) Используя систему отсчета, находим скорости
б) направляем координатную ось вдольдвух
дороги
направлении
движения тел – 0х;
тел ʋв1,ʋ
2;
в) включаем часы (секундомер) в момент
начала обгона.
4) Записываем
законы движения двух тел x1, x2;
Начальные координаты и скорости тел:5) Записываем условие окончания обгона x1= x2 + l,
xA0 = 0 м, ʋк = 15 м/с;
где lх – =длина
тела, которое обгоняет;
хА = хD + 5;
A хD + l1 = хD+ 5;
xD0 = l2 = 50м, ʋс = 5м/с;
6) Решаем
хА=0+15t;систему уравнений,
0 +15t находим
= 50 + 5t +время
5;
обгона
и
координату
обгона.
Конечные координаты тел:
хD = 50 + 5t;
10t = 55, t = 5,5с.
xA = xA0 + ʋк · t = 0 +15t;
xD =xD0 + ʋс · t = 50 + 5t;
к
к
А
с
с
l1
С
В
Ответ: 5,5 с.
D
хАо
0
хDо=l2
l2
хD
хА = хD + l1
х, м
©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
203.
Итог©2019 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

































































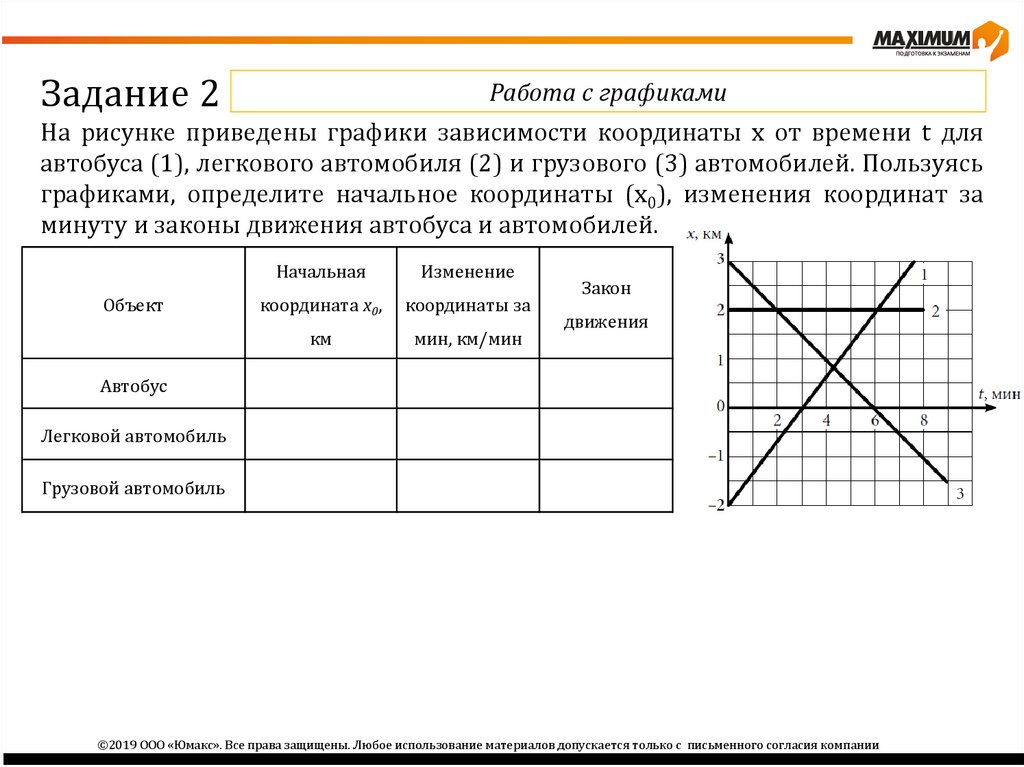




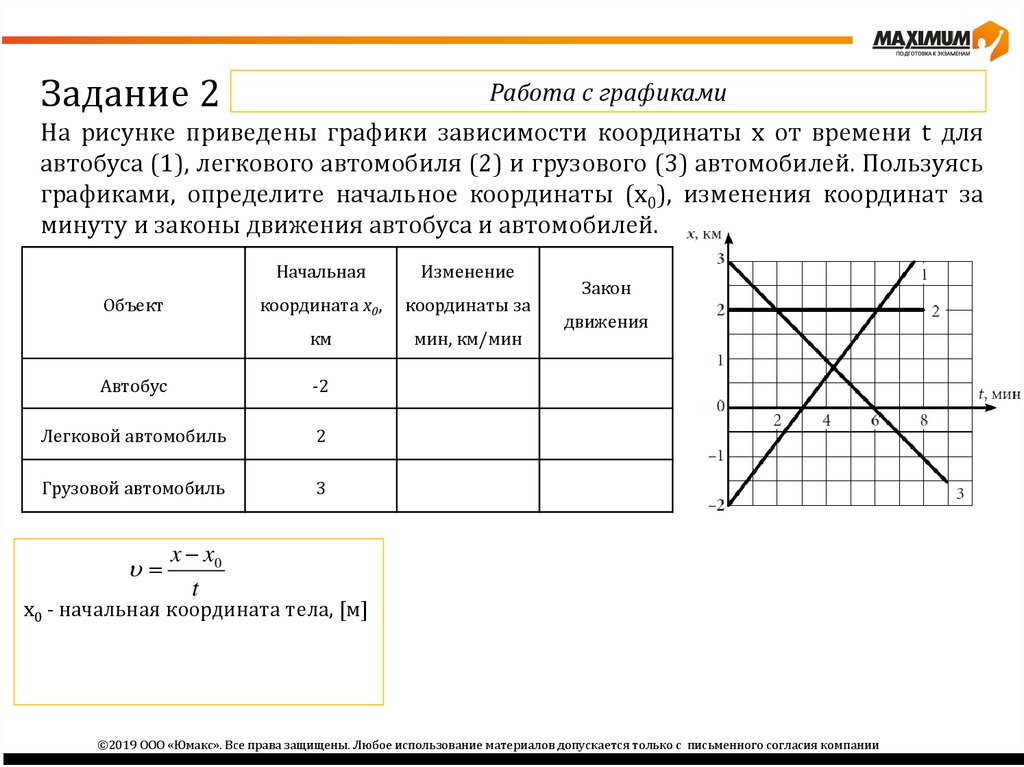




































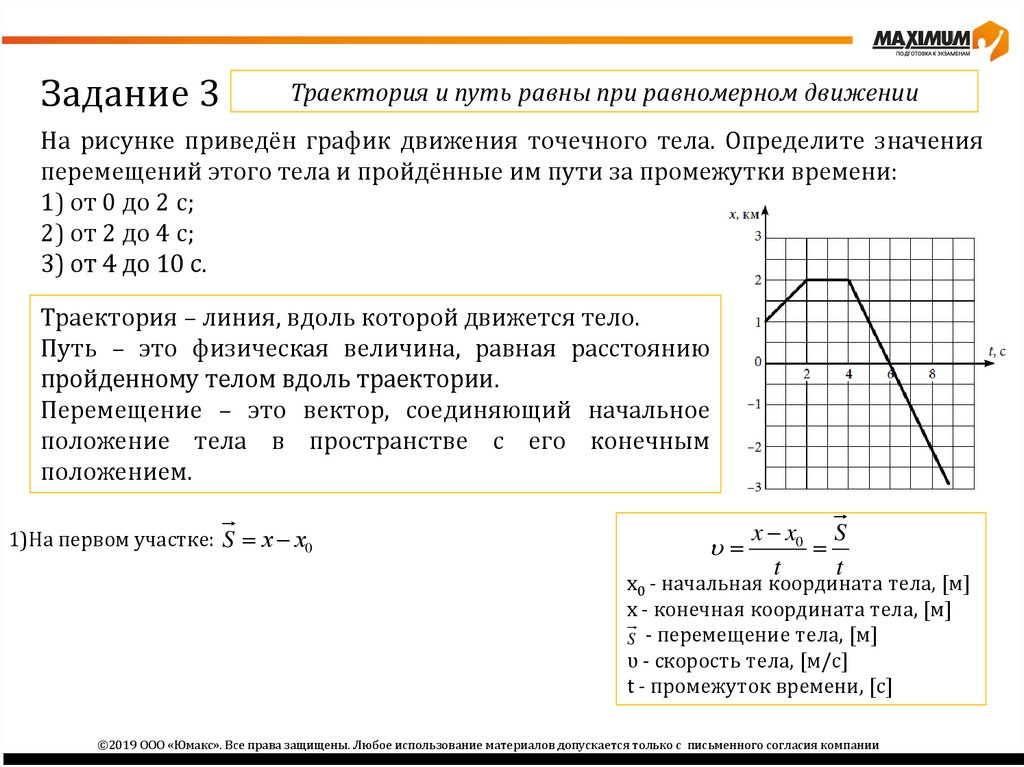







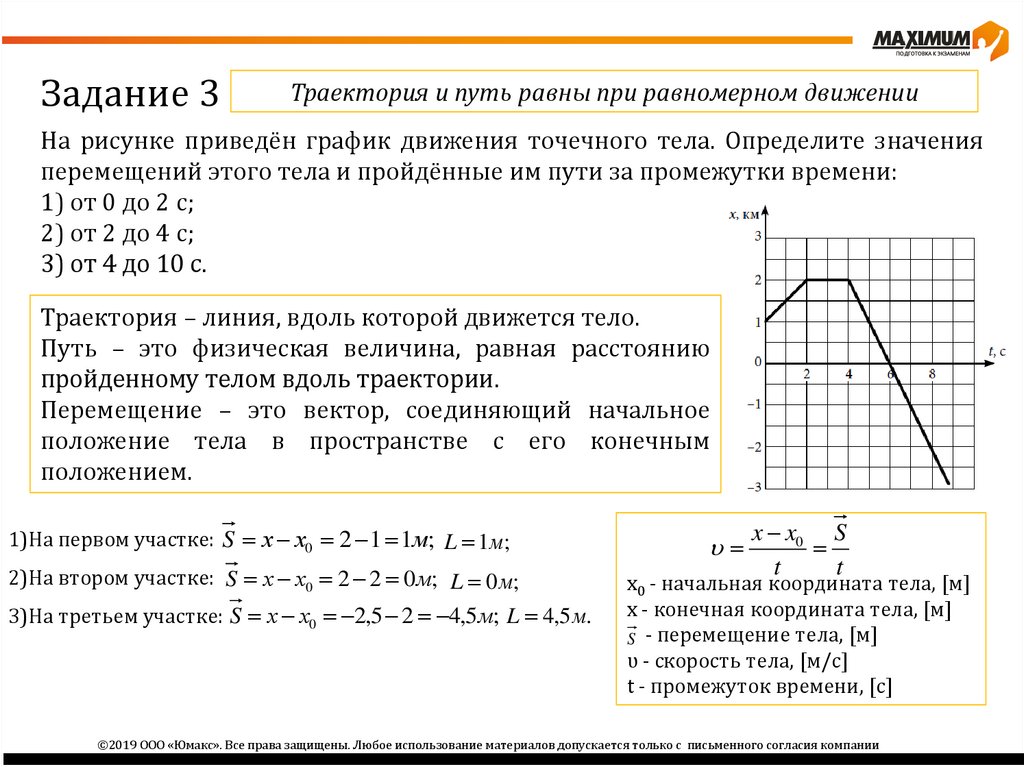















































































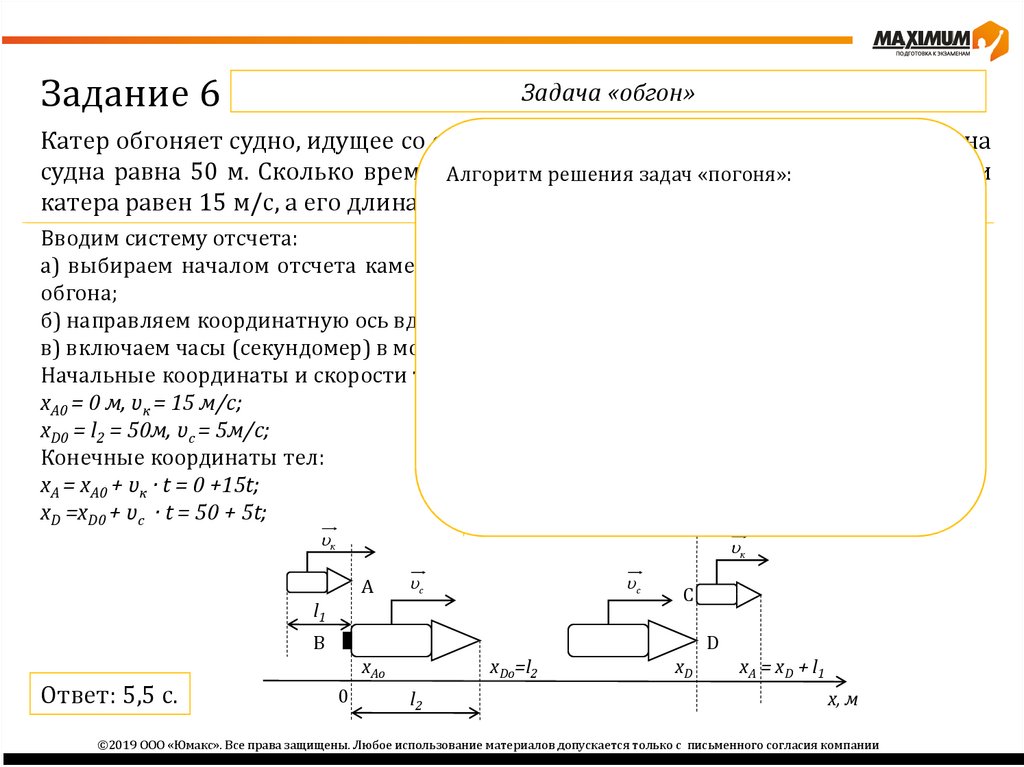
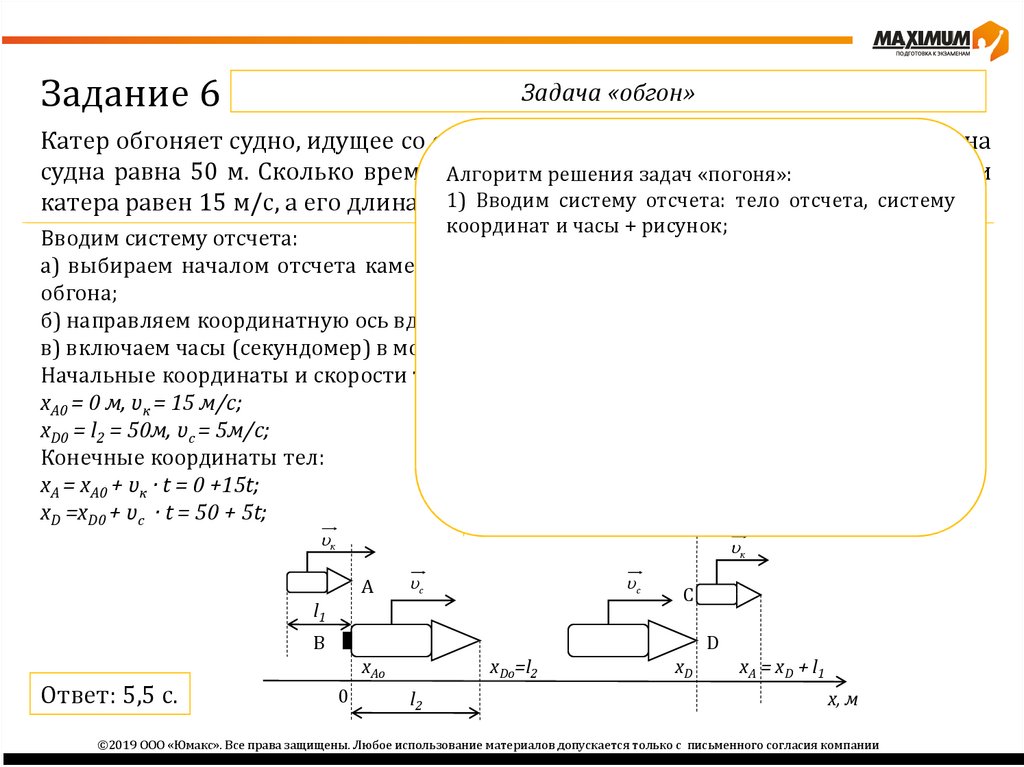



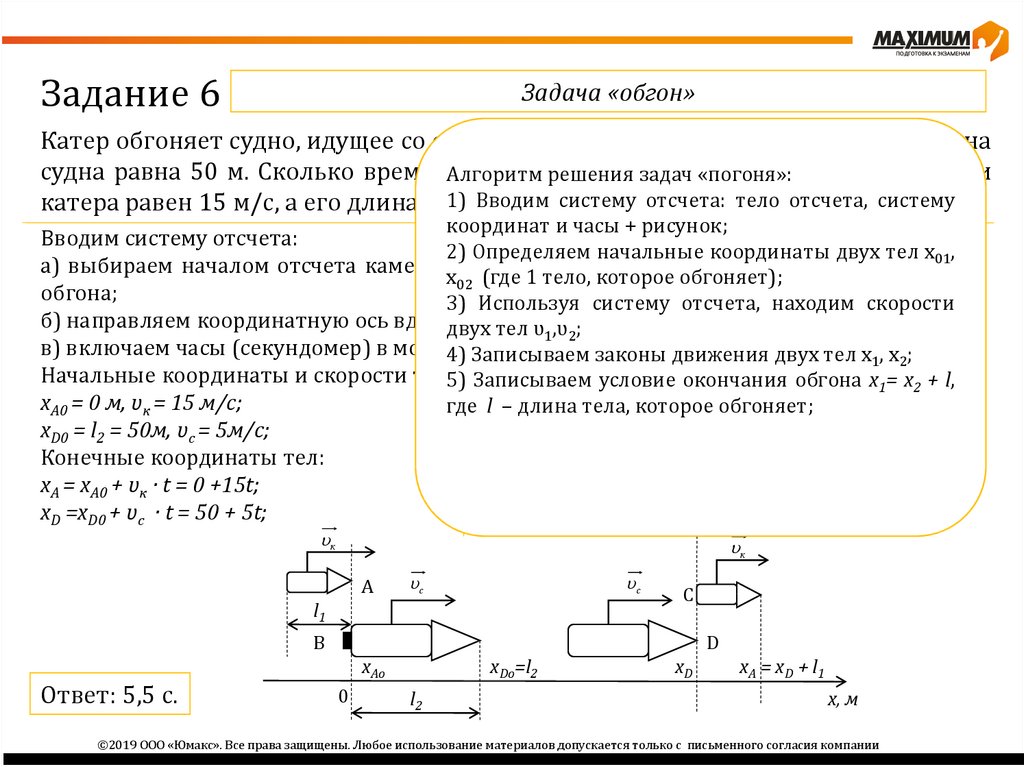


 physics
physics








