Similar presentations:
Инженерная графика. Начертательная геометрия. Конспект лекций
1.
ИНЖЕНЕРНАЯ ГРАФИКАНАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Конспект лекций
Гродно 2011
2.
СОДЕРЖАНИЕПРЕДИСЛОВИЕ
1 ОБОЗНАЧЕНИЯ И СИМВОЛЫ
1.1 ОБОЗНАЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
1.2 СИМВОЛЫ
2 ЛЕКЦИЯ №1. ВВЕДЕНИЕ. ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ
ЛИНИИ
2.1 МЕТОД ПАРАЛЛЕЛЬНОГО ПРЯМОУГОЛЬНОГО ПРОЕЦИРОВАНИЯ
2.2 ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ. КООРДИНАТЫ ТОЧКИ. КОМПЛЕКСНЫЙ
ЧЕРТЕЖ
2.3 ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
3 ЛЕКЦИЯ №2. ЧТЕНИЕ ЧЕРТЕЖА. МЕТРИЧЕСКИЕ
И ПОЗИЦИОННЫЕ ЗАДАЧИ. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
3.1 ЧТЕНИЕ ЧЕРТЕЖА
3.2 ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ И ЕГО УГЛОВ
НАКЛОНА К ПЛОСКОСТЯМ ПРОЕКЦИЙ СПОСОБОМ ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА
3.3 СЛЕДЫ ПРЯМОЙ
3.4 ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
3.5 ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ В ЗАДАННОМ ОТНОШЕНИИ
4 ЛЕКЦИЯ № 3. ПЛОСКОСТЬ. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ
ПЛОСКОСТЕЙ, ПРЯМОЙ И ПЛОСКОСТИ
4.1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ
4.2 СЛЕДЫ ПЛОСКОСТИ
4.3 ПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
4.4 ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ
4.5 ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
3.
5 ЛЕКЦИЯ № 4. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ, ПРЯМОЙ ИПЛОСКОСТИ
5.1 ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
5.2 ПЕРЕСЕКАЮЩИЕСЯ ПЛОСКОСТИ
5.3 ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
5.4 ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
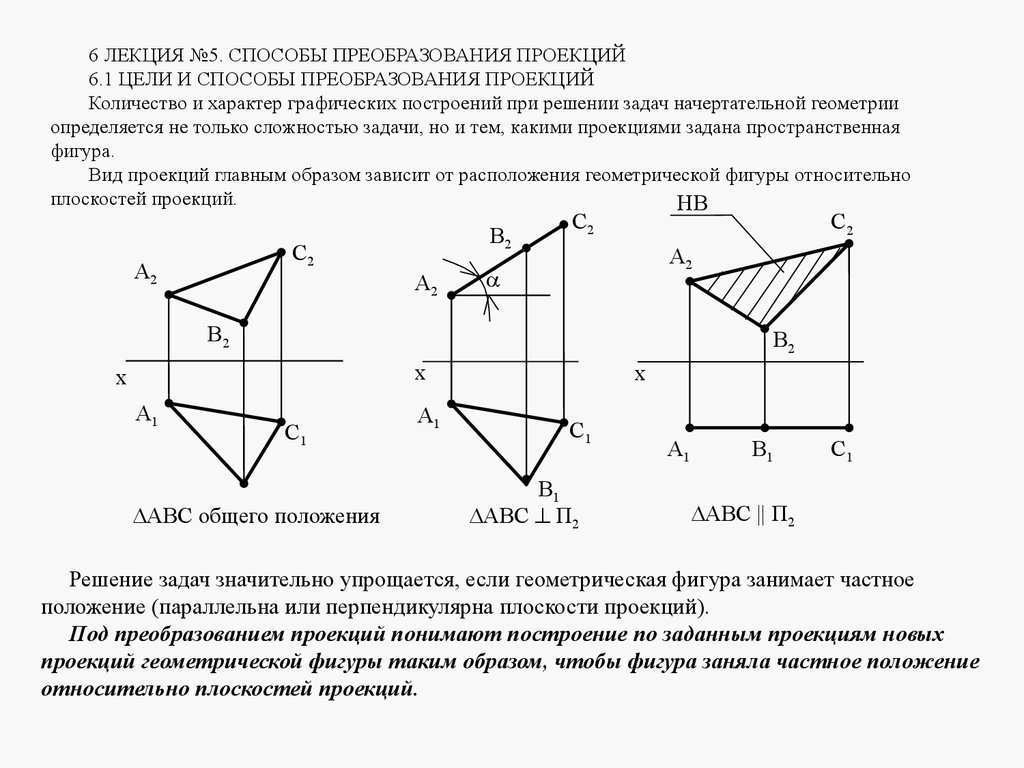
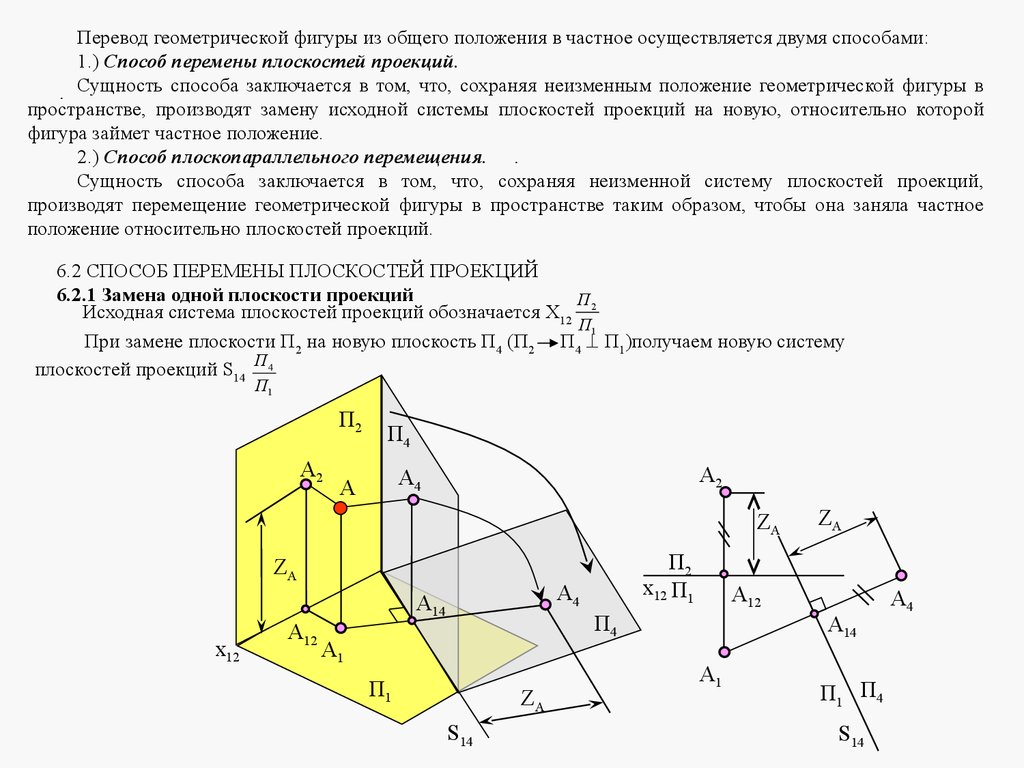
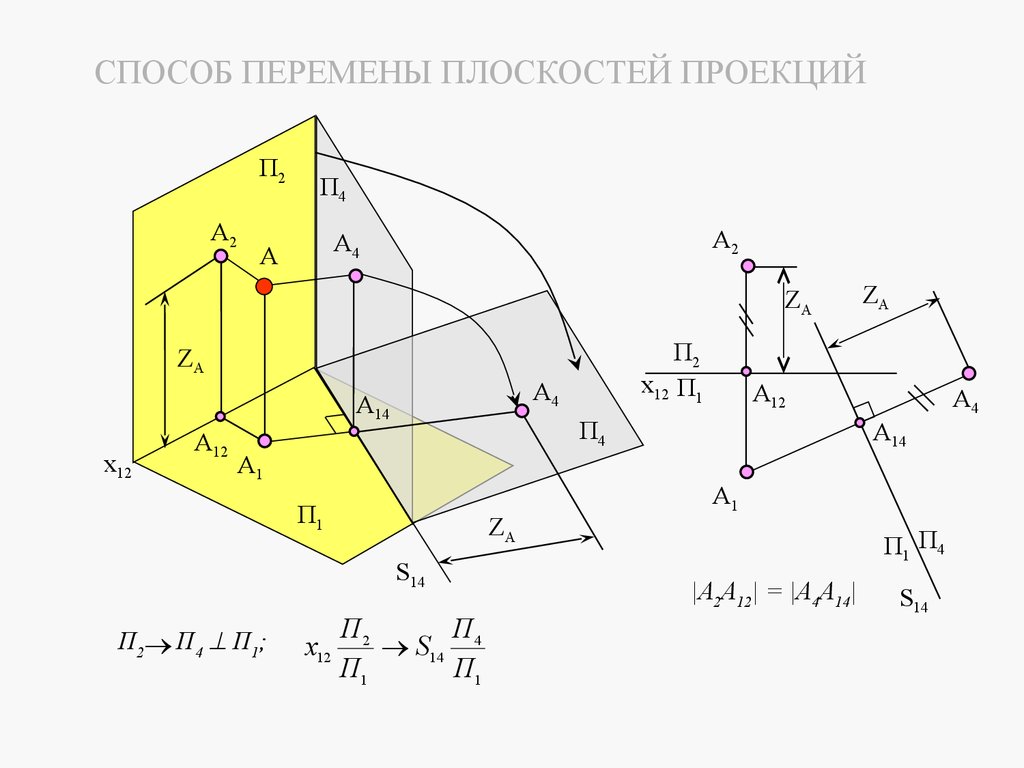
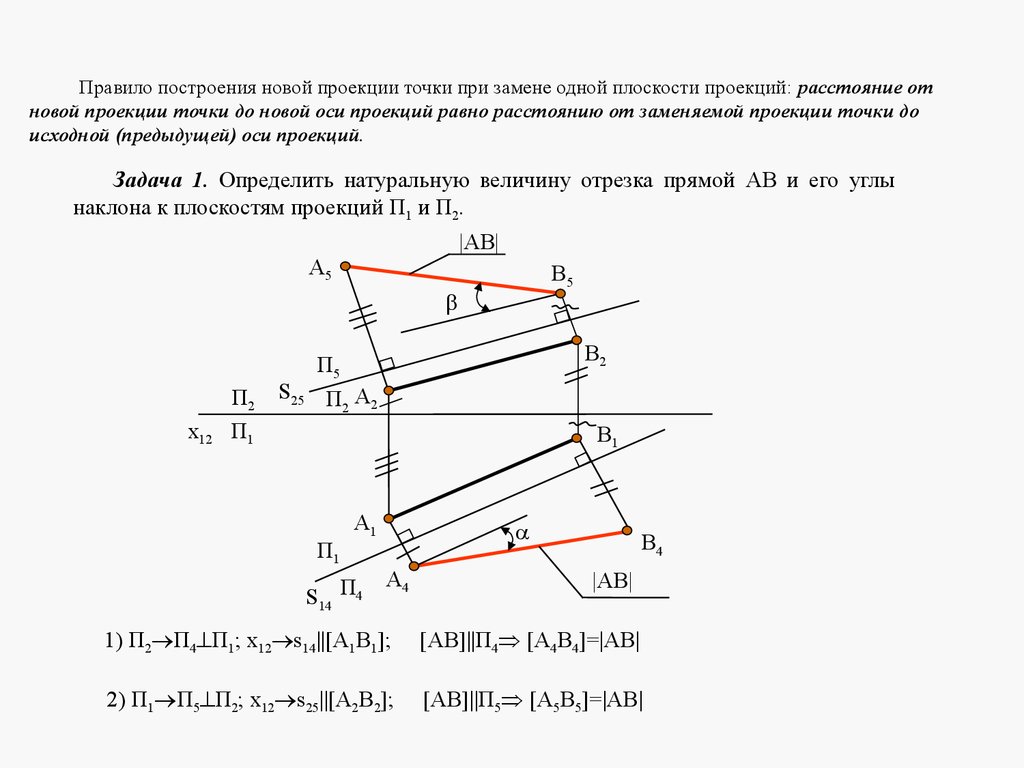
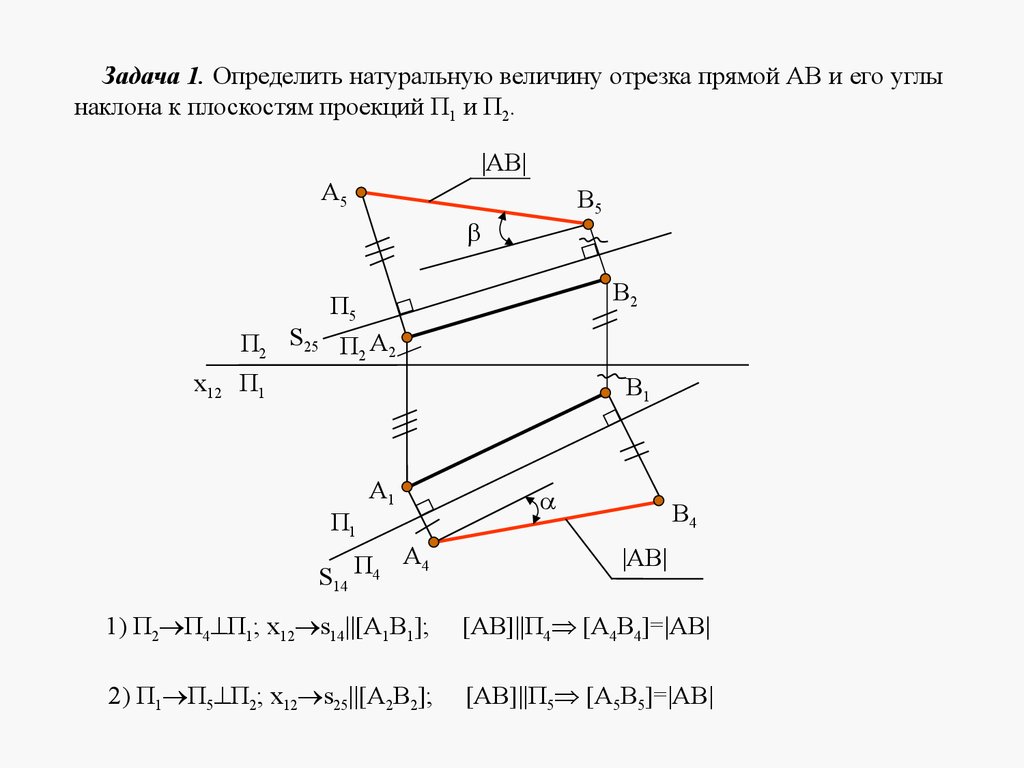
6 ЛЕКЦИЯ №5. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
6.1 ЦЕЛИ И СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ
6.2 СПОСОБ ПЕРЕМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
6.3 СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕМЕЩЕНИЯ
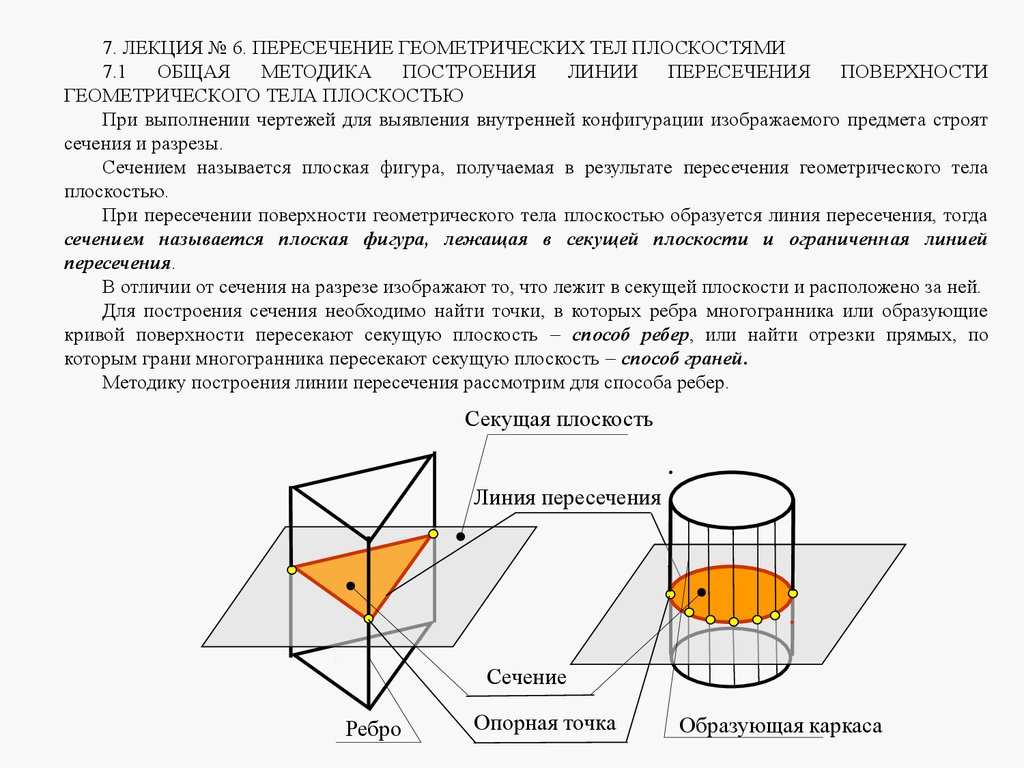
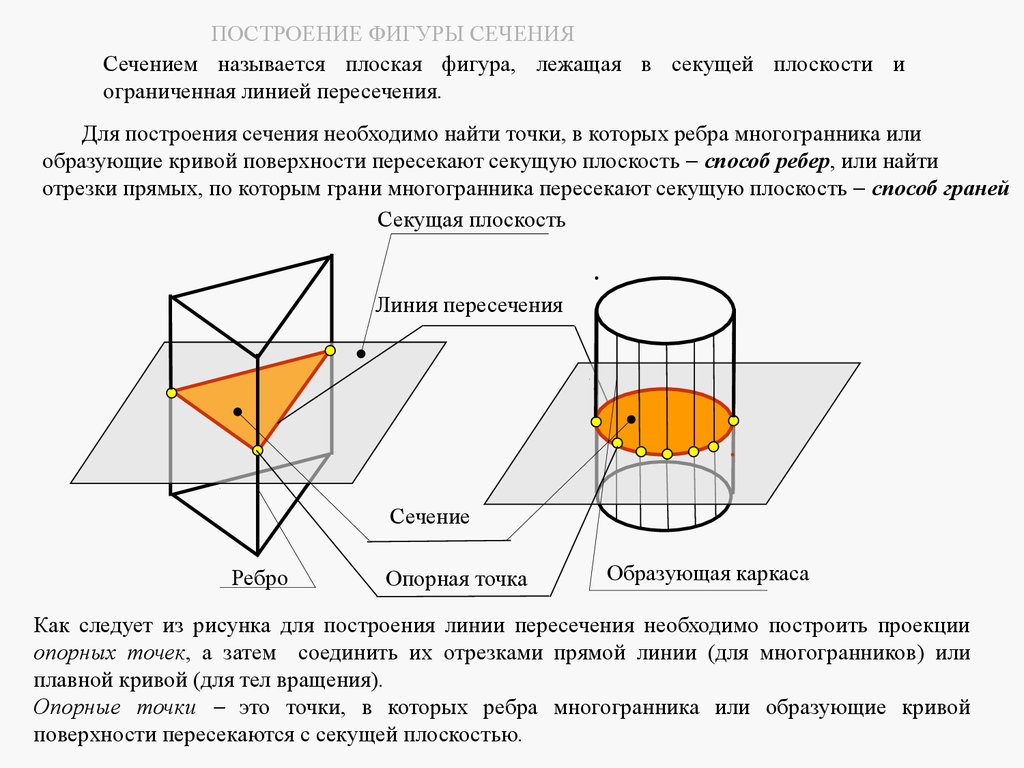
7 ЛЕКЦИЯ № 6. ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЛОСКОСТЯМИ
7.1 ОБЩАЯ МЕТОДИКА ПОСТРОЕНИЯ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТИ
ГЕОМЕТРИЧЕСКОГО ТЕЛА ПЛОСКОСТЬЮ
7.2 ПЕРЕСЕЧЕНИЕ МНОГОГРАННОЙ, ЦИЛИНДРИЧЕСКОЙ И КОНИЧЕСКОЙ
ПОВЕРХНОСТИ ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ И НАХОЖДЕНИЕ НАТУРАЛЬНОЙ
ВЕЛИЧИНЫ СЕЧЕНИЯ
4.
ПРЕДИСЛОВИЕЗнание инженерной графики позволяет специалисту выполнять и читать
чертежи и схемы так же, как знание азбуки и грамматики позволяет человеку читать и
писать тексты.
Условиями успешного овладения техническими знаниями является умение
читать чертежи и знание правил их выполнения и оформления.
На чертеже форму предмета передают, как правило, несколькими
изображениями. Каждое изображение дается только с одной стороны предмета. Чтобы
представить себе, рассматривая чертеж, форму предмета в целом, надо мысленно
объединить его отдельные изображения.
Уметь читать чертеж – это значит по изображениям предмета уметь представить
себе его пространственную форму. Инженерная графика формирует и развивает
пространственное мышление.
Инженерная графика является таким предметом, при изучении которого
обучаемые знакомятся с широким кругом технических понятий. Это поможет им
овладевать специальными учебными дисциплинами, расширит их технический
кругозор и позволит осознанно читать любую техническую литературу, содержащую
чертежи и схемы. Знание этой дисциплины в дальнейшем облегчает изучение
общеинженерных и специальных дисциплин.
Невозможно представить инженера, не знающего основ теории и практики
построения изображений.
5.
1 ОБОЗНАЧЕНИЯ ИСИМВОЛЫ
1.1 ОБОЗНАЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
, 1.1.1 Точка и прямая
А, В, С или 1, 2, 3 – точки, расположенные в пространстве (прописные буквы латинского
алфавита или арабские цифры);
А1, А2, А3 или 11, 12, 13 − последовательность точек;
а ,b, c ,d ,e ,g − прямые и кривые линии пространства (строчные буквы латинского алфавита)
h, ,f, p
– главные линии плоскости (горизонталь h, фронталь f, профильная прямая p);
(АВ)
[АВ]
|АВ|
А1, А2, А3
–
–
–
–
прямая, проходящая через точку А и В;
отрезок прямой, ограниченный точками А и В;
длина отрезка АВ или расстояние между точками А и В;
проекции точки А (горизонтальная А1, фронтальная А2, профильная А3);
– аксонометрическая проекция точки А;
– проекции линии (горизонтальная а1, фронтальная а2,
профильная а3);
À
а1, а2, а3
– аксонометрическая проекция прямой а;
à
[А1В1],[А2В2]
[А3В3]
M, N, P
x, y, z
x12 , y13 , z23
s14, s25, s45
x y z
i, j
– проекции отрезка прямой АВ (горизонтальная [А1В1],
фронтальная [А2В2], профильная [А3В3]);
– следы прямой (горизонтальный М, фронтальный N, профильный Р);
– оси проекций;
– оси проекций с добавлением индексов плоскостей проекций;
– новые оси проекций;
– аксонометрические оси проекций;
– оси вращения
6.
1.1.2 ПлоскостьП1, П2, П3 – плоскости проекций (горизонтальная П1, фронтальная П2,
профильная П3);
П4, П5
– новые плоскости проекций;
П΄
– плоскость аксонометрических проекций;
Г, Θ, Ρ, Σ, Τ – плоскости и поверхности (прописные буквы греческого
алфавита);
Θ (А, В, С) – плоскость Θ задана тремя точками А, В и С;
Р (а, А)
– плоскость Р задана прямой а и точкой А;
Σ (b∩с)
– плоскость Σ задана двумя пересекающимися прямыми b и с;
Т (d//е)
– плоскость Т задана двумя параллельными прямыми d и е;
Ф (∆ АВС) – плоскость Ф задана плоской фигурой – треугольником АВС;
РП , РП ,РП – следы плоскостей общего положения (горизонтальный РП1, фронтальный РП2,
1
2
Г1, Г2, Г3
3
профильный РП3);
– следы проецирующих плоскостей (горизонтальный Г 1, фрон тальный Г2, профильный Г3).
1.1.3 Угол
АВС
α, β, γ
∟
– угол с вершиной в точке В;
– углы наклона к плоскостям проекций (строчные буквы греческого алфавита);
угол наклона к горизонтальной плоскости проекций α ,к фронтальной β,
к профильной γ;
– прямой угол.
7.
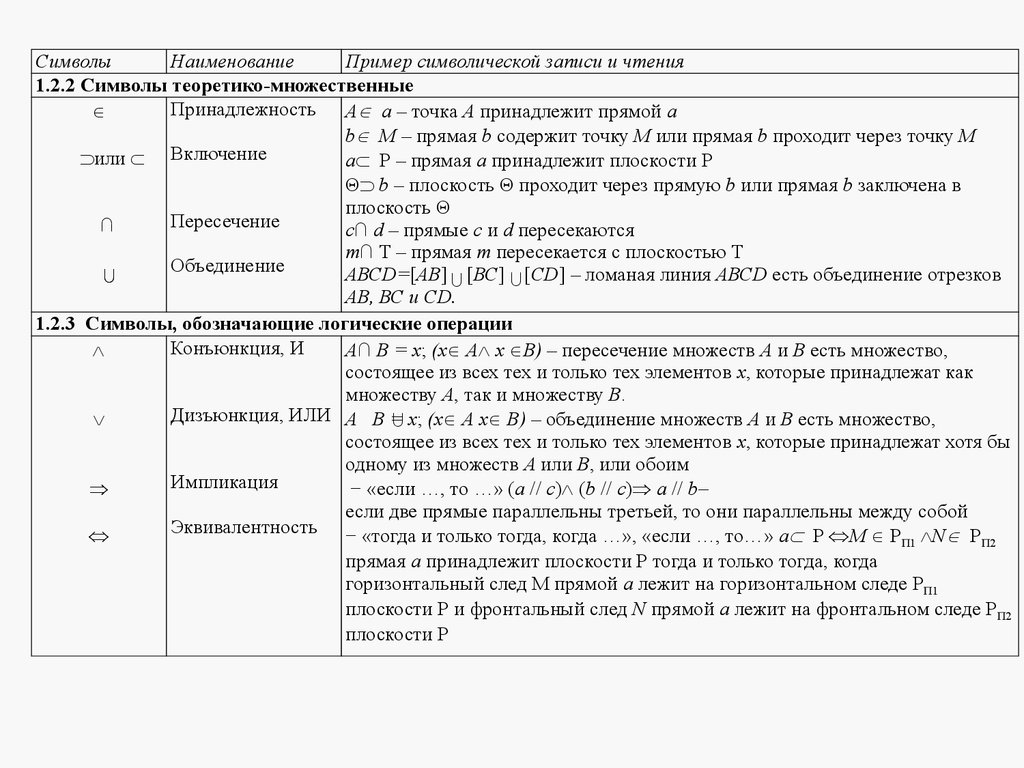
1.2 СИМВОЛЫСимволы
Наименование
Пример символической записи и чтения
1.2.1 Символы, выражающие отношение между геометрическими фигурами
=
≡
Результат
Совпадение
~
//
Подобны
Параллельны
Перпендикулярны
Скрещиваются
Отображение,
замена
Направление
проецирования
→
_
S
а ∩ Р = К – прямая а пересекает плоскость Р в точке К
(АВ) ≡ (СD) – прямая, проходящая через точки А и В,
совпадает с прямой, проходящей через точки С и D
М ≡ М1 – горизонтальный след М прямой совпадает со
своей горизонтальной проекцией М1
∆АВС ~ ∆МNК – треугольники АВС и МNК подобны
а//b – прямые а и b параллельны
с Σ – прямая с перпендикулярна плоскости Σ
а
b прямые а и b скрещиваются
П2 → П4 – плоскость проекций П2 заменена
плоскостью проекций П4
8.
СимволыНаименование
Пример символической записи и чтения
1.2.2 Символы теоретико-множественные
Принадлежность А а – точка А принадлежит прямой а
b М – прямая b содержит точку М или прямая b проходит через точку М
или Включение
а Р – прямая а принадлежит плоскости Р
Θ b – плоскость Θ проходит через прямую b или прямая b заключена в
плоскость Θ
Пересечение
∩
с∩ d – прямые с и d пересекаются
т∩ Т – прямая т пересекается с плоскостью Т
Объединение
АВСD=[АВ] [ВС] [CD] – ломаная линия АВСD есть объединение отрезков
АВ, ВС и СD.
1.2.3 Символы, обозначающие логические операции
Конъюнкция, И
А∩ В = х; (х А х В) – пересечение множеств А и В есть множество,
состоящее из всех тех и только тех элементов х, которые принадлежат как
множеству А, так и множеству В.
Дизъюнкция, ИЛИ А В = х; (х А х В) – объединение множеств А и В есть множество,
состоящее из всех тех и только тех элементов х, которые принадлежат хотя бы
одному из множеств А или В, или обоим
Импликация
− «если …, то …» (а // с) (b // c) а // b
если две прямые параллельны третьей, то они параллельны между собой
Эквивалентность
− «тогда и только тогда, когда …», «если …, то…» а Р М РП1 N РП2
прямая а принадлежит плоскости Р тогда и только тогда, когда
горизонтальный след М прямой а лежит на горизонтальном следе РП1
плоскости Р и фронтальный след N прямой а лежит на фронтальном следе РП2
плоскости Р
9.
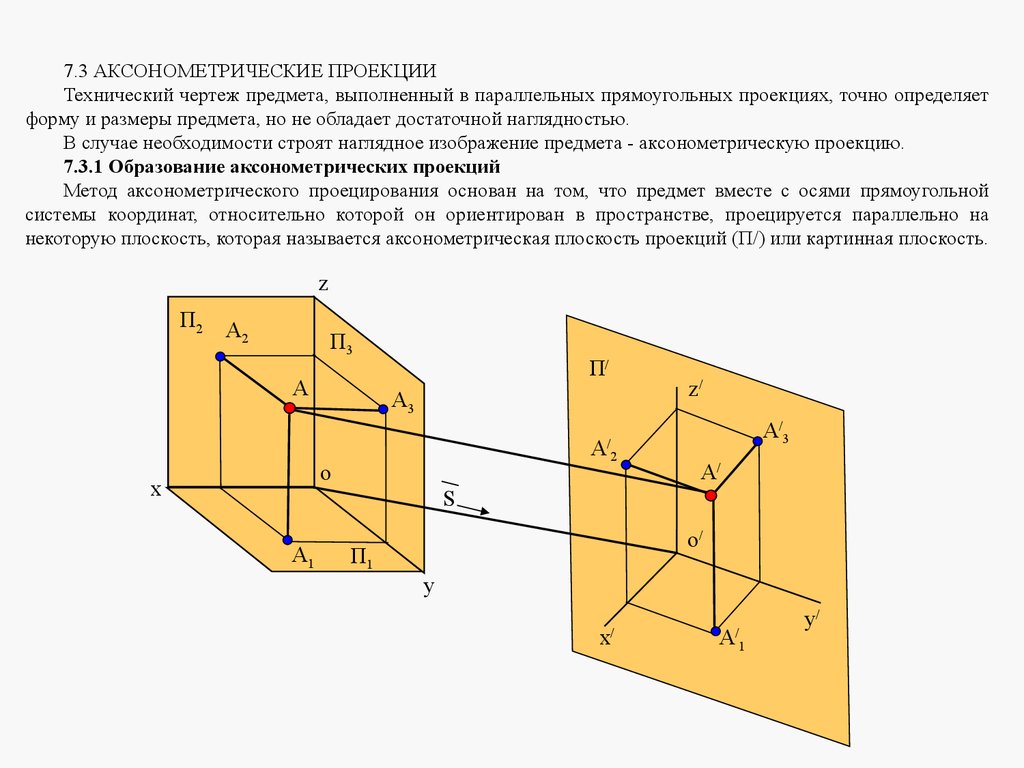
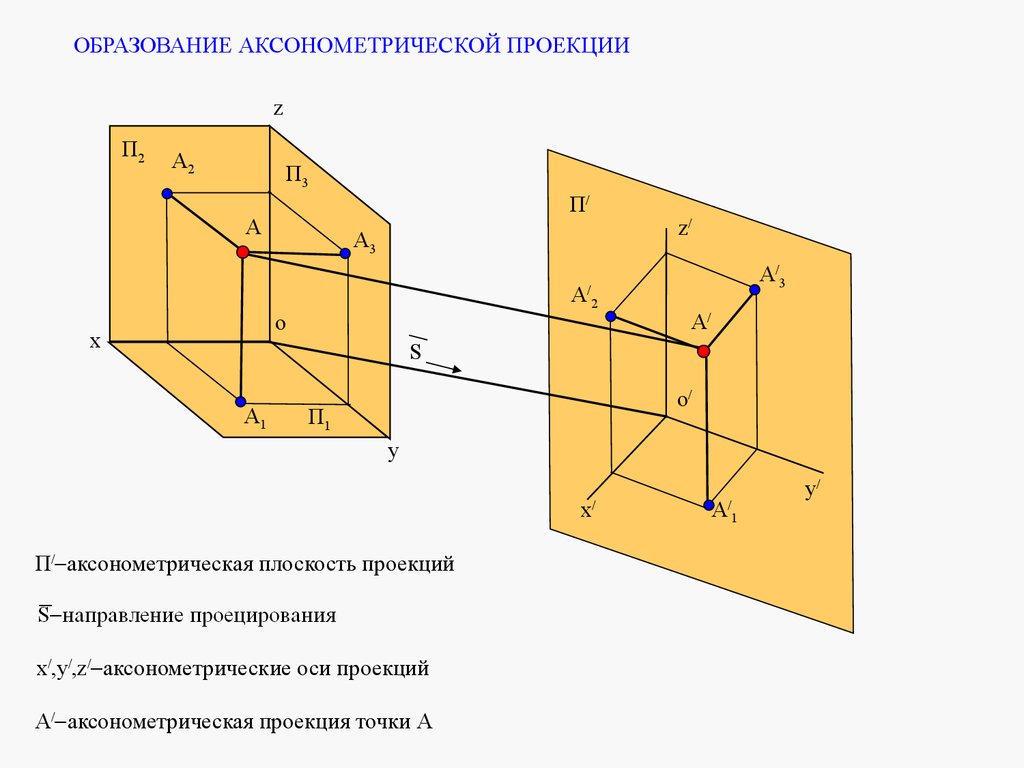
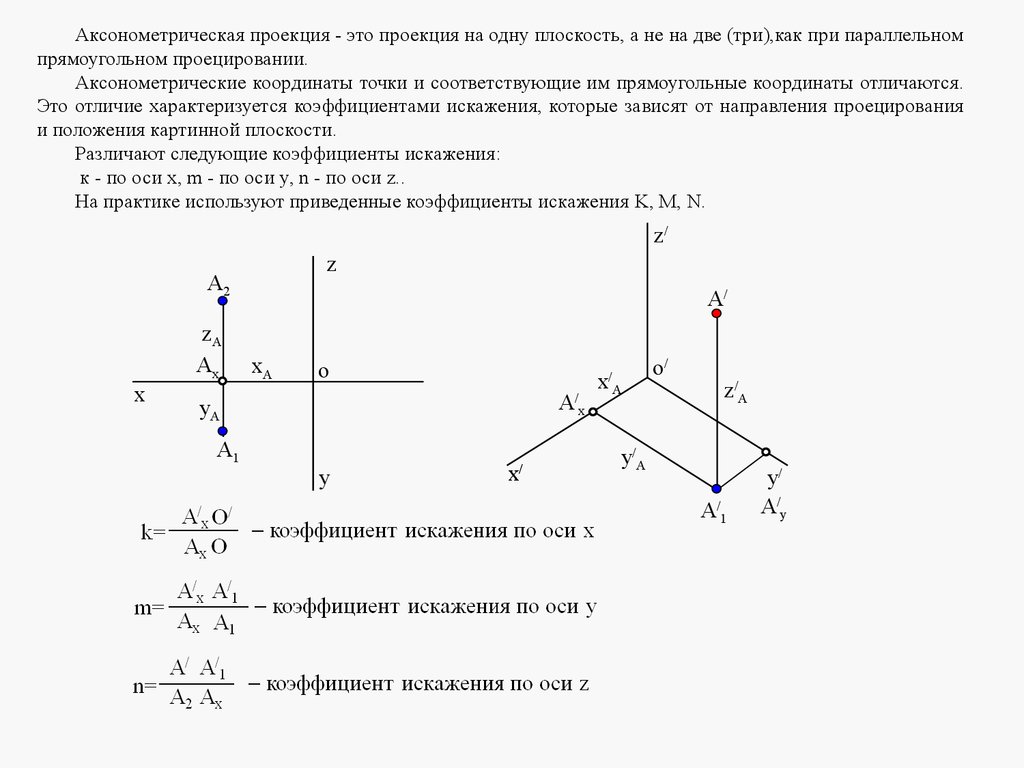
2. ЛЕКЦИЯ №1. ВВЕДЕНИЕ. ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ ЛИНИИОсновная цель учебной дисциплины «Инженерная графика» заключается в том, чтобы научиться
правильно, в соответствии с требованиями стандартов «Единой системы конструкторской документации»
(ЕСКД), изображать на чертежах и схемах различные изделия, читать чертежи и схемы, а также решать
различные геометрические задачи.
Изготовление различных предметов (изделий), строительство сооружений выполняется по чертежам.
Чертежом называется плоское изображение фигуры (предмета), выполненное в соответствии с
правилами начертательной геометрии.
Начертательная геометрия – это раздел геометрии, изучающий способы построения изображений
пространственных фигур на плоскости и алгоритмы решения метрических и позиционных задач по
заданным изображениям этих фигур.
Метрическими называют задачи по определению различных величин (расстояний, углов, длин
отрезков и т.д.).
Позиционными называют задачи по определению положения геометрической фигуры в
пространстве и взаимного положения геометрических фигур.
Важное прикладное значение начертательной геометрии состоит в том, что она учит грамотно
владеть выразительным техническим языком языком чертежа, создавать чертежи и свободно читать их.
10.
Выдающийся русский ученый профессор Курдюмов В.И.(1853 1904) дал следующее образное определениеначертательной геометрии: “Если чертеж является языком техники, одинаково понятным всем народам, то
начертательная геометрия служит грамматикой этого языка, т.е. она учит, как правильно читать чужие и
излагать наши собственные мысли, пользуясь в качестве слов одними только линиями и точками как
элементами всякого изображения”. Основателем начертательной геометрии считается французский ученый
Гаспар Монж (1746 1818).
Правила построения изображений, рассматриваемые в начертательной геометрии, основаны на
использовании метода проекций. Изучение метода проекций начинают с построения проекций точки и
отрезка прямой, которые являются простейшими элементами пространственных фигур.
2.1 МЕТОД ПАРАЛЛЕЛЬНОГО ПРЯМОУГОЛЬНОГО ПРОЕЦИРОВАНИЯ
Проецирование процесс получения изображения предмета на плоскости (от латинского слова proectio
бросание вперед, вдаль).
Плоскость, на которой получается изображение, называется плоскостью проекций, а полученное на ней
изображение проекцией.
Пусть имеется какая-то плоскость П1 и отрезок прямой АВ. Чтобы построить параллельную
прямоугольную проекцию отрезка прямой АВ на плоскость П 1, надо через его концевые точки А и В
провести параллельные прямые (проецирующие лучи) перпендикулярно плоскости П 1.Точки
пересечения проецирующих лучей с плоскостью П 1 (А1,В1) являются параллельными прямоугольными
проекциями точек А и В, а отрезок [A1B1] параллельная прямоугольная проекция отрезка AB.
Проецирующие лучи
А
S П1
В1
Плоскость проекций
Показать
В
А1
П1
[A1B1] П1
S - направление
проецирования
11.
[AB]-отрезок прямой, ограниченный концевыми точками А и ВПлоскость проекций плоскость, на которой получают
изображение
Проецирующие лучи
А
В
S П1
Плоскость проекций
В1
А1
П1
[A1B1] П1
S - направление
проецирования
Чтобы построить параллельную прямоугольную проекцию отрезка прямой АВ на плоскость
П1 надо через его концевые точки А и В провести параллельные прямые (проецирующие лучи)
перпендикулярно плоскости П1.
Точки пересечения проецирующих лучей с плоскостью П1 (А1,В1) являются
параллельными прямоугольными проекциями точек А и В, а отрезок [A1,B1]параллельная прямоугольная проекция отрезка АВ.
12.
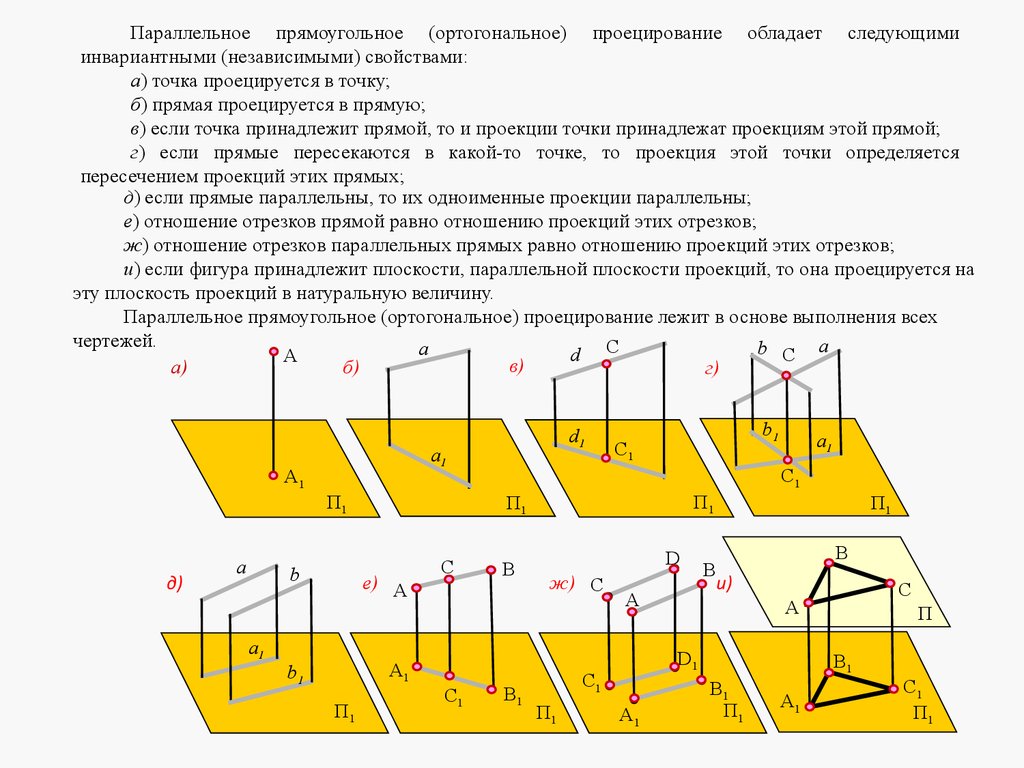
Параллельное прямоугольное (ортогональное) проецирование обладает следующимиинвариантными (независимыми) свойствами:
а) точка проецируется в точку;
б) прямая проецируется в прямую;
в) если точка принадлежит прямой, то и проекции точки принадлежат проекциям этой прямой;
г) если прямые пересекаются в какой-то точке, то проекция этой точки определяется
пересечением проекций этих прямых;
д) если прямые параллельны, то их одноименные проекции параллельны;
е) отношение отрезков прямой равно отношению проекций этих отрезков;
ж) отношение отрезков параллельных прямых равно отношению проекций этих отрезков;
и) если фигура принадлежит плоскости, параллельной плоскости проекций, то она проецируется на
эту плоскость проекций в натуральную величину.
Параллельное прямоугольное (ортогональное) проецирование лежит в основе выполнения всех
чертежей.
b С а
а
d С
А
в)
a)
б)
г)
а1
А1
П1
д)
а
b
а1
d1
С
А1
П1
С1
С1
а1
С1
П1
П1
е) А
b1
b1
В
В1
D
ж) С
А
В
В
и)
А1
С
А
D1
С1
П1
П1
П
В1
В1
П1
А1
С1
П1
13.
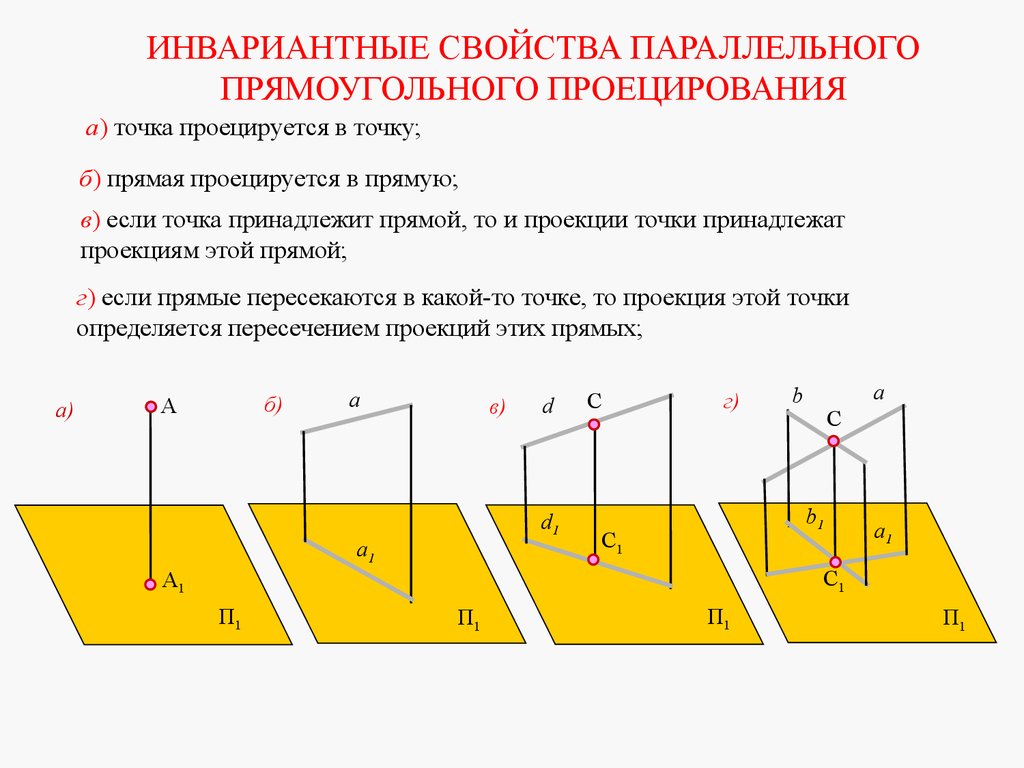
ИНВАРИАНТНЫЕ СВОЙСТВА ПАРАЛЛЕЛЬНОГОПРЯМОУГОЛЬНОГО ПРОЕЦИРОВАНИЯ
а) точка проецируется в точку;
б) прямая проецируется в прямую;
в) если точка принадлежит прямой, то и проекции точки принадлежат
проекциям этой прямой;
г) если прямые пересекаются в какой-то точке, то проекция этой точки
определяется пересечением проекций этих прямых;
a)
б)
А
а
в)
d
d1
а1
С
г)
а
b
С
b1
С1
а1
С1
А1
П1
П1
П1
П1
14.
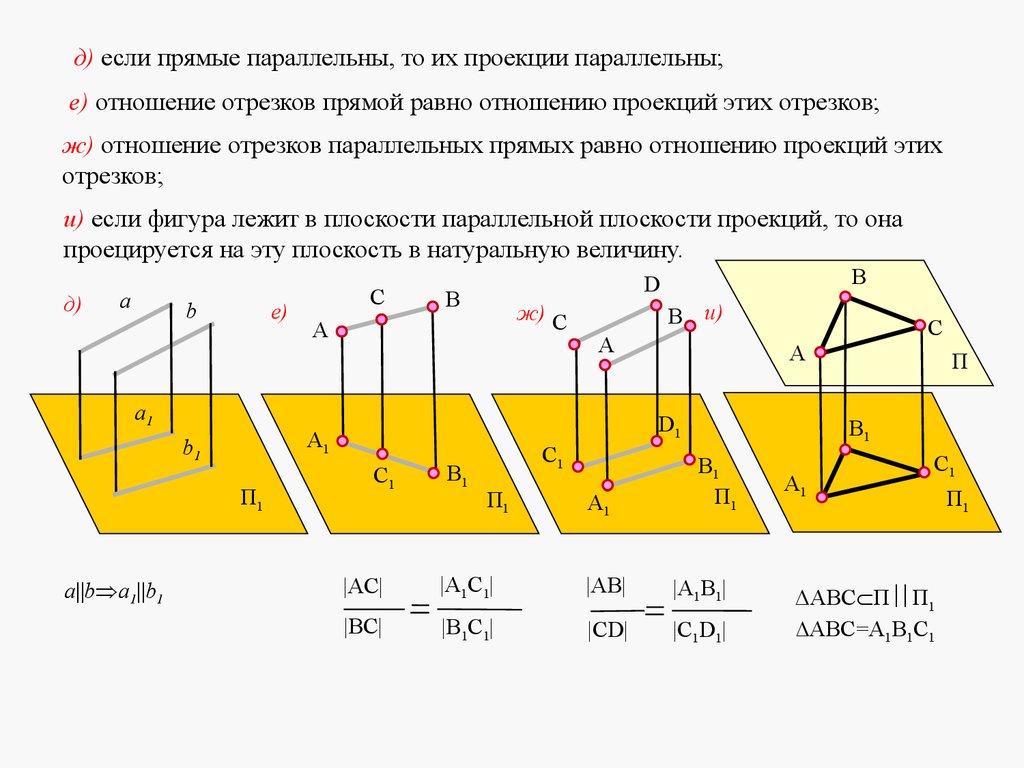
д) если прямые параллельны, то их проекции параллельны;е) отношение отрезков прямой равно отношению проекций этих отрезков;
ж) отношение отрезков параллельных прямых равно отношению проекций этих
отрезков;
и) если фигура лежит в плоскости параллельной плоскости проекций, то она
проецируется на эту плоскость в натуральную величину.
д)
а
b
е)
а1
В
ж) С
А
П1
В и)
А
С
А
D1
А1
b1
а b a1 b1
С
В
D
С1
В1
С1
П1
А1
П
В1
В1
П1
|АC|
|А1C1|
|АВ|
|А1В1|
|BC|
|B1C1|
|СD|
|С1D1|
А1
С1
ΔАВС П П1
∆АВС=А1В1С1
П1
15.
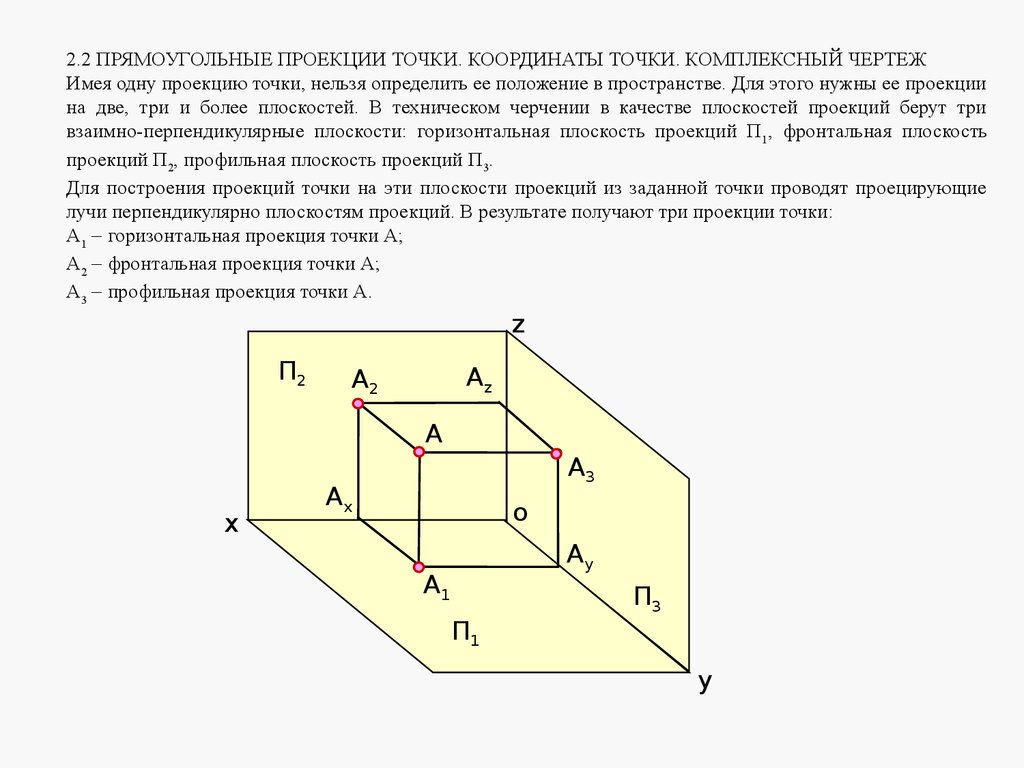
2.2 ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ. КООРДИНАТЫ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖИмея одну проекцию точки, нельзя определить ее положение в пространстве. Для этого нужны ее проекции
на две, три и более плоскостей. В техническом черчении в качестве плоскостей проекций берут три
взаимно-перпендикулярные плоскости: горизонтальная плоскость проекций П 1, фронтальная плоскость
проекций П2, профильная плоскость проекций П3.
Для построения проекций точки на эти плоскости проекций из заданной точки проводят проецирующие
лучи перпендикулярно плоскостям проекций. В результате получают три проекции точки:
А1 горизонтальная проекция точки А;
А2 фронтальная проекция точки А;
А3 профильная проекция точки А.
z
П2
Az
А2
A
x
А3
Ax
o
Ay
А1
П3
П1
y
16.
zП2
Az
А2
A
А3
x
Ax
o
Ay
А1
П3
П1
y
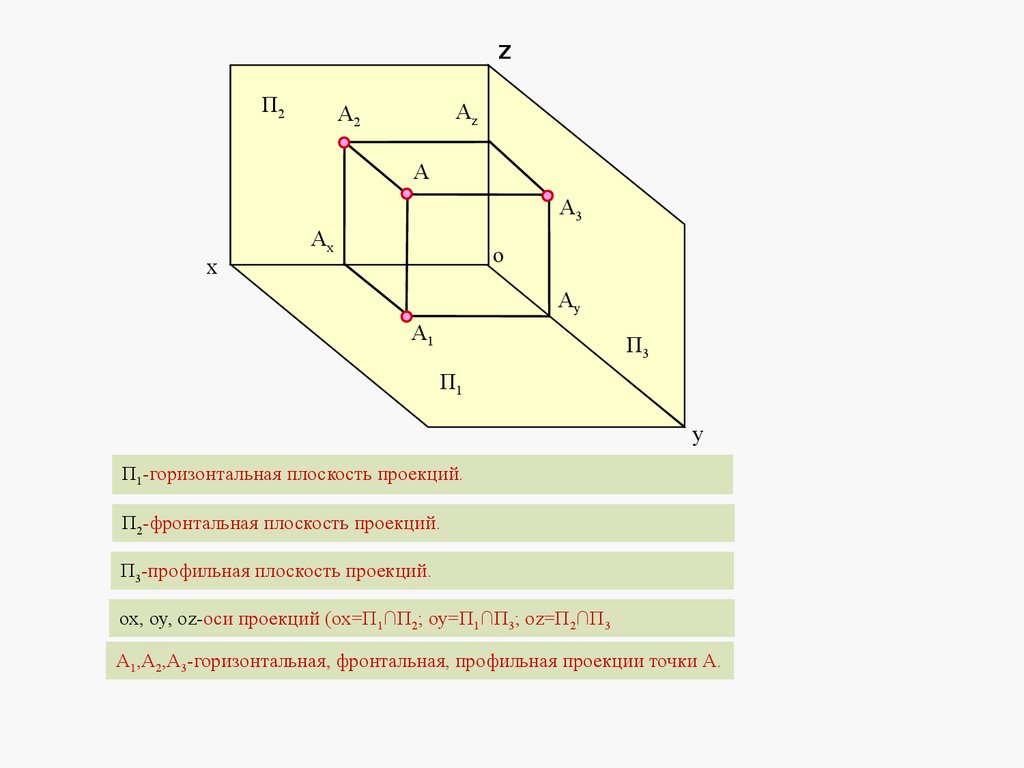
П1-горизонтальная плоскость проекций.
П2-фронтальная плоскость проекций.
П3-профильная плоскость проекций.
оx, оy, oz-оси проекций (ох=П1∩П2; oy=П1∩П3; oz=П2∩П3
А1,А2,А3-горизонтальная, фронтальная, профильная проекции точки А.
17.
Взаимно-перпендикулярные плоскости П1, П2, П3 называются координатными плоскостями, арасстояния между ними и заданной точкой координатами точек. Линии пересечения двух плоскостей
проекций образуют оси координат (ox,oy,oz). Начало координат точка пересечения трех плоскостей
проекций (о).
Показанное изображение проекций точки наглядно, но неудобно. В начертательной геометрии
проекции точки изображают в одной плоскости (плоскости листа). Для этого плоскость проекций П 1
поворачивают вокруг оси ox, а плоскость проекций П 3 вокруг оси oz до совмещения с плоскостью
проекций П2. В результате получают трехплоскостной чертеж, известный еще под названием эпюр (эпюр
Монжа, комплексный чертеж или просто чертеж).
П2
900
A
zz
А2
А3
A
А3
Ax
x
П3
o
А1
900
y
Ay
П3
П1
П1
А1
y
y
18.
zП2
900
Az
А2
А3
A
А3
Ax
x
П3
o
y
Ay
А1
900
П3
П1
П1
А1
y
y
П1-горизонтальная плоскость проекций.
П2-фронтальная плоскость проекций.
П3-профильная плоскость проекций.
оx, оy, oz-оси проекций (ох=П1∩П2; oy=П1∩П3; oz=П2∩П3
А1,А2,А3-горизонтальная, фронтальная, профильная проекции точки А.
19.
Вертикальная линиясвязи
Горизонтальная линия связи
П2
А2
z
Az
А3
П3
ZА
XА
Ax
x
o
Ay
y
YА
А1
П1
Ay
y
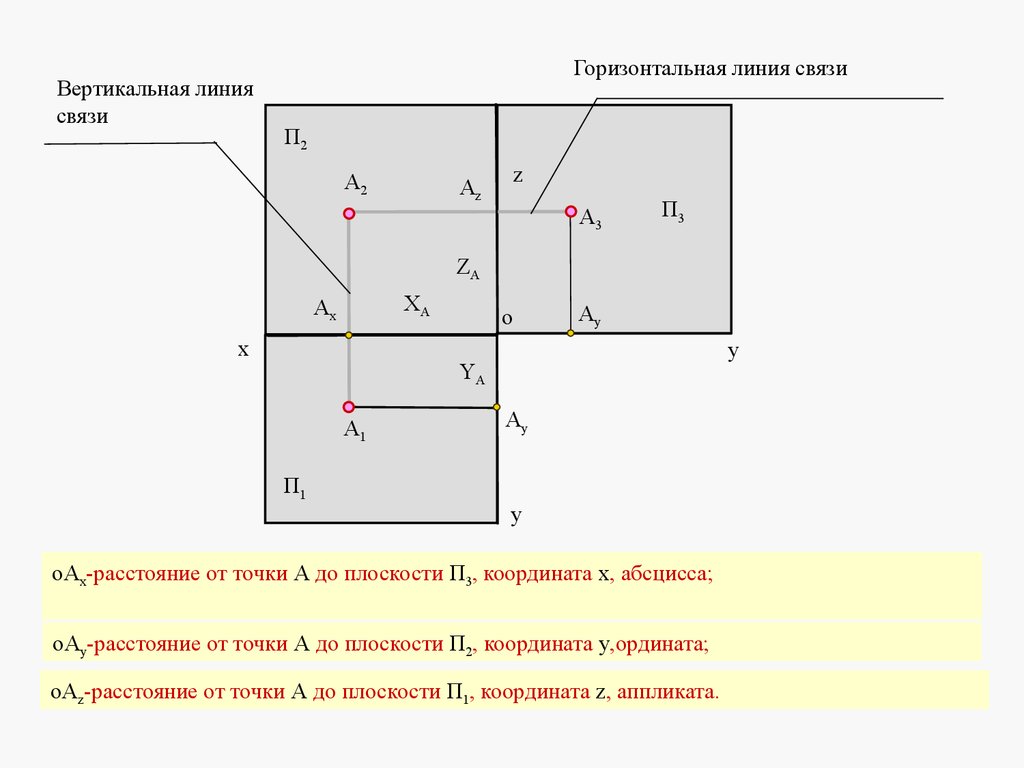
оАх-расстояние от точки А до плоскости П3, координата х, абсцисса;
оАy-расстояние от точки А до плоскости П2, координата y,ордината;
оАz-расстояние от точки А до плоскости П1, координата z, аппликата.
20.
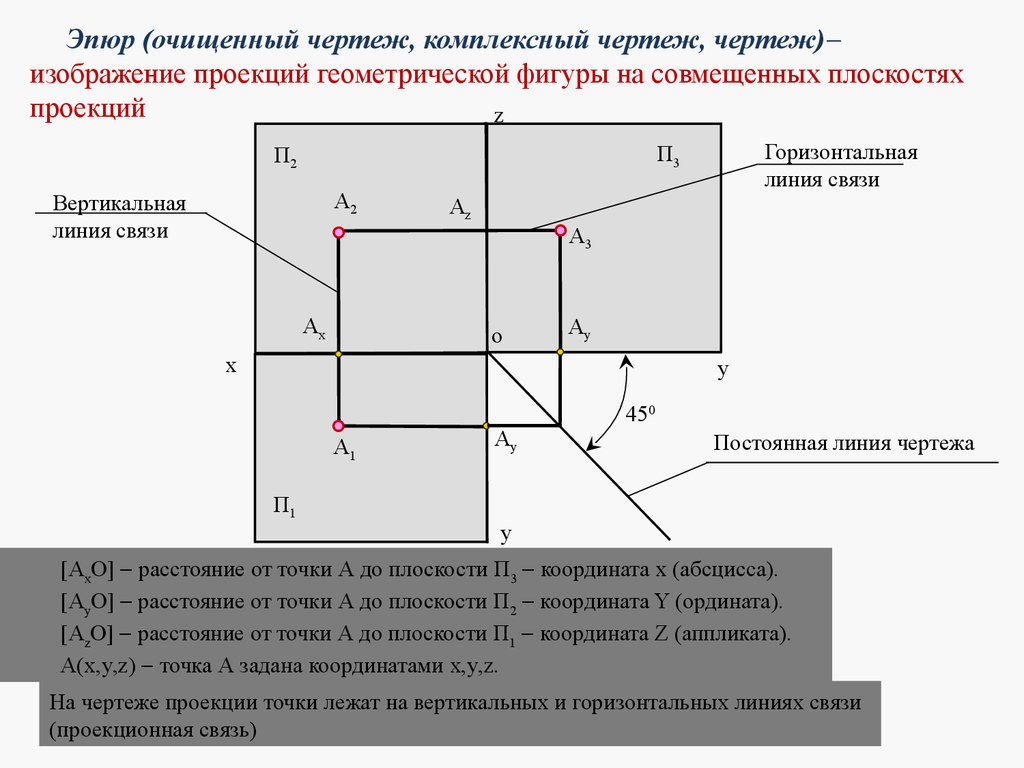
Эпюр (очищенный чертеж, комплексный чертеж, чертеж)изображение проекций геометрической фигуры на совмещенных плоскостях
проекций
z
Горизонтальная
линия связи
П3
П2
А2
Вертикальная
линия связи
Az
А3
Ax
o
Ay
x
y
А1
П1
Ay
450
Постоянная линия чертежа
y
[AxO] расстояние от точки А до плоскости П3 координата x (абсцисса).
[AyO] расстояние от точки А до плоскости П2 координата Y (ордината).
[AzO] расстояние от точки А до плоскости П1 координата Z (аппликата).
А(x,y,z) точка А задана координатами x,y,z.
На чертеже проекции точки лежат на вертикальных и горизонтальных линиях связи
(проекционная связь)
21.
2.3 ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙРанее мы установили, что для построения проекции отрезка прямой надо построить проекции его
концевых точек и соединить их.
В зависимости от положения отрезка прямой относительно плоскостей проекций различают
прямые общего и частного положения.
2.3.1 Прямые общего положения
Прямой общего положения называется прямая, не параллельная ни одной из плоскостей
проекций, а ее проекции не параллельны ни одной из осей проекций.
z
B2
П2
B2
В
В3
A2
A
z
В3
A3
A2
A3
x
x
A1
П1
В1
П3
y
A1
y
B1
y
22.
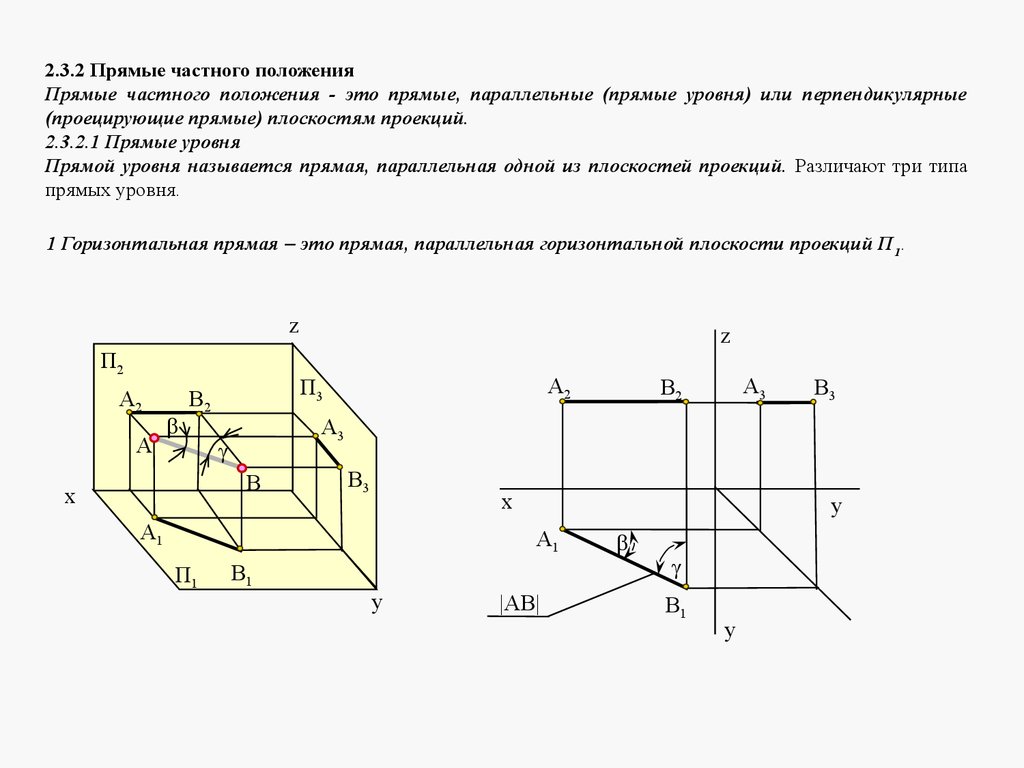
2.3.2 Прямые частного положенияПрямые частного положения - это прямые, параллельные (прямые уровня) или перпендикулярные
(проецирующие прямые) плоскостям проекций.
2.3.2.1 Прямые уровня
Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Различают три типа
прямых уровня.
1 Горизонтальная прямая это прямая, параллельная горизонтальной плоскости проекций П 1.
z
П2
A2
A
A2
П3
B2
В3
x
A1
B3
y
A1
П1
A3
B2
A3
В
x
z
В1
y
|AB|
B1
y
23.
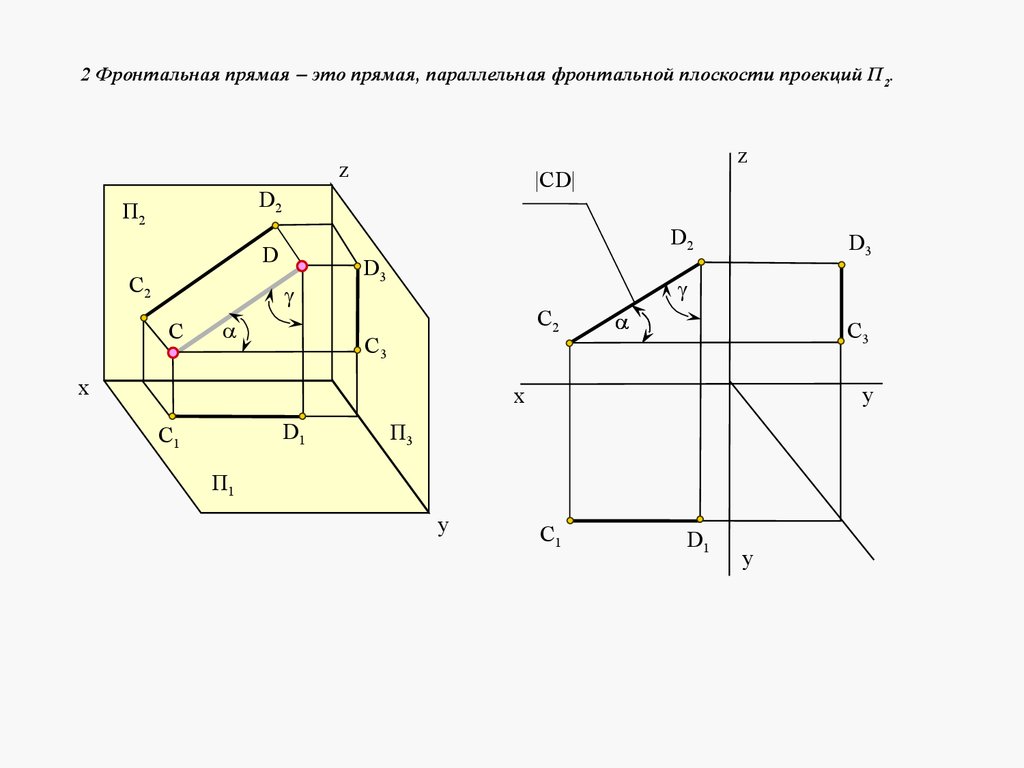
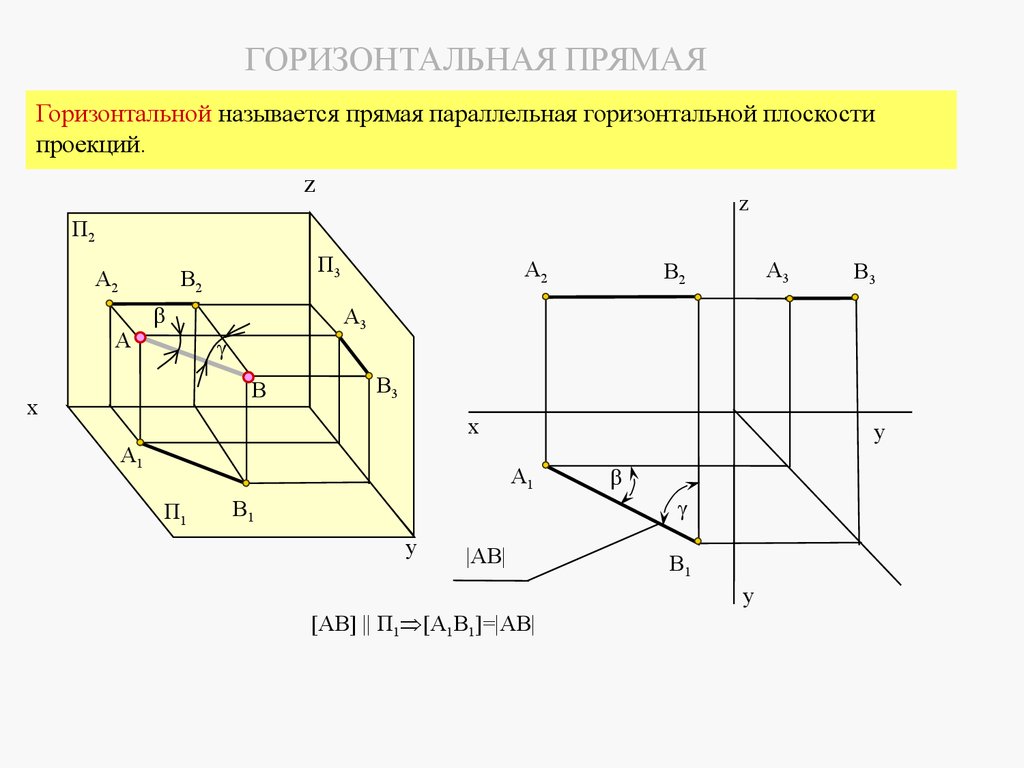
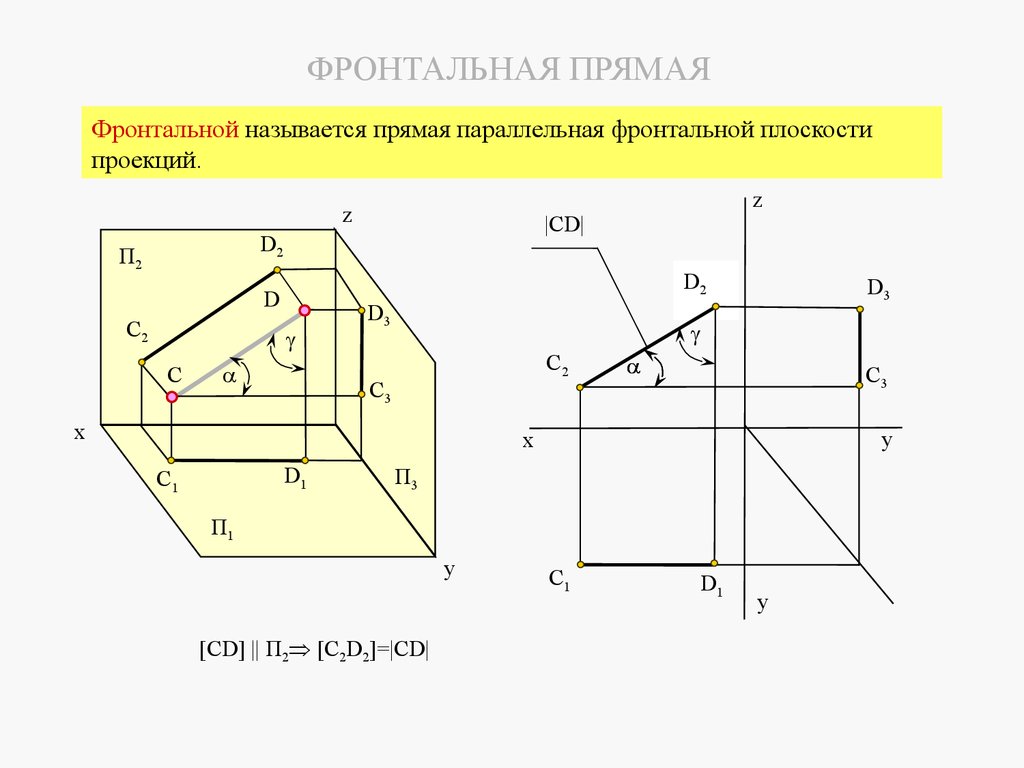
2 Фронтальная прямая это прямая, параллельная фронтальной плоскости проекций П 2.z
|CD|
D2
П2
D2
D
С2
С
z
D3
D3
C2
С3
x
C3
y
x
D1
С1
П3
П1
y
C1
D1
y
24.
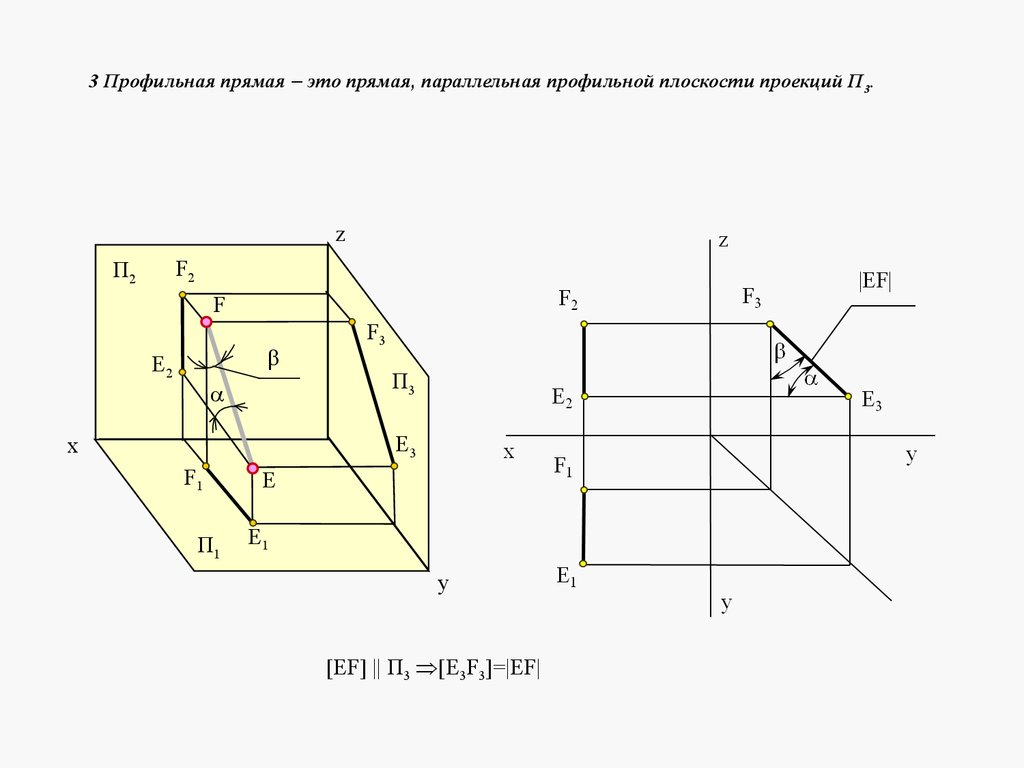
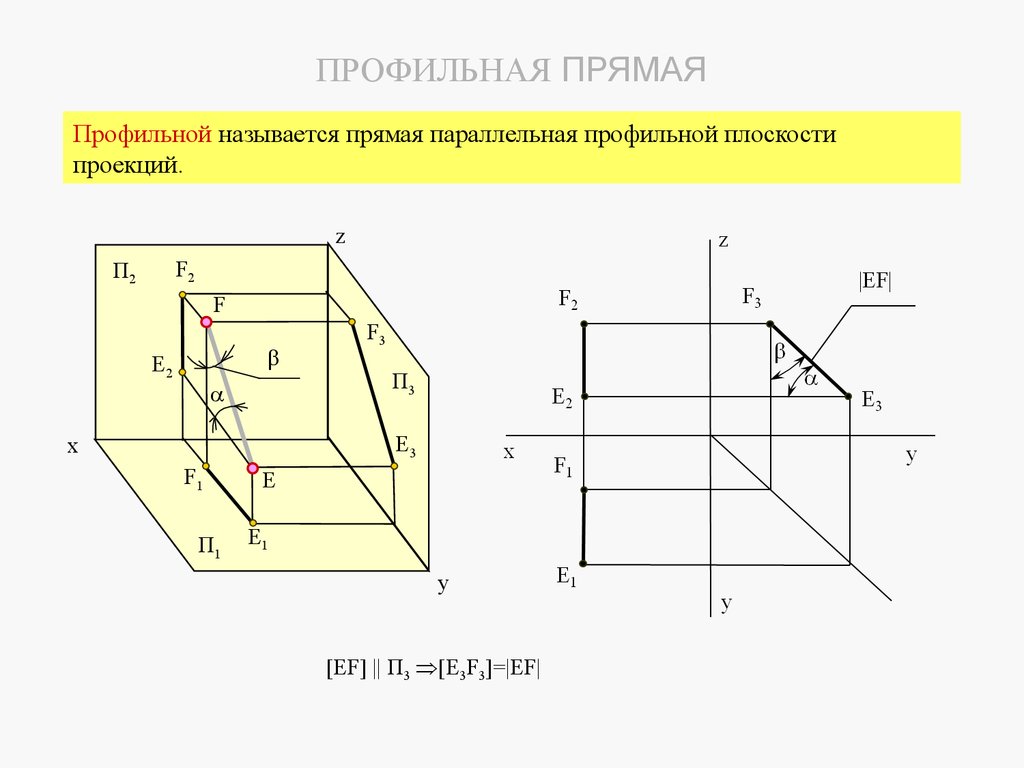
3 Профильная прямая это прямая, параллельная профильной плоскости проекций П 3.z
F2
П2
F
E2
F3
П3
E3
x
F1
П1
E
E1
y
[EF] || П3 [E3F3]=|EF|
25.
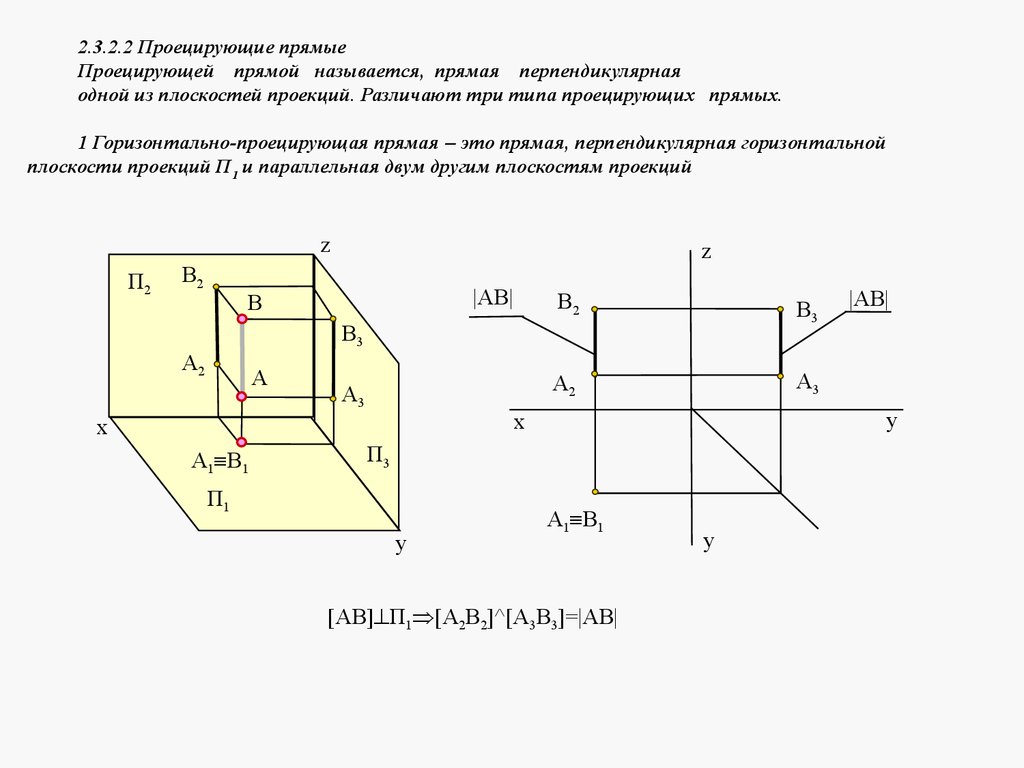
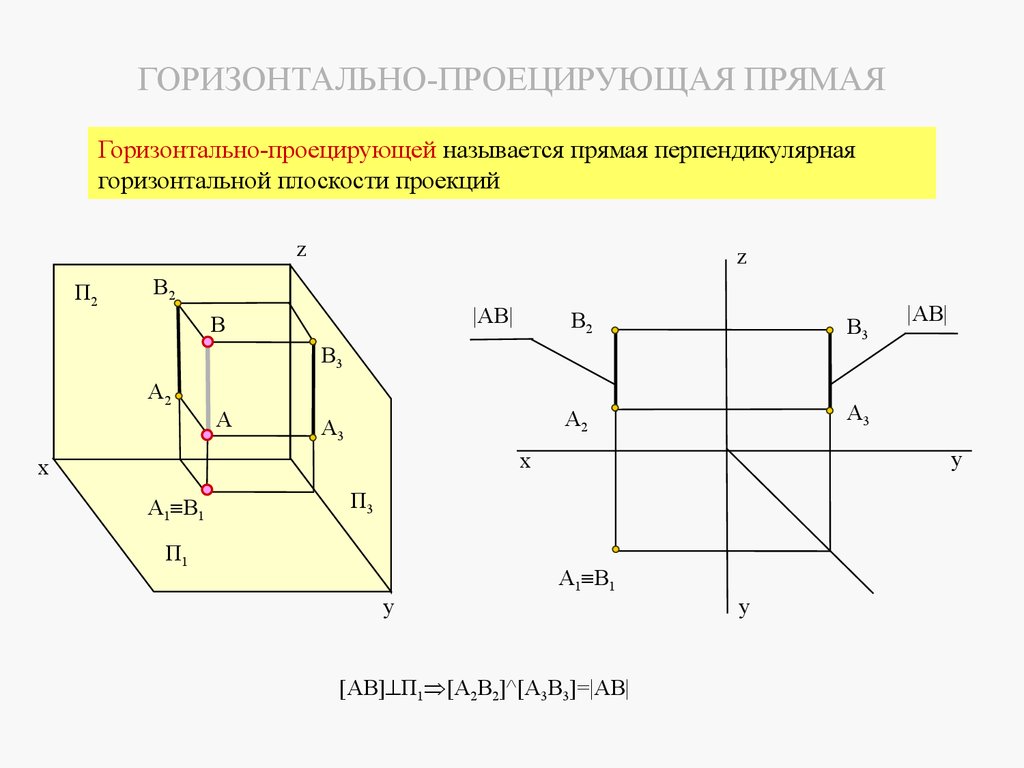
2.3.2.2 Проецирующие прямыеПроецирующей прямой называется, прямая перпендикулярная
одной из плоскостей проекций. Различают три типа проецирующих прямых.
1 Горизонтально-проецирующая прямая это прямая, перпендикулярная горизонтальной
плоскости проекций П1 и параллельная двум другим плоскостям проекций
z
П2
B2
z
|AB|
В
B2
B3
A2
A3
В3
A2
A
A3
A1 В1
y
x
x
П3
П1
y
|AB|
A1 В1
[AB] П1 [A2B2]^[A3B3]=|AB|
y
26.
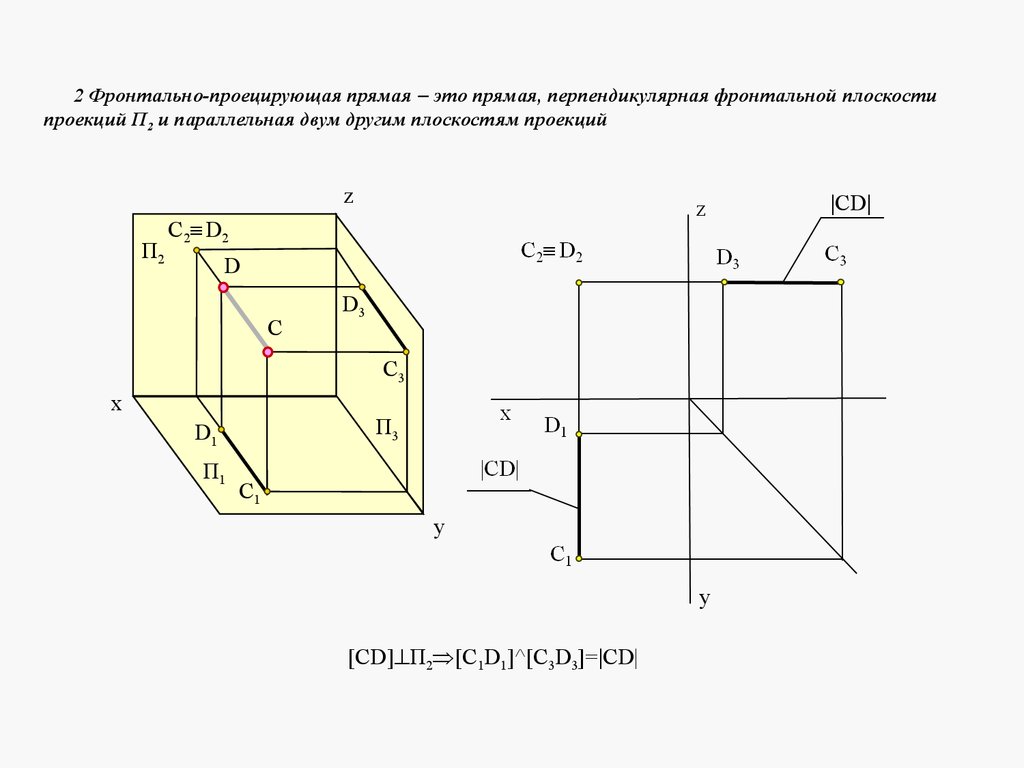
2 Фронтально-проецирующая прямая это прямая, перпендикулярная фронтальной плоскостипроекций П2 и параллельная двум другим плоскостям проекций
z
П2
СD
C2 D2
D
C
D3
С3
x
П3
D1
П1
C1
y
y
[CD] П2 [C1D1]^[C3D3]= CD|
27.
3 Профильно-проецирующая прямая это прямая, перпендикулярная профильной плоскостипроекций П3 и параллельная двум другим плоскостям проекций.
z
П2
z
П3
E2
E2
E3 F3
F2
F2
E
F
E3 F3
|AB|
x
x
E1
П1
y
F1
y
E1
F1
y
[EF] П3 [E1F1]^[E2F2]=|EF|
28.
ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯПрямой общего положения называется прямая не параллельная ни одной
плоскости проекций, а ее проекции не параллельны ни одной оси проекций.
z
B2
П2
B2
В
В3
A2
A
z
В3
A3
A2
A3
x
x
A1
П1
В1
П3
y
A1
y
B1
y
29.
ГОРИЗОНТАЛЬНАЯ ПРЯМАЯГоризонтальной называется прямая параллельная горизонтальной плоскости
проекций.
z
z
П2
A2
П3
B2
A
A3
B2
В
В3
x
A1
y
A1
П1
B3
A3
x
A2
В1
y
|AB|
[AB] || П1 [A1B1]=|AB|
B1
y
30. ФРОНТАЛЬНАЯ ПРЯМАЯ
Фронтальной называется прямая параллельная фронтальной плоскостипроекций.
z
|CD|
D2
П2
D2
D
С2
С
z
D3
D3
C2
С3
x
C3
y
x
D1
С1
П3
П1
y
[CD] || П2 [C2D2]=|CD|
C1
D1
y
31.
ПРОФИЛЬНАЯ ПРЯМАЯПрофильной называется прямая параллельная профильной плоскости
проекций.
z
F2
П2
F
E2
F3
П3
E3
x
F1
П1
E
E1
y
[EF] || П3 [E3F3]=|EF|
32.
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯГоризонтально-проецирующей называется прямая перпендикулярная
горизонтальной плоскости проекций
z
П2
z
B2
|AB|
В
B2
B3
A2
A3
В3
A2
A
A3
y
x
x
A1 В1
П3
П1
y
|AB|
A1 В1
[AB] П1 [A2B2]^[A3B3]=|AB|
y
33.
ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯФронтально-проецирующей называется прямая перпендикулярная
фронтальной плоскости проекций
z
П2
СD
C2 D2
D
C
D3
С3
x
П1
y
П3
D1
C1
y
y
[CD] П2 [C1D1]^[C3D3]= CD|
34.
ПРОФИЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯПрофильно-проецирующей называется прямая перпендикулярная профильной
плоскости проекций
z
П2
z
П3
E2
E2
F2
E3 F3
F2
E
F
E3 F3
|AB|
x
x
E1
П1
y
F1
y
E1
F1
y
[EF] П3 [E1F1]^[E2F2]=|EF|
35.
3. Лекция №2. ЧТЕНИЕ ЧЕРТЕЖА. МЕТРИЧЕСКИЕ И ПОЗИЦИОННЫЕ ЗАДАЧИ .ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
3.1 ЧТЕНИЕ ЧЕРТЕЖА
Под чтением чертежа понимают извлечение полезной информации о форме, размерах и положении в
пространстве предмета по заданным его проекциям. Например, на чертеже задан отрезок прямой АВ своими
проекциями. Из рассмотрения проекций видно, что фронтальная проекция параллельна оси х, следовательно,
прямая АВ это прямая, параллельная плоскости П1, и горизонтальная ее проекция А1В1 по длине равна
натуральной величине отрезка прямой АВ. Угол угол наклона прямой АВ к плоскости П2.
В результате чтения чертежа получена информация о размерах и положении в пространстве прямой АВ.
А2
x
В2
[AB] П1
А1
|АВ|
[А1В1] = АВ
В1
36.
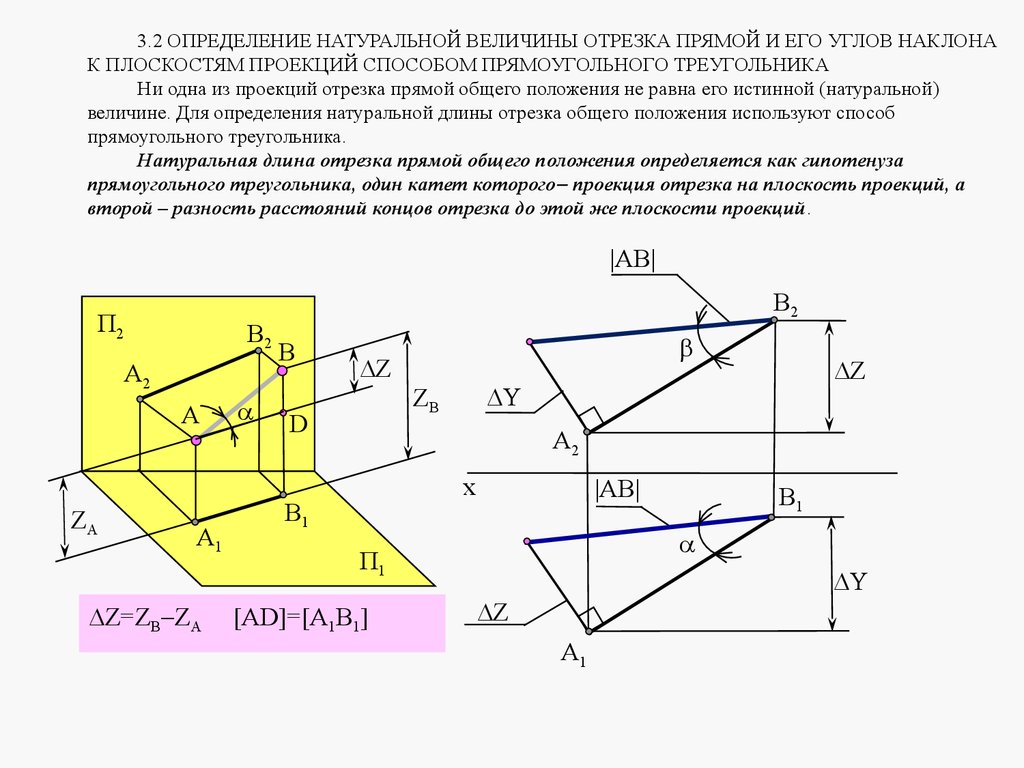
3.2 ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ И ЕГО УГЛОВ НАКЛОНАК ПЛОСКОСТЯМ ПРОЕКЦИЙ СПОСОБОМ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
Ни одна из проекций отрезка прямой общего положения не равна его истинной (натуральной)
величине. Для определения натуральной длины отрезка общего положения используют способ
прямоугольного треугольника.
Натуральная длина отрезка прямой общего положения определяется как гипотенуза
прямоугольного треугольника, один катет которого проекция отрезка на плоскость проекций, а
второй – разность расстояний концов отрезка до этой же плоскости проекций.
|AB|
П2
B2
A2
A
ZА
A1
Z=ZB ZA
B2
B
Z
Y
ZВ
D
Z
A2
х
B1
|AB|
П1
[AD]=[A1B1]
B1
Y
Z
A1
37.
СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА|AB|
B2
П2
B2
A2
A
ZА
Z=ZB ZA
A1
B
Z
Y
ZВ
D
A2
х
B1
[AD]=[A1B1]
Z
|AB|
B1
П1
Y
Z
A1
Натуральная длина отрезка прямой общего положения определяется как
гипотенуза прямоугольного треугольника, один катет которого проекция отрезка
на плоскость проекций, а второй – разность расстояний концов отрезка до этой же
плоскости проекций.
38.
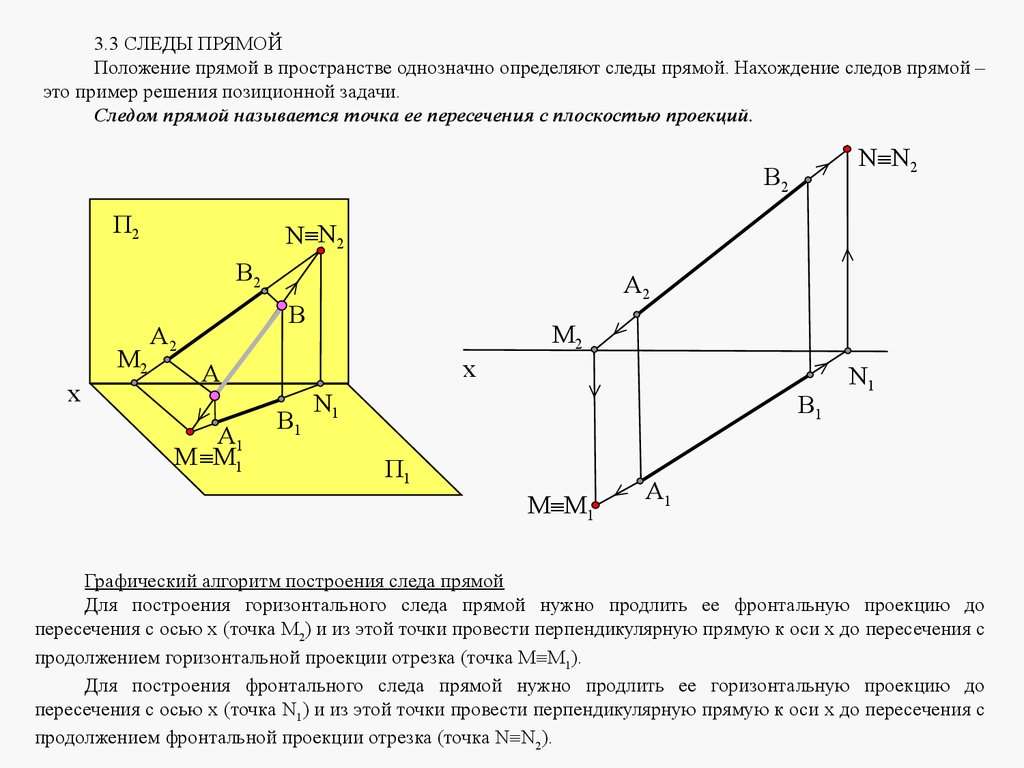
3.3 СЛЕДЫ ПРЯМОЙПоложение прямой в пространстве однозначно определяют следы прямой. Нахождение следов прямой –
это пример решения позиционной задачи.
Следом прямой называется точка ее пересечения с плоскостью проекций.
N N2
B2
П2
N N2
B2
M2
x
A2
B
A2
M2
x
A
А1
M M1
B1
N1
B1
П1
M M1
N1
A1
Графический алгоритм построения следа прямой
Для построения горизонтального следа прямой нужно продлить ее фронтальную проекцию до
пересечения с осью х (точка М2) и из этой точки провести перпендикулярную прямую к оси х до пересечения с
продолжением горизонтальной проекции отрезка (точка М М1).
Для построения фронтального следа прямой нужно продлить ее горизонтальную проекцию до
пересечения с осью х (точка N1) и из этой точки провести перпендикулярную прямую к оси х до пересечения с
продолжением фронтальной проекции отрезка (точка N N2).
39.
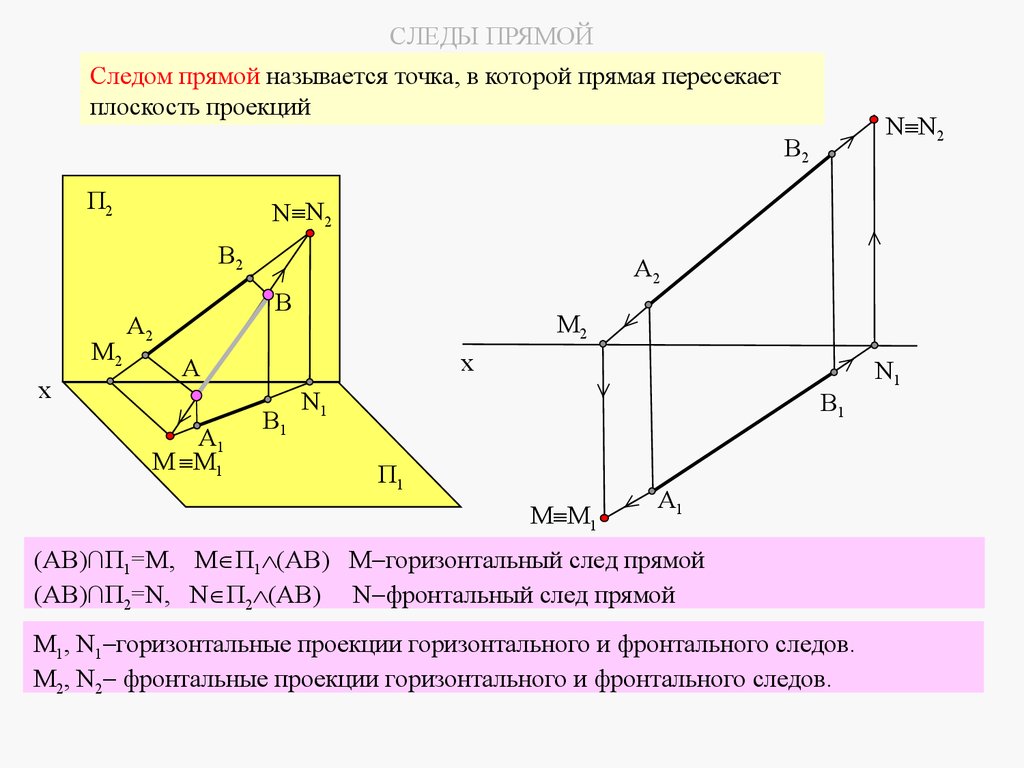
СЛЕДЫ ПРЯМОЙСледом прямой называется точка, в которой прямая пересекает
плоскость проекций
N N2
B2
П2
N N2
B2
M2
x
A2
B
A2
M2
x
A
А1
M M1
B1
N1
B1
П1
M M1
A1
(AB)∩П1=М, М П1 (АВ) М горизонтальный след прямой
(АВ)∩П2=N, N П2 (АВ) N фронтальный след прямой
М1, N1 горизонтальные проекции горизонтального и фронтального следов.
M2, N2 фронтальные проекции горизонтального и фронтального следов.
N1
40.
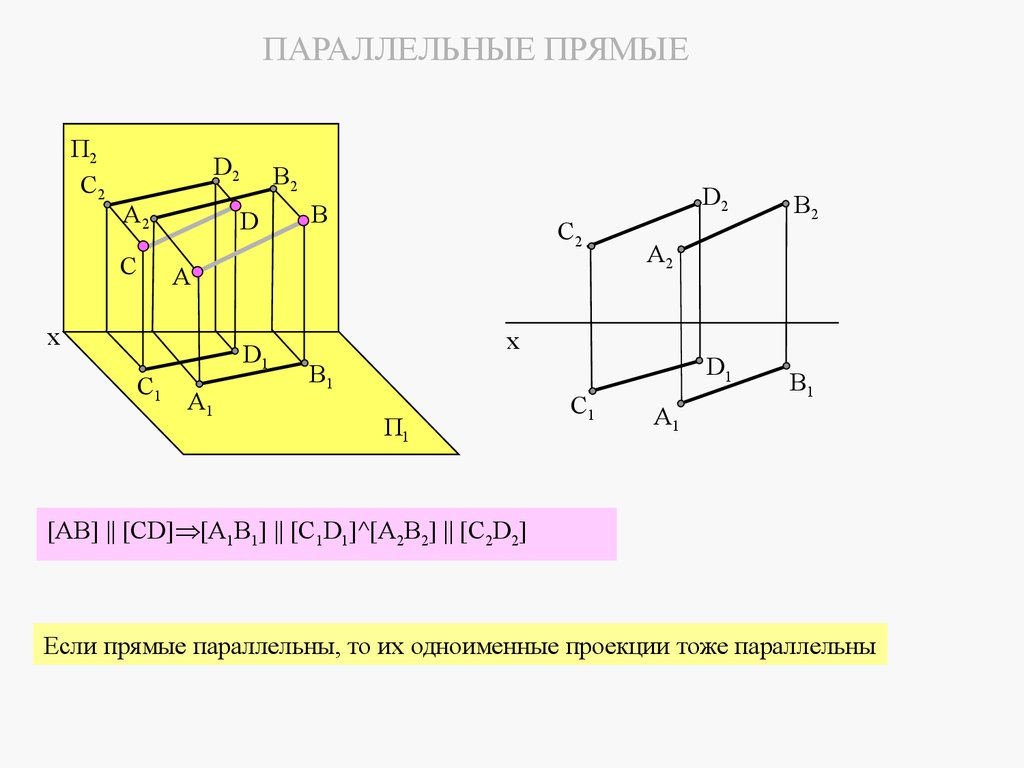
3.4 ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХДве прямые в пространстве могут быть параллельными, пересекаться и скрещиваться.
3.4.1 Параллельные прямые
Если две прямые параллельны, то их одноименные проекции тоже параллельны.
B2
x
A2
C2
A1
C1
B1
D2
D1
[AB] || [CD] [A1B1] || [C1D1] [A2B2] || [C2D2]
41.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕП2
C2
D2
A2
C
D
D2
B
C2
A
x
C1
B2
D1
A1
A2
x
B1
П1
D1
C1
B2
B1
A1
[AB] || [CD] [A1B1] || [C1D1]^[A2B2] || [C2D2]
Если прямые параллельны, то их одноименные проекции тоже параллельны
42.
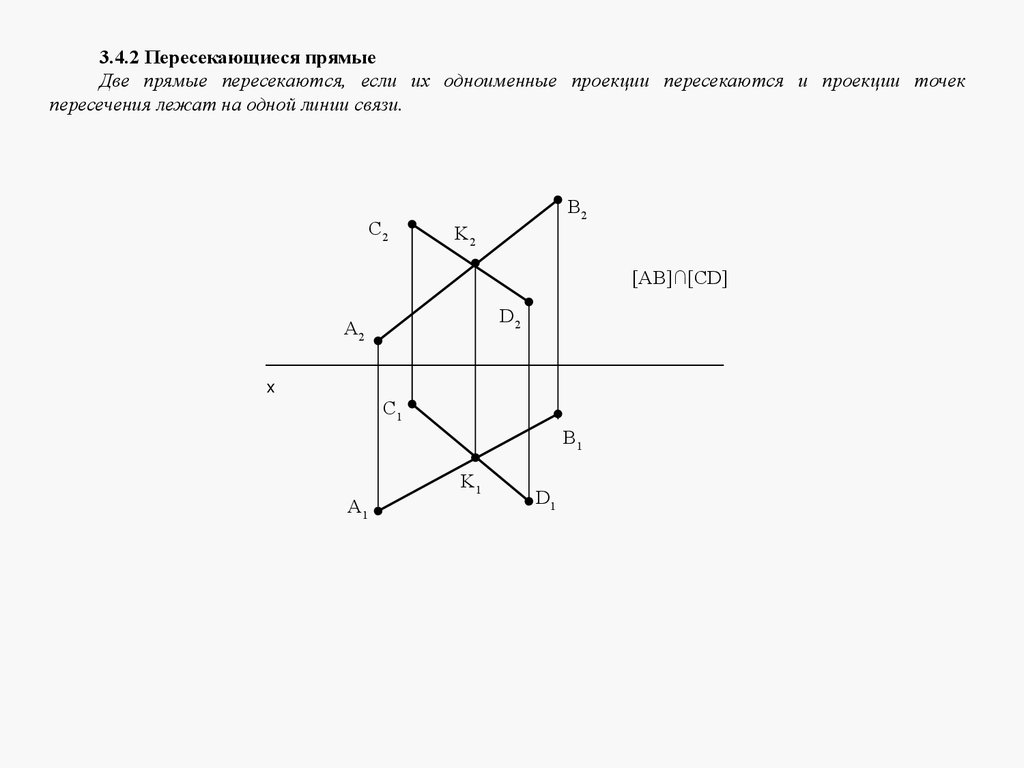
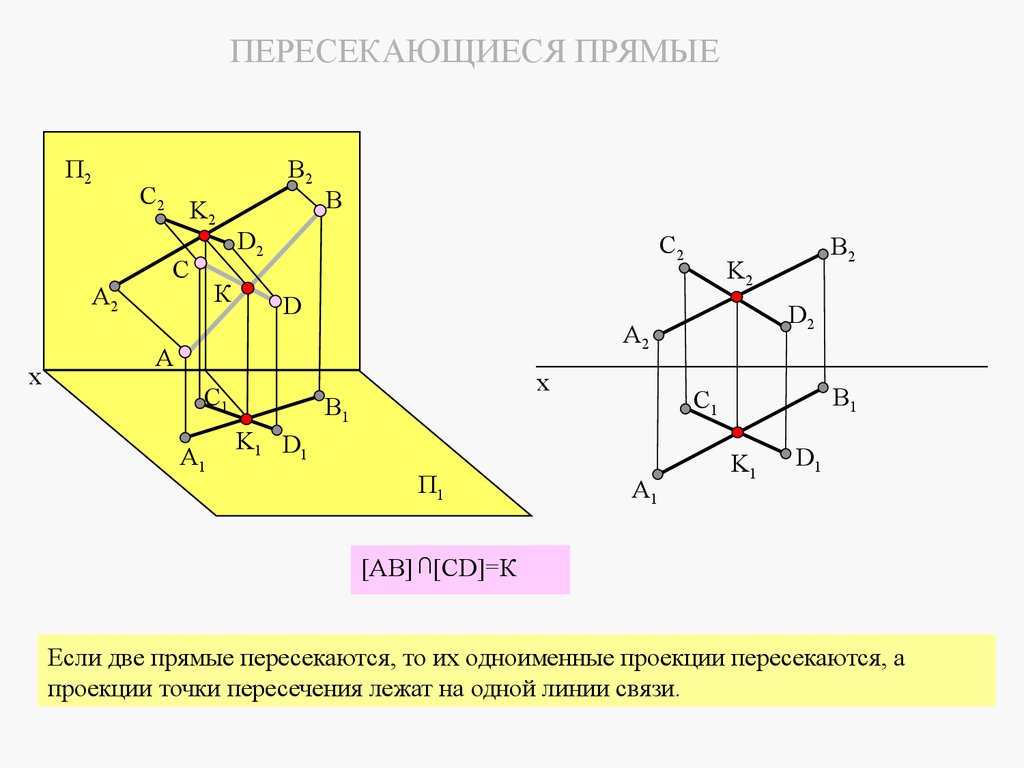
3.4.2 Пересекающиеся прямыеДве прямые пересекаются, если их одноименные проекции пересекаются и проекции точек
пересечения лежат на одной линии связи.
C2
B2
K2
[AB]∩[CD]
D2
A2
x
C1
B1
A1
K1
D1
43.
ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕП2
C2
A2
K2
C
К
B
D2
C2
K2
D
D2
A2
A
C1
A1
x
B1
B1
C1
K1 D1
П1
B2
A1
K1
D1
[AB] [CD]=К
x
B2
Если две прямые пересекаются, то их одноименные проекции пересекаются, а
проекции точки пересечения лежат на одной линии связи.
44.
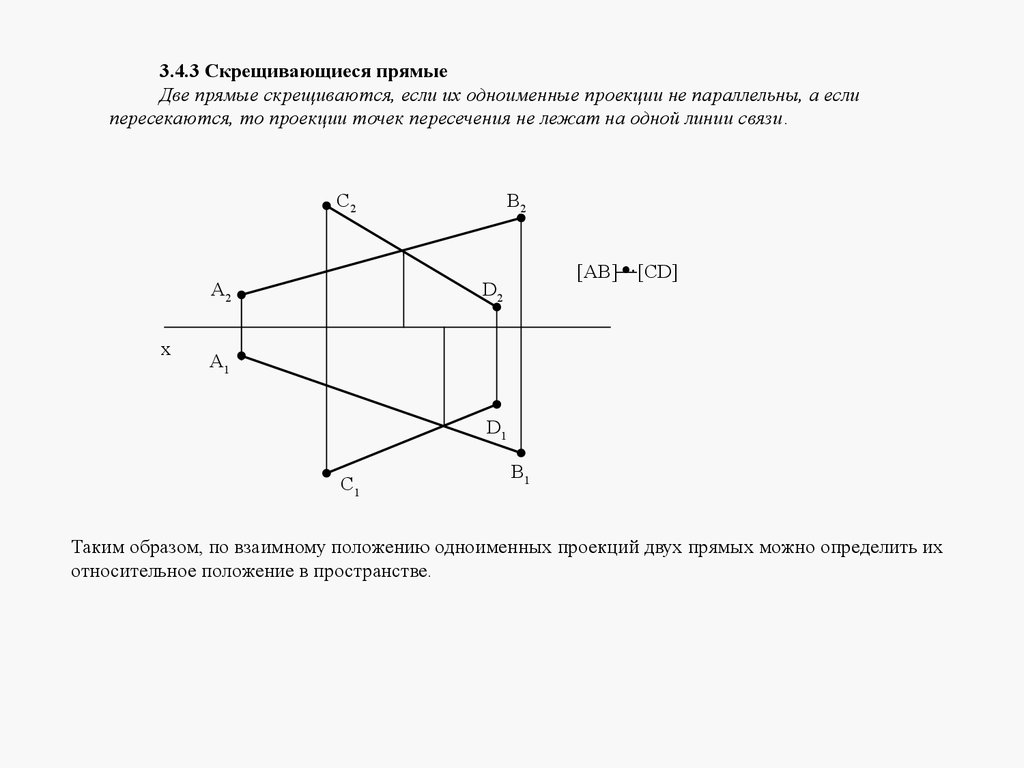
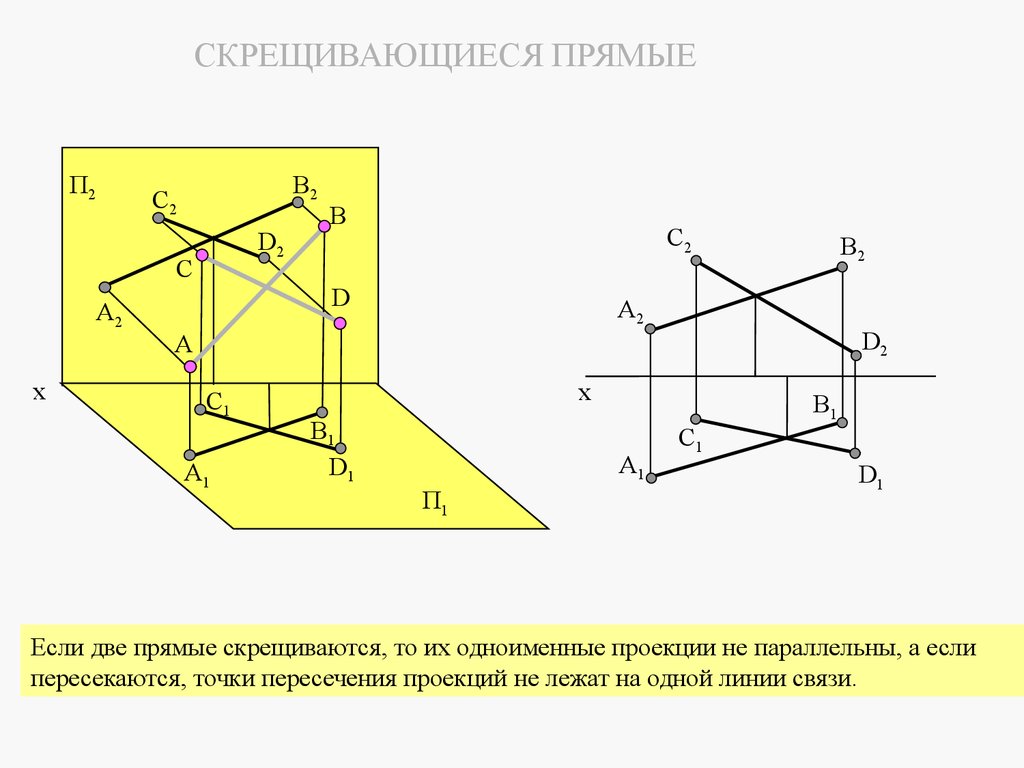
3.4.3 Скрещивающиеся прямыеДве прямые скрещиваются, если их одноименные проекции не параллельны, а если
пересекаются, то проекции точек пересечения не лежат на одной линии связи.
C2
A2
x
B2
[AB] [CD]
D2
A1
D1
C1
B1
Таким образом, по взаимному положению одноименных проекций двух прямых можно определить их
относительное положение в пространстве.
45.
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕП2
B2
C2
D2
C
A2
x
B
C2
D
B2
A2
D2
A
C1
A1
x
B1
D1
B1
A1
П1
C1
D1
Если две прямые скрещиваются, то их одноименные проекции не параллельны, а если
пересекаются, точки пересечения проекций не лежат на одной линии связи.
46.
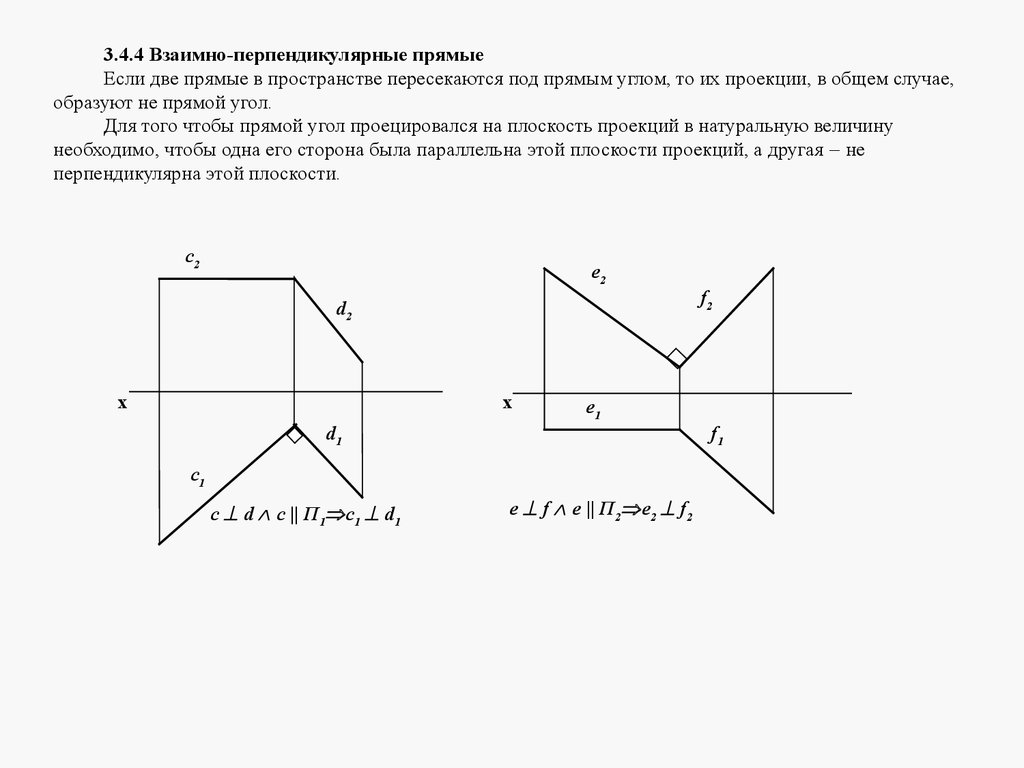
3.4.4 Взаимно-перпендикулярные прямыеЕсли две прямые в пространстве пересекаются под прямым углом, то их проекции, в общем случае,
образуют не прямой угол.
Для того чтобы прямой угол проецировался на плоскость проекций в натуральную величину
необходимо, чтобы одна его сторона была параллельна этой плоскости проекций, а другая не
перпендикулярна этой плоскости.
c2
e2
d2
x
x
d1
e1
c1
с d c || П1 с1 d1
е f e || П2 e2 f2
f2
f1
47.
ПРОЕЦИРОВАНИЕ ПРЯМОГО УГЛАДля того, чтобы прямой угол проецировался на плоскость проекций в
натуральную величину, необходимо, чтобы одна его сторона была
параллельна этой плоскости проекций, а другая- не перпендикулярна этой
плоскости.
c2
e2
d2
x
x
d1
e1
f1
c1
с d ^ c || П1 с1 d1
f2
е f ^ e || П2 e2 f2
48.
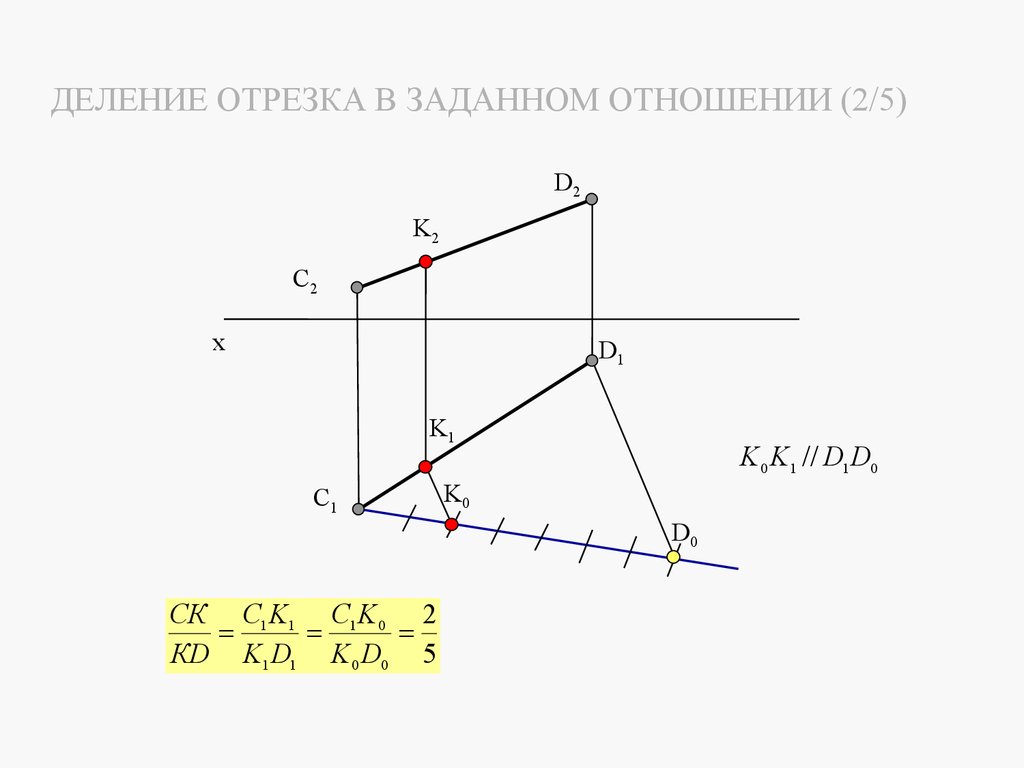
3.5 ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ В ЗАДАННОМ ОТНОШЕНИИВ соответствии со свойствами параллельных проекций отношение отрезков прямой равно отношению
проекций этих отрезков. На основании этого задача деления отрезка прямой в заданном отношении на
чертеже решается путем деления в этом же отношении проекций этого отрезка.
Рассмотрим пример деления отрезка прямой CD в отношении 2:5.
Проведем через точку С1 вспомогательную прямую под любым углом к горизонтальной проекции C1D1 и
отложим на ней семь равных отрезков произвольной длины. Отметим точку К 0, делящую вспомогательную
прямую в отношении 2:5.
Соединив точку D0 с точкой D1 и проведя через точку К0 прямую, параллельную прямой D0D1, получим
точку К1, которая делит горизонтальную проекцию C1D1 в заданном отношении. Фронтальную проекцию К 2
находим с помощью вертикальной линии связи.
D2
K2
C2
x
D1
K1
C1
K0
D0
49.
ДЕЛЕНИЕ ОТРЕЗКА В ЗАДАННОМ ОТНОШЕНИИ (2/5)D2
K2
C2
x
D1
K1
C1
K 0 K1 // D1 D0
K0
D0
СК С1 K1 C1 K 0 2
КD K1 D1 K 0 D0 5
50.
4. ЛЕКЦИЯ № 3. ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ. ПРЯМАЯ И ТОЧКА ВПЛОСКОСТИ
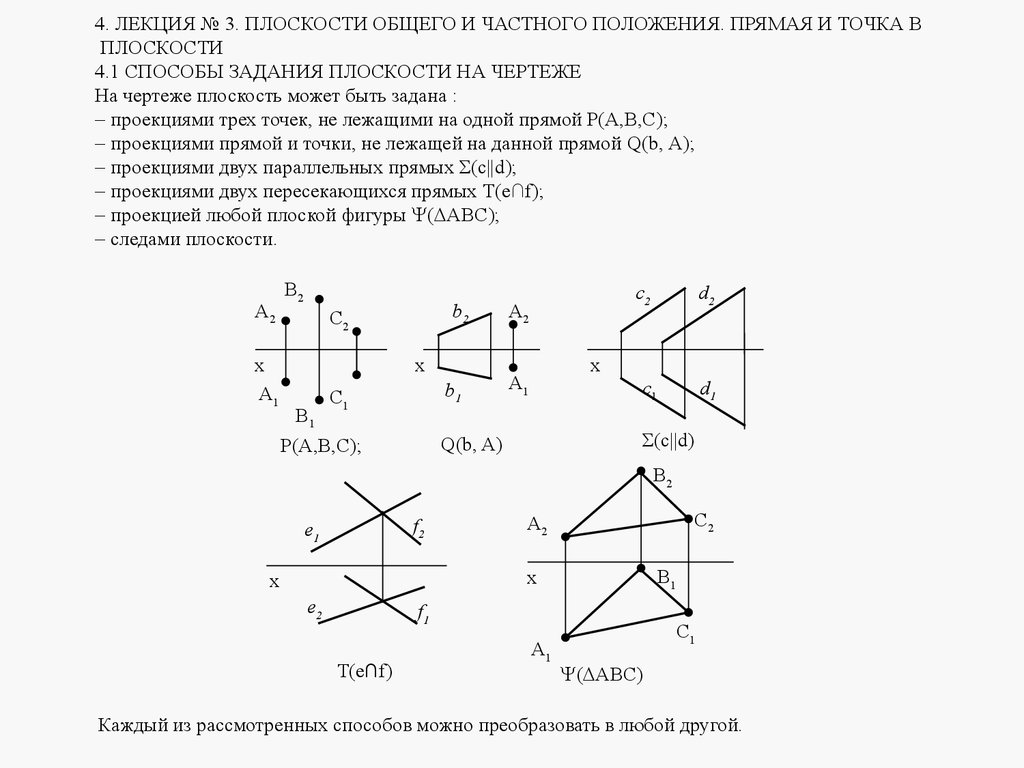
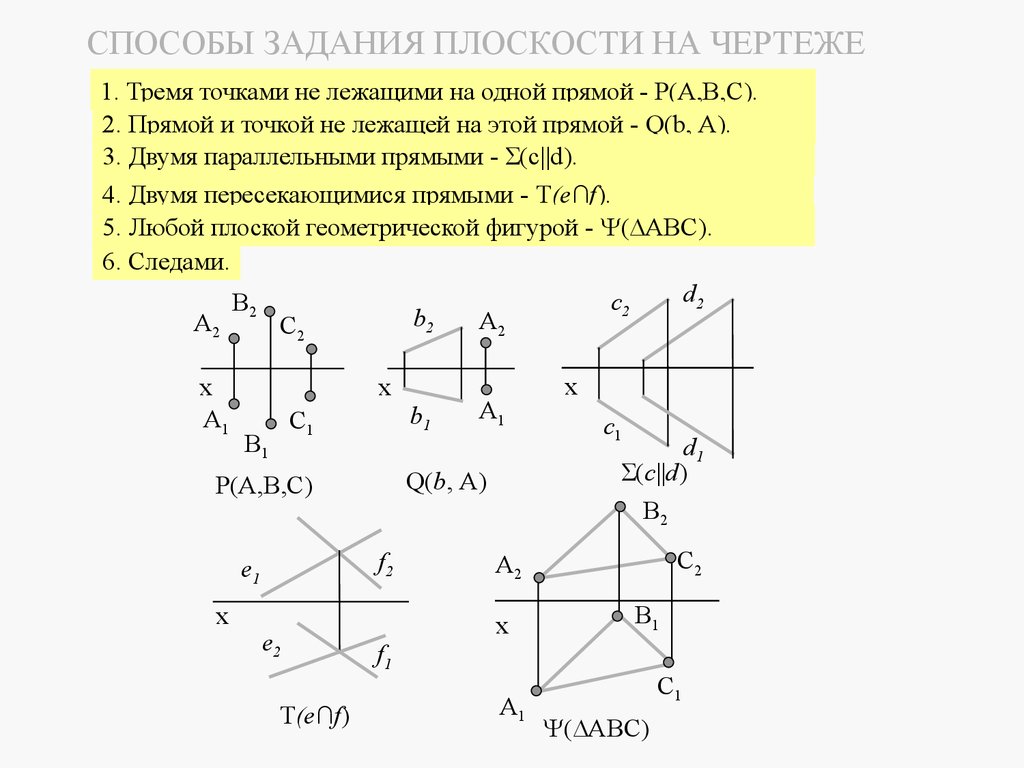
4.1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ
На чертеже плоскость может быть задана :
проекциями трех точек, не лежащими на одной прямой Р(А,В,С);
проекциями прямой и точки, не лежащей на данной прямой Q(b, A);
проекциями двух параллельных прямых Σ(с||d);
проекциями двух пересекающихся прямых T(e∩f);
проекцией любой плоской фигуры ( ABC);
следами плоскости.
А2
х
А1
В2
b2
С2
х
В1
b1
С1
c2
А2
х
А1
d1
c1
Σ(с||d)
Q(b, A)
Р(А,В,С);
d2
В2
f2
e1
С2
А2
В1
х
х
e2
f1
T(e∩f)
А1
С1
( ABC)
Каждый из рассмотренных способов можно преобразовать в любой другой.
51.
СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ1. Тремя точками не лежащими на одной прямой - Р(А,В,С).
2. Прямой и точкой не лежащей на этой прямой - Q(b, A).
3. Двумя параллельными прямыми - Σ(с||d).
4. Двумя пересекающимися прямыми - T(e∩f).
5. Любой плоской геометрической фигурой - ( ABC).
6. Следами.
d2
c2
В2
b2
А2
А2
С2
х
А1
х
b1
С1
В1
f2
х
e2
T(e∩f)
c1
d1
Σ(с||d)
В2
Q(b, A)
Р(А,В,С)
e1
А1
х
С2
А2
х
В1
f1
А1
С1
( ABC)
52.
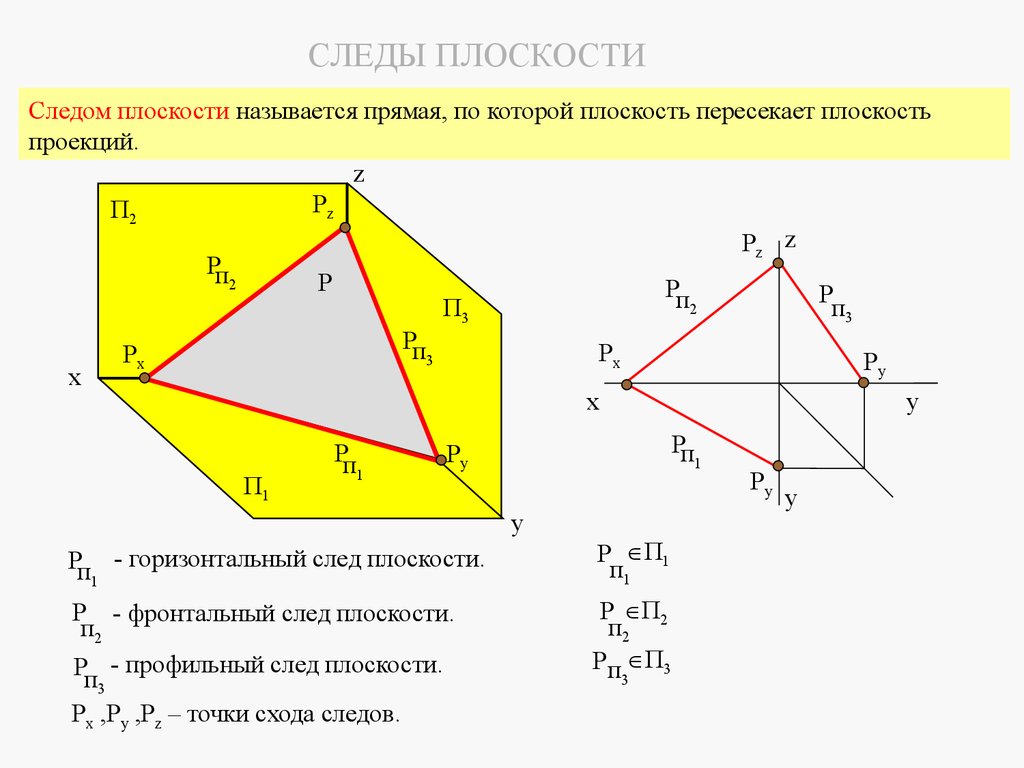
4.2 СЛЕДЫ ПЛОСКОСТИСледом плоскости называется прямая линия, по которой плоскость пересекает плоскость
проекций.
z
Рz
П2
Рп
2
x
Р
П3
Рп
3
Рх
П1
Рп
1
Рy
Рп горизонтальный след плоскости Р
1
Рп фронтальный след плоскости Р
2
Рп профильный след плоскости Р
3
y
53.
СЛЕДЫ ПЛОСКОСТИСледом плоскости называется прямая, по которой плоскость пересекает плоскость
проекций.
z
Рz
П2
Рz z
Рп
2
Р
Рп
Р
2
п3
П3
Рп
Рx
Рх
3
Рy
x
x
y
П1
Рп
1
Рп
1
Рy
y
Рп - горизонтальный след плоскости.
1
Р П1
п1
Р - фронтальный след плоскости.
п2
Рп - профильный след плоскости.
3
Рx ,Рy ,Pz – точки схода следов.
Р П2
п2
Рп П3
3
Рy
y
54.
Плоскость Р называется плоскостью общего положения, так как она не параллельна ине перпендикулярна ни одной из плоскостей проекций.
Точки Рх, Рy, Рz, в которых следы плоскости пересекают оси проекций, называются
точками схода следов.
Рz
Рп
z
Рп
3
2
Рx
Рy
x
y
Рп
1
Рy
y
Из анализа следов видно, что горизонтальная проекция горизонтального следа совпадает с
самим следом, а фронтальная проекция – с осью х. Фронтальная проекция фронтального следа
совпадает с самим следом, а горизонтальная с осью х.
Следы плоскости можно построить при любом из способов ее задания. Для построения
следа плоскости достаточно построить две точки, принадлежащие одновременно заданной
плоскости и плоскостям проекций. Такими точками могут быть следы прямой, принадлежащей
этой плоскости.
55.
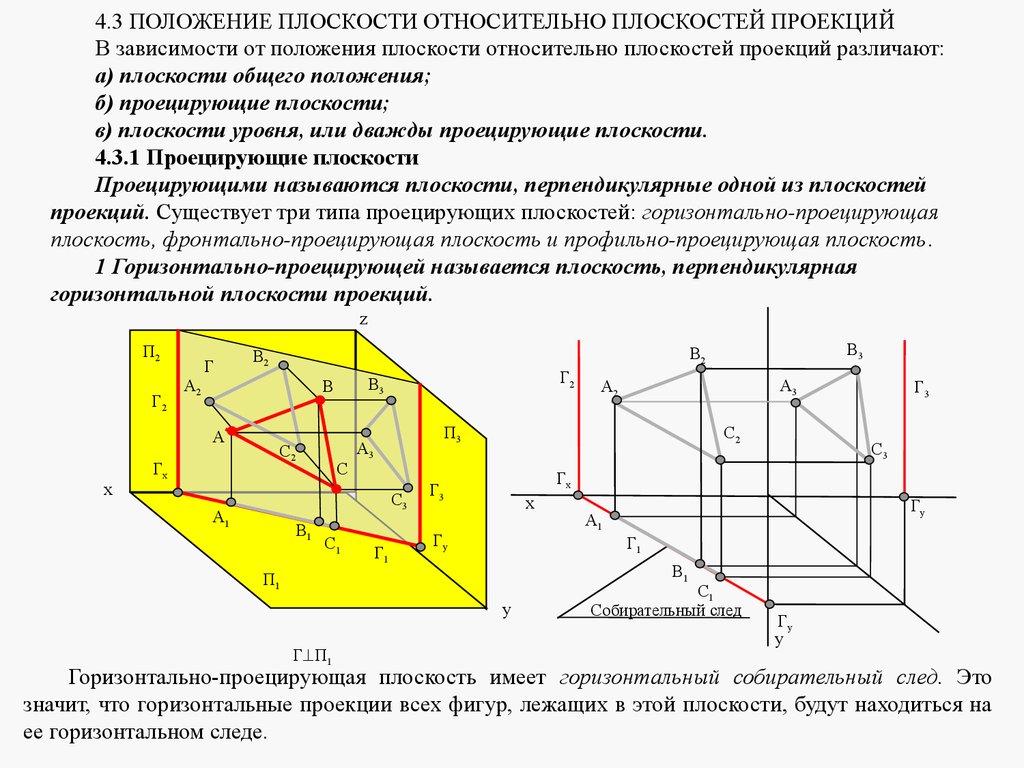
4.3 ПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙВ зависимости от положения плоскости относительно плоскостей проекций различают:
а) плоскости общего положения;
б) проецирующие плоскости;
в) плоскости уровня, или дважды проецирующие плоскости.
4.3.1 Проецирующие плоскости
Проецирующими называются плоскости, перпендикулярные одной из плоскостей
проекций. Существует три типа проецирующих плоскостей: горизонтально-проецирующая
плоскость, фронтально-проецирующая плоскость и профильно-проецирующая плоскость.
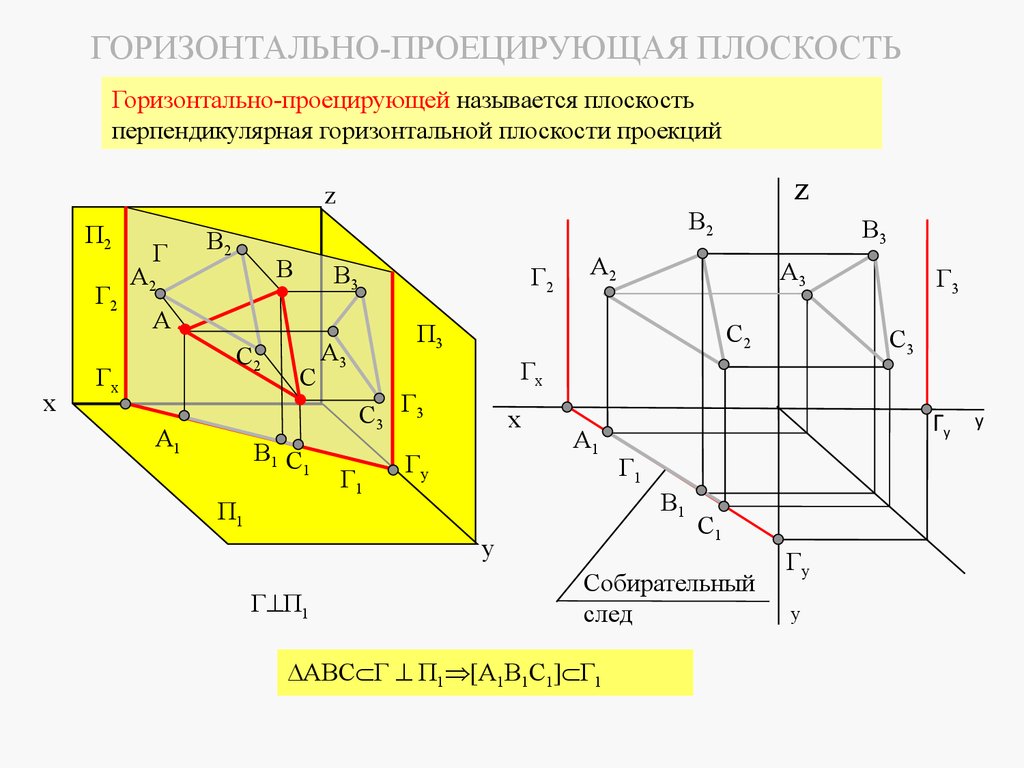
1 Горизонтально-проецирующей называется плоскость, перпендикулярная
горизонтальной плоскости проекций.
z
П2
Г2
Г
A2
x
Гх
С2
Г2
В3
B
A
B3
B2
В2
C
П3
A3
С3
A1
B1
C1
Г1
C2
Г3
C3
Гx
Г3
x
Гy
Гy
A1
Г1
B1
П1
y
Г П1
A3
A2
C1
Собирательный след
Гy
y
Горизонтально-проецирующая плоскость имеет горизонтальный собирательный след. Это
значит, что горизонтальные проекции всех фигур, лежащих в этой плоскости, будут находиться на
ее горизонтальном следе.
56.
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬГоризонтально-проецирующей называется плоскость
перпендикулярная горизонтальной плоскости проекций
z
П2
Г2
x
Г
В2
B
A2
B2
В3
Г2
A
С2
Гх
A1
C
B1 C
1
П1
A3
П3
A3
C2
x
Гy
A1
Гy
Г1
B1
C1
Собирательный
след
ABC Г П1 [A1B1C1] Г1
Г3
C3
Гx
С3 Г 3
Г1
B3
A2
y
Г П1
z
Гy
y
y
57.
2 Фронтально-проецирующей называется плоскость, перпендикулярнаяфронтальной плоскости проекций.
z
Фz
П2
B2
Ф2
Ф
B
A2
Фx
x
z
Cобирательный
Ф2
B
2
след
Ф3
B3
A3
A
Ф1 A 1
П1
B1
Ф П2
x
Фx
Фz
z
B3
A2
A3
A1
П3
y
Ф1
[AB] Ф П2 [A2B2] Ф2
Ф3
B1
y
y
58.
ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬФронтально-проецирующей называется плоскость
перпендикулярная фронтальной плоскости проекций
z
Фz
П2
B2
Ф2
B
A2
Фx
x
Cобирательный
след
Ф3
Ф
B3
Ф 1 A1
П1
B1
Ф П2
A3
Фx
y
x
A1
П3
y
Ф3
B3
A2
A3
A
B2
Ф2
Фz
z
Ф1
[AB] Ф П2 [A2B2] Ф2
B1
y
59.
3 Профильно-проецирующей называется плоскость, перпендикулярная профильнойплоскости проекций.
z
z
П2
Σ2
Σ2
А2
Σz
Σ3
A
A3
Σy
x
А1
П1
Σ1
Σy
y
A1
П3
y
П3
Собирательный
след
A3
A2
Σ3
x
Σz
Σ1
Σy
y
A Σ П3 А3 Σ3
Важным свойством проецирующей плоскости является то, что она имеет
собирательный след.
60.
ПРОФИЛЬНО-ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬПрофильно-проецирующей называется плоскость перпендикулярная
профильной плоскости проекций
z
z
Σ2
П2
Σ2
Σz
Σ3
А2
A
A3
Σy
x
А1
П1
Σ1
Σy
Собирательный
след
A3
A2
Σ3
x
Σz
y
A1
П3
y
Σ1
П3
A Σ П3 А3 Σ3
Σy
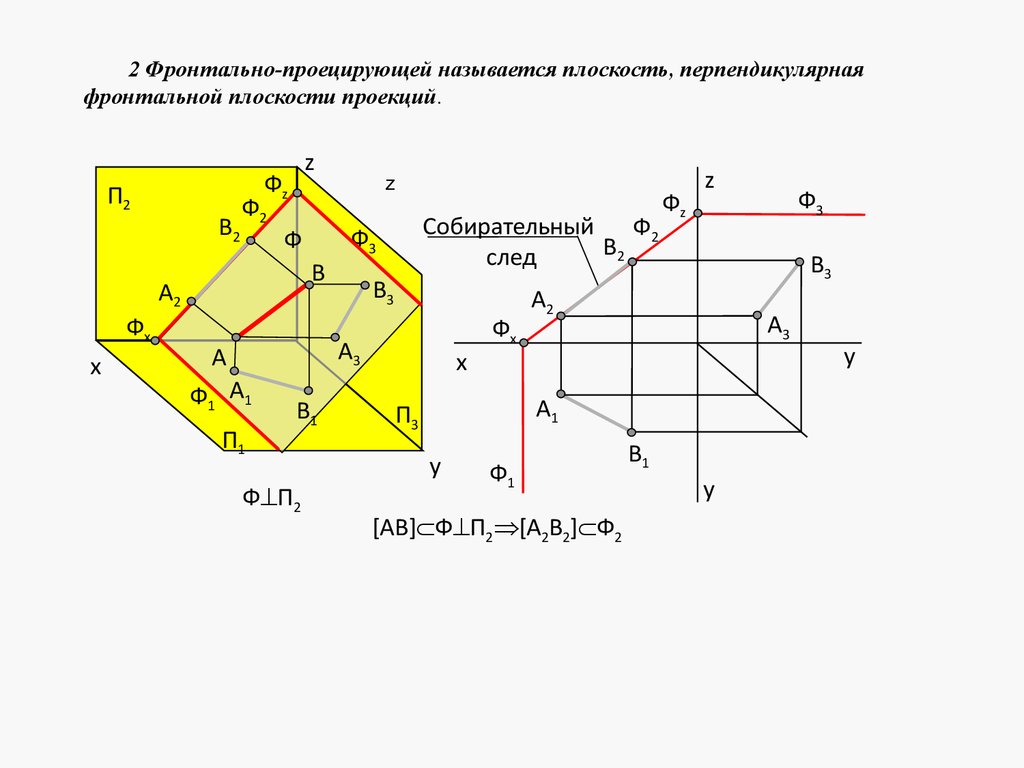
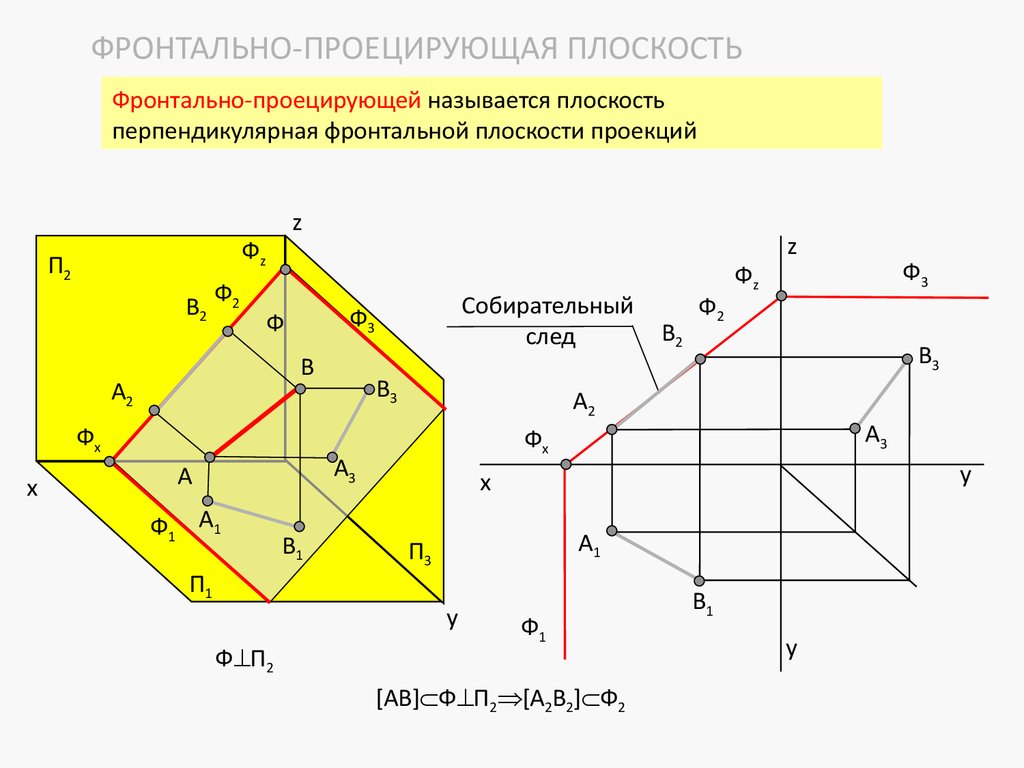
y
61.
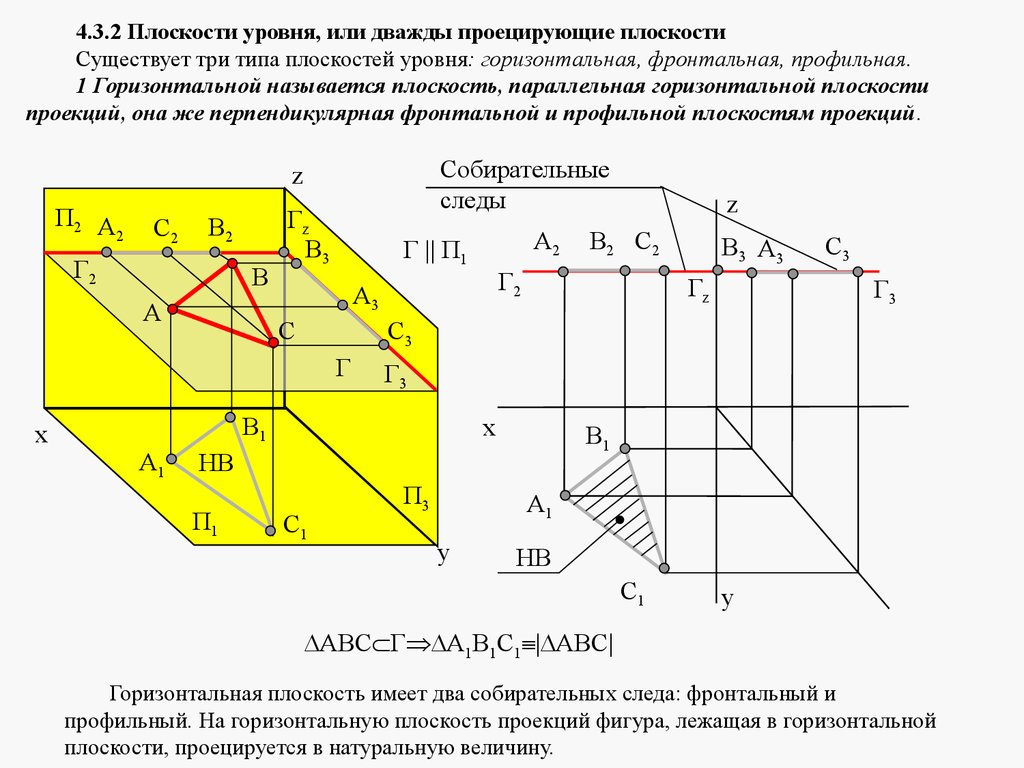
4.3.2 Плоскости уровня, или дважды проецирующие плоскостиСуществует три типа плоскостей уровня: горизонтальная, фронтальная, профильная.
1 Горизонтальной называется плоскость, параллельная горизонтальной плоскости
проекций, она же перпендикулярная фронтальной и профильной плоскостям проекций.
Собирательные
следы
z
П2 A
2
C2
B2
Г2
B
A
Гz
B3
C
Гz
C3
Г3
Г3
x
B1
НВ
П1
B 3 A3
C3
B1
A1
B2 C2
Г2
A3
Г
x
A2
Г П1
z
C1
П3
A1
y
НВ
C1
y
АВС Г А1В1С1 | АВС|
Горизонтальная плоскость имеет два собирательных следа: фронтальный и
профильный. На горизонтальную плоскость проекций фигура, лежащая в горизонтальной
плоскости, проецируется в натуральную величину.
62.
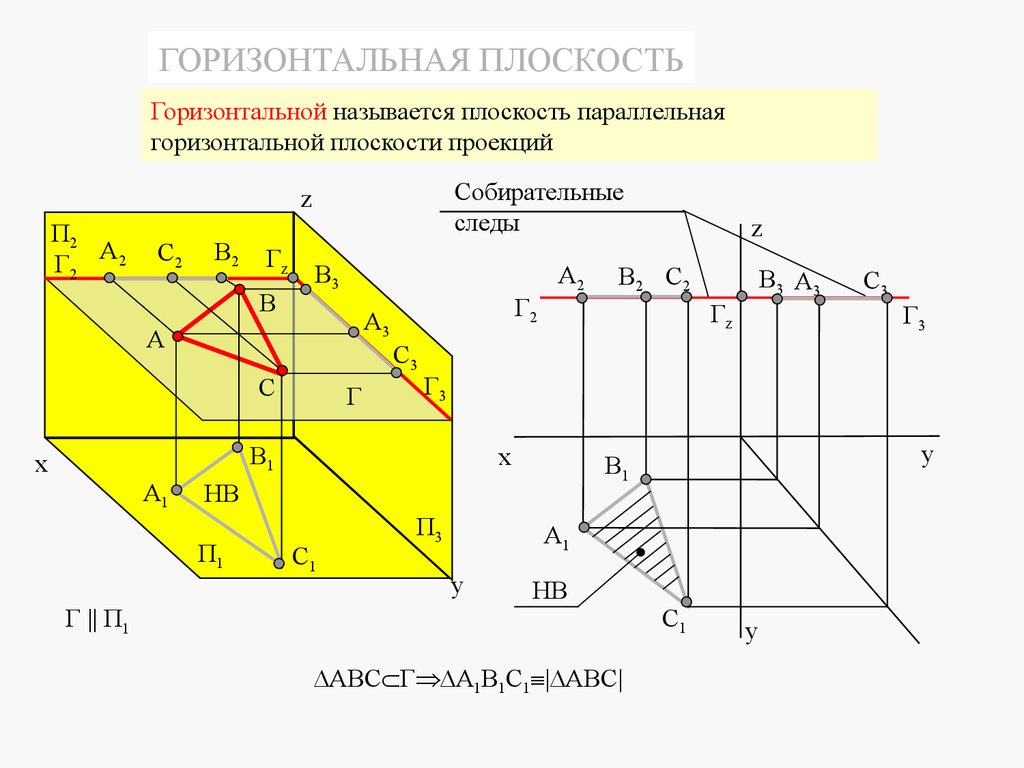
ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬГоризонтальной называется плоскость параллельная
горизонтальной плоскости проекций
Собирательные
следы
z
П2
A2
Г2
C2
B2
Гz
B
B3
A2
Г2
A3
A
C3
C
Г
A1
Г П1
x
C1
B 3 A3
Гz
C3
Г3
П3
y
B1
НВ
П1
B2 C2
Г3
B1
x
z
A1
y
НВ
АВС Г А1В1С1 | АВС|
C1
y
63.
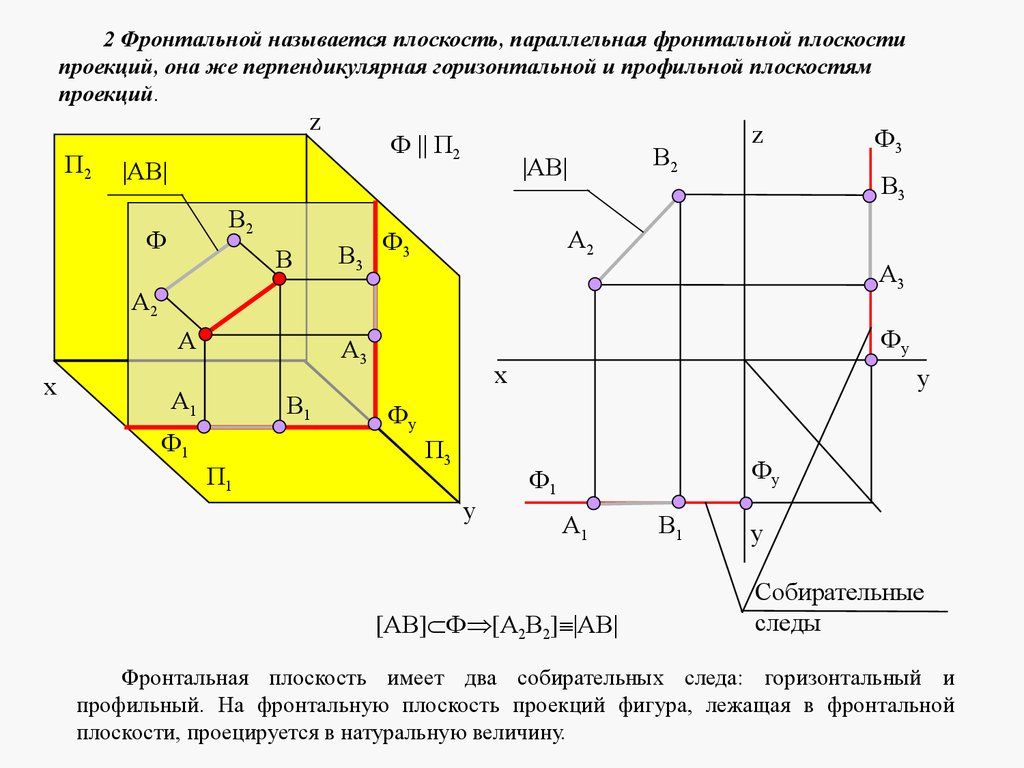
2 Фронтальной называется плоскость, параллельная фронтальной плоскостипроекций, она же перпендикулярная горизонтальной и профильной плоскостям
проекций.
z
П2
Ф П2
|AB|
B2
Ф
B
B3
B2
|AB|
z
B3
A2
Ф3
A3
A2
A
x
Фy
A3
A1
B1
Ф1
П1
Ф3
x
y
Фy
П3
y
Фy
Ф1
A1
[АВ] Ф [А2В2] |АВ|
B1
y
Собирательные
следы
Фронтальная плоскость имеет два собирательных следа: горизонтальный и
профильный. На фронтальную плоскость проекций фигура, лежащая в фронтальной
плоскости, проецируется в натуральную величину.
64.
ФРОНТАЛЬНАЯ ПЛОСКОСТЬФронтальной называется плоскость параллельная фронтальной
плоскости проекций
z
П2
B2
|AB|
|AB|
B2
Ф
B
B3
z
B3
A2
Ф3
A3
A2
A
x
Фy
A3
A1
B1
Ф1
П1
Ф3
x
y
Фy
П3
y
Фy
Ф1
A1
Ф П2
[АВ] Ф [А2В2] |АВ|
B1
y
Собирательные
следы
65.
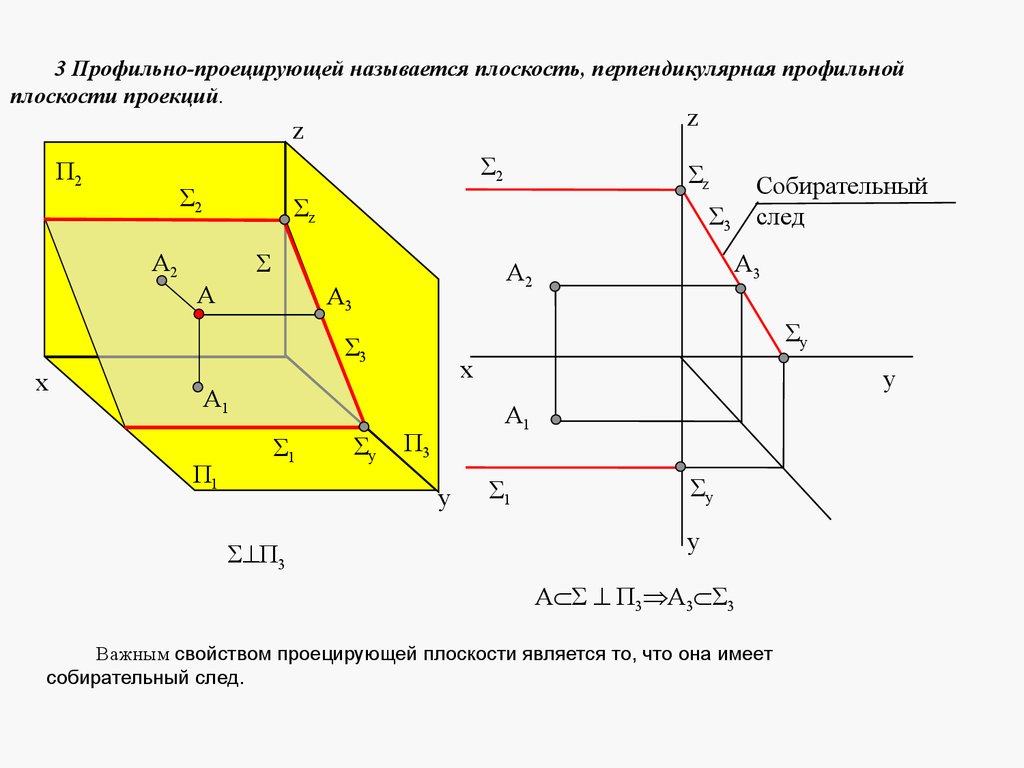
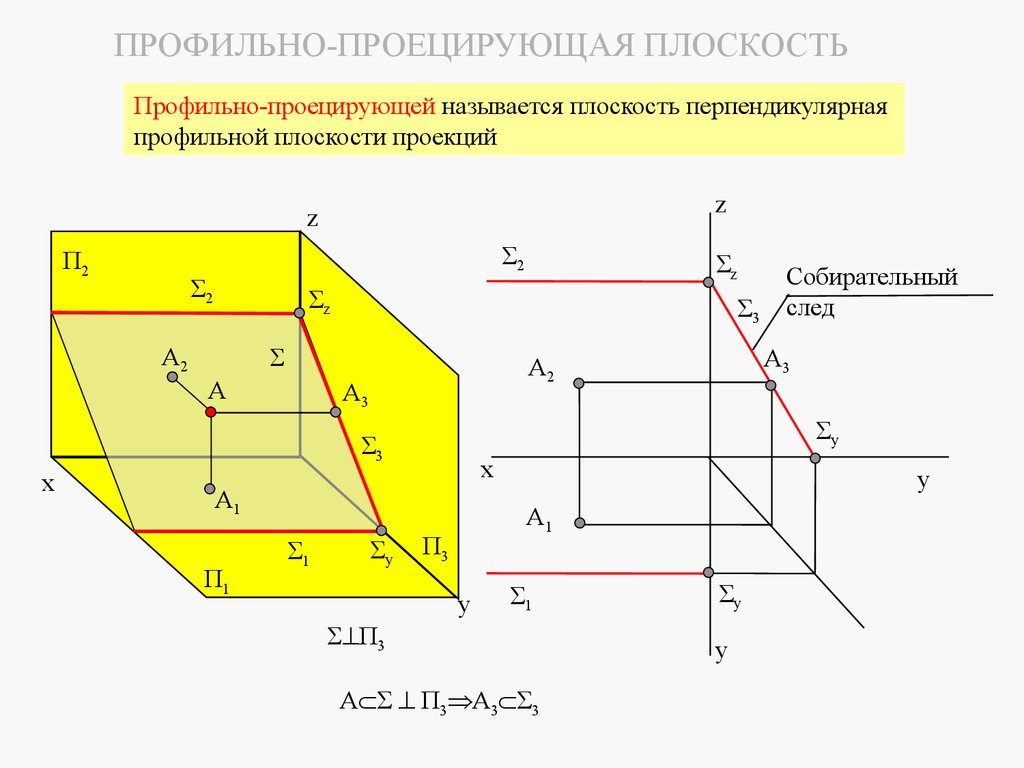
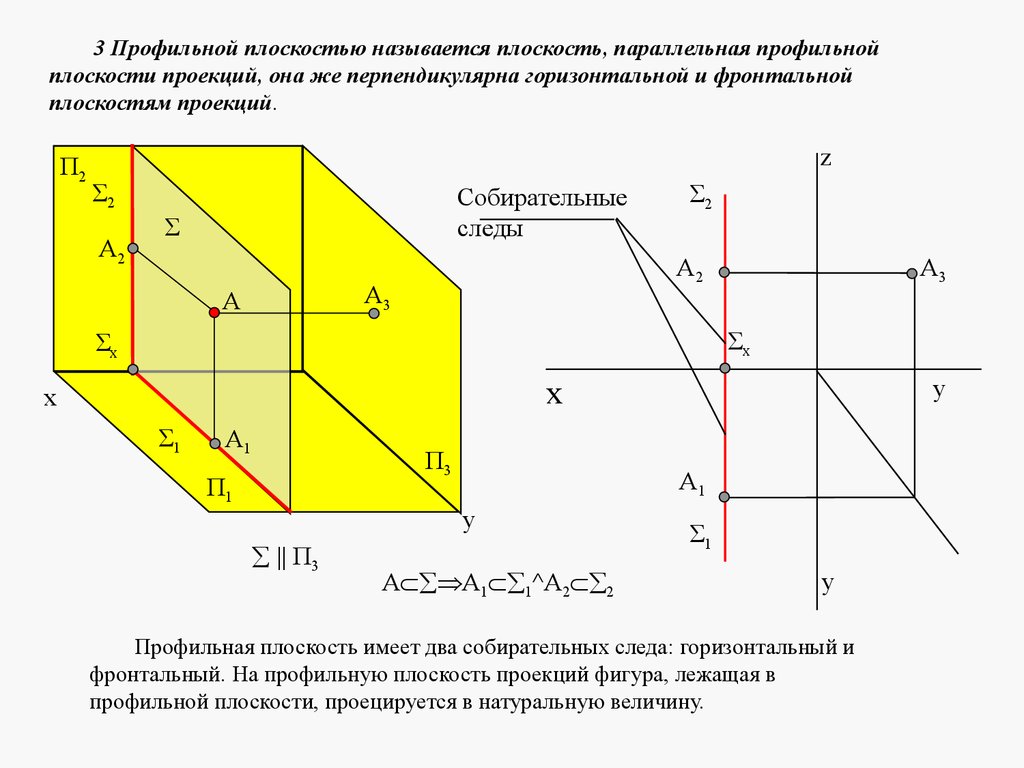
3 Профильной плоскостью называется плоскость, параллельная профильнойплоскости проекций, она же перпендикулярна горизонтальной и фронтальной
плоскостям проекций.
П2
z
Σ2
А2
Собирательные
следы
Σ
A2
А3
А
Σ2
A3
Σx
Σx
x
x
Σ1
А1
П3
П1
A1
y
|| П3
y
А А1 1^А2 2
Σ1
y
Профильная плоскость имеет два собирательных следа: горизонтальный и
фронтальный. На профильную плоскость проекций фигура, лежащая в
профильной плоскости, проецируется в натуральную величину.
66.
ПРОФИЛЬНАЯ ПЛОСКОСТЬПрофильной называется плоскость параллельная профильной
плоскости проекций
z
П2
z
Σ2
А2
Собирательные
следы
Σ
A2
А3
А
Σ2
A3
Σx
Σx
x
x
Σ1
А1
П3
П1
A1
y
|| П3
А А1 1^А2 2
y
Σ1
y
67.
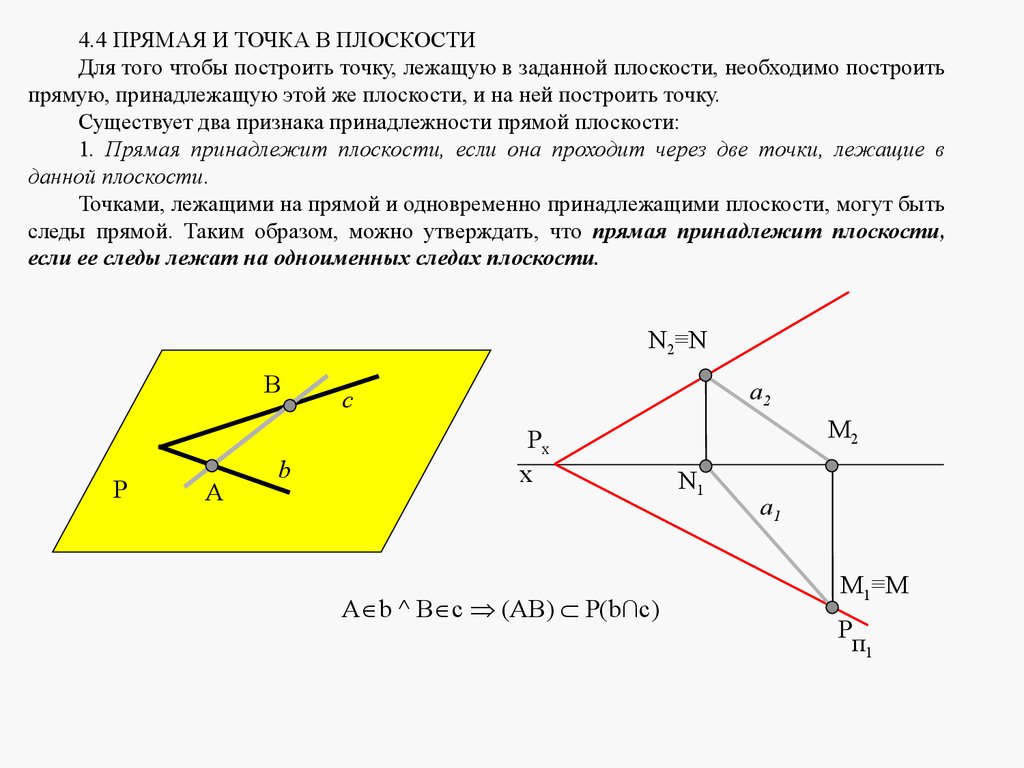
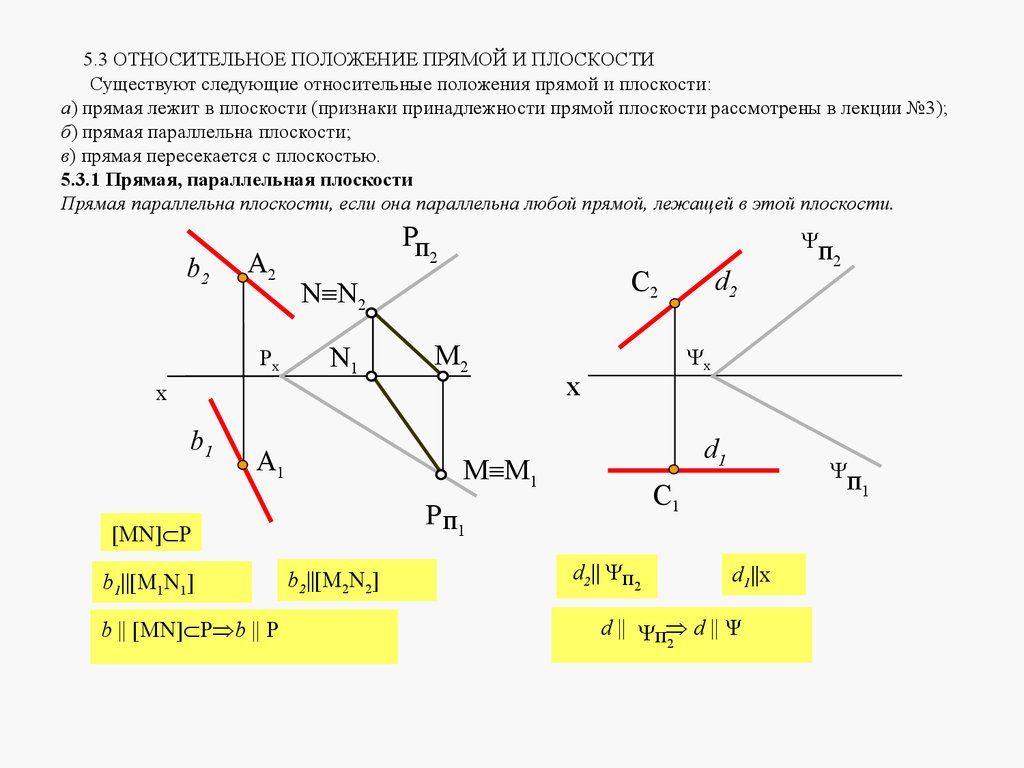
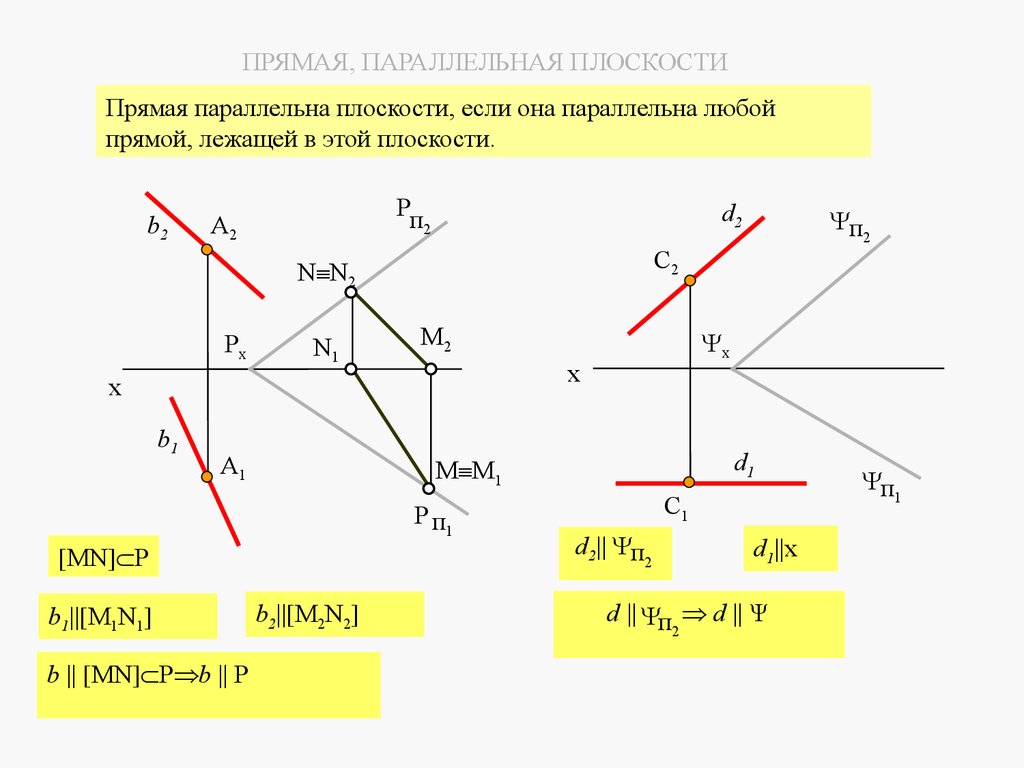
4.4 ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИДля того чтобы построить точку, лежащую в заданной плоскости, необходимо построить
прямую, принадлежащую этой же плоскости, и на ней построить точку.
Существует два признака принадлежности прямой плоскости:
1. Прямая принадлежит плоскости, если она проходит через две точки, лежащие в
данной плоскости.
Точками, лежащими на прямой и одновременно принадлежащими плоскости, могут быть
следы прямой. Таким образом, можно утверждать, что прямая принадлежит плоскости,
если ее следы лежат на одноименных следах плоскости.
N2≡N
B
Р
A
b
a2
c
Рx
x
А b ^ B c (АВ) Р(b∩c)
M2
N1
a1
M1≡M
Р
п1
68.
ПЕРВЫЙ ПРИЗНАК ПРИНАДЛЕЖНОСТИ ПРЯМОЙ ПЛОСКОСТИПрямая принадлежит плоскости, если она проходит через две точки
лежащие в этой плоскости.
Если плоскость задана следами, то такими точками могут быть
следы этой прямой.
Рп
2
N2≡N
B
Р
A
a2
c
b
Рx
x
M2
N1
a1
M1≡M
А b ^ B c (АВ) Р(b∩c)
М Рп ^ N Рп (МN) Р
2
1
Р
п1
69.
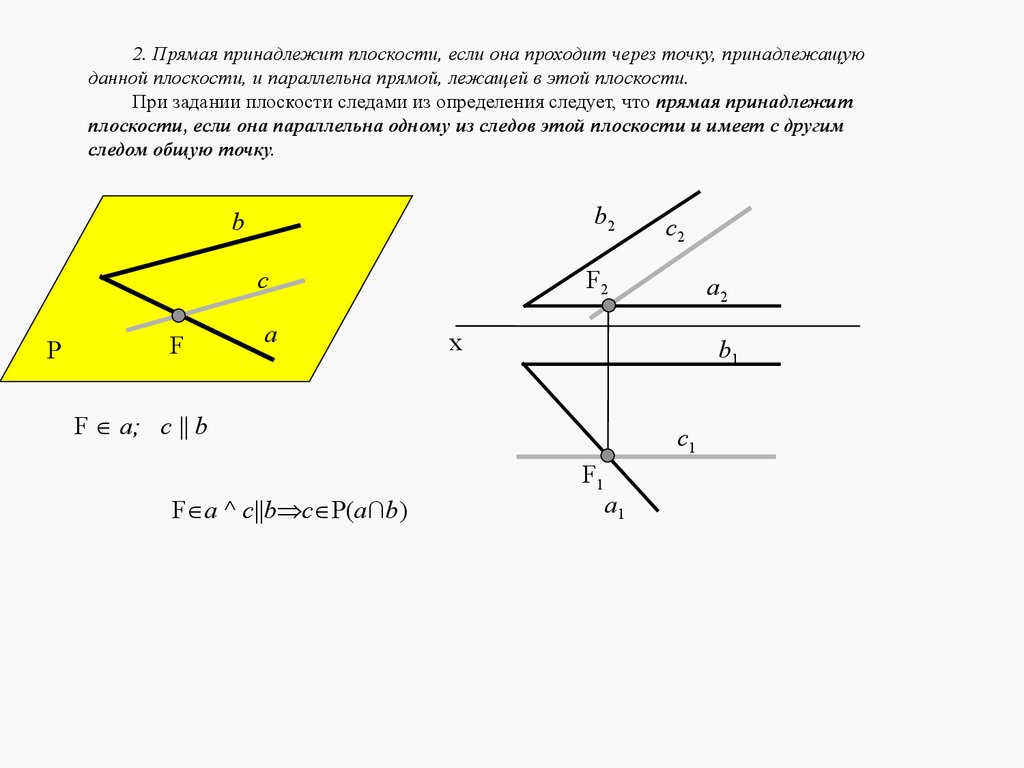
2. Прямая принадлежит плоскости, если она проходит через точку, принадлежащуюданной плоскости, и параллельна прямой, лежащей в этой плоскости.
При задании плоскости следами из определения следует, что прямая принадлежит
плоскости, если она параллельна одному из следов этой плоскости и имеет с другим
следом общую точку.
b2
b
c
Р
F
а
F2
a2
x
b1
F а; с b
с1
F1
F a ^ c b c P(a∩b)
c2
a1
70.
ВТОРОЙ ПРИЗНАК ПРИНАДЛЕЖНОСТИ ПРЯМОЙ ПЛОСКОСТИПрямая принадлежит плоскости, если она проходит через точку,
принадлежащую данной плоскости, и параллельна прямой, лежащей в
этой плоскости.
b2
b
F2
c
Р
F
а
a2
x
b1
F а; с b
с1
F1
F a ^ c b c P(a∩b)
c2
a1
71.
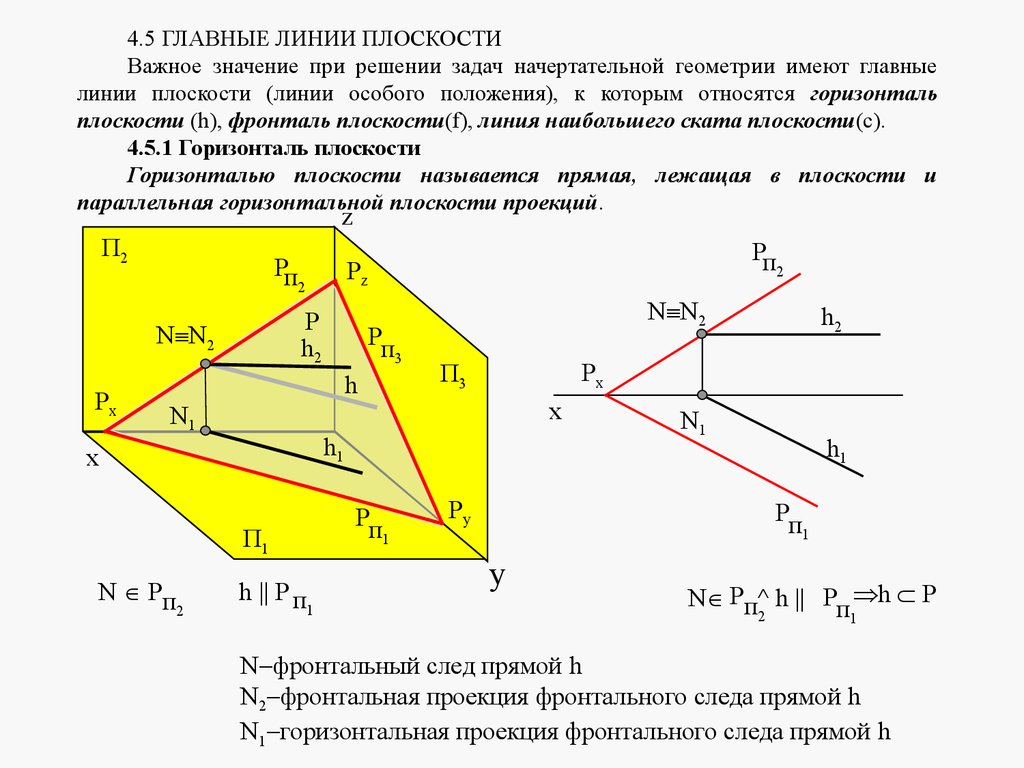
4.5 ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИВажное значение при решении задач начертательной геометрии имеют главные
линии плоскости (линии особого положения), к которым относятся горизонталь
плоскости (h), фронталь плоскости(f), линия наибольшего ската плоскости(c).
4.5.1 Горизонталь плоскости
Горизонталью плоскости называется прямая, лежащая в плоскости и
параллельная горизонтальной плоскости проекций.
z
П2
Рп
2
Рх
Рz
Р
h2
N N2
Рп
2
Рп
3
h
N1
Рп
1
П1
2
h Р п
1
h2
Рх
П3
х
h1
x
N Pп
N N2
Рy
N1
h1
Рп
1
y
N Рп^ h || Рп h P
2
1
N фронтальный след прямой h
N2 фронтальная проекция фронтального следа прямой h
N1 горизонтальная проекция фронтального следа прямой h
72.
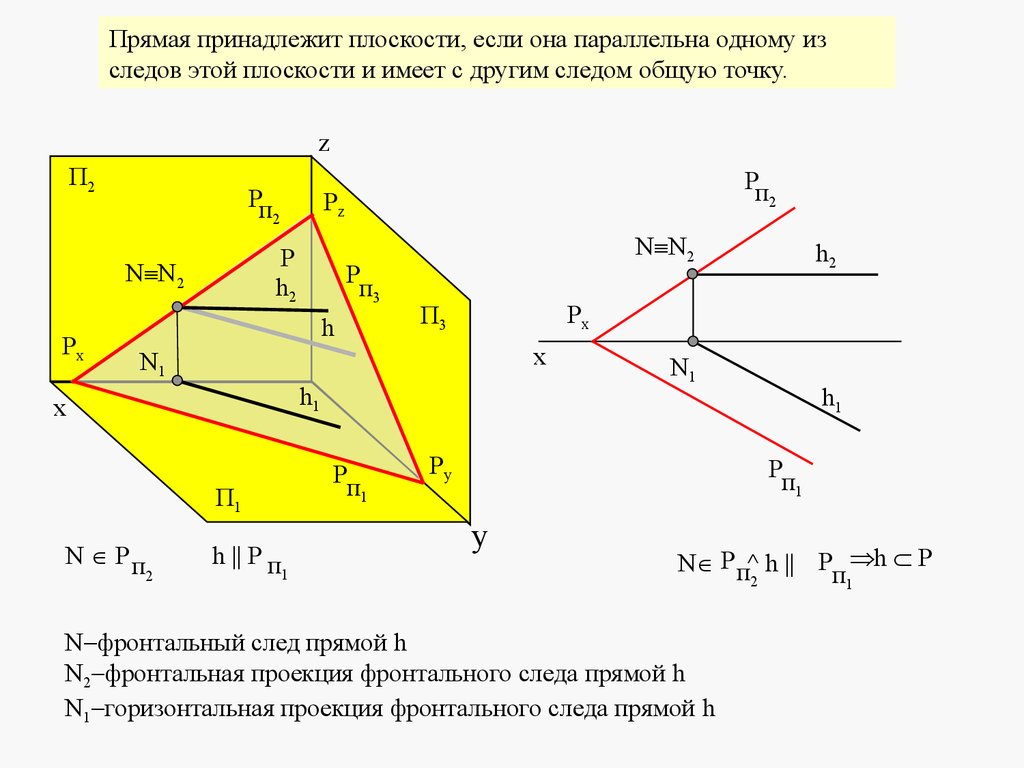
Прямая принадлежит плоскости, если она параллельна одному изследов этой плоскости и имеет с другим следом общую точку.
z
П2
Рп
2
Р
h2
N N2
Рх
Рп
2
Рz
Р
п3
h
N N2
Рх
П3
х
N1
h1
x
Р
п1
П1
N Pп
2
h Р п
1
h2
N1
Рy
h1
Р
п1
y
N Р п^ h || Рп h P
2
1
N фронтальный след прямой h
N2 фронтальная проекция фронтального следа прямой h
N1 горизонтальная проекция фронтального следа прямой h
73.
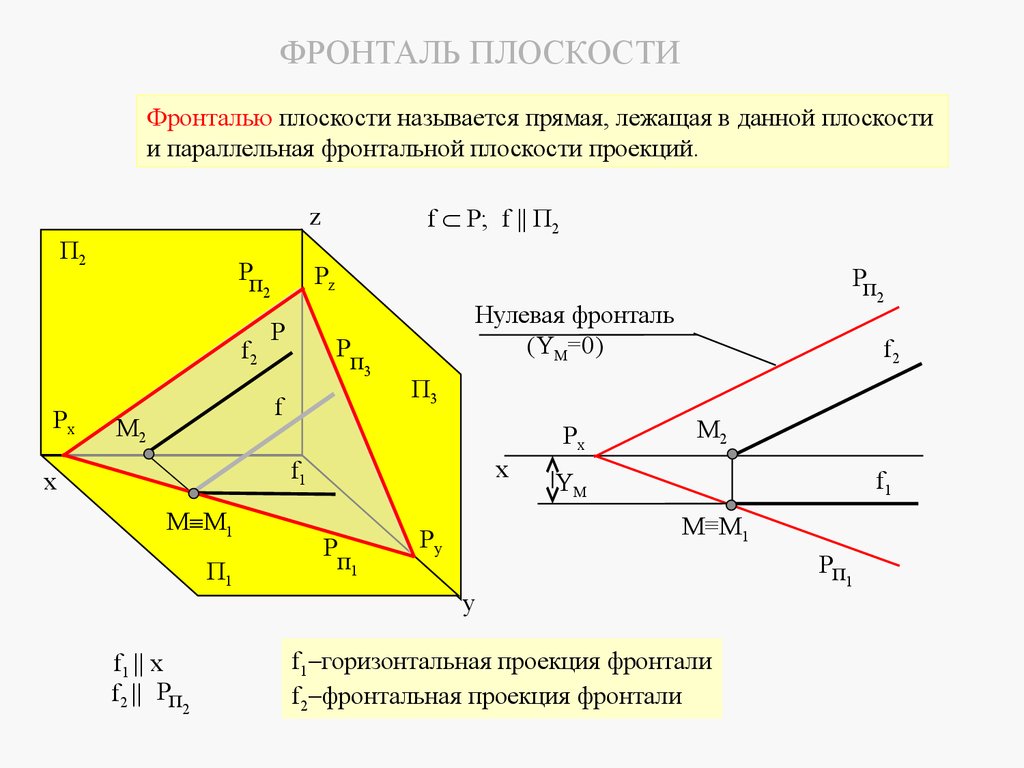
4.5.2 Фронталь плоскостиФронталью плоскости называется прямая, лежащая в данной плоскости и
параллельная фронтальной плоскости проекций.
f P; f П2
z
П2
Рп
2
f2
Рх
Рz
Р
Рп
3
f
M2
Нулевая фронталь
(YM=0)
M M1
Рx
x
П1
f1 x
f2 Рп2
Рп
1
f2
П3
f1
x
Рп
2
M2
f1
YM
M≡M1
Рy
y
f1 горизонтальная проекция фронтали
f2 фронтальная проекция фронтали
Рп
1
74.
ФРОНТАЛЬ ПЛОСКОСТИФронталью плоскости называется прямая, лежащая в данной плоскости
и параллельная фронтальной плоскости проекций.
f P; f П2
z
П2
Рп
2
f2
Рх
Рz
Р
Р
п3
f
M2
Нулевая фронталь
(YM=0)
x
f1
M M1
П1
f1 x
f2 Рп2
Р
п1
f2
П3
Рx
x
Рп
2
M2
f1
YM
M≡M1
Рy
y
f1 горизонтальная проекция фронтали
f2 фронтальная проекция фронтали
Рп
1
75.
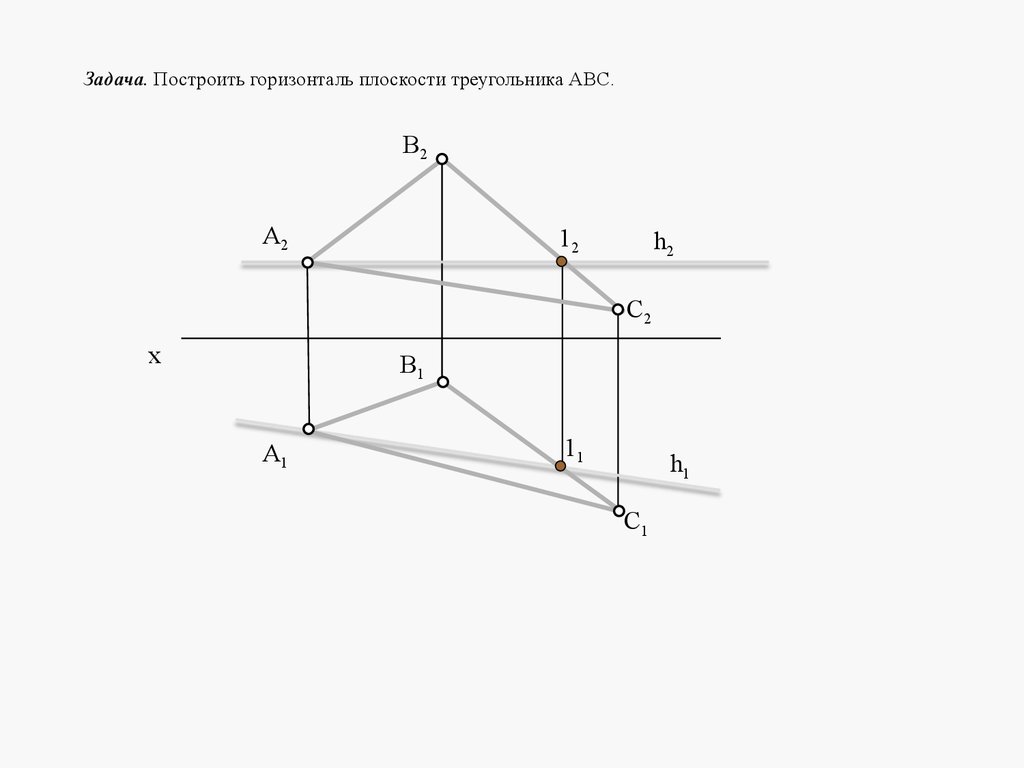
Задача. Построить горизонталь плоскости треугольника АВС.В2
A2
12
h2
С2
x
В1
A1
11
h1
С1
76.
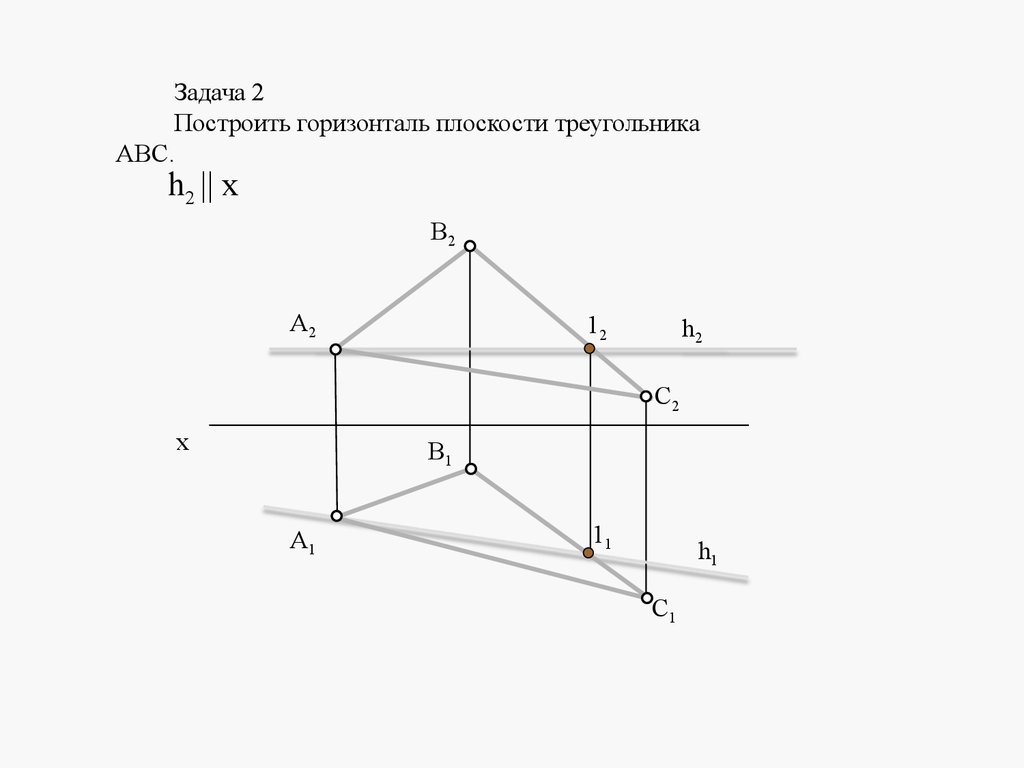
Задача 2Построить горизонталь плоскости треугольника
АВС.
h2 x
В2
A2
12
h2
С2
x
В1
A1
11
h1
С1
77.
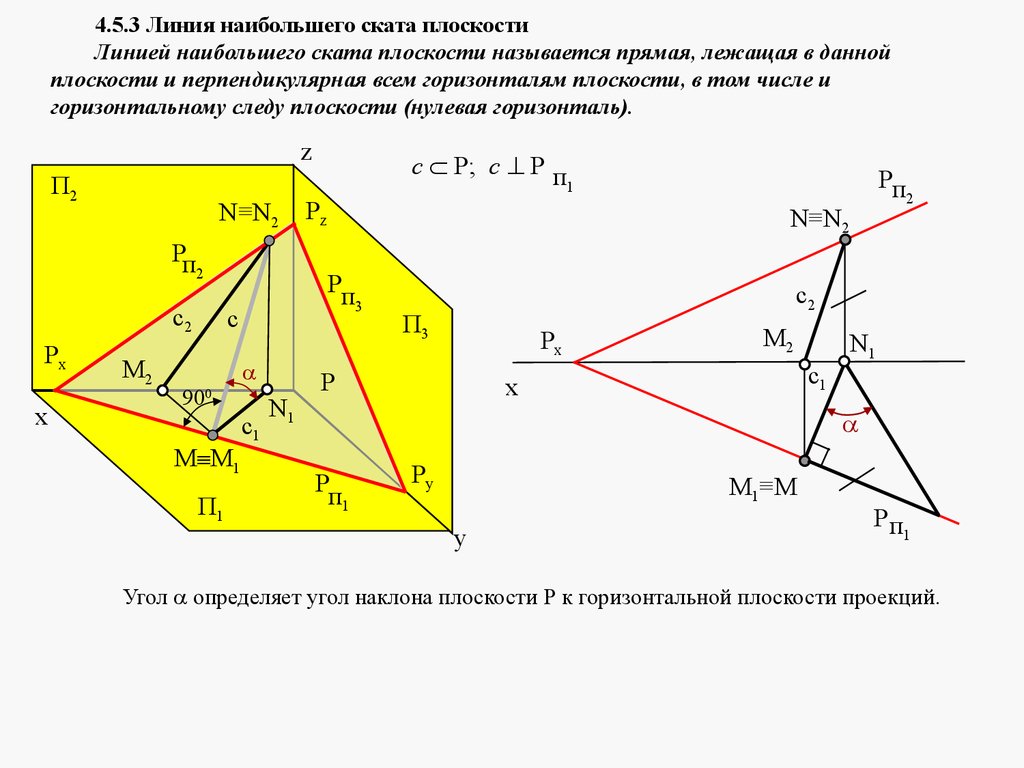
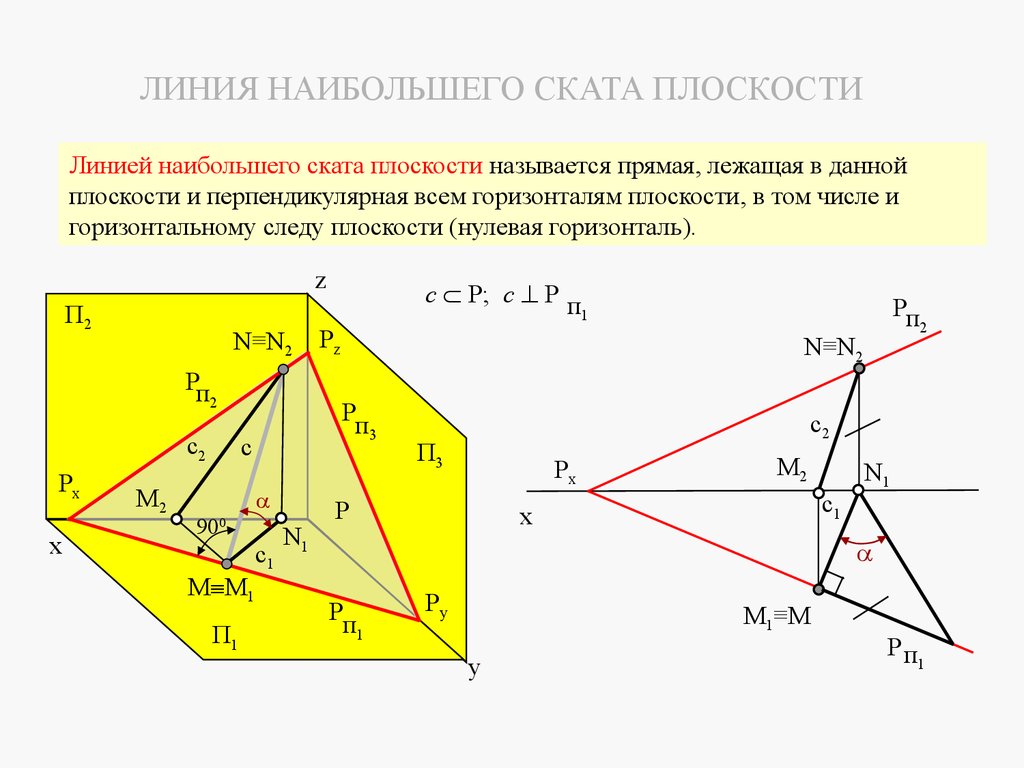
4.5.3 Линия наибольшего ската плоскостиЛинией наибольшего ската плоскости называется прямая, лежащая в данной
плоскости и перпендикулярная всем горизонталям плоскости, в том числе и
горизонтальному следу плоскости (нулевая горизонталь).
z
П2
N≡N2
Рп
2
с2
Рх
x
M2
90
0
с1
П1
Рz
N1
Рп
2
N≡N2
Р
п3
с
M M1
с Р; с Р п
1
c2
П3
Рx
Р
M2
c1
x
N1
Р
п1
Рy
M1≡M
y
Рп
1
Угол определяет угол наклона плоскости Р к горизонтальной плоскости проекций.
78.
ЛИНИЯ НАИБОЛЬШЕГО СКАТА ПЛОСКОСТИЛинией наибольшего ската плоскости называется прямая, лежащая в данной
плоскости и перпендикулярная всем горизонталям плоскости, в том числе и
горизонтальному следу плоскости (нулевая горизонталь).
z
П2
N≡N2
Рп
2
с2
Рх
x
M2
90
0
с1
П1
Рz
N1
Рп
2
N≡N2
Р
п3
с
M M1
с Р; с Р п
1
c2
П3
Рx
Р
M2
c1
x
N1
Р
п1
Рy
M1≡M
y
Рп
1
79.
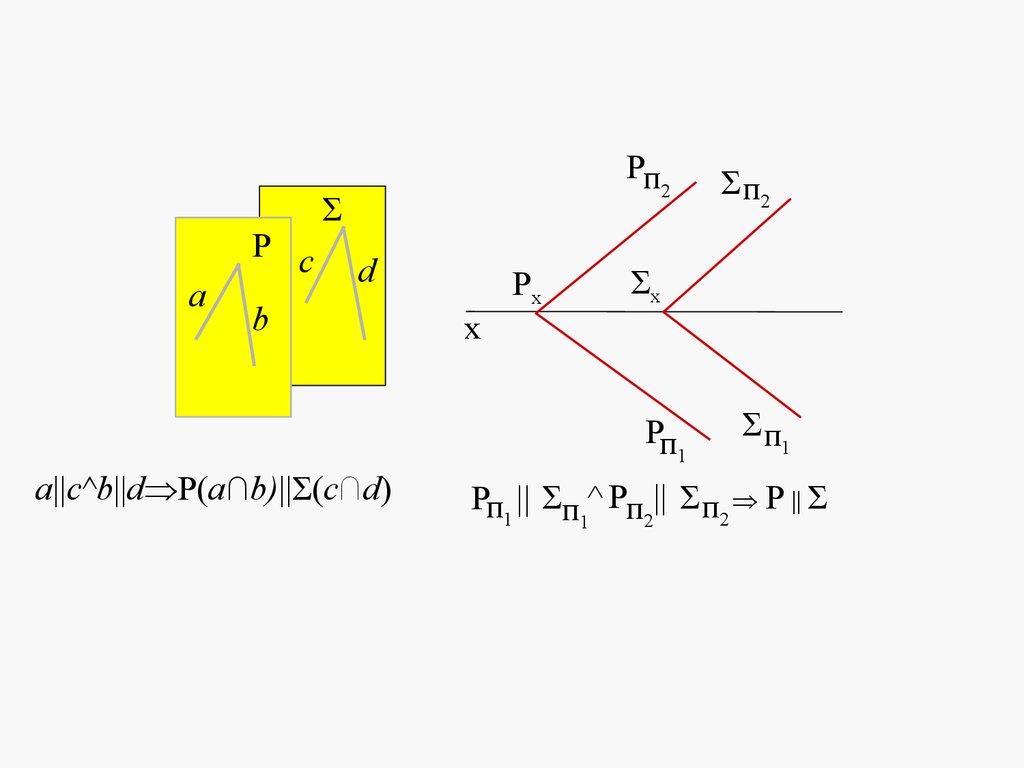
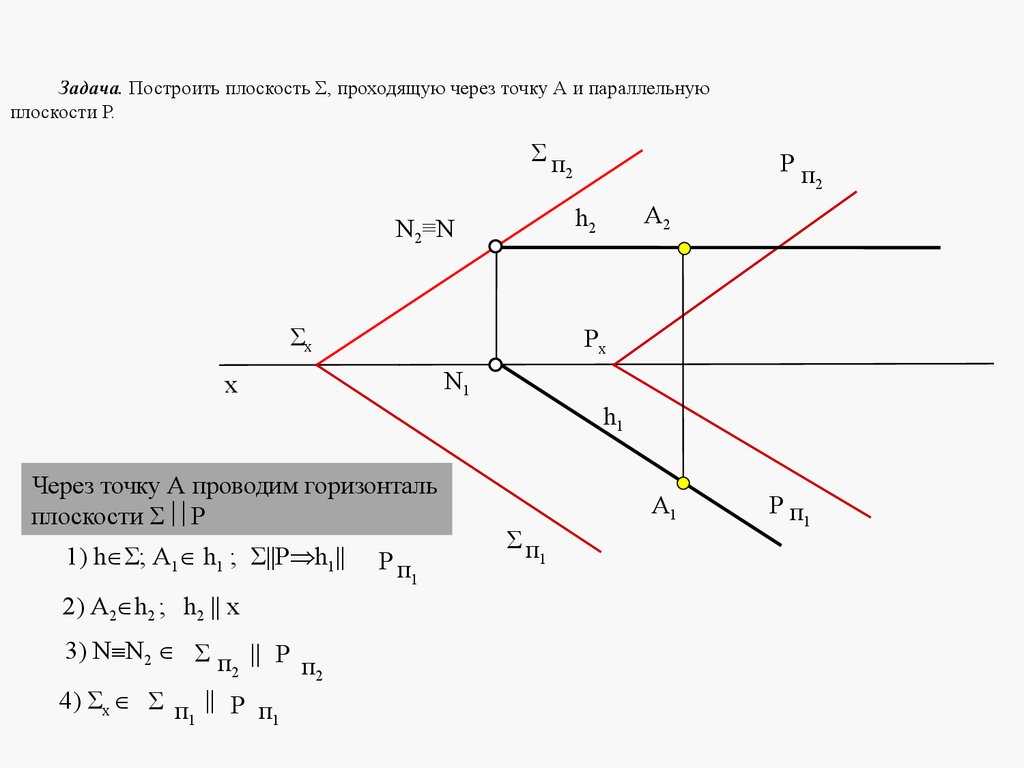
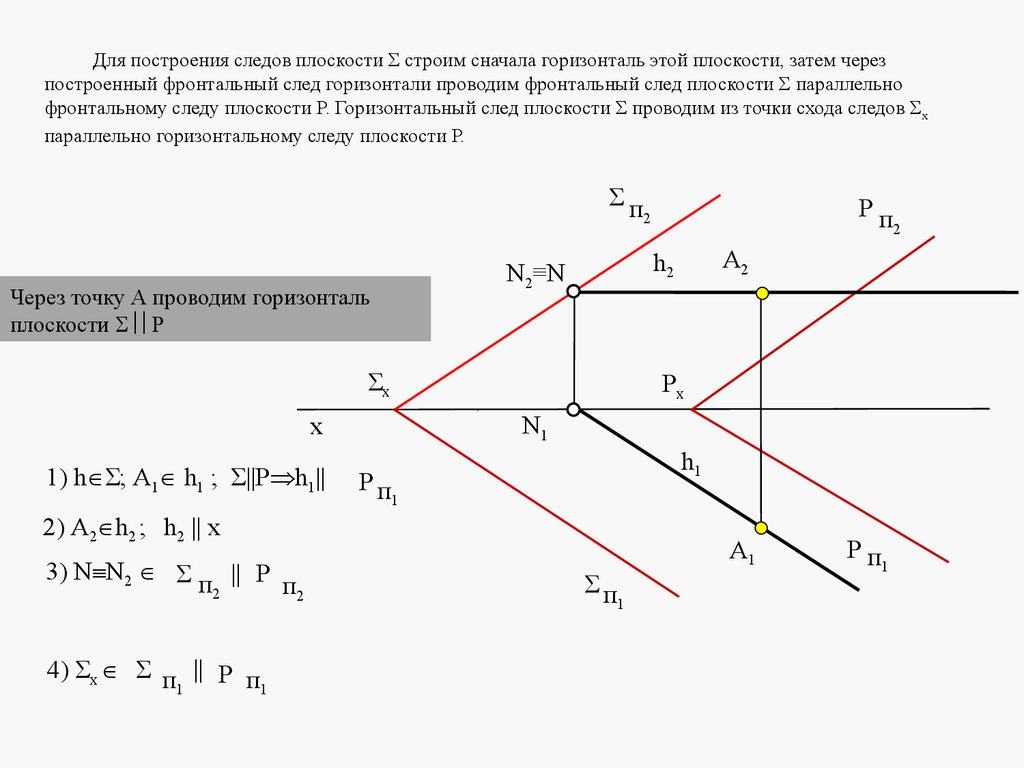
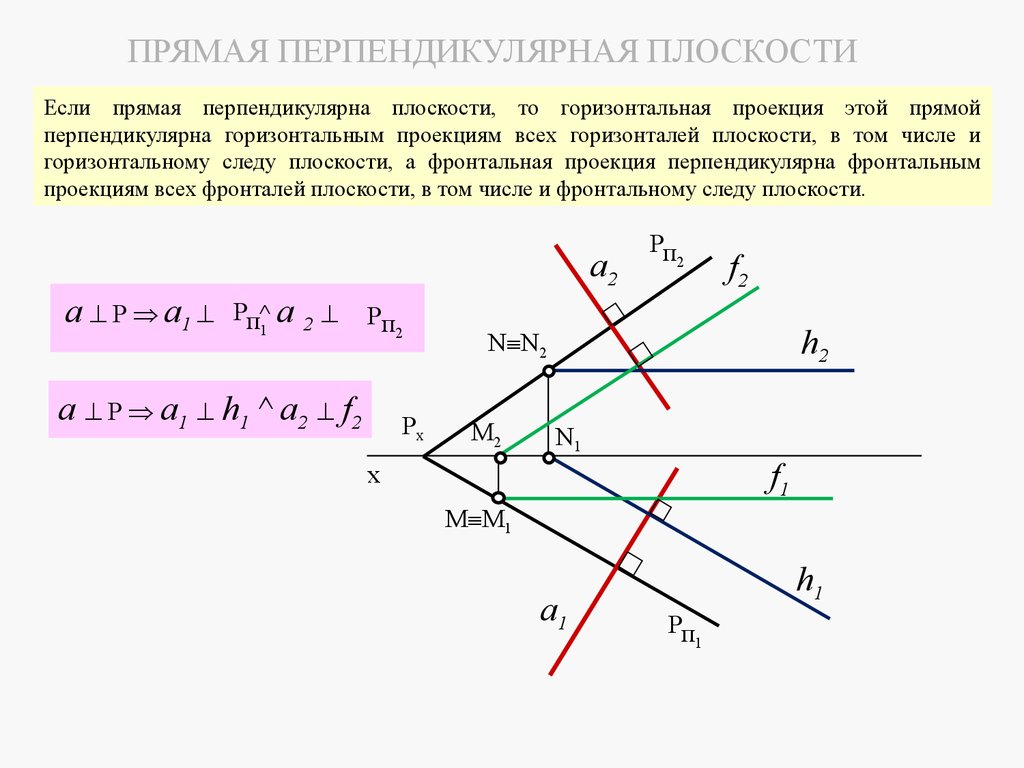
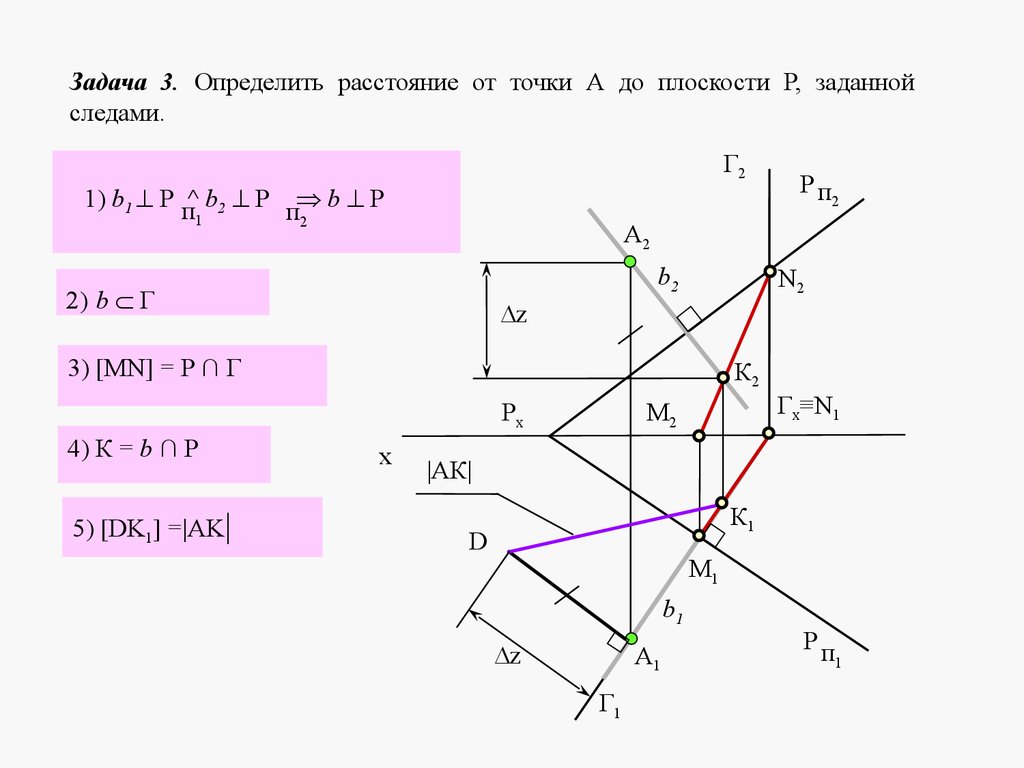
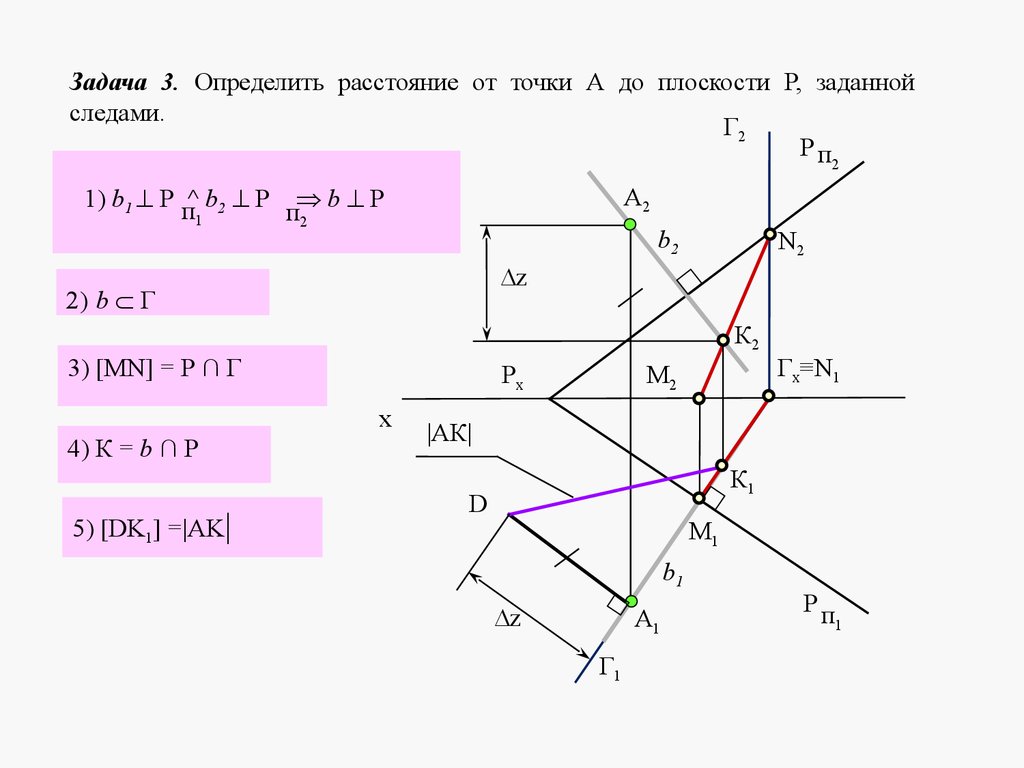
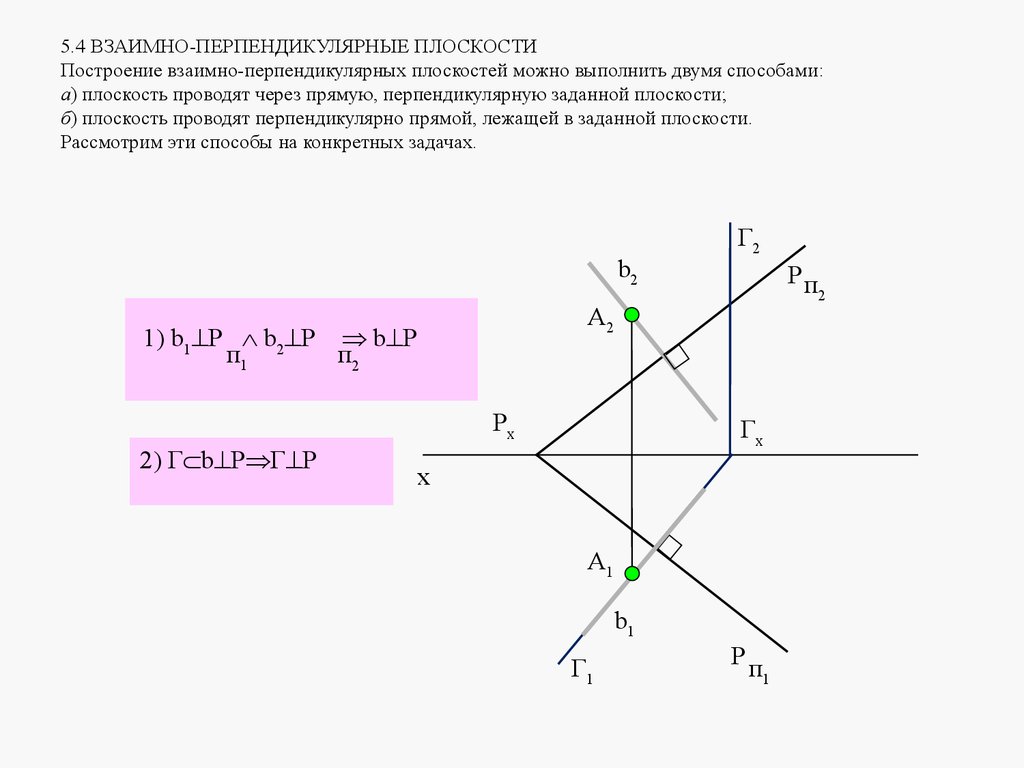
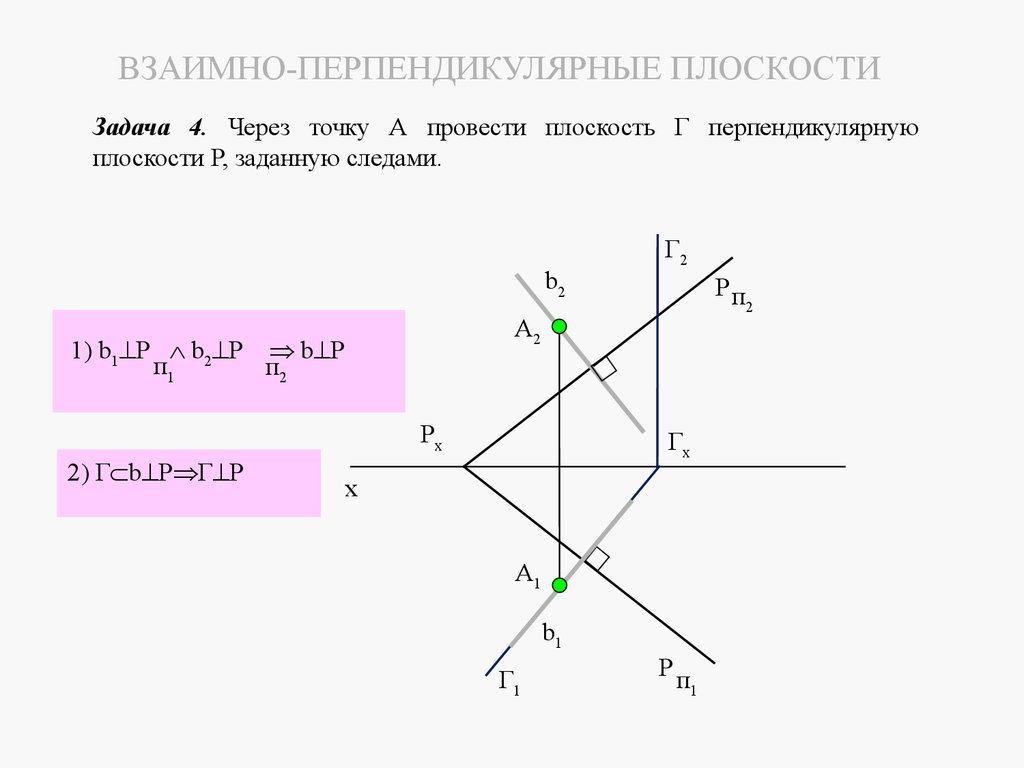
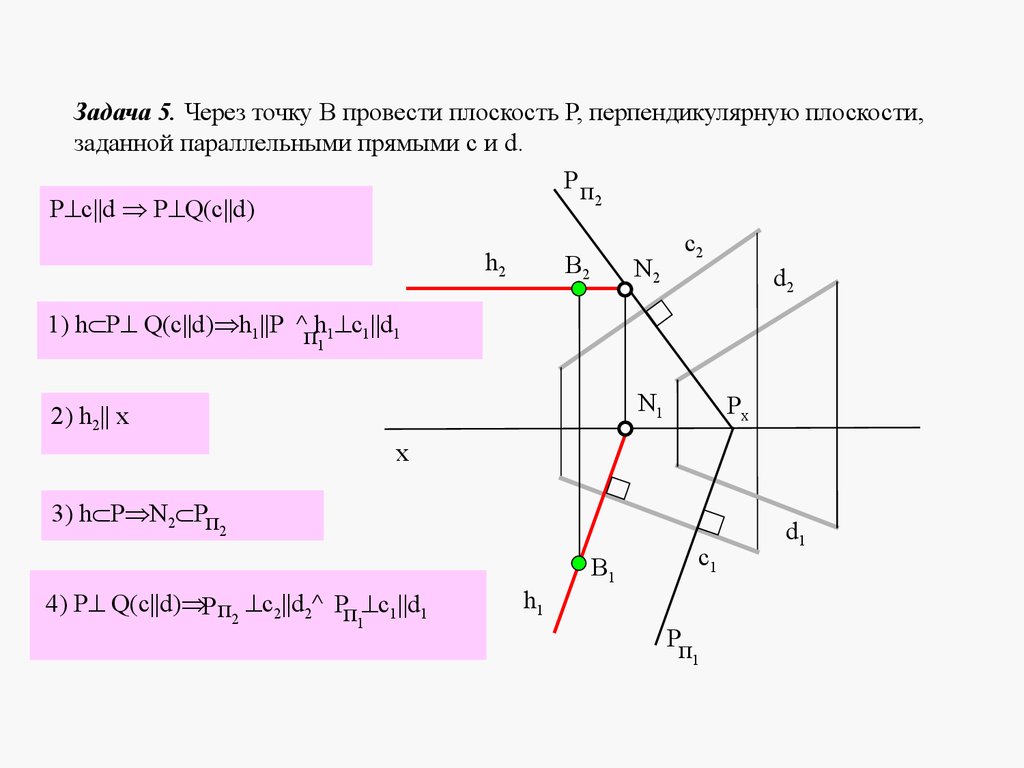
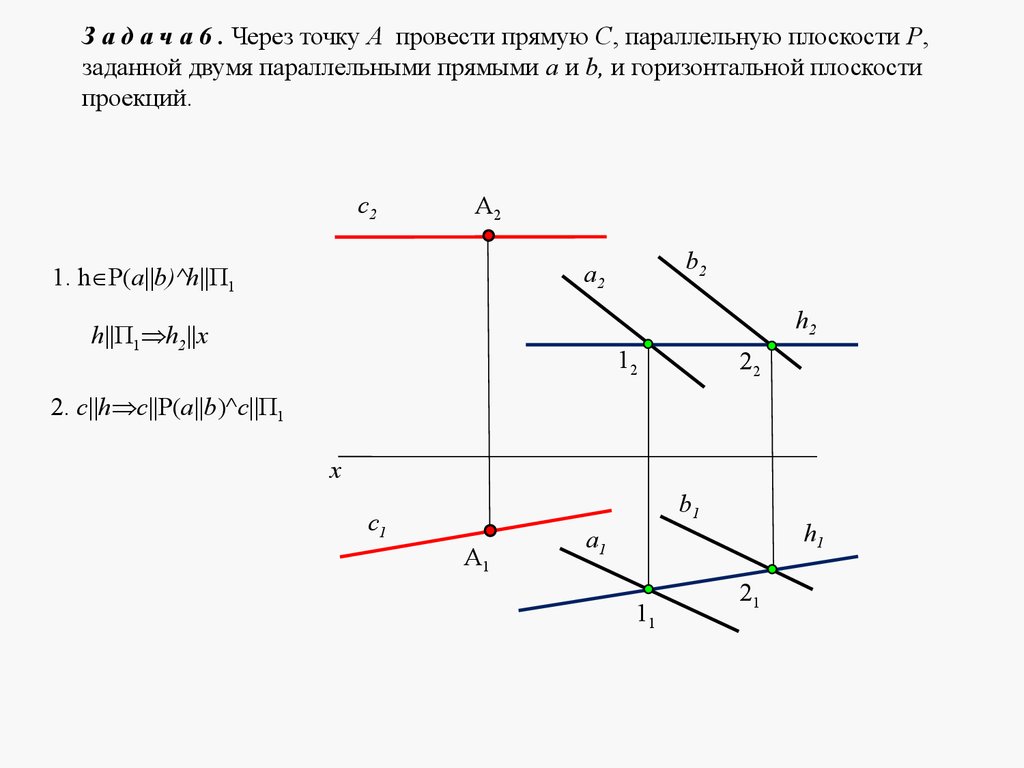
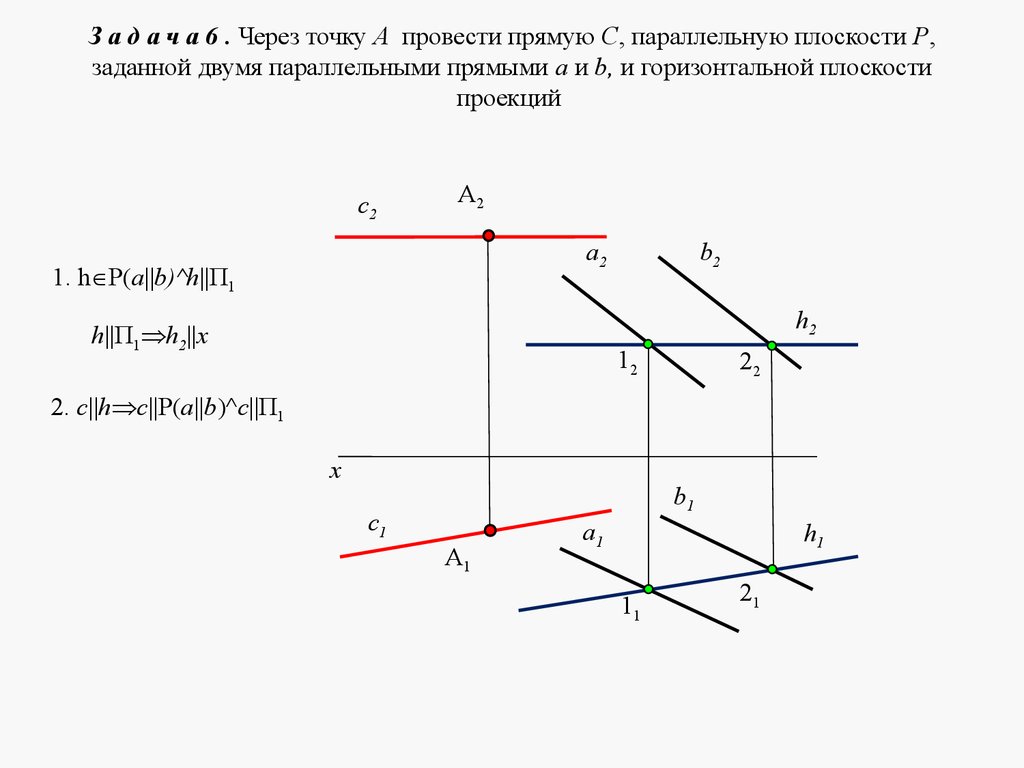
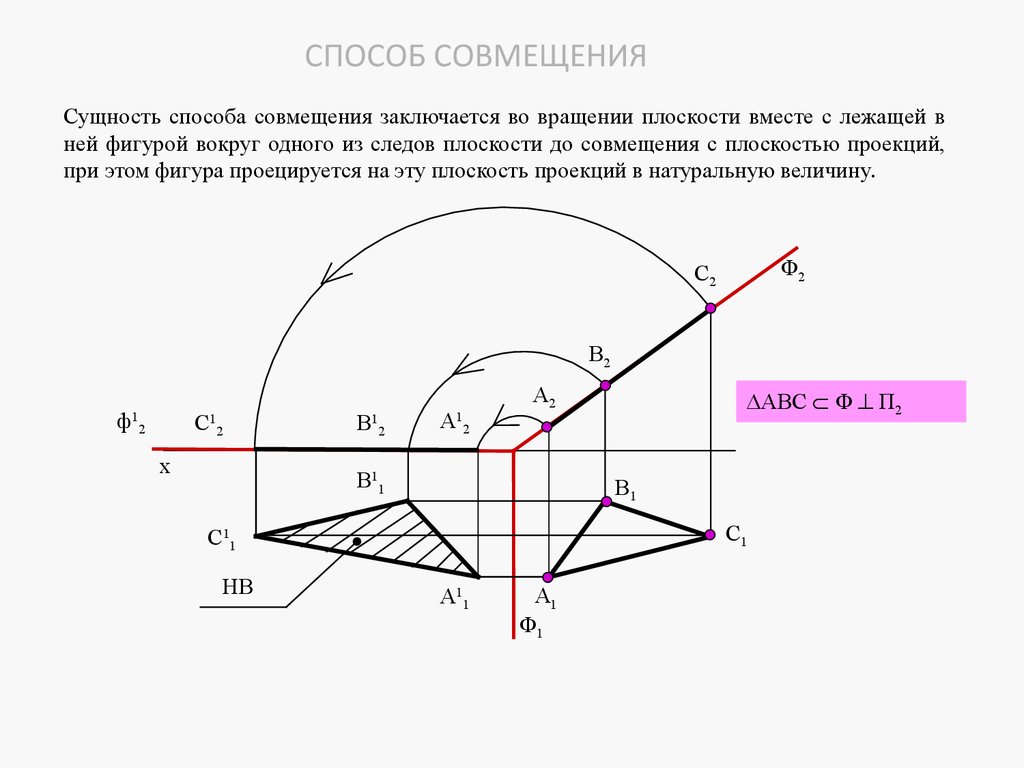
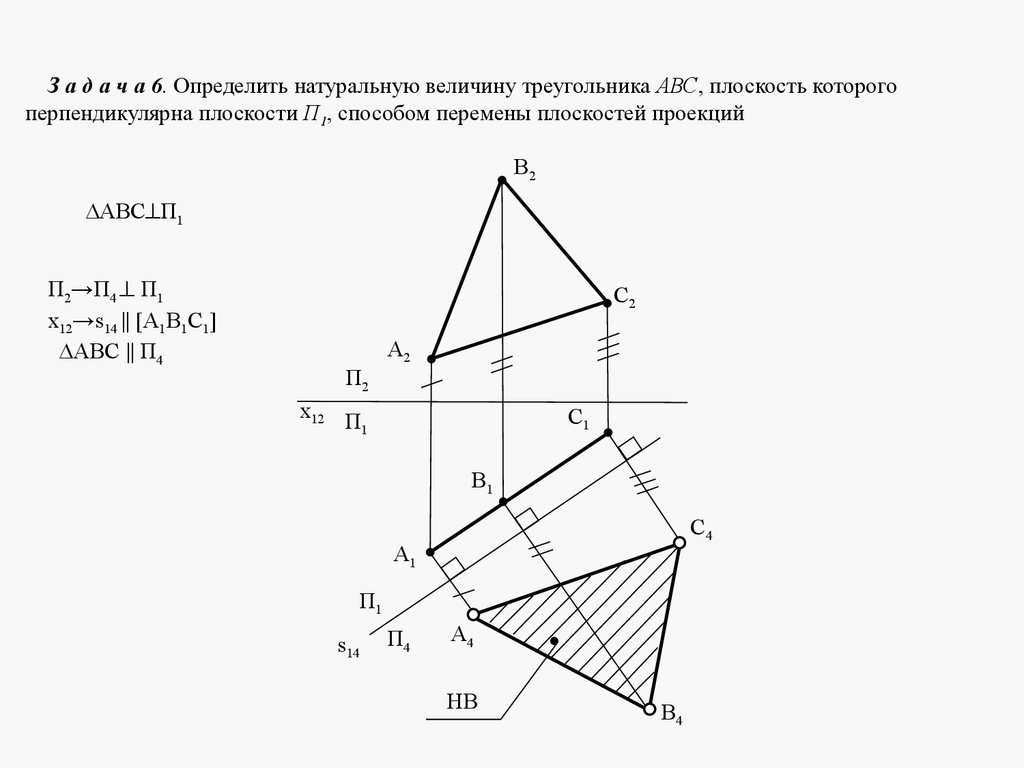
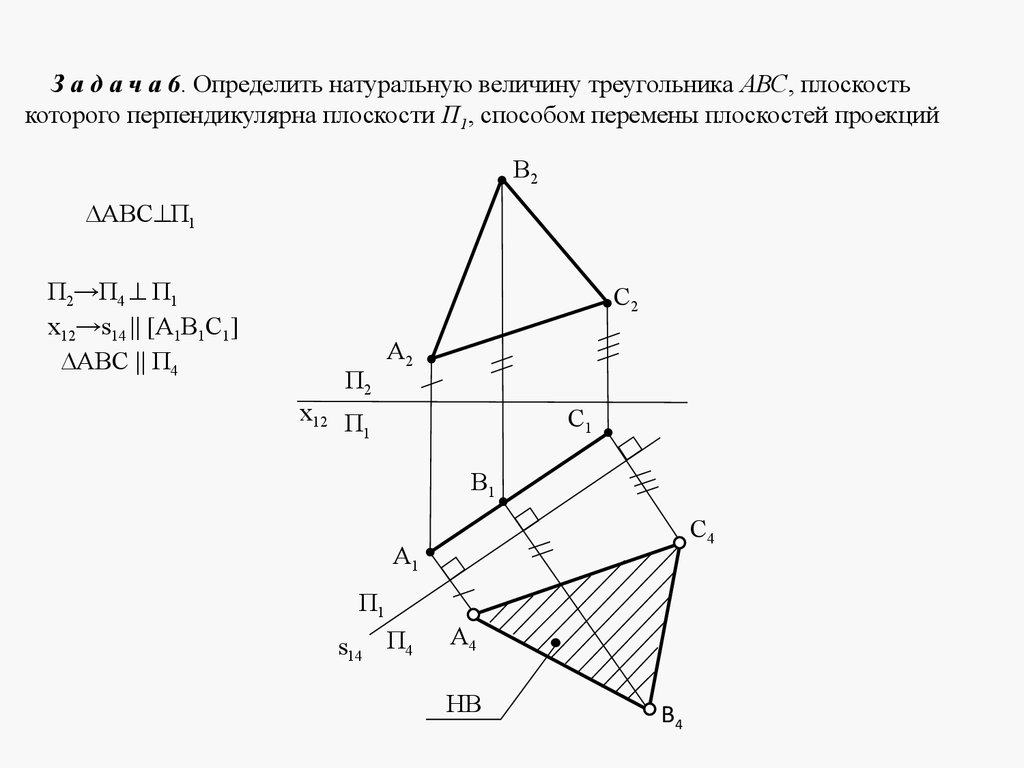
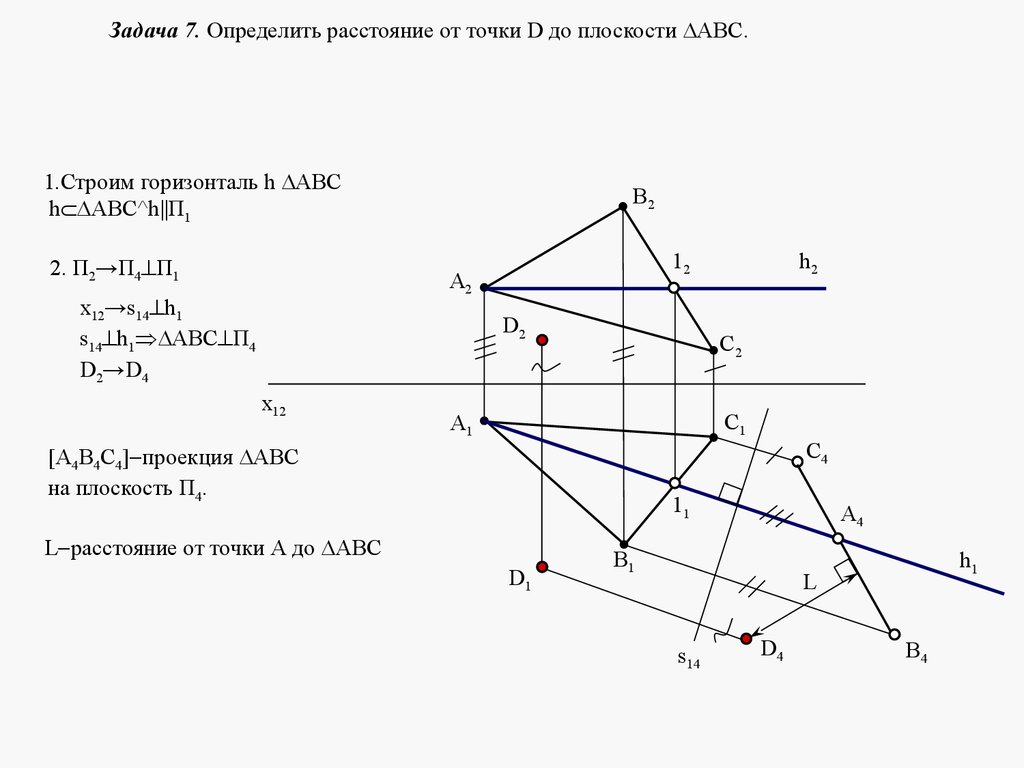
5. ЛЕКЦИЯ № 4. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ, ПРЯМОЙ ИПЛОСКОСТИ.
Плоскости в пространстве могут быть параллельными или пересека






























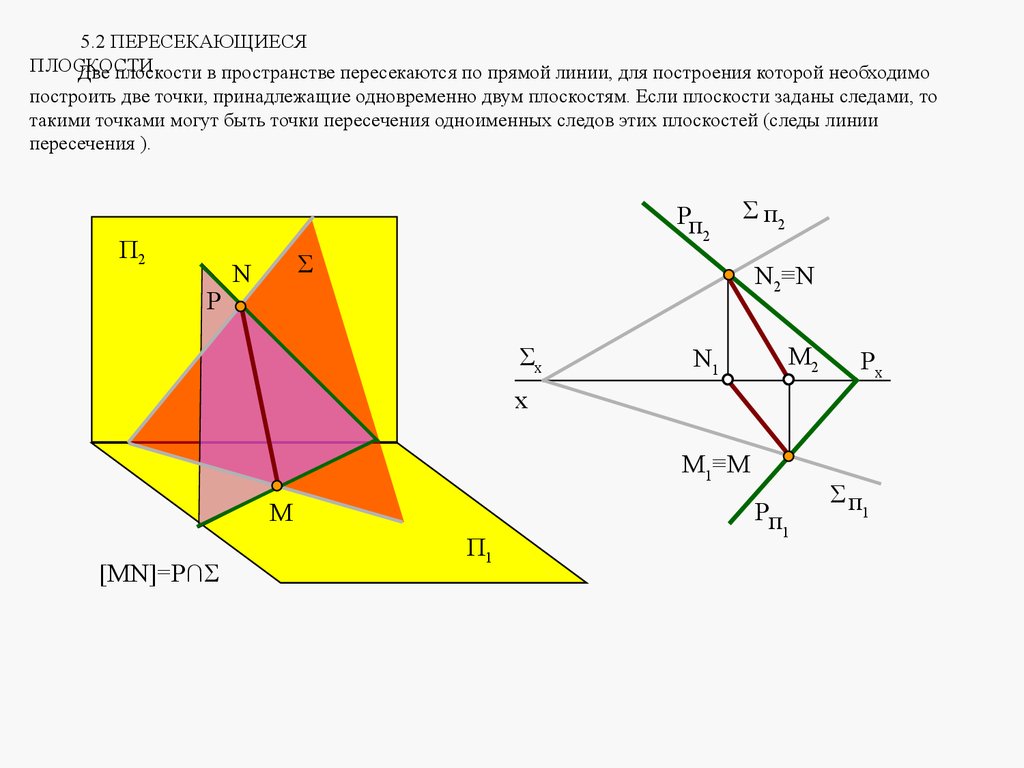
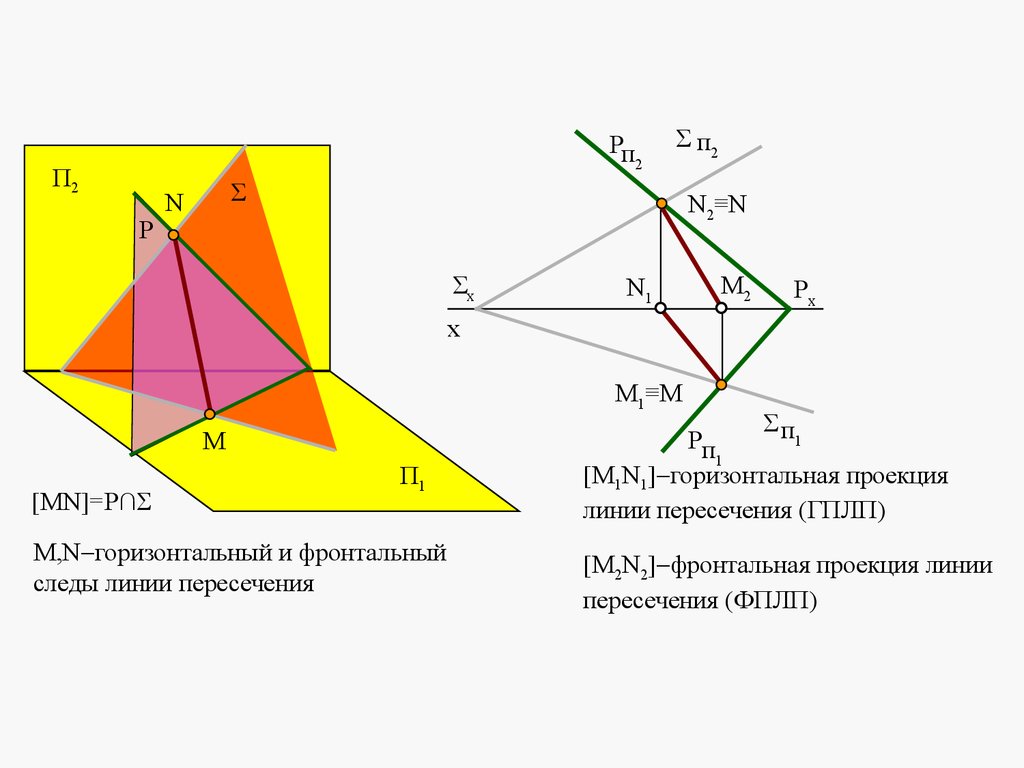
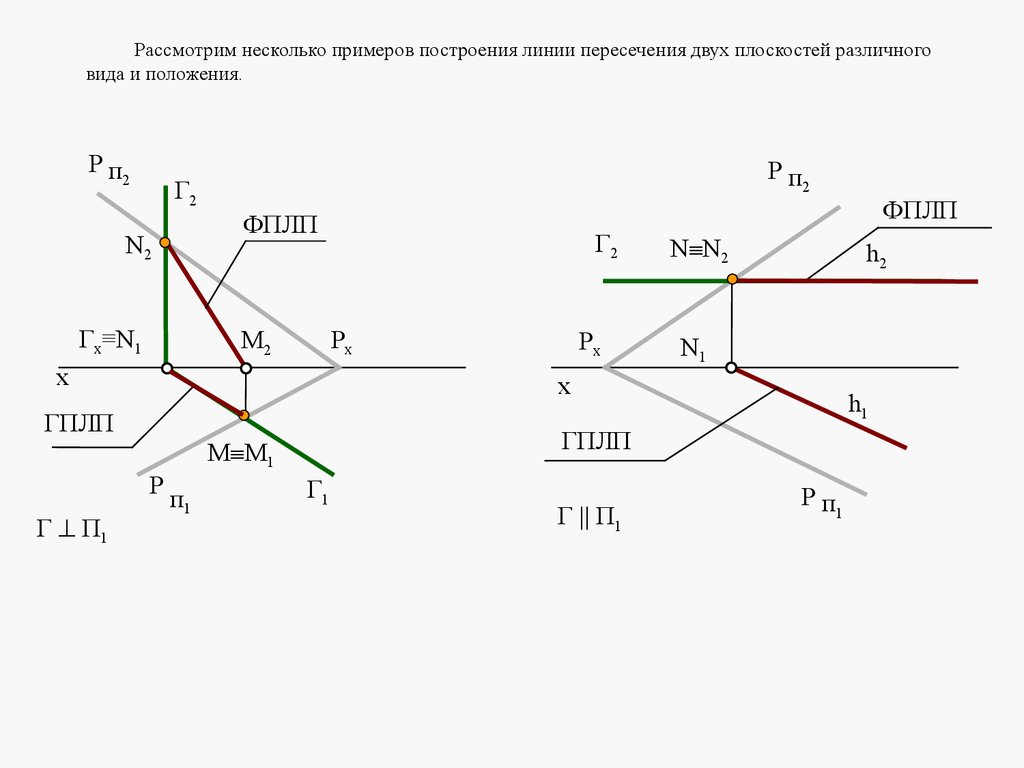
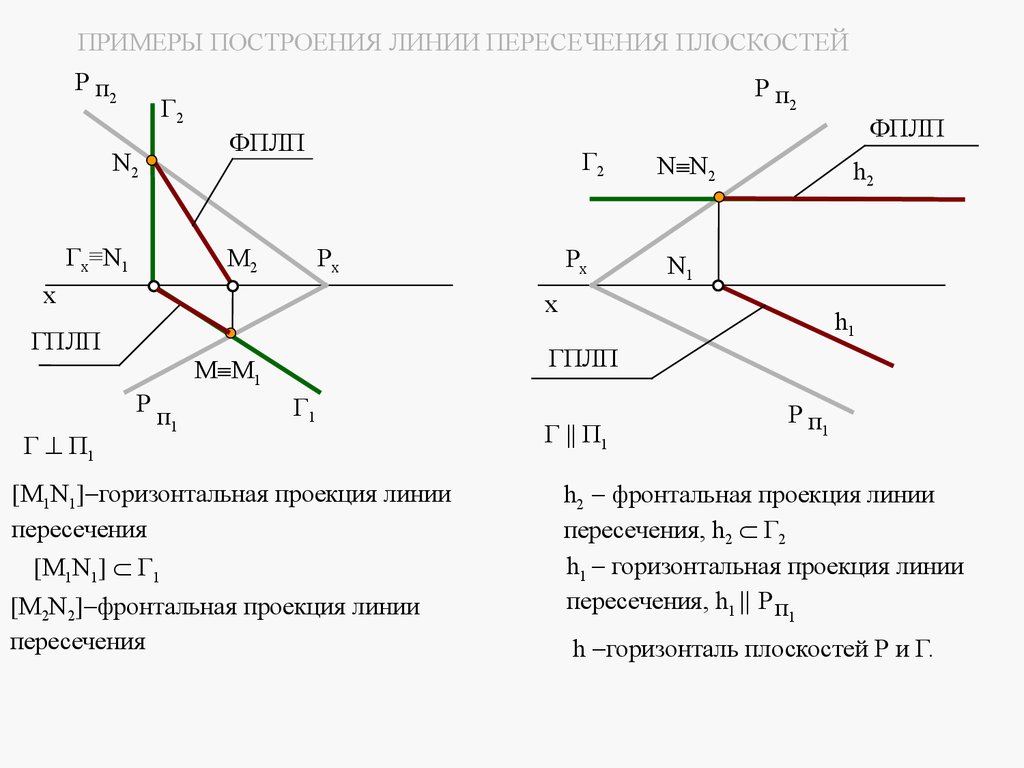
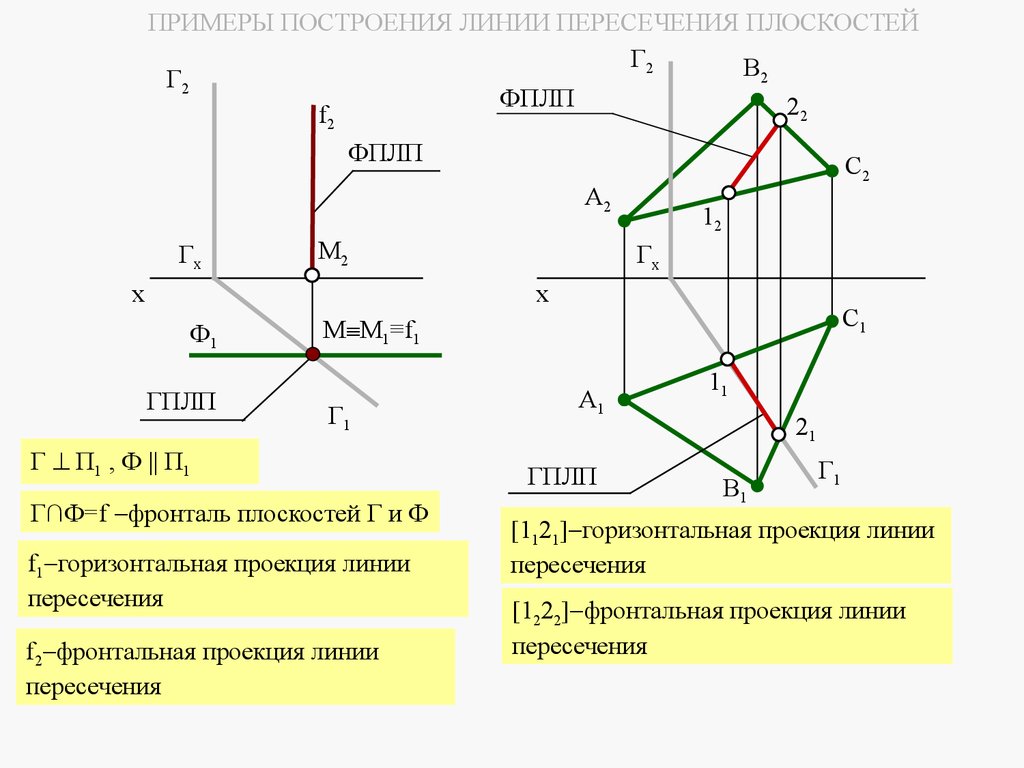
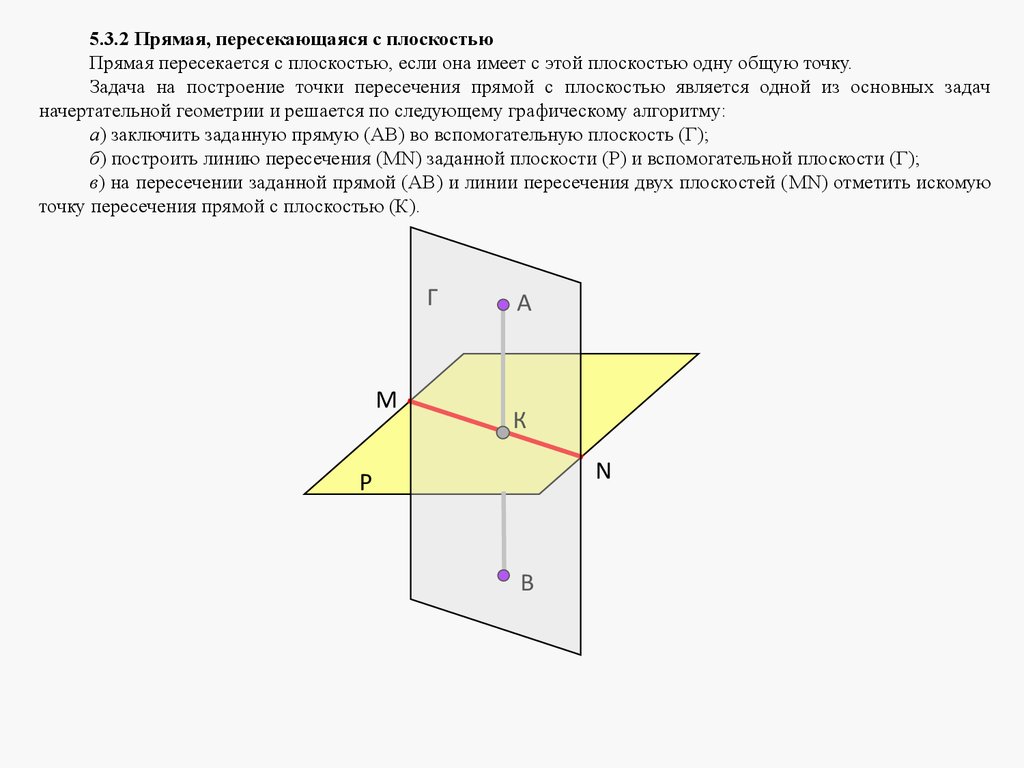
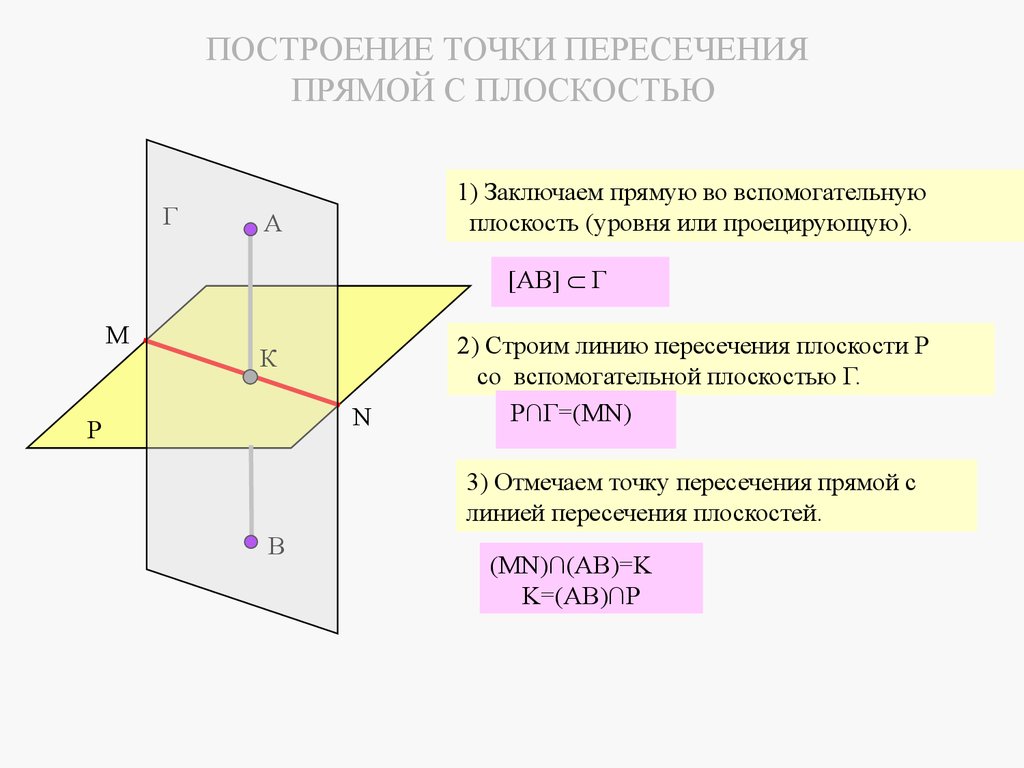
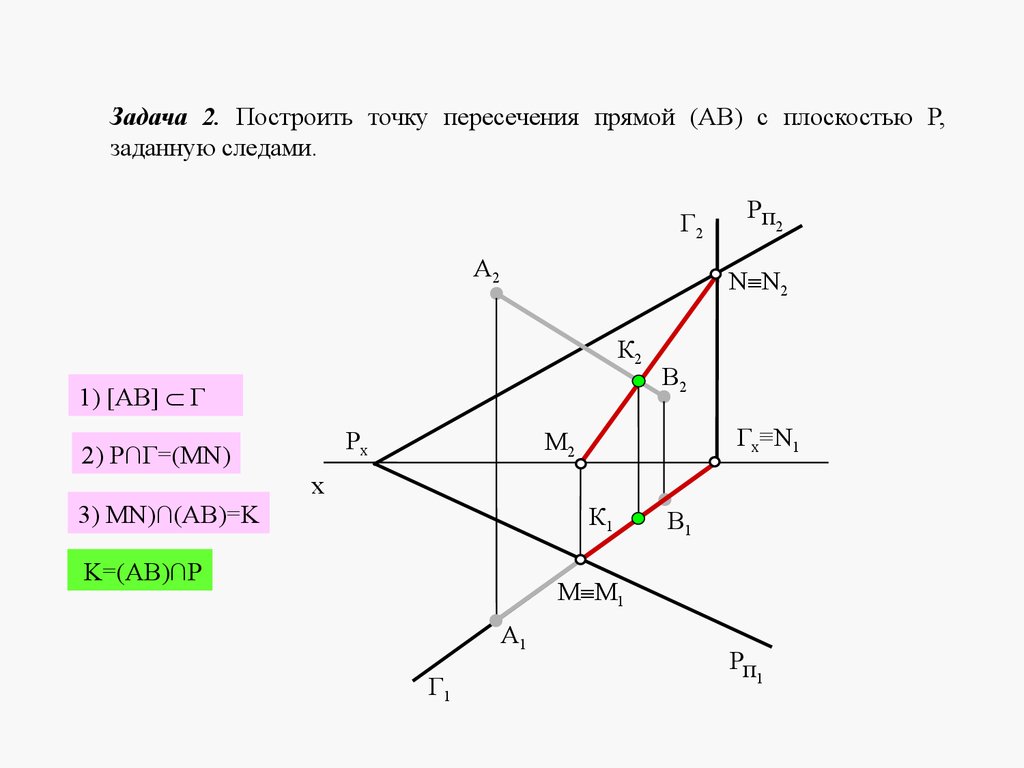
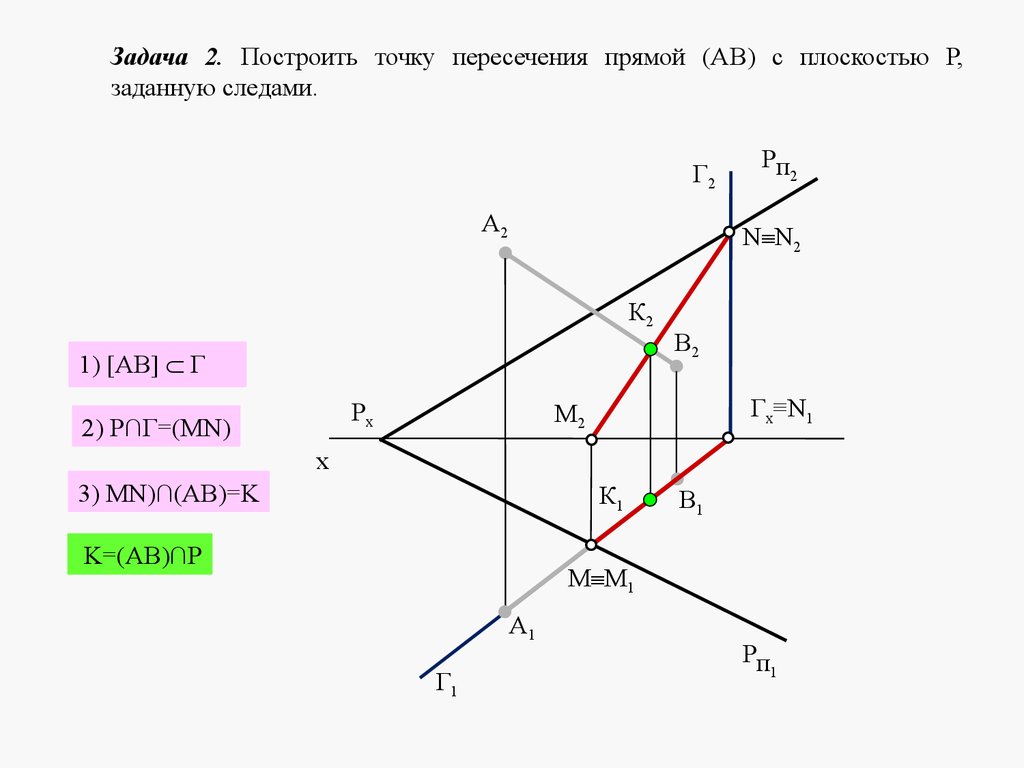
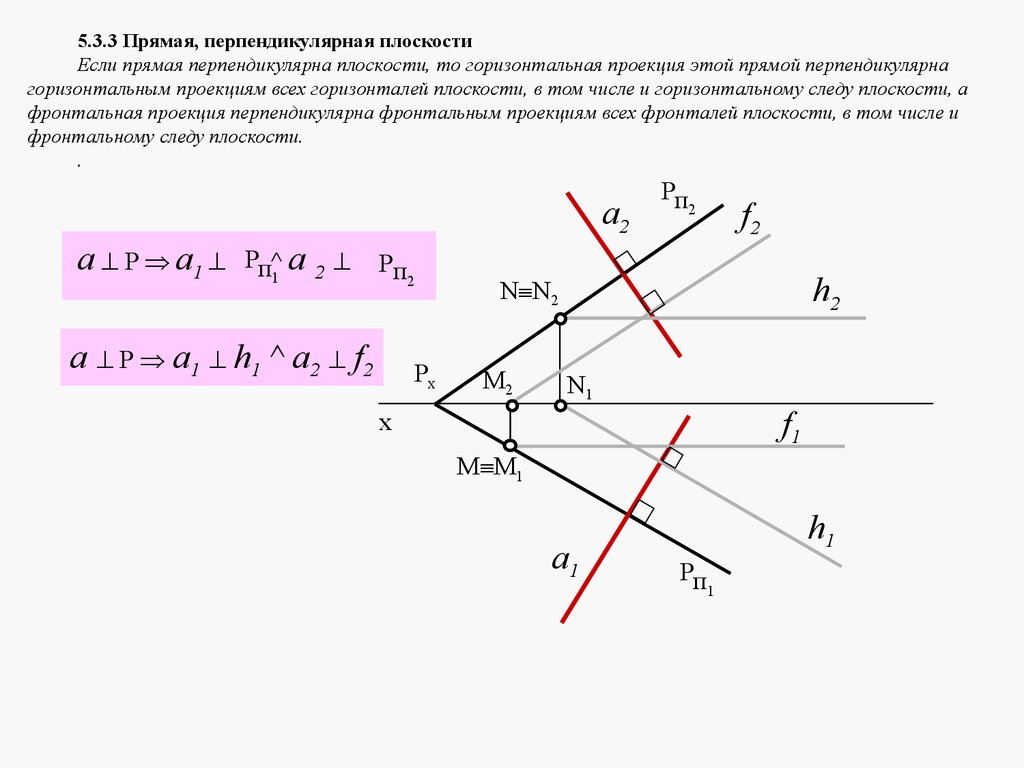
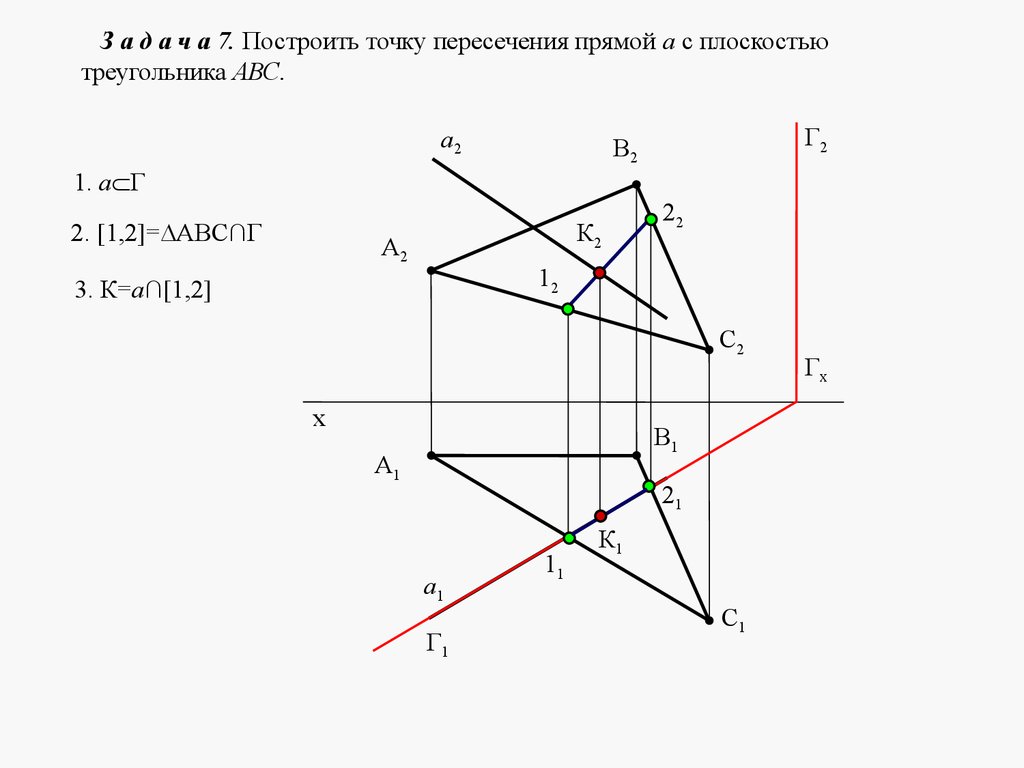
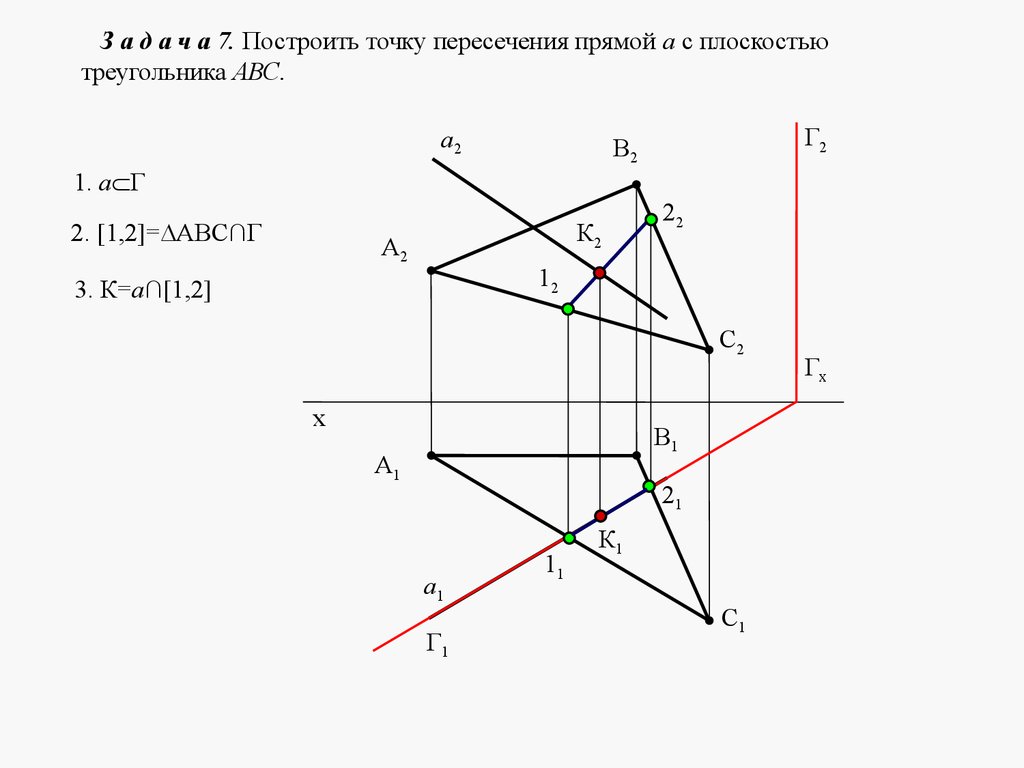
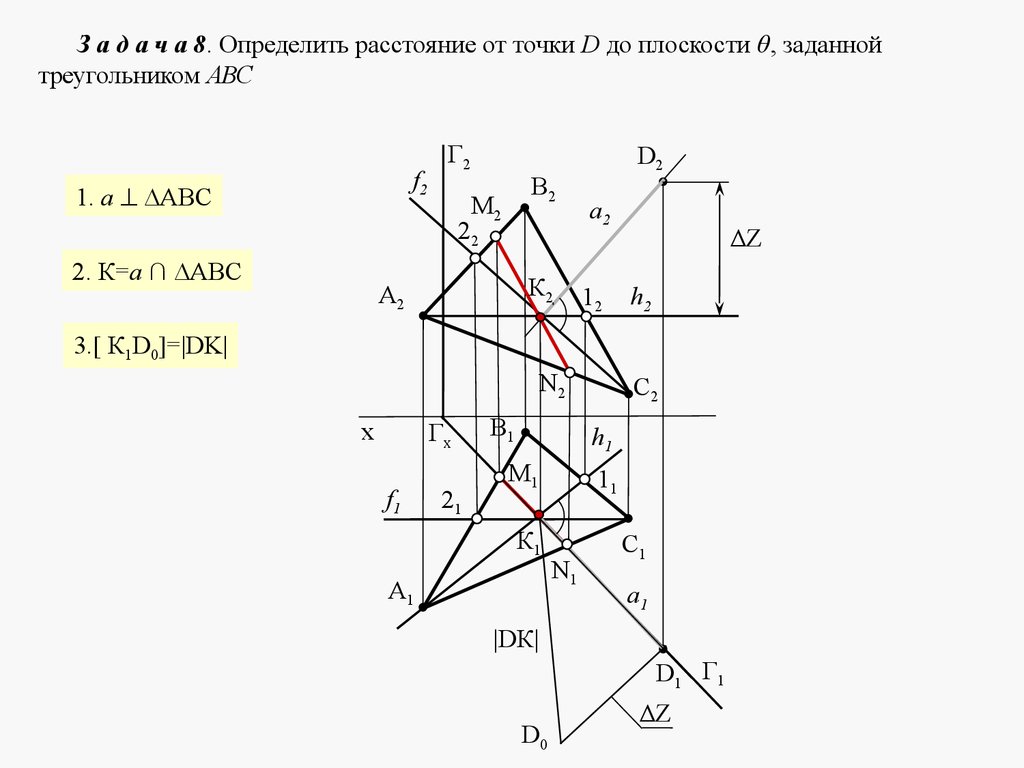

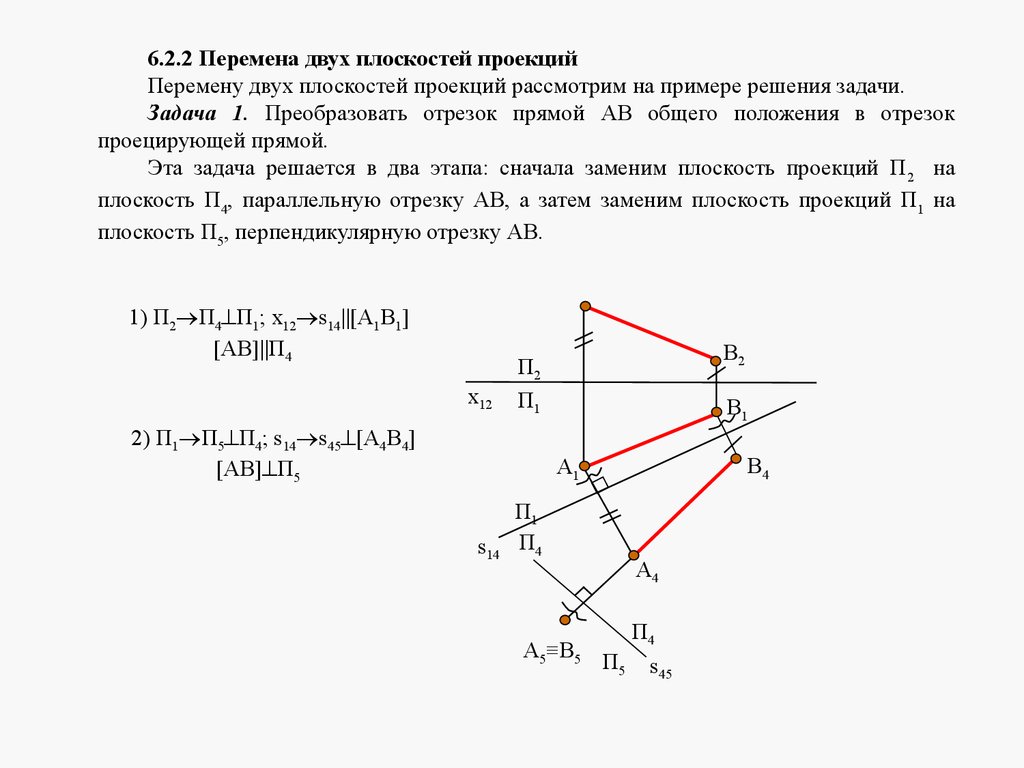
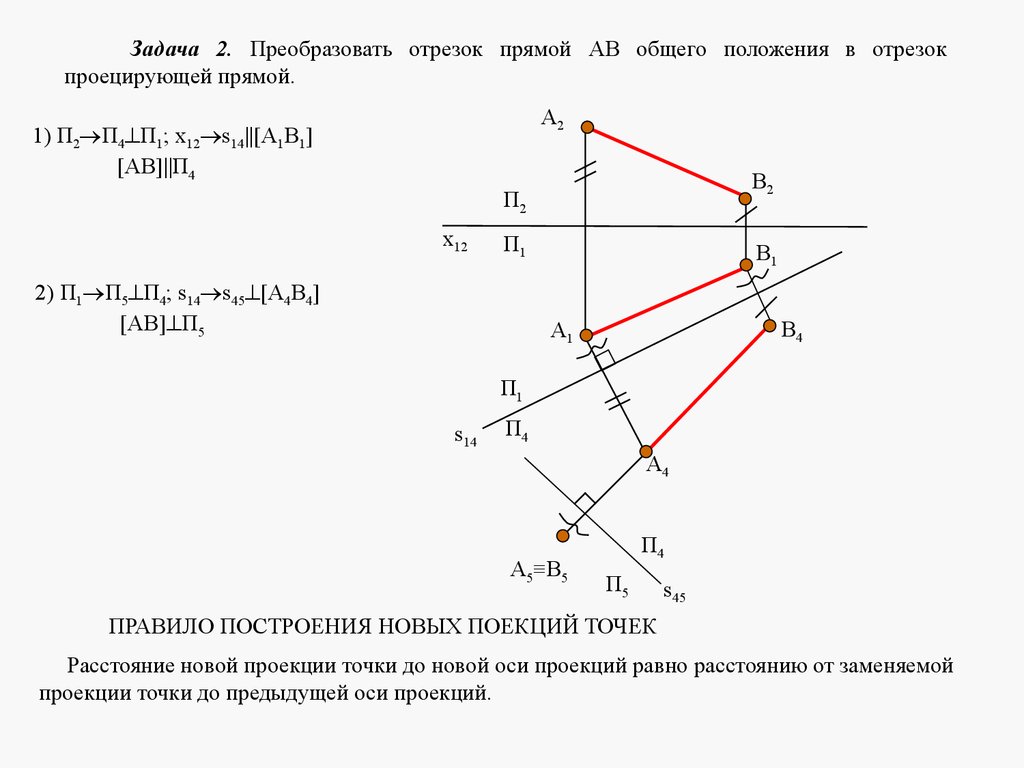
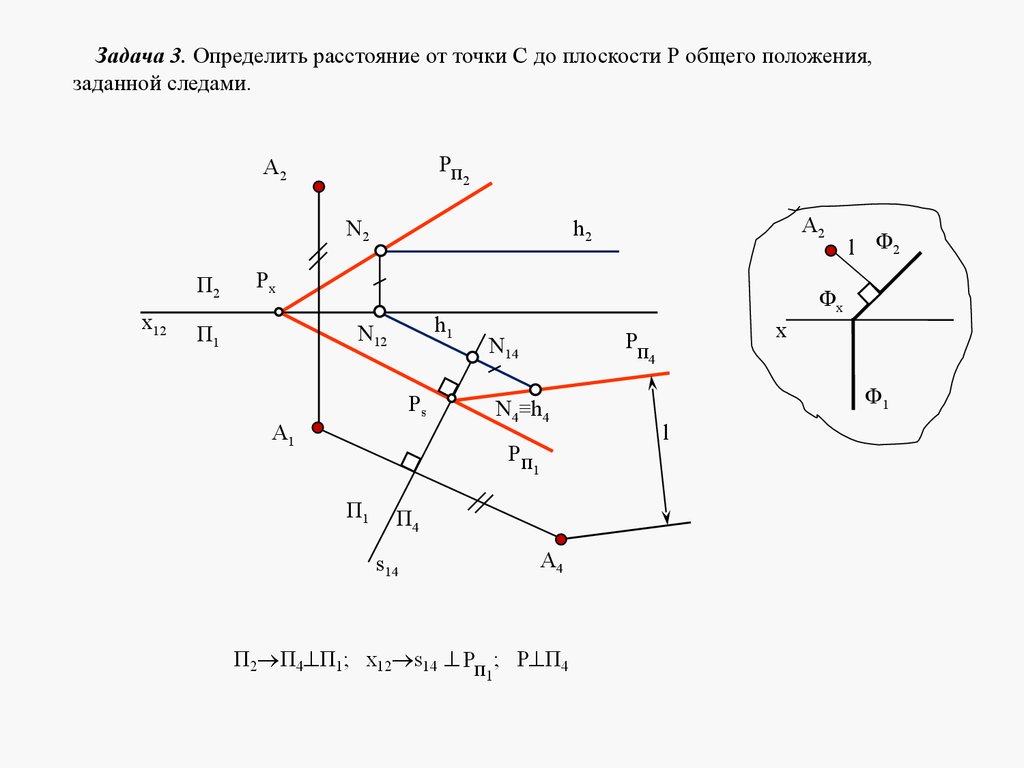
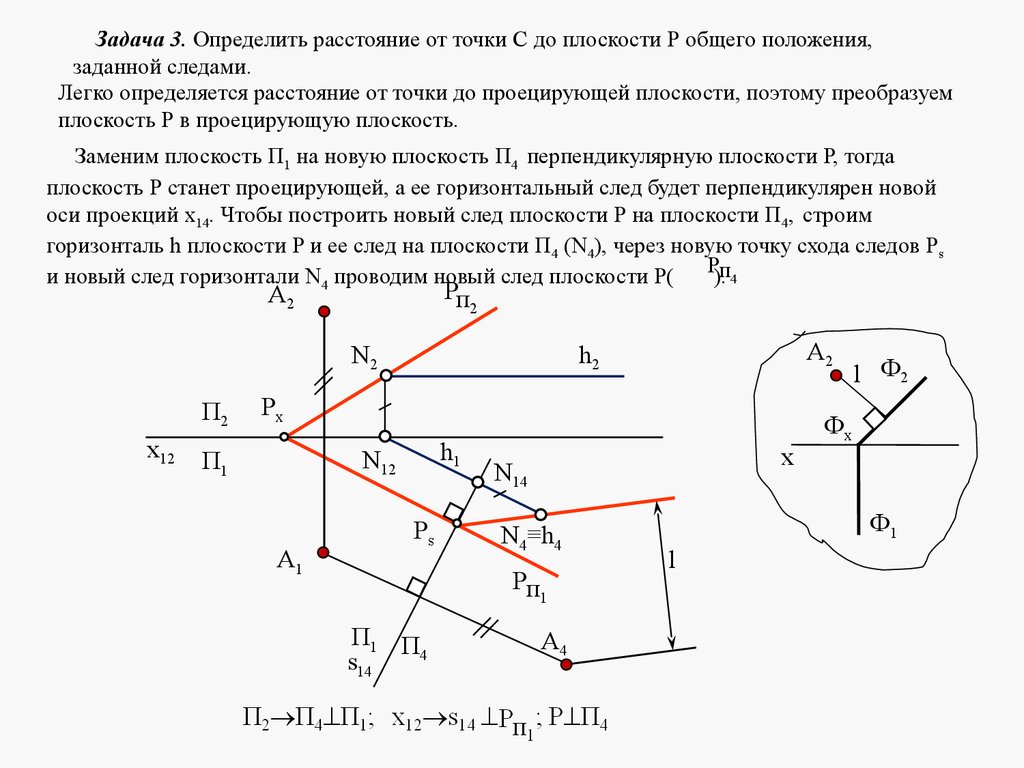

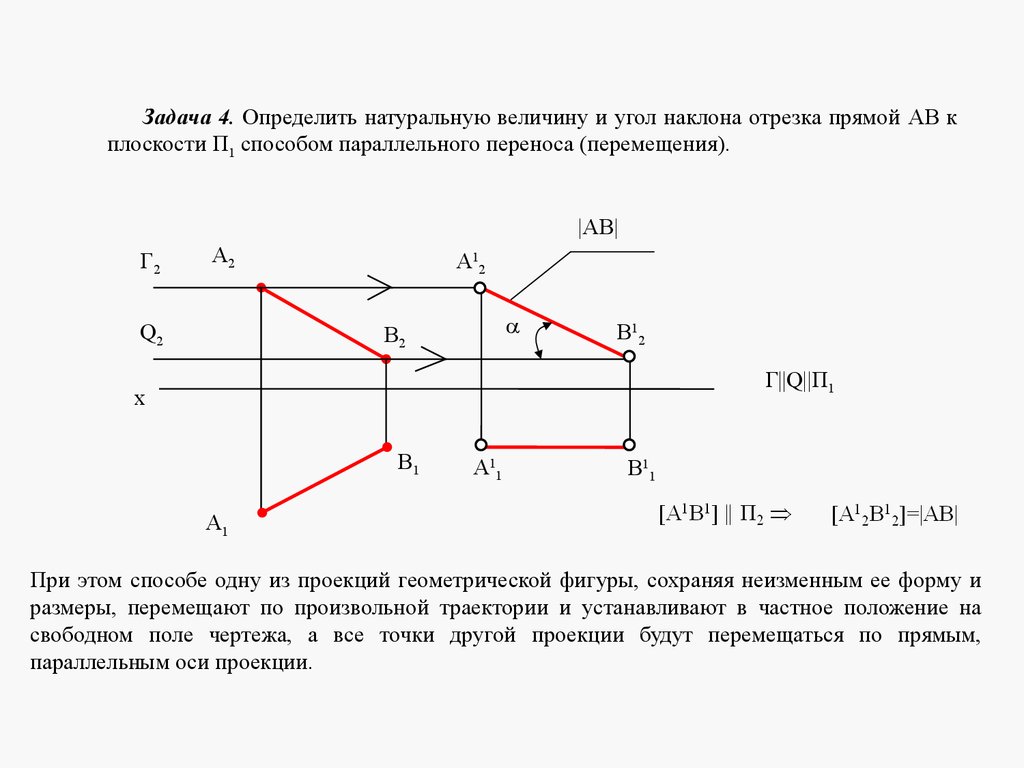

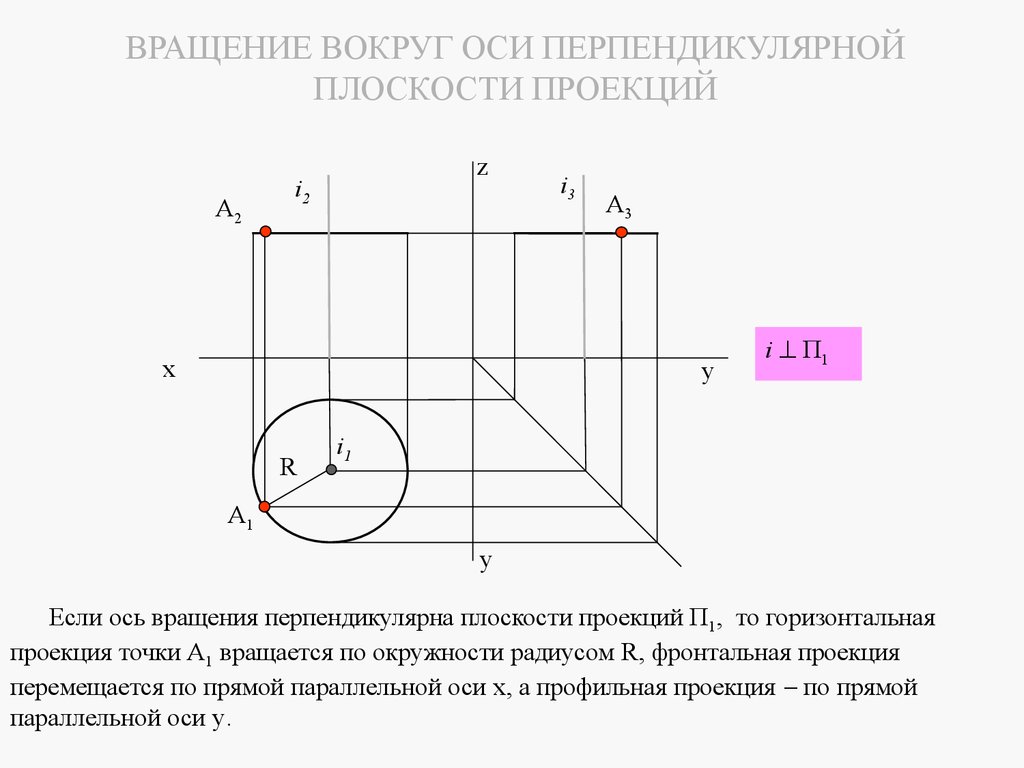

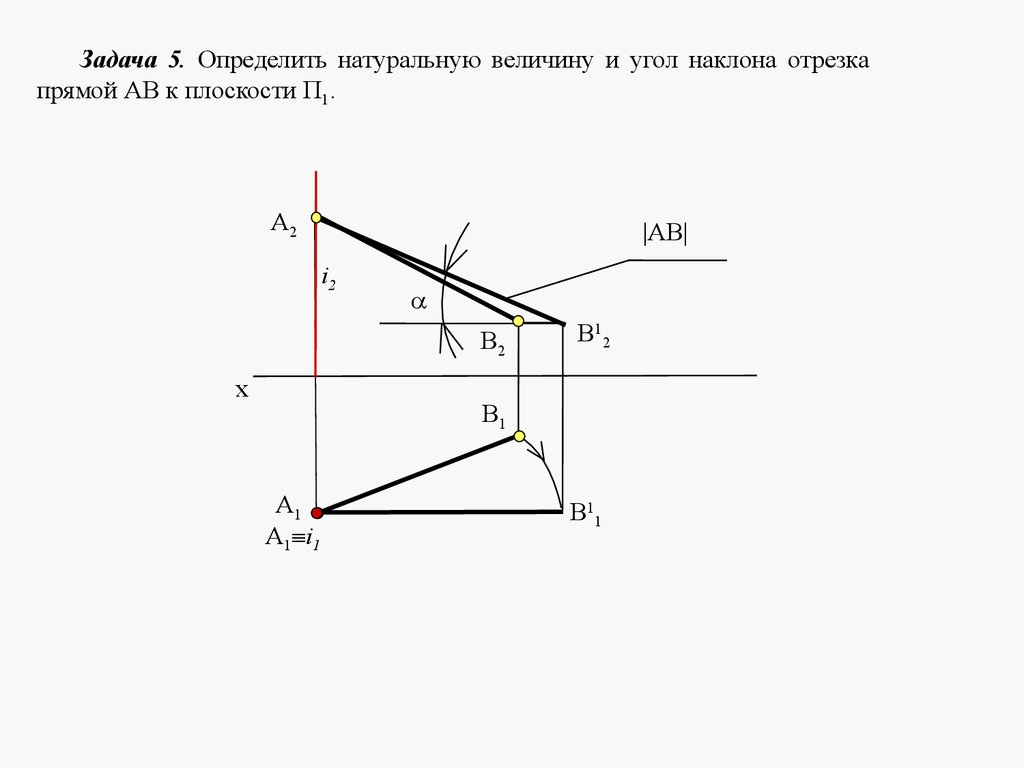
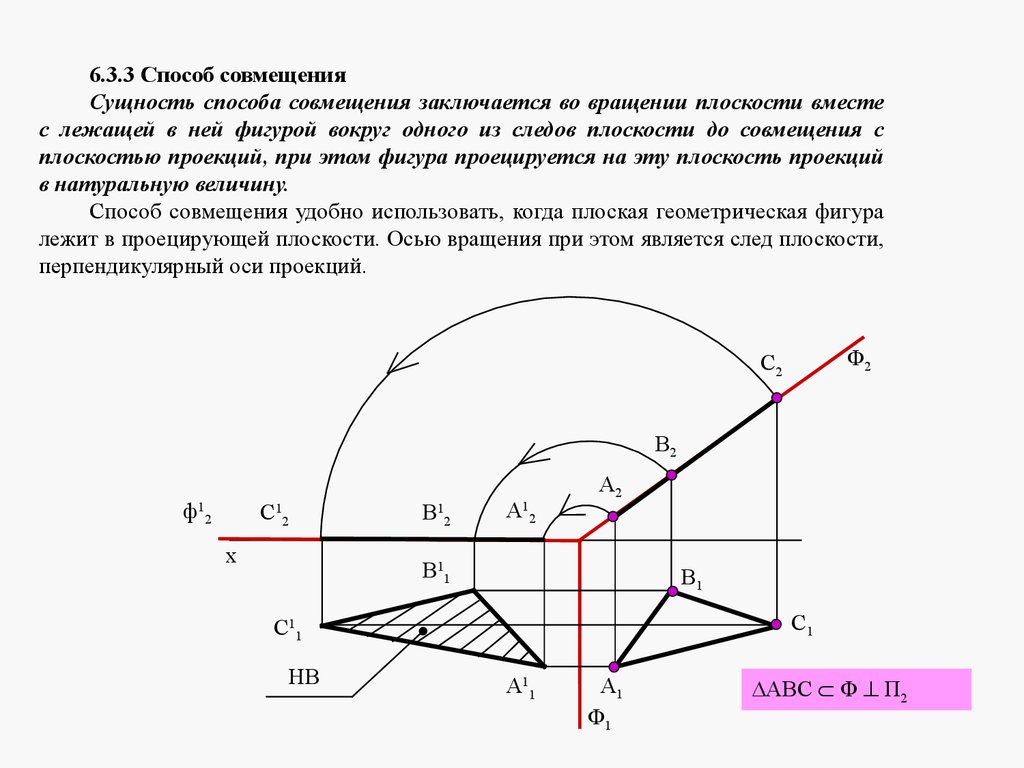

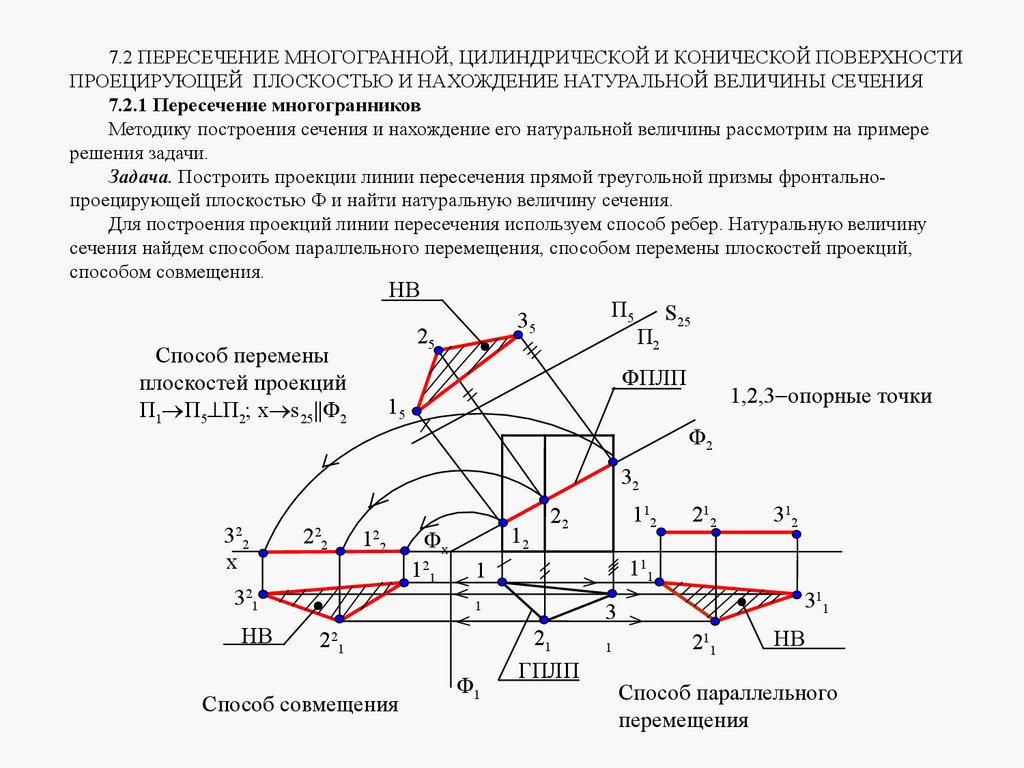
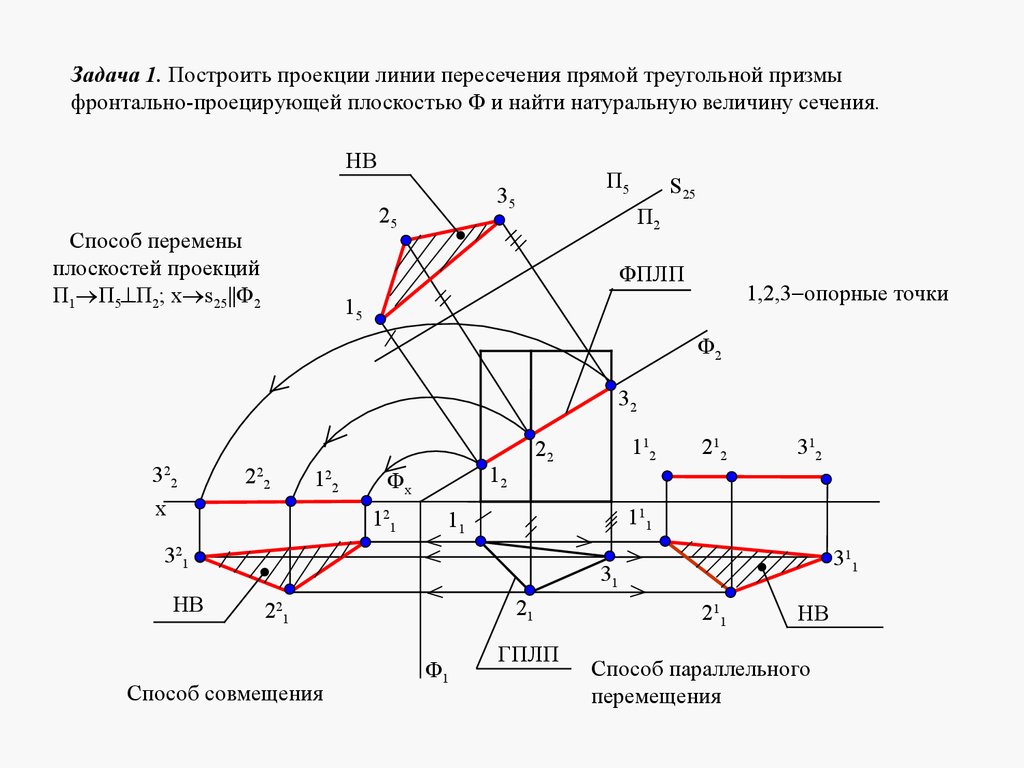
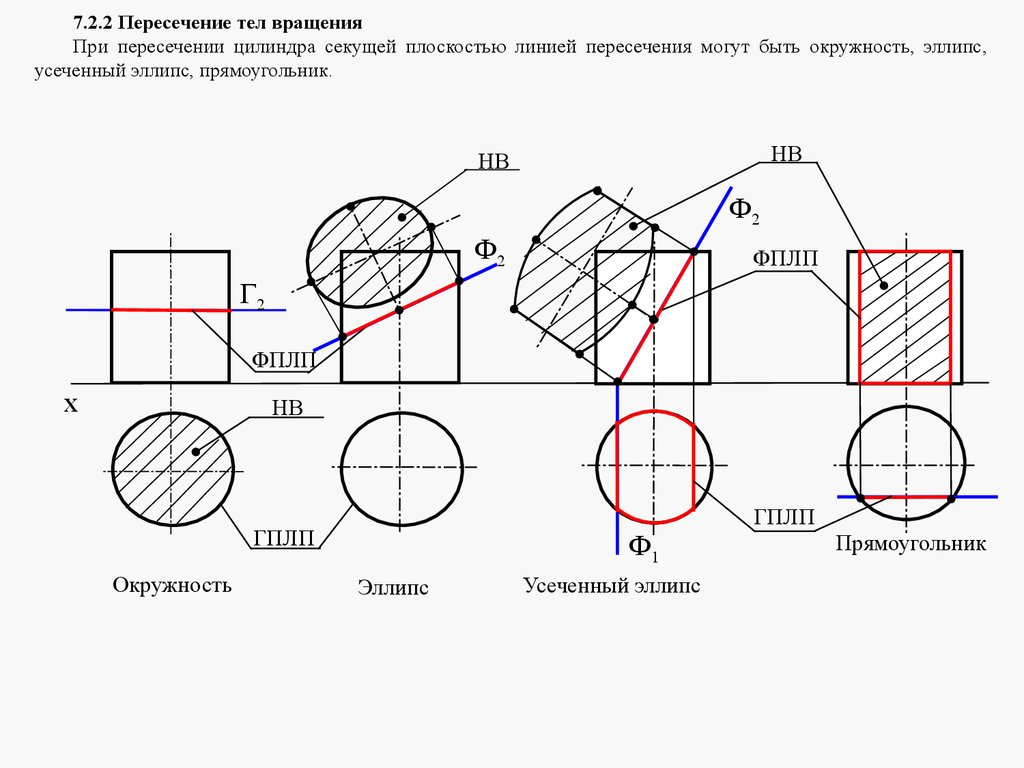
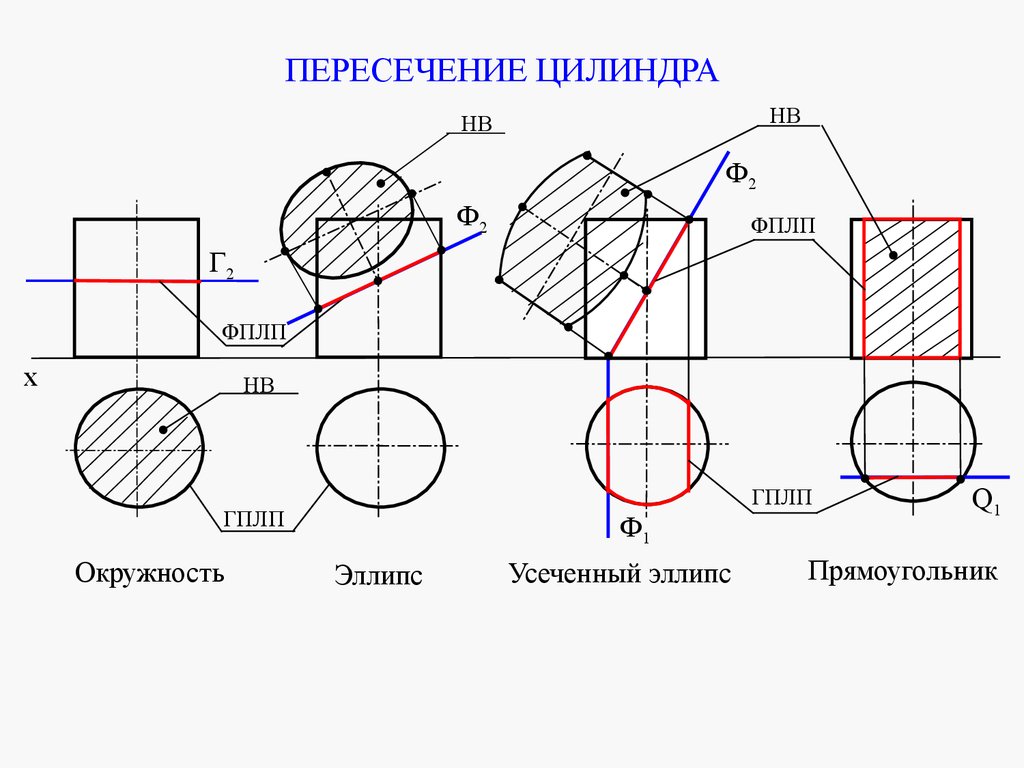
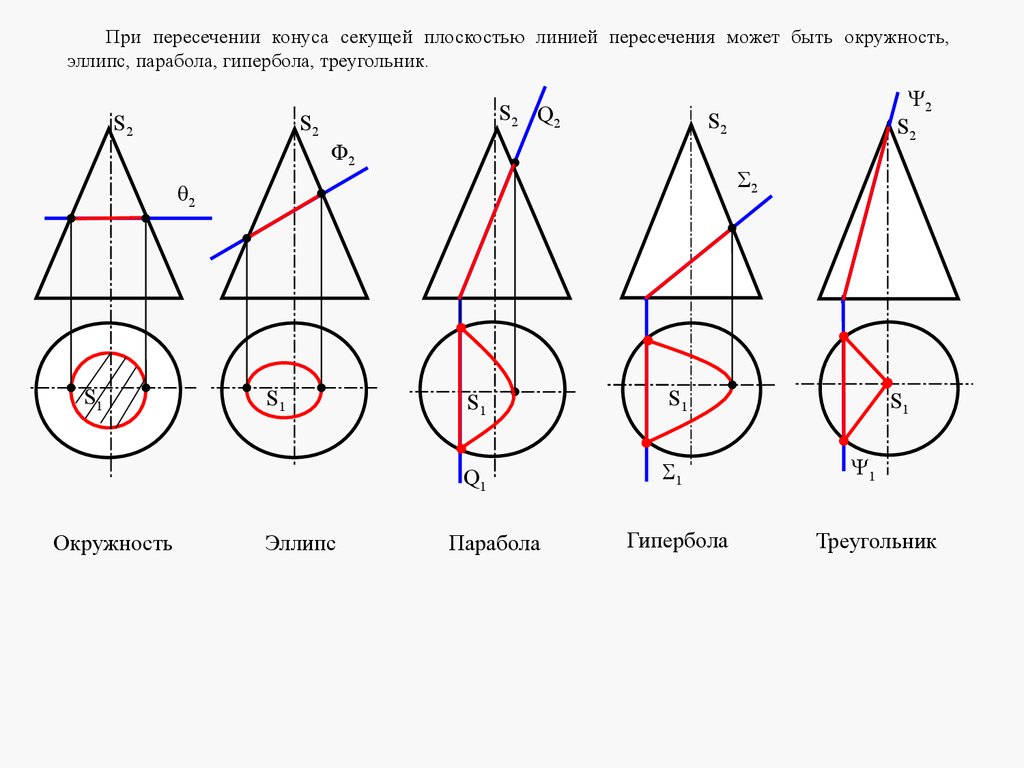
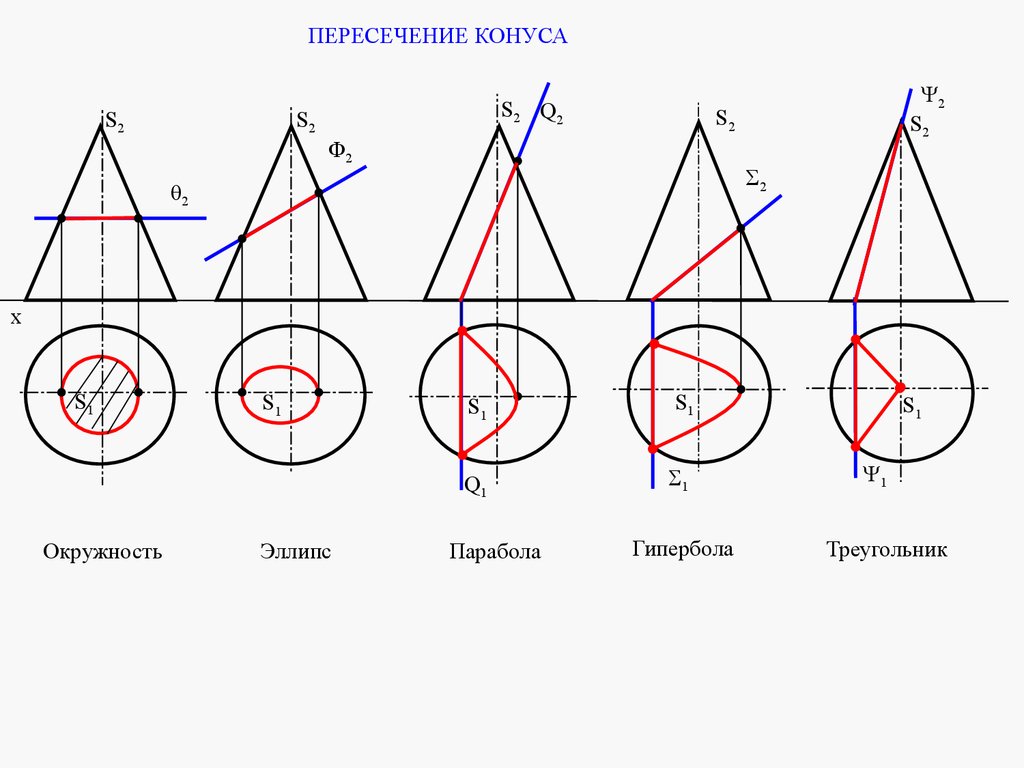
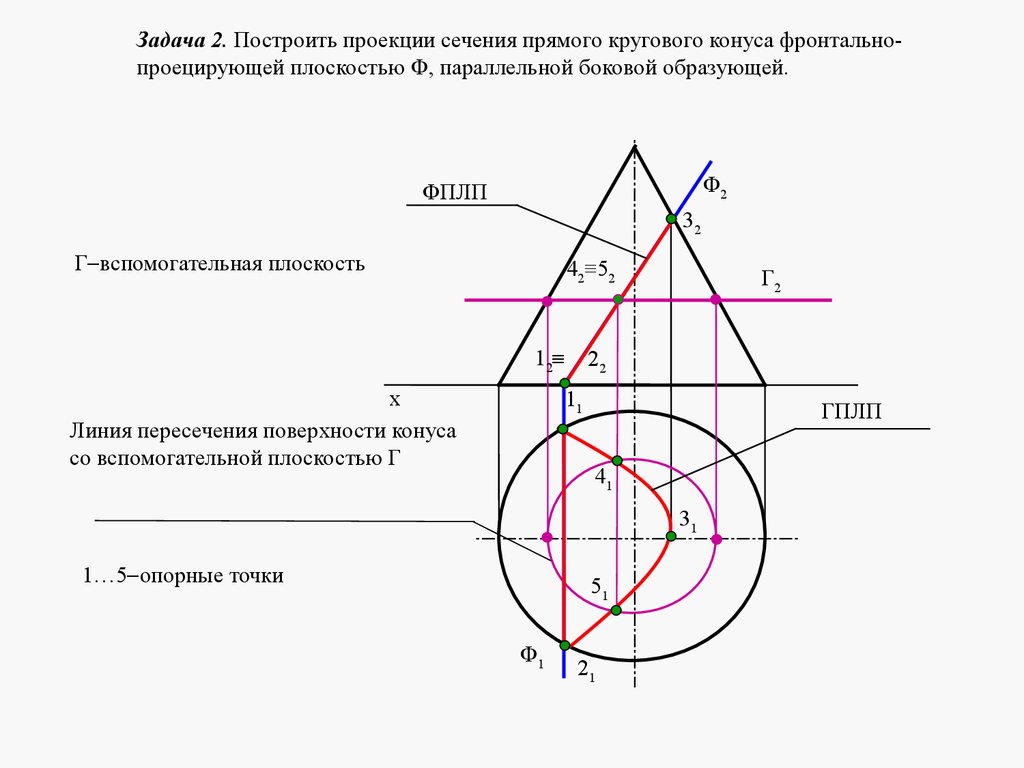
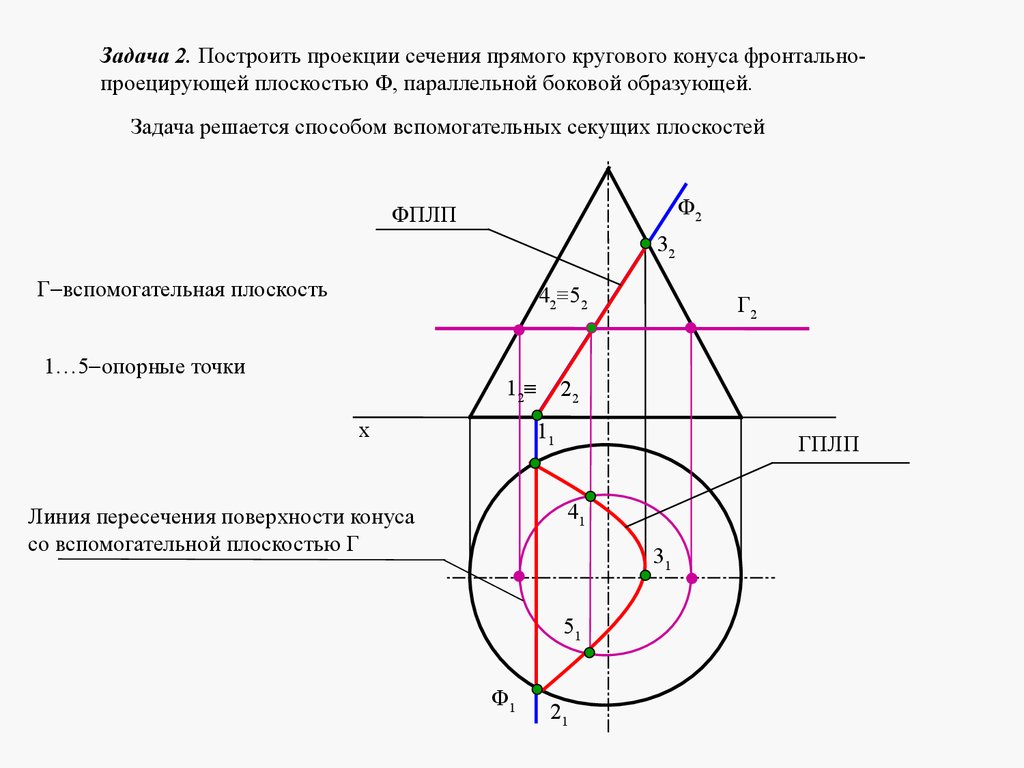

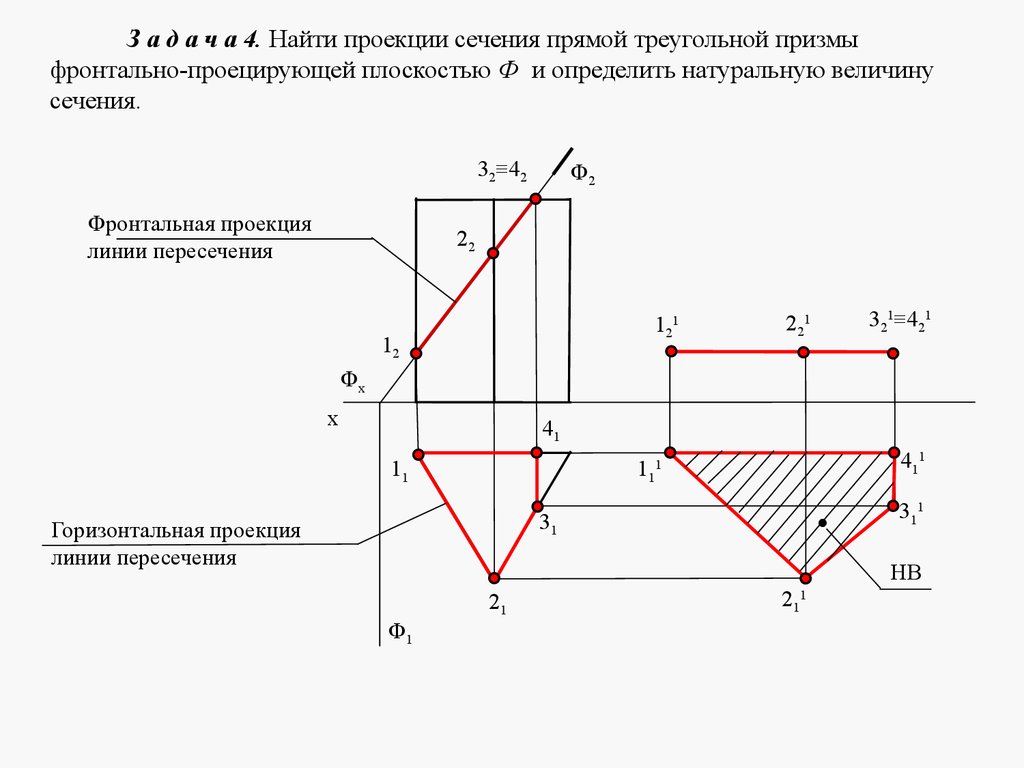
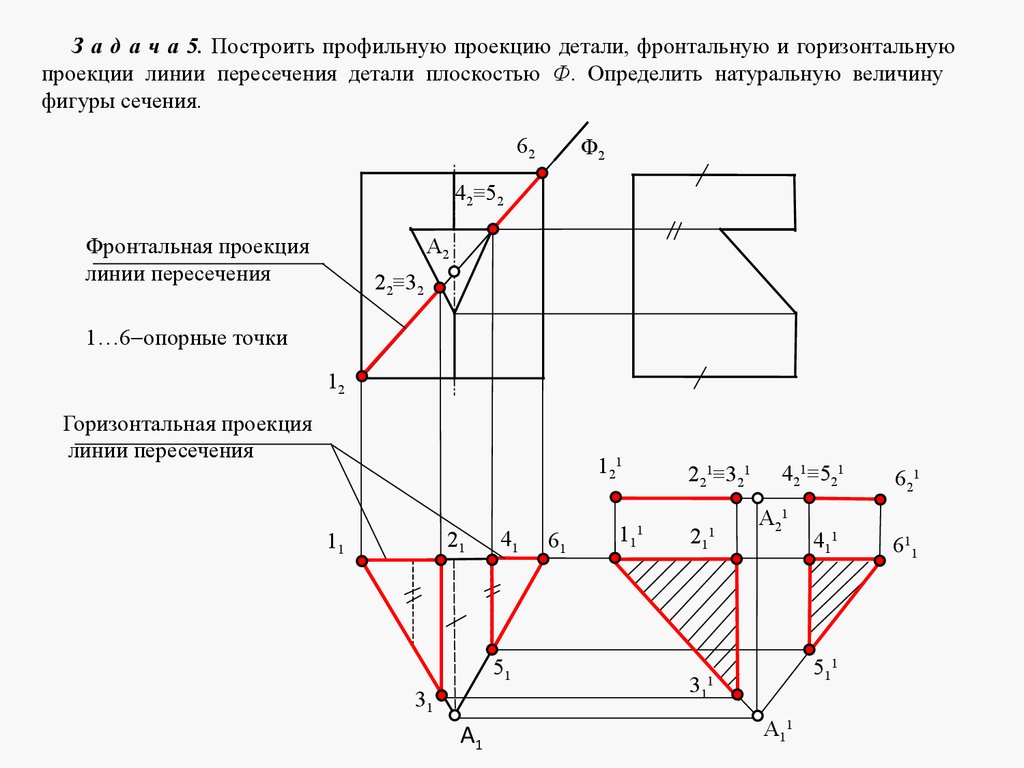
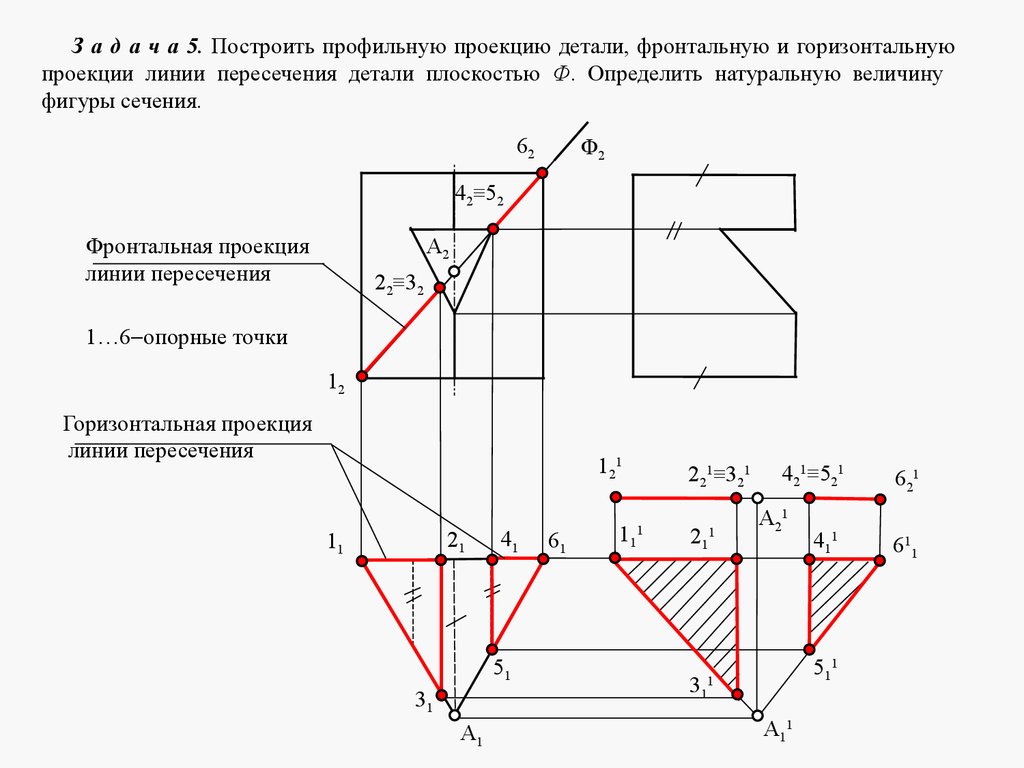
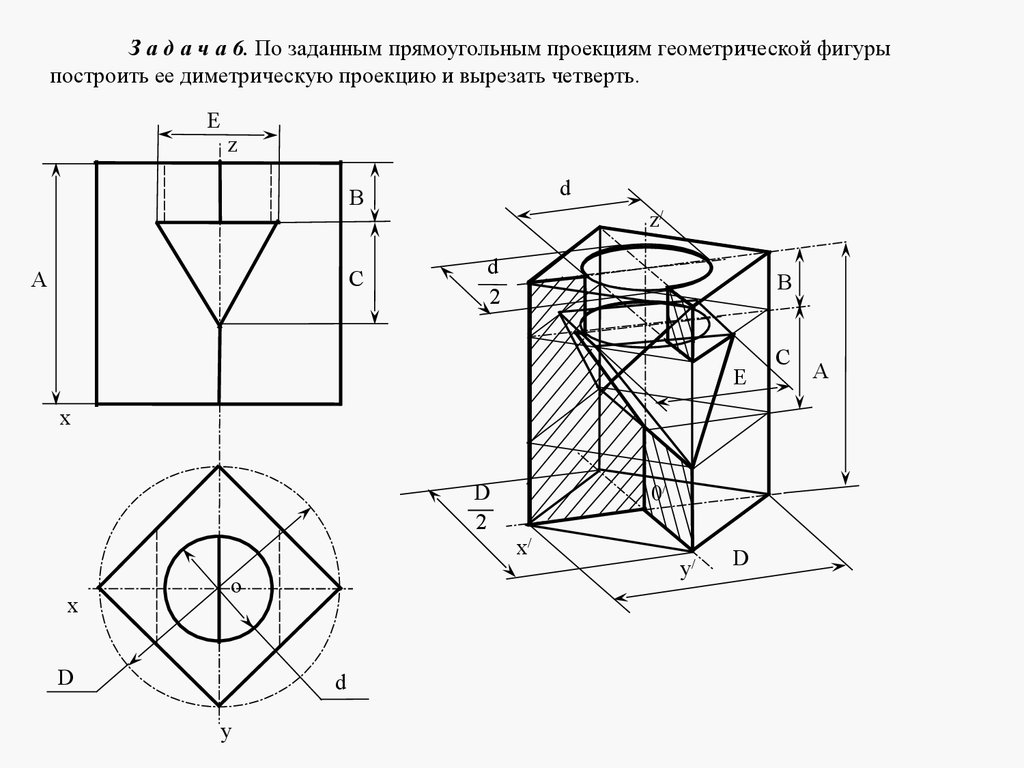
 mathematics
mathematics drafting
drafting








