Similar presentations:
Возникновение алгебры. Кружок, 7 класс
1. Возникновение алгебры
КРУЖОК, 7 КЛАССР А Б О Т У В Ы П О Л Н И Л И С Т УД Е Н Т К И Г Р У П П Ы М И - 1 6 :
МЕДВЕДЕВА Е.
ГА Н И Е В А К .
2. Можно ли представить мир без чисел?
Первоначально для записей чисел использоваликамень или выполняли засечки на дереве.
3.
Около 5 тысяч лет назад у разных народов (вВавилоне, Египте, Китае) появился новый способ
записи чисел с помощью особых знаков – цифр
Глиняная табличка с
клинописью
Папирус
4.
Где можно встретить Римскую нумерацию в нашидни?
5.
Современные цифры 1,2,3,…,0 – ценнейший вклад всокровищницу математических знаний. Очень скоро
эти цифры заимствовали арабы. От них эти цифры
распространились в Х –ХIII вв. в Европе, а затем и во
всем мире. Европейцы назвали их арабскими. Это
название цифр сохранилось до наших дней.
У народов какой страны эти цифры позаимствовали
арабы?
Решим ребус, чтобы это узнать
6.
Ответ: у индусов, Индия7.
В древности положительные и отрицательные числатолковали по-иному. Положительные числа выражали
имущество, а отрицательные - долг.
Правила знаков при умножении положительных и
отрицательных чисел впервые сформулировали
индийские ученые
«Минус на минус – всегда только плюс.
Отчего так бывает, сказать не берусь!»
8. Решив примеры, вы узнаете, кто придумал отрицательные числа
-1,68 + (-1,68) =4,61 + (-2,29) =
- 5,5 – 2,8 =
25 – 32 =
-6,3- (-3,2)=
6,9 ⋅ (- 0,1)=
(- 4/7) ⋅ (-7/8) =
9. Решив примеры, вы узнаете, кто придумал отрицательные числа
-1,68 + (-1,68) = -3,36;4,61 + (-2,29) = 2,32;
- 5,5 – 2,8 = - 8,3;
25 – 32 = -7;
-6,3- (-3,2)= -3,1;
6,9 ⋅ (- 0,1)= - 0,69;
(- 4/7) ⋅ (-7/8) = ½
Д
И
О
Ф
А
Н
Т
10. Как появилось слово алгебра?
В первой половине IX в. появилась книга на арабскомязыке под названием «Китаб аль-джебр ва-льмукабала».
صر
َ َ ا ْل ِكتَاب ا ْل ُم ْخت
ساب ا ْل َجبْر
َ فِي ِح
ََوا ْل ُمقَابَلة
Первая страница книги
11. Разгадав кроссворд, вы узнаете его имя
12.
1. Деление числителя и знаменателя на одно и тоже число, не равное нулю.2. Число, на которое делят делимое
3. Древнегреческий математик, нашедший для числа π значение 22/7
4. Действие, при помощи которого находится дробь от числа.
5. Сотая часть числа.
6. Частное двух чисел.
7. Число в дроби, показывающее, на сколько долей разделили целое.
8. Дробь, у которой числитель и знаменатель взаимно просты числа.
9. Название дроби, у которой числитель больше или равен знаменателю.
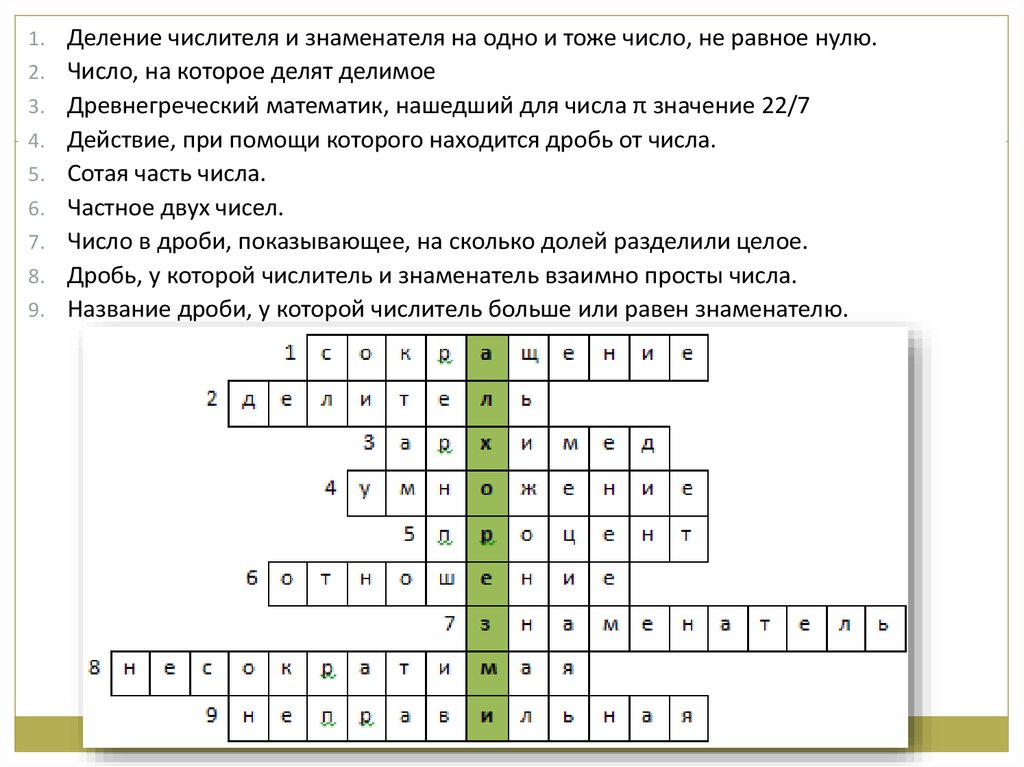
13.
1. Деление числителя и знаменателя на одно и тоже число, не равное нулю.2. Число, на которое делят делимое
3. Древнегреческий математик, нашедший для числа π значение 22/7
4. Действие, при помощи которого находится дробь от числа.
5. Сотая часть числа.
6. Частное двух чисел.
7. Число в дроби, показывающее, на сколько долей разделили целое.
8. Дробь, у которой числитель и знаменатель взаимно просты числа.
9. Название дроби, у которой числитель больше или равен знаменателю.
14. Муха́ммад ибн Муса́ ал-Хорезми́
15.
В истории арифметики и алгебры большое значениеимеют, труды ал-Хорезми(Хорезмийский математик и
астроном). Написанный им в начале IX в. алгебраический
трактат, известный под названием «Китаб аль-джебр валь-мукабала» (Книга о восстановлении и
противопоставлении), явился первым в мире
самостоятельным сочинением по алгебре.
От второго слова в названии этой книги «ал-джебр» ,
произошло наше слово «алгебра». Само слово «ал-джебр»
обозначает «восстановление».
Алгебру ал-Хорезми в латинском переводе изучали
европейцы на протяжении XII-XVI вв. Дальнейшее
развитие алгебры связано с именами европейских ученых
Ф. Виета, Р. Декарта, И. Ньютона, Л. Эйлера и др.















 mathematics
mathematics pedagogy
pedagogy








