Метрология: применение математической статистики при измерениях и испытаниях

1. Лекция 8

1 Метрология: применение
математической статистики
при измерениях и испытаниях.
2 Проверка статистических гипотез.
Ошибки первого и второго рода.
3 Нормальный (гауссовский) закон
распределения случайной величины.
Вычисление вероятности по
нормальному закону распределения.

2. МЕТРОЛОГИЯ

Применение математической
статистики
при измерениях и испытаниях

3. Статистические гипотезы. Проверка гипотез. Односторонний и двухсторонний критерии

Генеральная совокупность
случайной величины (СВ) бесконечное (очень большое)
число наблюдений СВ.
Выборочная совокупность –
выборка ограниченного объема
из генеральной совокупности.

4. Закон распределения генеральной совокупности. Плотность распределения

F ( x ) P( X x )
F ( b) F ( a ) P ( a x b)
- непрерывная
функция
распределения
Х – случайная величина
f ( x ) dF
dx
- плотность непрерывного
распределения
F x f x dx
- связь между функцией
и плотностью распределения

5.

Статистическая гипотеза (СГ) –
некоторое предположение относительно
вида неизвестного или о параметрах
известного распределения генеральной
совокупности СВ.
Проверка СГ заключается
в сопоставлении неких статистических
показателей (Θ - критериев проверки),
вычисляемых по выборке,
со значениями Θкр. , которые определены
при верной проверяемой гипотезе.

6.

ЭТАПЫ ПРОВЕРКИ СГ
1 Выдвигают основную ( Н0 : )
и одновременно альтернативную ( Н1 : )
гипотезы.
2 Вычисляют по выборке СВ некий
статистический критерий ( Θрасч. ) .
3 Сравнивают рассчитанное значение
Θрасч. с критическим Θкр. (табличным).
4 В зависимости от результатов сравнения
Θ>Θрасч.(Θ<Θрасч.) принимают Н0 : или Н1 :

7.

Θрасч. - это специально подобранная
CВ, точное или приблизительное
распределение которой известно.
Проверка СГ заключается
в сопоставлении Θрасч.
со значением Θкр. , которое
определено в предположении,
что проверяемая гипотеза верна.

8. Условия принятия (отбрасывания) гипотез:

1 Н0 : - принимается, если Θрасч.
не попадает в критическую
область, при этом отвергается Н1 :
2 Н1 : - принимается, если Θрасч.
попадает в критическую область,
одновременно отвергается Н0 :

9. Односторонний критерий принятия гипотезы

Для одностороннего (правостороннего)
критерия вероятность попасть Θрасч.
в критическую область (заштрихована)
равна Р (Θрасч.> Θкр.) = q
q - есть уровень значимости

10.

Для левостороннего критерия
вероятность попадания Θрасч.
в критическую область равна
Р (Θрасч.< Θкр.) = q
Вероятность попадания Θрасч.
в область принятия гипотезы Н0
равна α = 1- q
α - есть доверительная вероятность

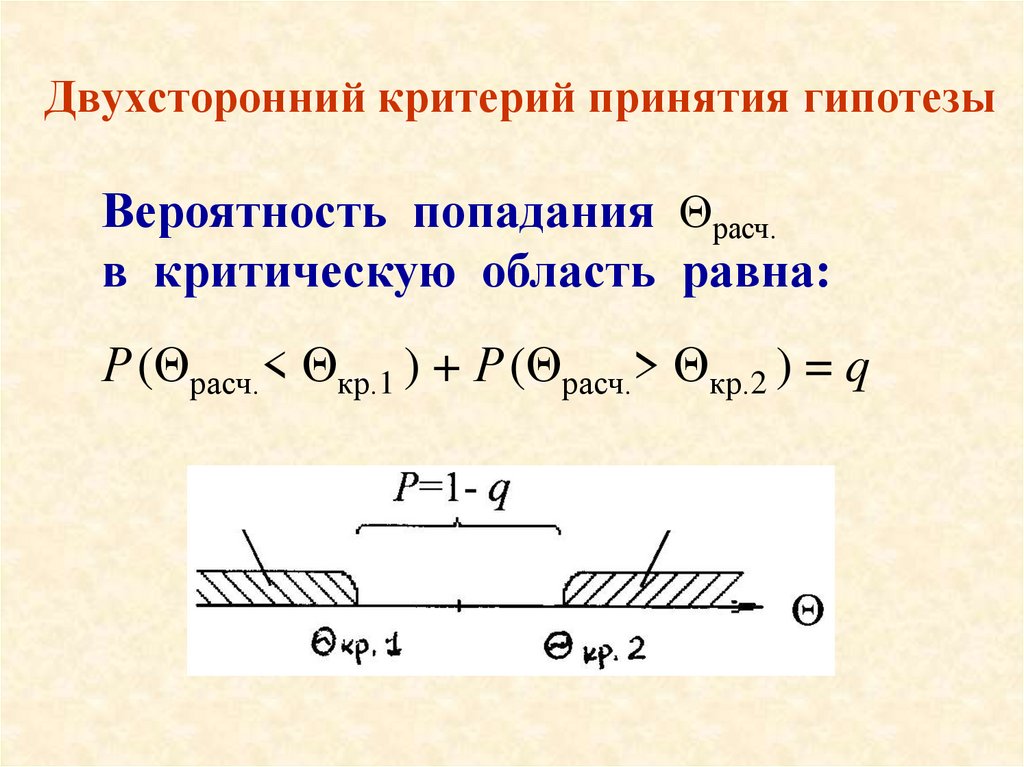
11. Двухсторонний критерий принятия гипотезы

Вероятность попадания Θрасч.
в критическую область равна:
Р (Θрасч.< Θкр.1 ) + Р (Θрасч.> Θкр.2 ) = q

12.

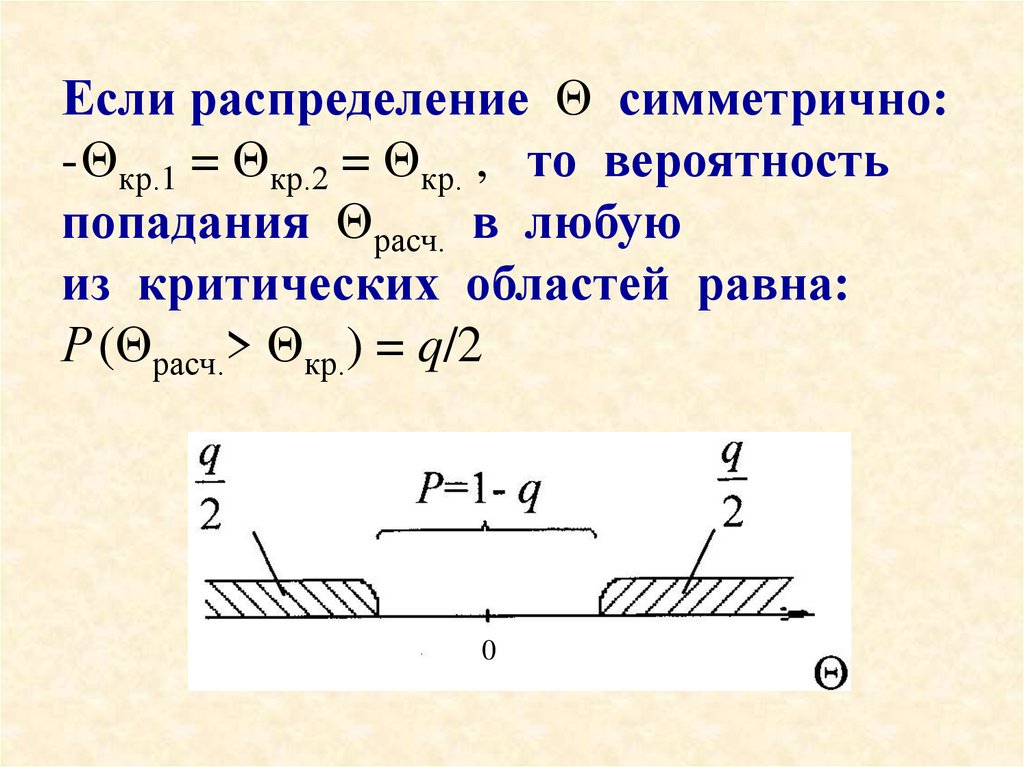
Если распределение Θ симметрично:
-Θкр.1 = Θкр.2 = Θкр. , то вероятность
попадания Θрасч. в любую
из критических областей равна:
Р (Θрасч.> Θкр.) = q/2
0

13.

Практическое правило:
Для двухстороннего критерия
численное значение q*/2 = 0,05
берут таким же, как для
одностороннего критерия q = 0,05
В этом случае вероятность ошибки
второго рода будет одинаковой для
одностороннего и двухстороннего
критерия (для последнего критерия
получаем q*= 0,10 )

14. Как найти границы критической области ?

Рассмотрим правостороннюю область.
Для нахождения Θкр. задаются малой
вероятностью q (0,05; 0,025; 0,01) .
Затем ищут Θкр. ,
исходя из неравенства Р (Θ > Θкр.) = q

15.

Это означает, что вероятность
события Θ > Θкр. мала,
и в единичном испытании оно
не должно наступить. Если все же
событие произошло, то Н0 : ложна.

16. Ошибки первого и второго рода:

Ошибка 1-го рода – отвергнуть
верную гипотезу (Н0 :) .
Причем Н0 : действительно верна.
Её вероятность составляет не более q.
При q = 0,05 ошибка 1-го рода
произойдет в 5 случаях из 100.
Ошибку 1-го рода называют
риском производителя

17.

Ошибка 2-го рода – принять
ложную гипотезу (Н0 :) за верную.
Причем Н0 : действительно
ложная. Оценить вероятность её
очень сложно. При увеличении q ,
увеличивается число отвергаемых
гипотез! Ошибку 2-го рода
называют риском потребителя

18.

Если вероятность ошибки 2-го
рода принять равным β, то (1- β)
называют мощностью критерия это вероятность отклонения Н0 : ,
когда она ложная. Мощность
критерия характеризует
вероятность ошибочного
применения ложной гипотезы Н0 .
1-β – вероятность не совершить
ошибку второго рода.

19.

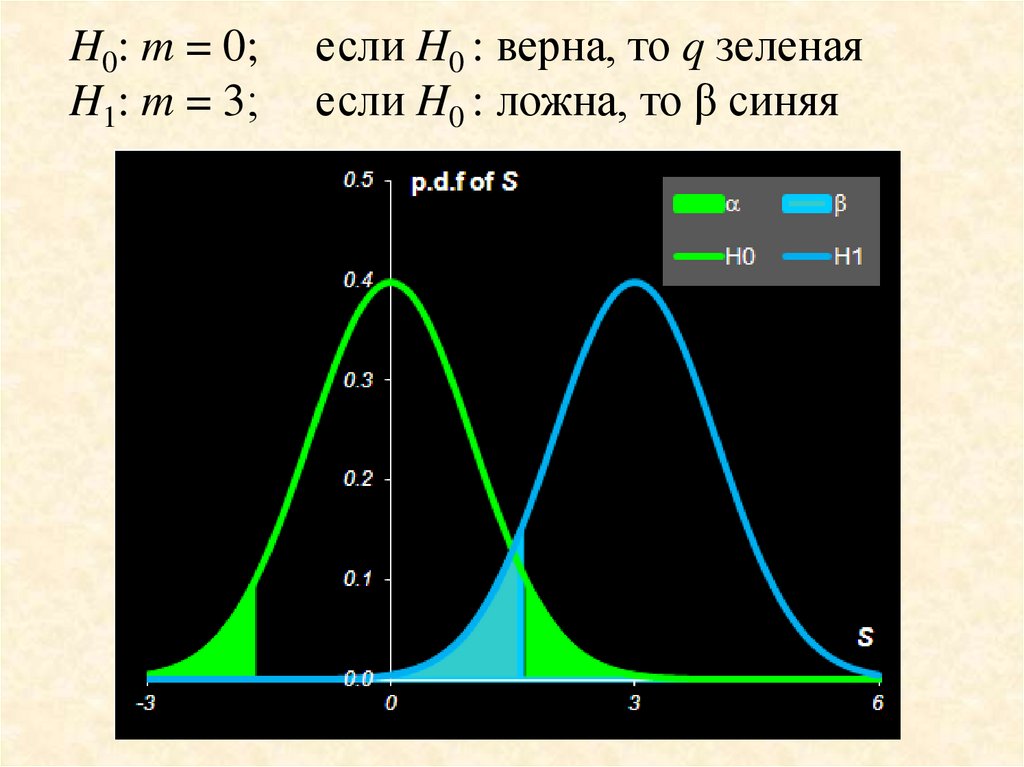
H0: m = 0;
H1: m = 3;
если H0 : верна, то q зеленая
если H0 : ложна, то β синяя

20.

Мощность критерия должна быть
максимальной, это обеспечивает
минимальность ошибки 2-го рода.
Если уменьшать q , то β будет
возрастать при n = const .
Единственный способ
одновременного уменьшения
q и β - это увеличение объема
выборки (n) !

21.

Нормальный (гауссовский) закон
распределения случайной величины
Карл Фридрих Гаусс
30.04.1777 - 23.02.1855
великий немецкий
математик, астроном и
физик. Считается одним
из величайших
математиков всех
времён
«Король математиков»

22. СВ распределена по нормальному закону, если плотность её распределения описывается выражением:

1
f ( x)
e
2
( x x )2
2 2
x – генеральное мат. ожидание СВ
σ 2 – генеральная дисперсия СВ

23.

f(x)
1=1
2=2
3=4
x
0
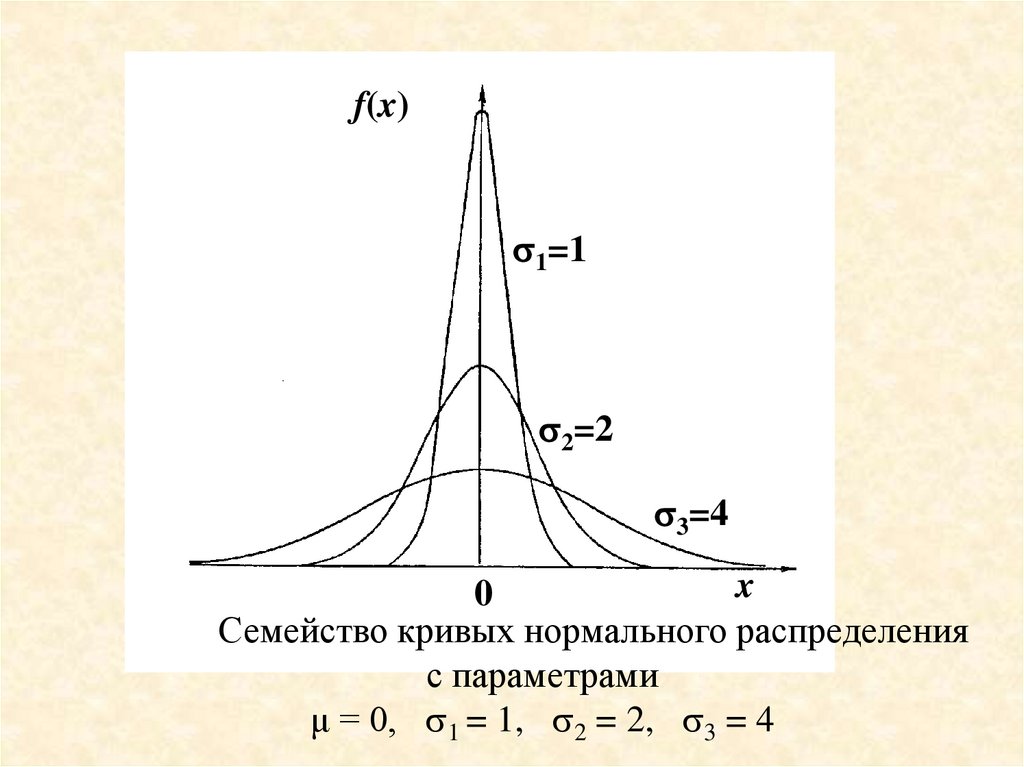
Семейство кривых нормального распределения
с параметрами
μ = 0, 1 = 1, 2 = 2, 3 = 4

24. Характеристики кривой НР:

1 Симметрия относительно центра
распределения: F ( x) 1/ 2
Медиана равна мат. ожиданию x x
2 Мода – в центре
распределения
3
1
f ( x)
2
f(x)>0
4 Точки перегиба – при x x

25. Вычисление вероятности по нормальному закону распределения

Пусть случайная величина Х
распределена по нормальному закону,
тогда вероятность найти Х < х равна:
P X x F ( x)
x
f ( x)dx
1
2
x
e
x x 2
2 2
dx

26. Перейдем к интегралу вероятности

F x 1/ 2 → из свойства F(x)
1
1
F x
2
2
x 0; 1; x t
1
F ( x)
2
x
e
( x x )2
2 2
dx
x
- центрирование, нормировка,
замена переменной
x
1
e
2 0
t2
2
dt

27.

x
1
( x)
e
2 0
t2
2
dt
- функция
Лапласа
Свойства функции Лапласа:
(0) 0;
( ) 0,5;
( ) 0,5
нечетная
( t ) (t )
функция
F ( x) 1 ( x )
2

28.

Пьер-Симо́н, маркиз де
Лапла́с (Pierre-Simon de Laplace)
23.03.1749-05.03.1827.
Французский
математик, механик, физик
и астроном. Известен работами
в области небесной механики,
диф.уравнений, один из
создателей теории вероятности.
Заслуги Лапласа в области
теоретической
и прикладной математики
и, особенно в астрономии,
громадны: он усовершенствовал
почти все отделы этих наук.
Был членом Французского
географического общества.

29.

x
Таблица значений функции
х
Ф(х)
1
( x)
e
2 0
х
t2
2
Ф(х)
0.00
0.0000
1.00
0.3413
0.10
0.0398
2.00
0.4772
0.30
0.1179
3.00
0.49865
0.50
0.1915
5.00
0.499997
dt

30.

Вычисление вероятности
нахождения СВ, распределенной
по НЗ, в интервале от a до b
по функции (интегралу) Лапласа

31.

Заменим СВ х
по НЗ на x
x x
1
получим F ( x)
2
x x
Если генеральные МО и дисперсия
известны, то вероятность найти “х”
в интервале (a, b) :
P ( a x b) F ( b) F ( a )
b x
a x

32.

Перейдем от “ x ” к отклонению
от мат.ожидания U x x ,
и переформулируем задачу:
B
A
P A U B ,
где : A a x ;
B b x .

33.

Если интервал (А, В) симметричен:
A= – B и В > 0 , т.к. Ф(х) - нечетная:
B
A
Тогда вероятность найти:
B
P U B 2
(1)

34.

Пример 1: вычислим по (1) какова
вероятность, что U , т.к. В ≡ σ ,
то
B
1 есть аргумент
P U 2 1
1 0,3413
P U 0,6826 2
3
При n→∞ в 2/3 наблюдений U x x
не превышает σ !!!

35.

Пример 2: вычислим какова
вероятность, что U 2 , т.е.
P U 2 2 2 0,95
B
2
Пример 3: вычислим вероятность,
что U 3 , т.е.
B
3
P U 3 2 3 0,9973
Это правило 1, 2 и 3 σ !!!

36.

x
Таблица значений функции
х
Ф(х)
1
( x)
e
2 0
х
t2
2
Ф(х)
0.00
0.0000
1.00
0.3413
0.10
0.0398
2.00
0.4772
0.30
0.1179
3.00
0.49865
0.50
0.1915
5.00
0.499997
dt