Теория графов

1. Введение в теорию графов

2. Задача прокладки коммуникаций

2
1
5
3
4

3. Граф G:

G=(V,R),
V2
R12
где V – множество
вершин
R – множество рёбер,
соединяющих
пары
вершин
R23
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

4. Граф G:

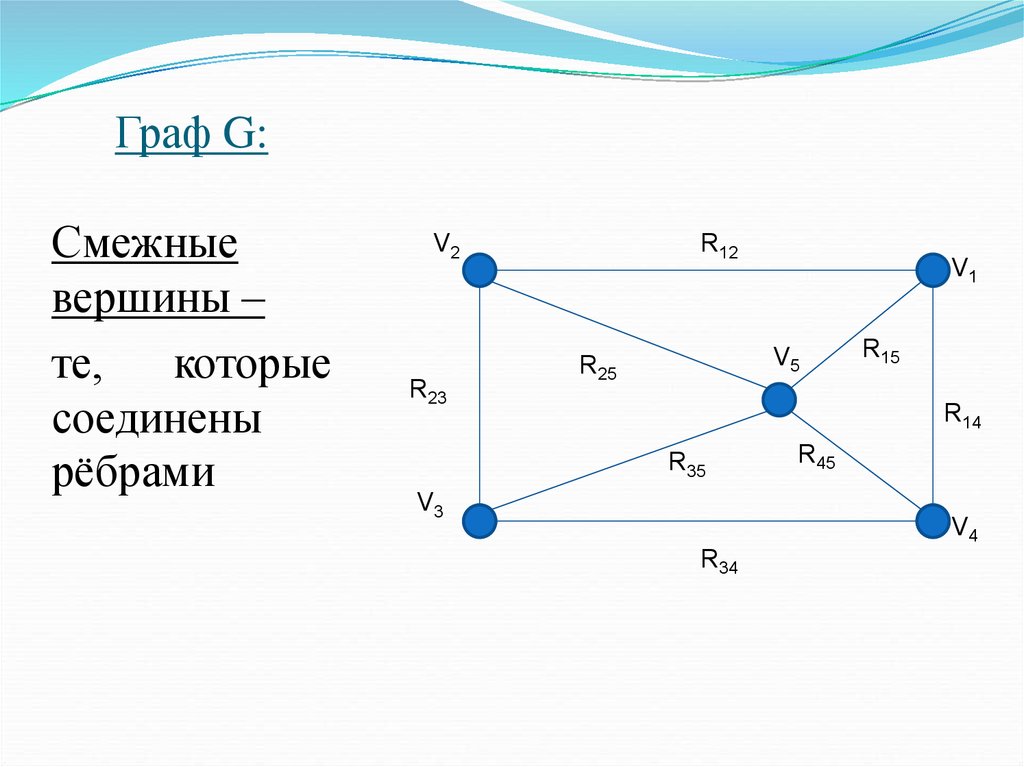
Смежные
вершины –
те,
которые
соединены
рёбрами
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

5. Граф G:

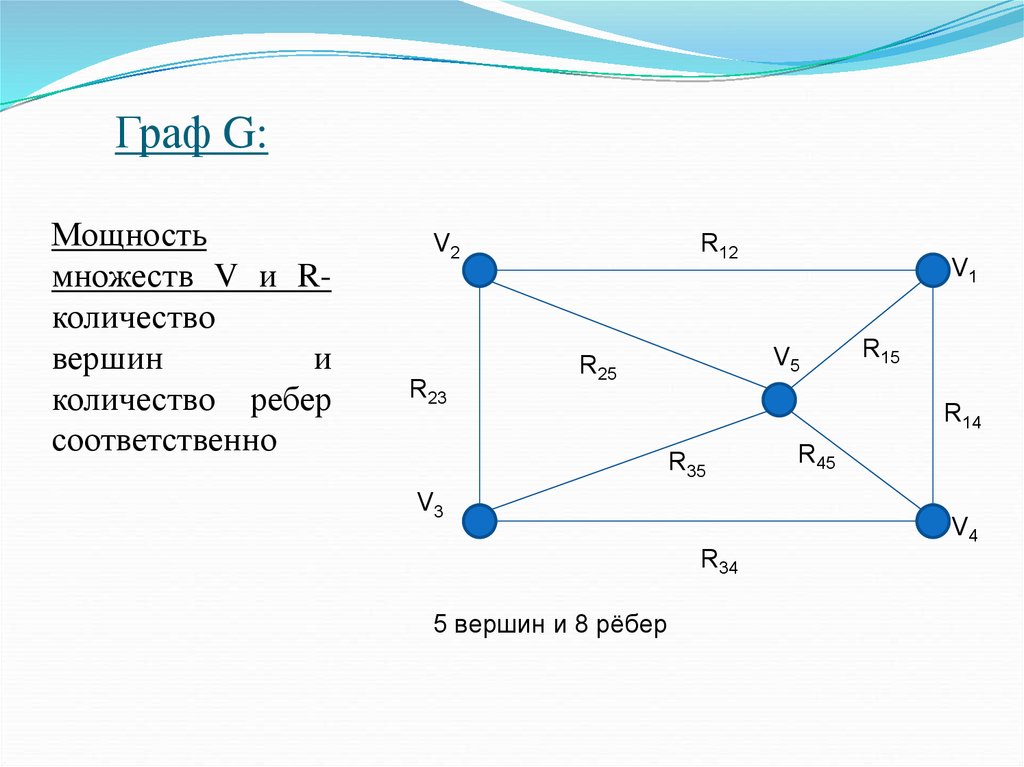
Мощность
множеств V и Rколичество
вершин
и
количество ребер
соответственно
V2
R23
R12
V5
R25
R15
R14
R35
V3
R45
V4
R34
5 вершин и 8 рёбер
V1

6. Граф G:

ребро и любая из
его двух вершин
называются
инцидентными
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

7. Граф G:

Степень вершины
–
количество
инцидентных ей
рёбер
V2
R23
R12
V5
R25
R15
R14
R35
V3
R45
V4
R34
Степень V3 – 3
Степень V5 – 4
V1

8. Граф G:

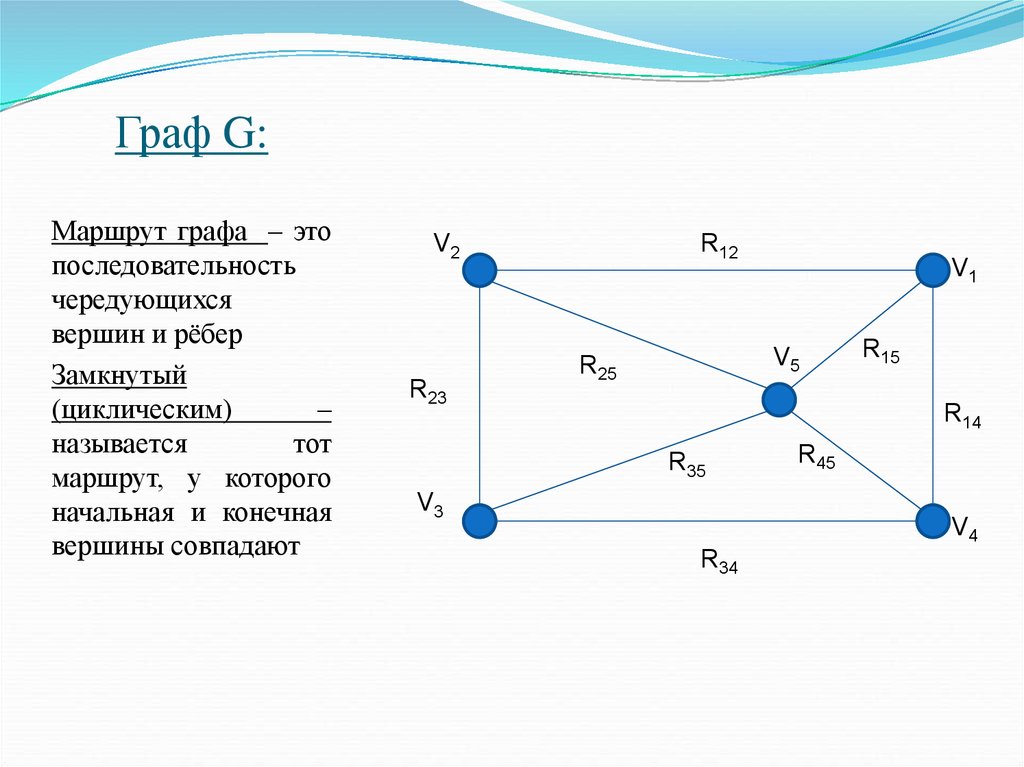
Маршрут графа – это
последовательность
чередующихся
вершин и рёбер
Замкнутый
(циклическим)
–
называется
тот
маршрут, у которого
начальная и конечная
вершины совпадают
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

9. Граф G:

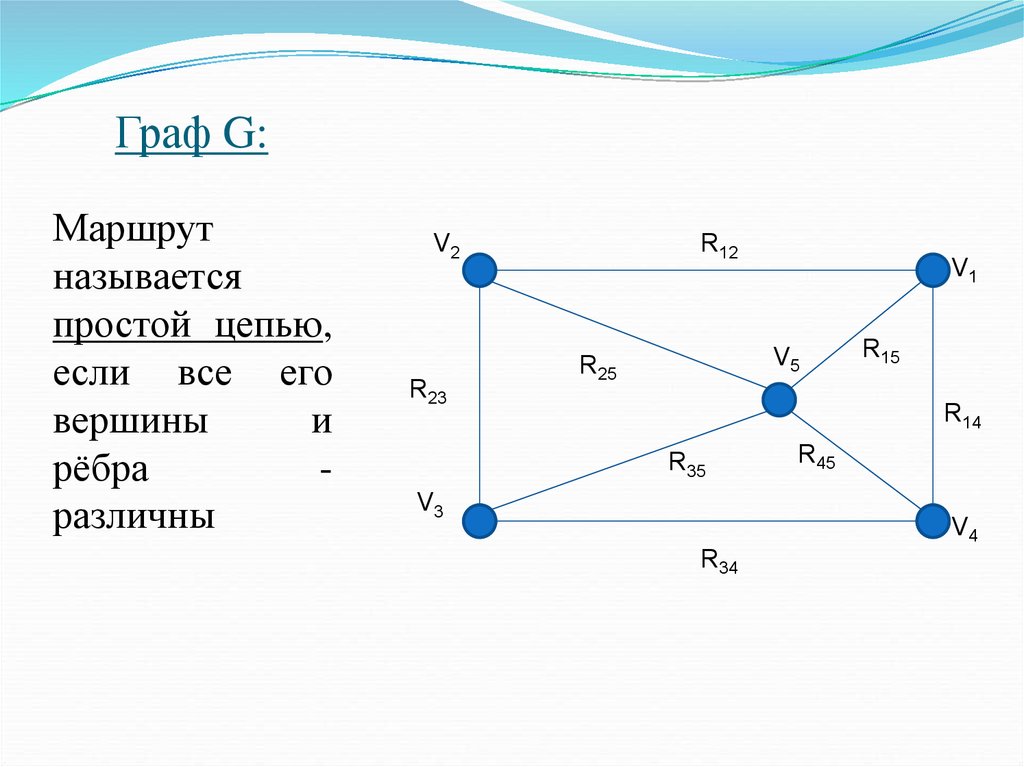
Маршрут
называется
простой цепью,
если все его
вершины
и
рёбра
различны
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

10. Граф G:

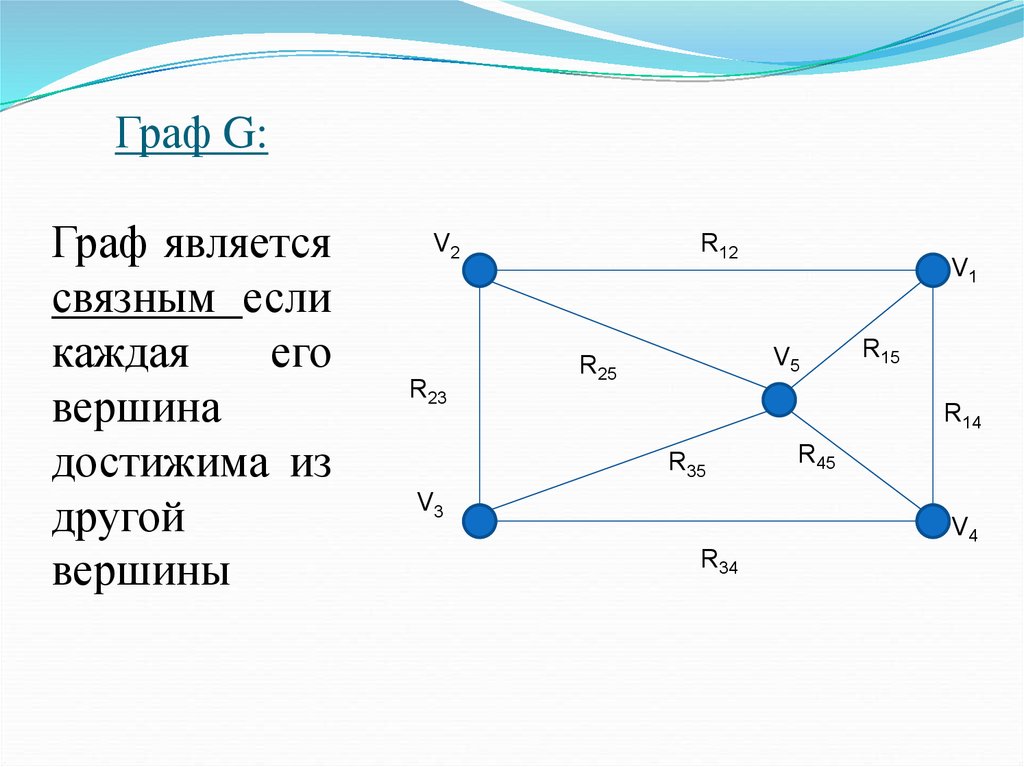
Граф является
связным если
каждая
его
вершина
достижима из
другой
вершины
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

11. Граф G:

Вершины,
не
имеющие
инцидентных
рёбер, называются
изолированными
вершинами.
V6
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34