Введение в теорию графов

1. Введение в теорию графов

2. Задача прокладки коммуникаций

2
1
5
3
4

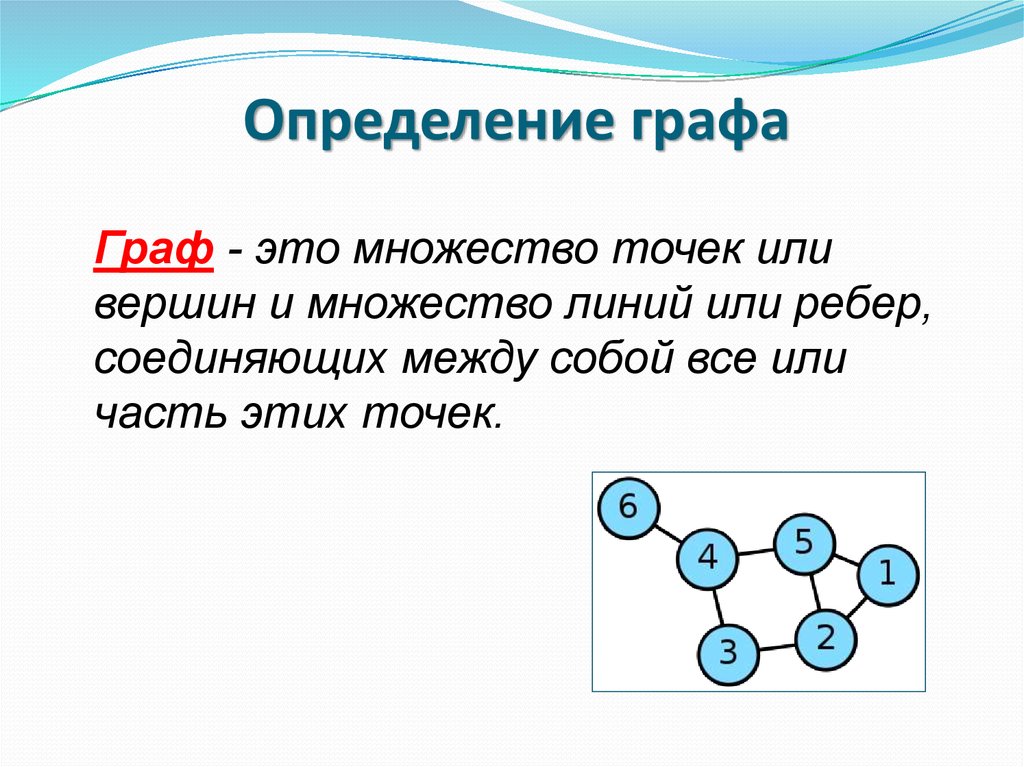
3. Определение графа

Граф - это множество точек или
вершин и множество линий или ребер,
соединяющих между собой все или
часть этих точек.

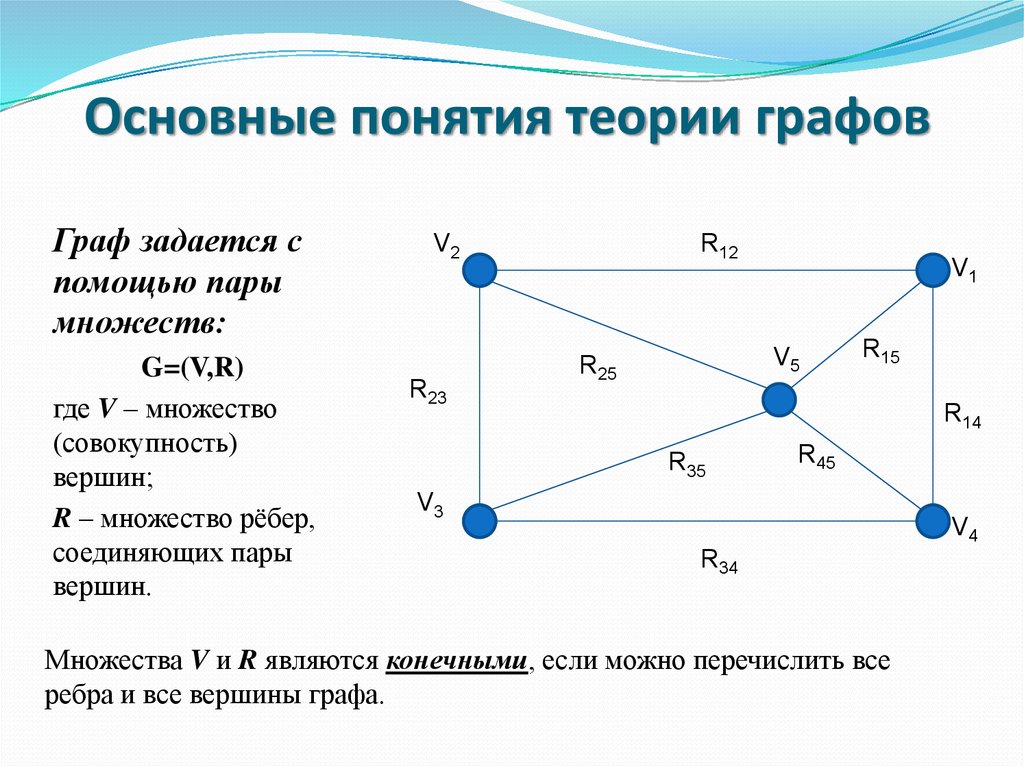
4. Основные понятия теории графов

Граф задается с
помощью пары
множеств:
G=(V,R)
где V – множество
(совокупность)
вершин;
R – множество рёбер,
соединяющих пары
вершин.
V2
R23
R12
V1
V5
R25
R15
R14
R35
R45
V3
V4
R34
Множества V и R являются конечными, если можно перечислить все
ребра и все вершины графа.

5. Граф G:

Смежные
вершины –
это вершины,
которые
соединены
рёбрами.
Граф G:
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

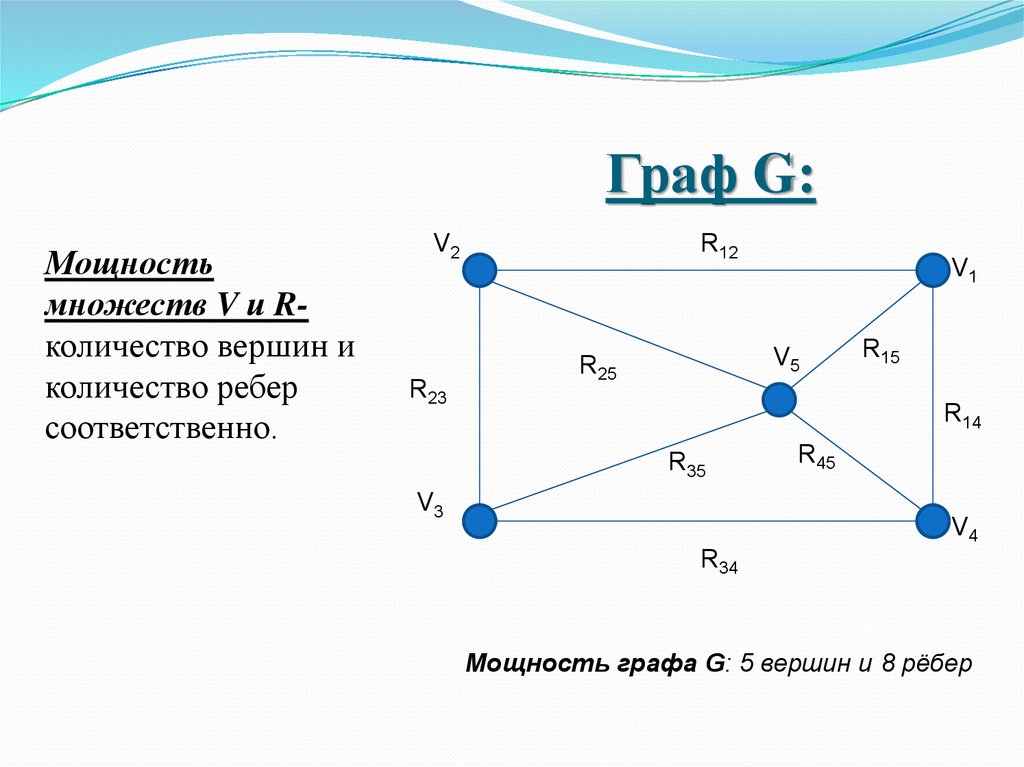
6. Граф G:

Мощность
множеств V и Rколичество вершин и
количество ребер
соответственно.
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34
Мощность графа G: 5 вершин и 8 рёбер

7. Граф G:

Ребро и любая из
его двух вершин
называются
инцидентными
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

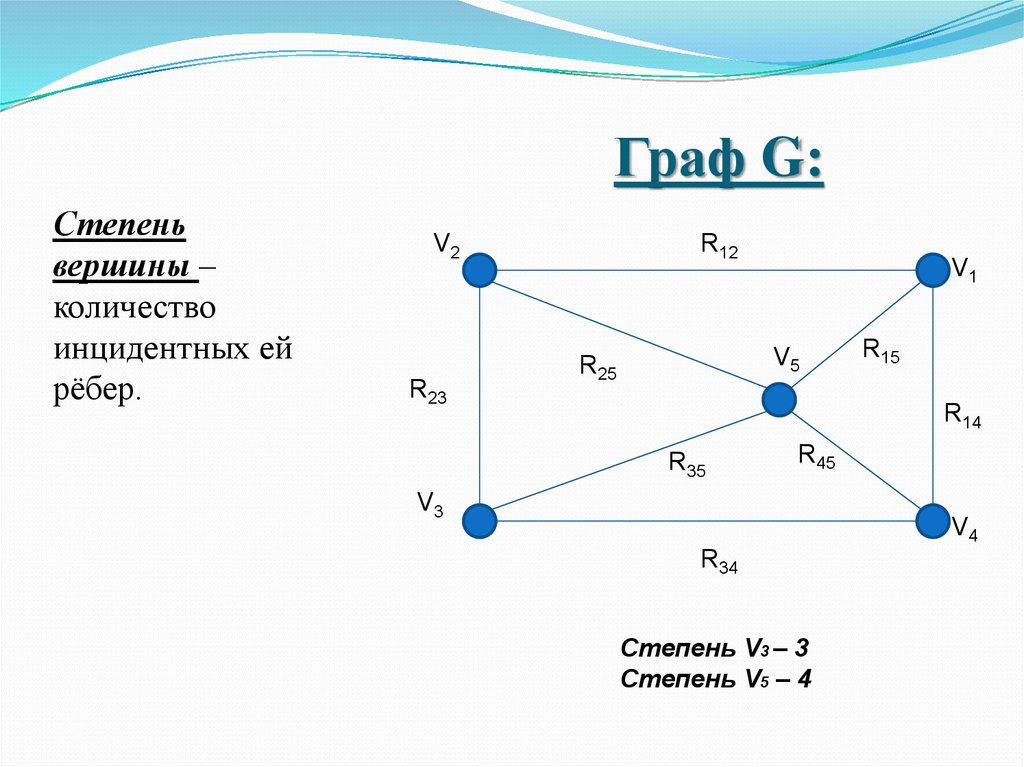
8. Граф G:

Степень
вершины –
количество
инцидентных ей
рёбер.
V2
R23
R12
V1
V5
R25
R15
R14
R35
R45
V3
V4
R34
Степень V3 – 3
Степень V5 – 4

9. Граф G:

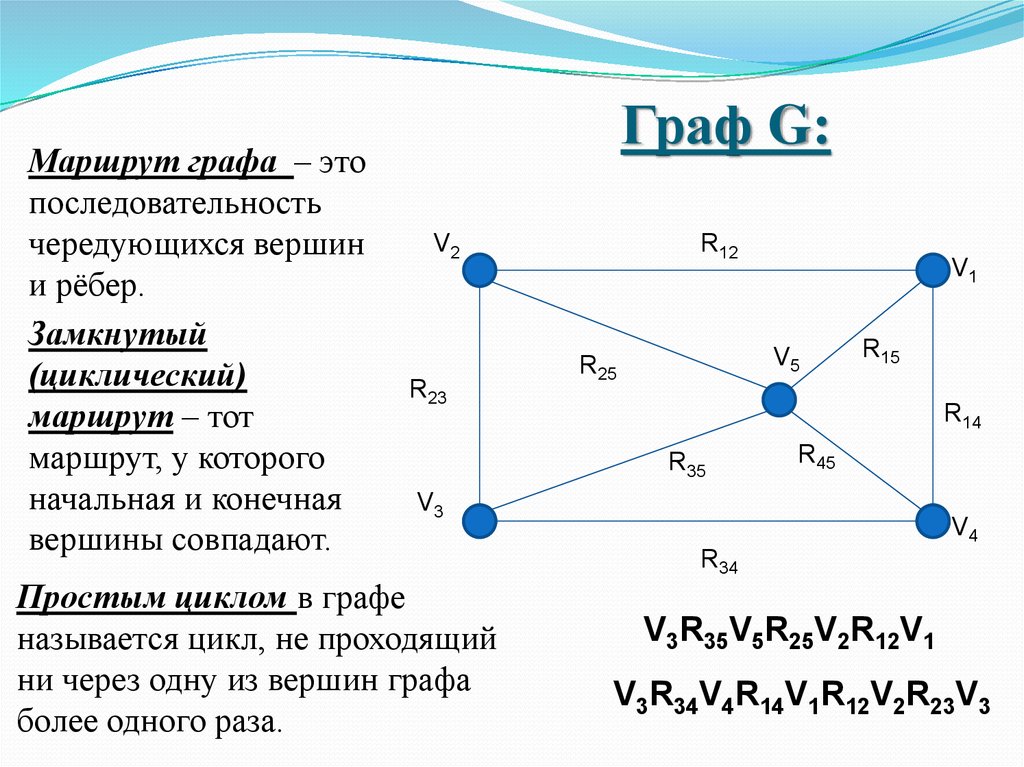
Маршрут графа – это
последовательность
чередующихся вершин
и рёбер.
Замкнутый
(циклический)
маршрут – тот
маршрут, у которого
начальная и конечная
вершины совпадают.
Граф G:
V2
R23
R12
V1
V5
R25
R15
R14
R35
R45
V3
Простым циклом в графе
называется цикл, не проходящий
ни через одну из вершин графа
более одного раза.
V4
R34
V3R35V5R25V2R12V1
V3R34V4R14V1R12V2R23V3

10. Задание 1.

1.
2.
3.
4.
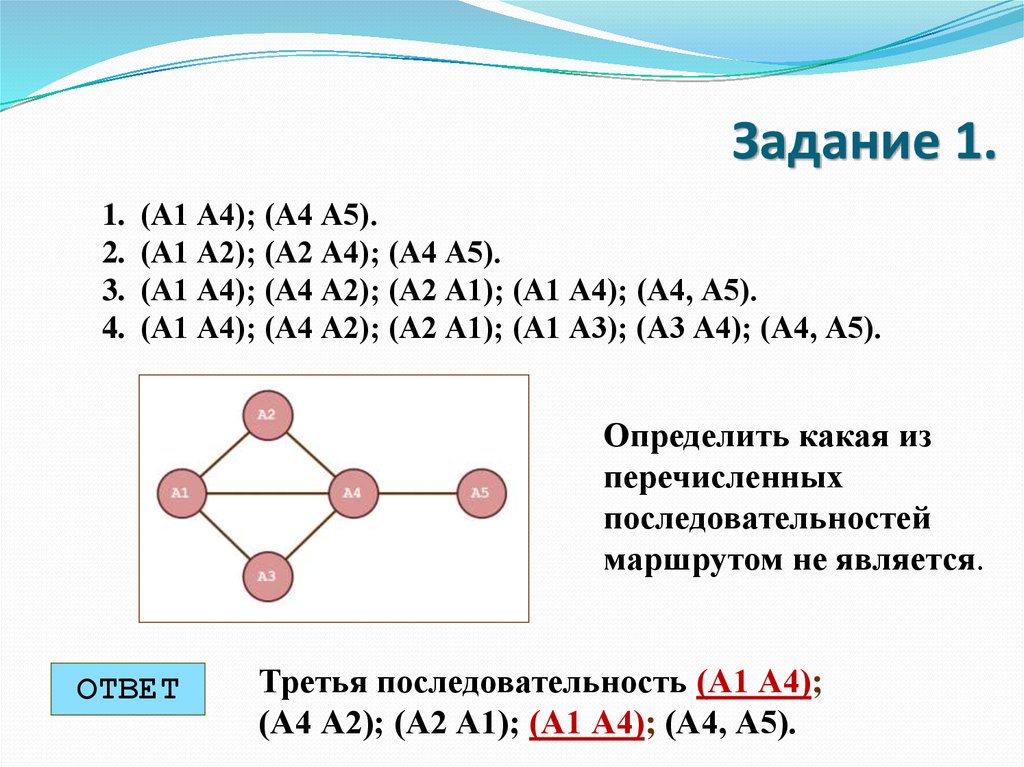
(А1 А4); (А4 А5).
(А1 А2); (А2 А4); (А4 А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А3); (А3 А4); (А4, А5).
Определить какая из
перечисленных
последовательностей
маршрутом не является.
ОТВЕТ
Третья последовательность (А1 А4);
(А4 А2); (А2 А1); (А1 А4); (А4, А5).

11. a) 4 ребра; b) 6 ребер; c) 5 ребер; d) 10 ребер. Какие из этих циклов являются простыми?

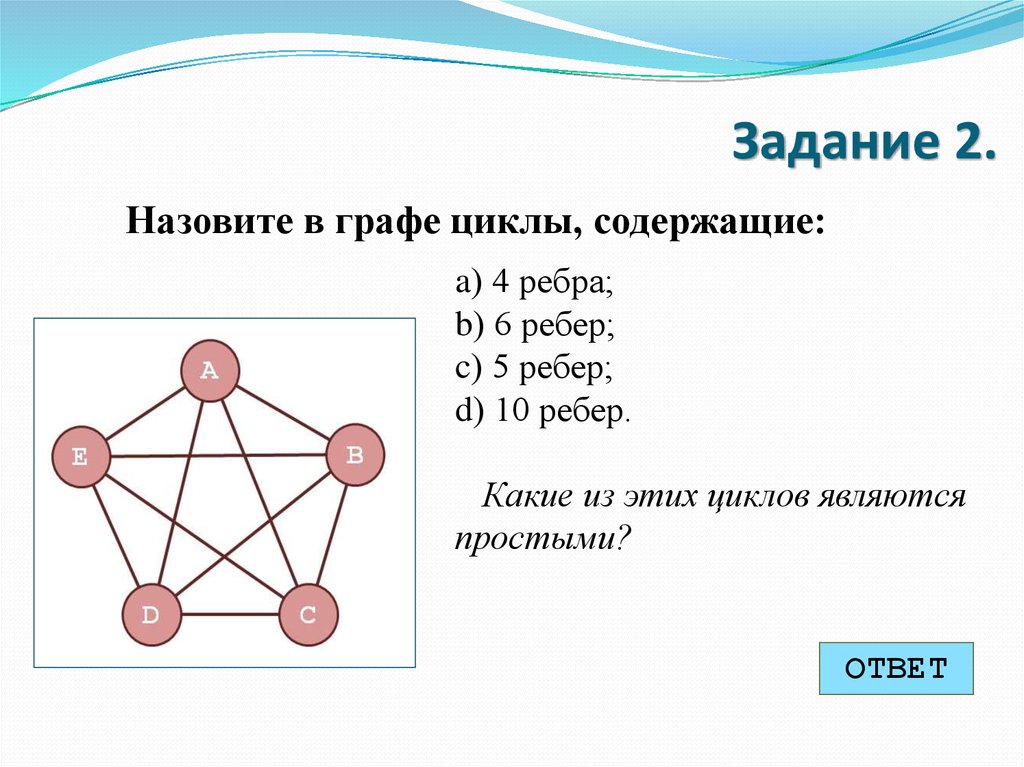
Задание 2.
Назовите в графе циклы, содержащие:
a) 4 ребра;
b) 6 ребер;
c) 5 ребер;
d) 10 ребер.
Какие из этих циклов являются
простыми?
ОТВЕТ

12. ОТВЕТ

Решение:
a) (AB, BC, CE, EA), (CD, DA, AB, BC), (EB, BC,
CD, DE) и т.д. – простые циклы.
b) (DB, BE, EA, AB, BC, CD), (EC, CA, AB, BC, CD,
DE) и т.д. – циклы.
c) (AB, BC, CD, DE, EA), (AC, CE, EB, BD, DA) и
т.д. – простые циклы.
d) (AC, CE, EB, BD, DA, AB, BC, CD, DE, EA), (EB,
BD, DA, AC, CE, EA, AB, BC, CD, DE) и т.д. –
циклы.

13. Граф G:

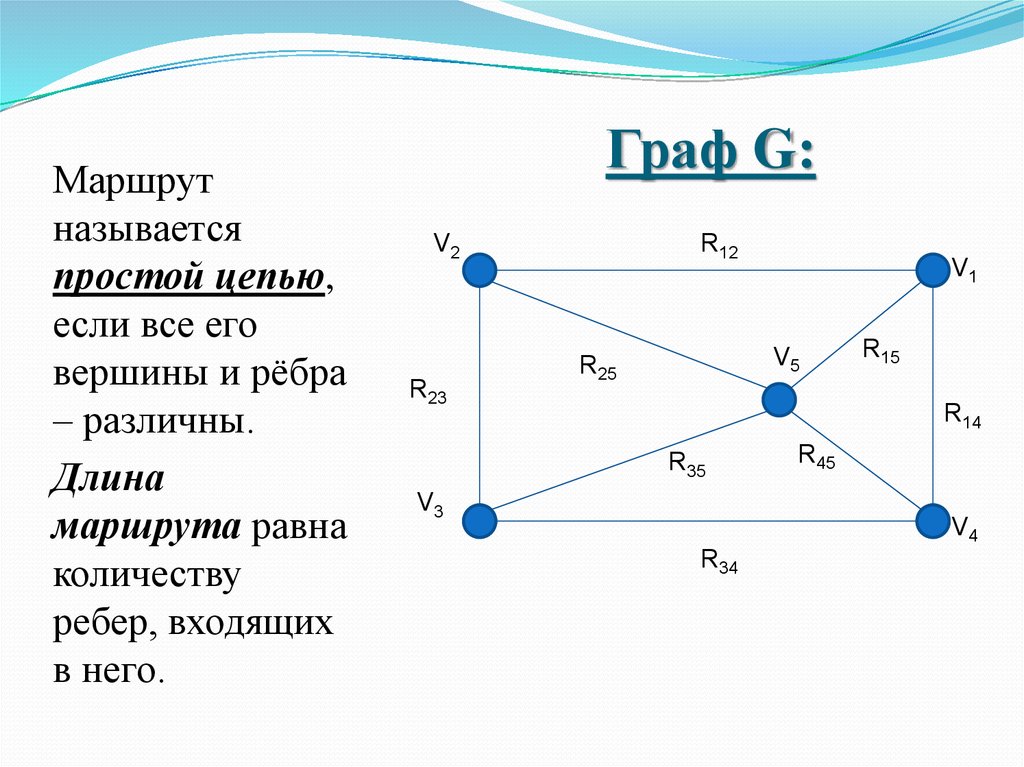
Маршрут
называется
простой цепью,
если все его
вершины и рёбра
– различны.
Длина
маршрута равна
количеству
ребер, входящих
в него.
Граф G:
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

14.

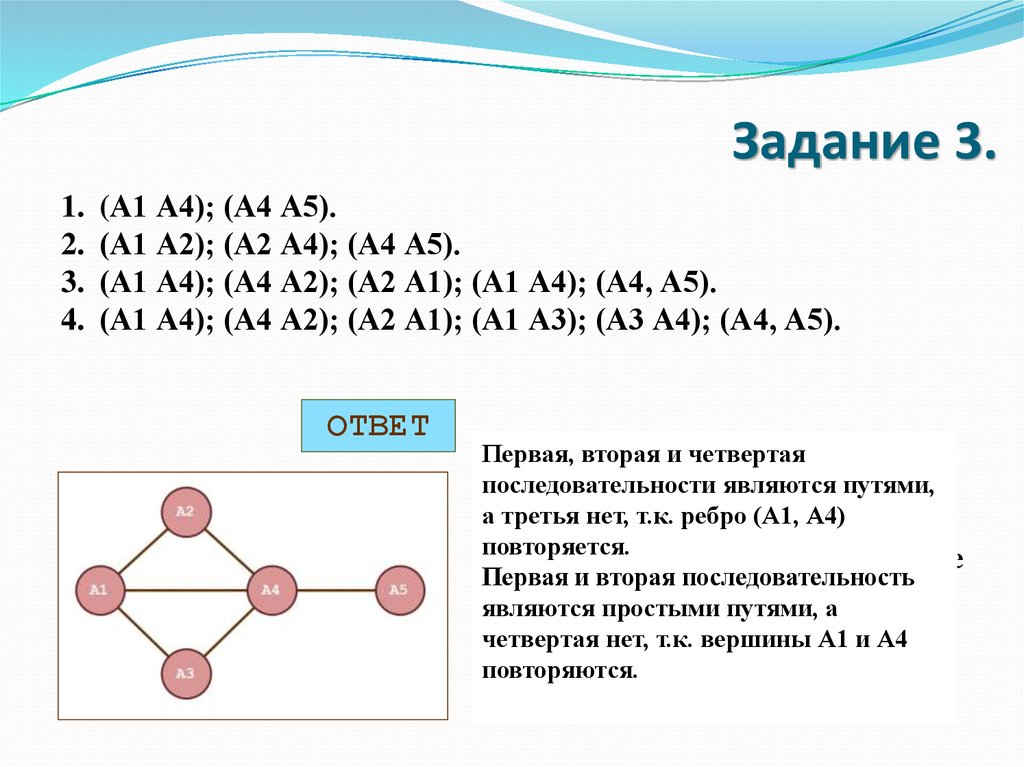
Задание 3.
1.
2.
3.
4.
(А1 А4); (А4 А5).
(А1 А2); (А2 А4); (А4 А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А3); (А3 А4); (А4, А5).
ОТВЕТ
Первая, вторая
и четвертая
Определите,
какие
последовательности являются
путями,
последовательности
ребер являются
а третья нет, т.к.
ребро (А1,
А4)
маршрутами,
и какие
из них
повторяется.
простые.
Если последовательность не
Первая и вторая последовательность
является маршрутом, укажите
являются простыми путями, а
почему.
четвертая нет, т.к. вершины А1 и А4
повторяются.

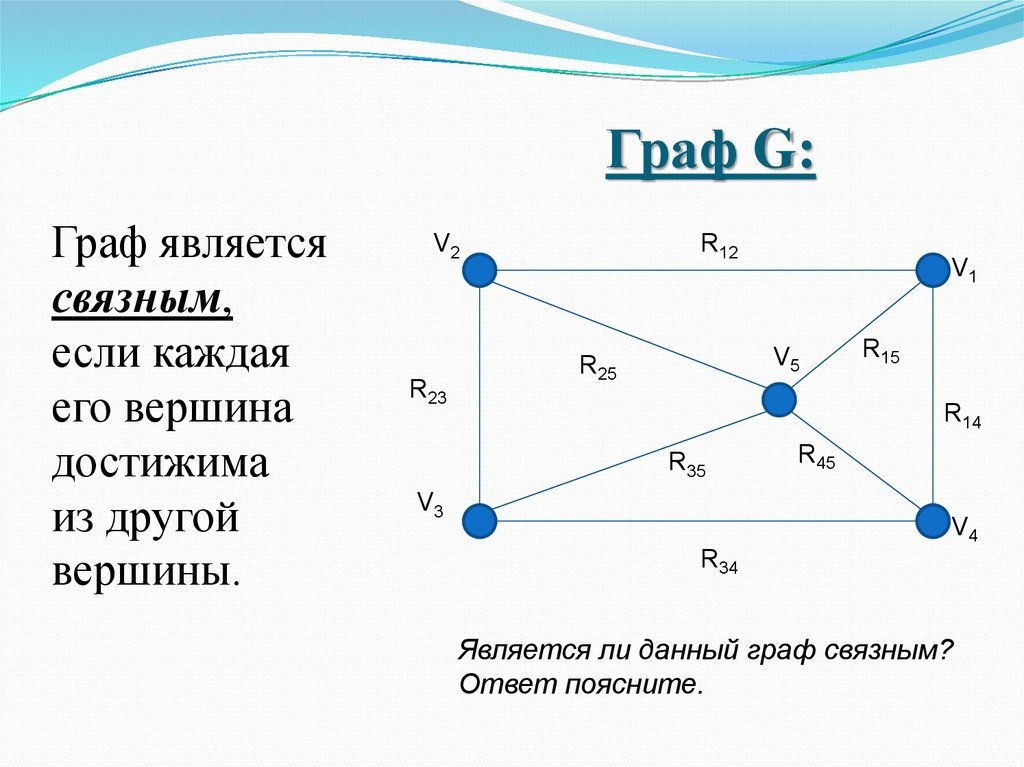
15. Граф G:

Граф является
связным,
если каждая
его вершина
достижима
из другой
вершины.
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34
Является ли данный граф связным?
Ответ поясните.

16. Граф G:

V6
Вершины, не
имеющие
инцидентных
рёбер,
называются
изолированными
вершинами.
Степень таких
вершин нулевая.
V2
R23
R12
V1
V5
R25
R15
R14
R35
V3
R45
V4
R34

17.

Граф, состоящий из «изолированных» вершин,
называется нулевым графом
Рис. 1. Нулевой граф

18.

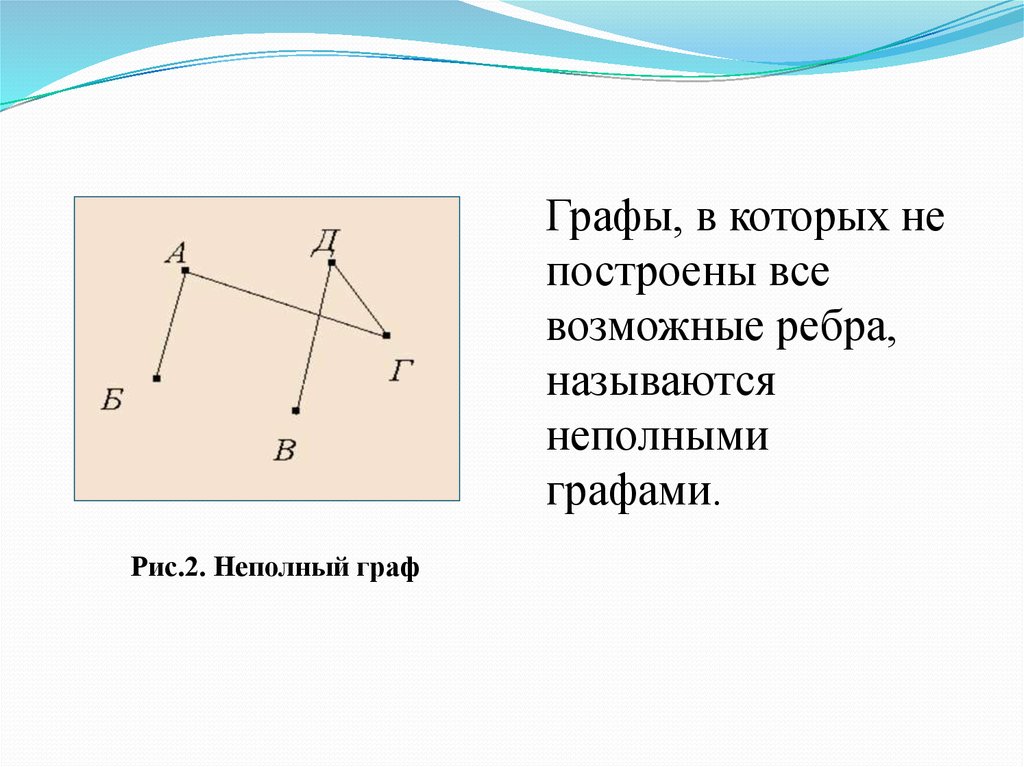
Графы, в которых не
построены все
возможные ребра,
называются
неполными
графами.
Рис.2. Неполный граф

19. Задание. Существует ли полный граф с семью ребрами?

Заметим, что если полный граф имеет n вершин, то
количество ребер равно
n(n-1)/2
Задание. Существует ли полный граф с семью ребрами?
ОТВЕТ
Решение: Зная количество ребер, узнаем количество вершин.
n(n-1)/2=7.
n(n-1)=14.
Заметим, что n и (n-1) – это два последовательных
натуральных числа. Число 14 нельзя представить
в виде произведения двух последовательных натуральных
чисел, значит, данное уравнение не имеет решений.
Следовательно, такого графа не существует.

20. Задание 4. Построить граф по заданному условию:

В соревнованиях по футболу участвуют 6 команд. Каждую из
команд обозначили буквами А, B, C, D, E и F. Через несколько
недель некоторые из команд уже сыграли друг с другом:
A
B
С
D
E
F
с
c
с
с
с
с
C,
C,
A,
A,
B,
A,
D,
E,
B;
E,
D,
B,
F;
F;
ОТВЕТ
F;
F;
D.

21. Изображение графа

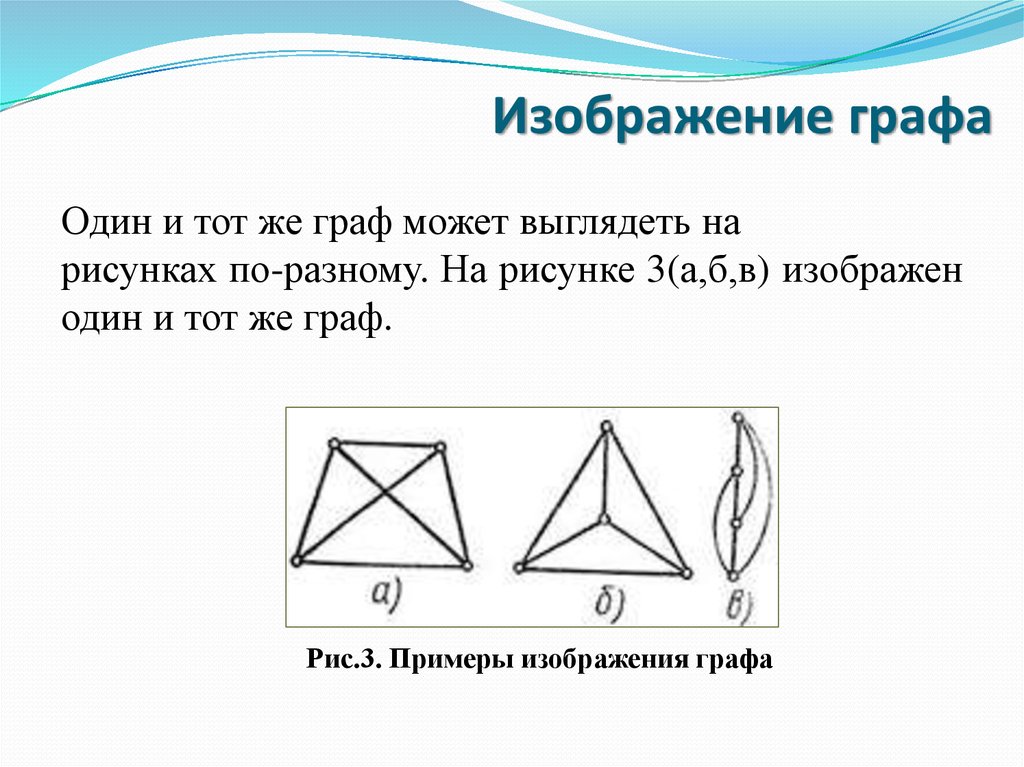
Один и тот же граф может выглядеть на
рисунках по-разному. На рисунке 3(а,б,в) изображен
один и тот же граф.
Рис.3. Примеры изображения графа

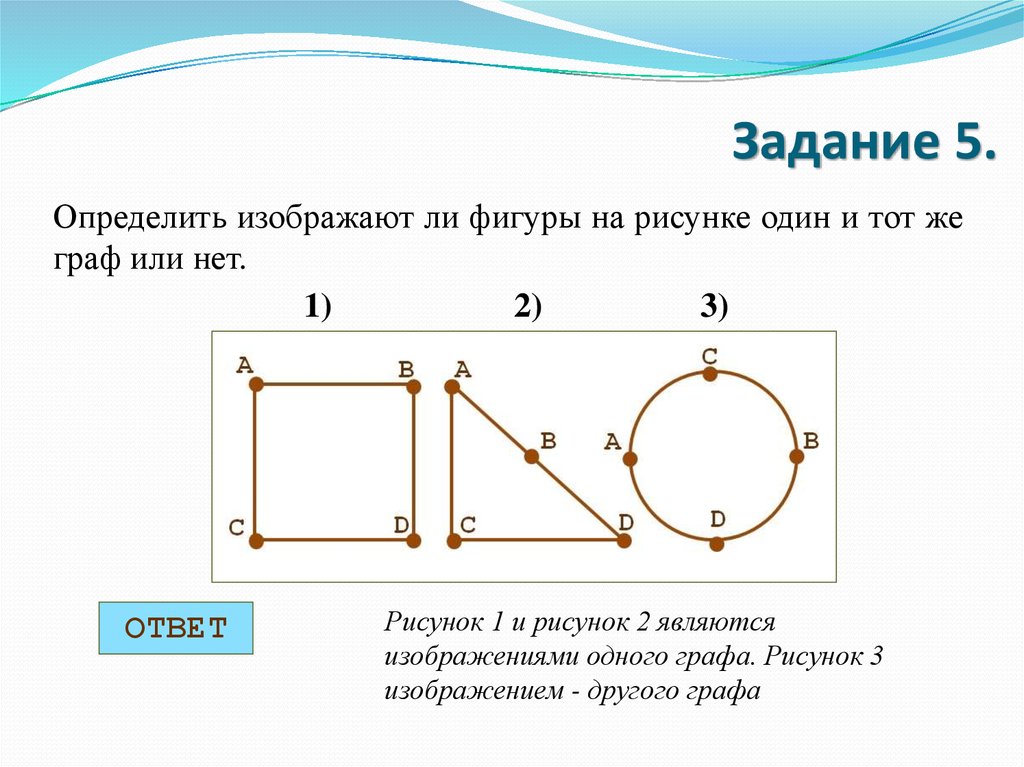
22. Задание 5.

Определить изображают ли фигуры на рисунке один и тот же
граф или нет.
1)
2)
3)
ОТВЕТ
Рисунок 1 и рисунок 2 являются
изображениями одного графа. Рисунок 3
изображением - другого графа

23. Логические задачи

24. Условие задачи

Шахматный турнир проводится по круговой системе,
при которой каждый участник встречается с каждым
ровно один раз, участвуют семь школьников.
Известно, что в настоящий момент:
1) Ваня сыграл шесть партий;
2) Толя сыграл пять партий;
3) Леша и Дима сыграли по три партии;
4) Семен и Илья сыграли по две партии;
5) Женя сыграл одну партию.
Требуется определить:
с кем сыграл Леша.

25.

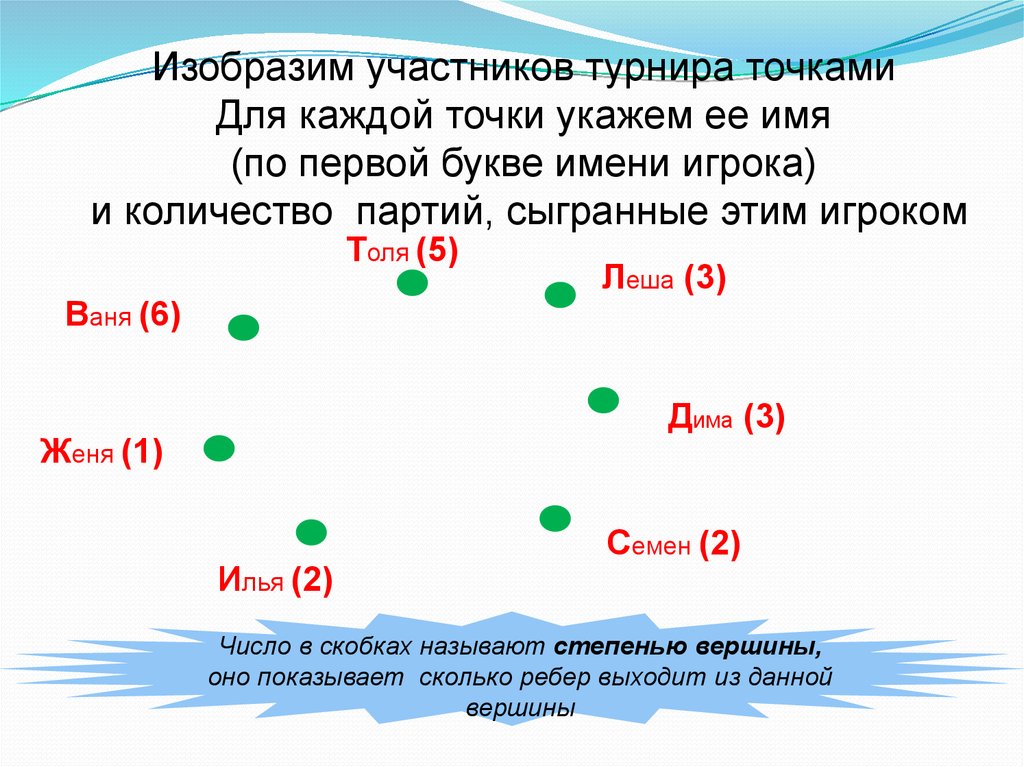
Изобразим участников турнира точками
Для каждой точки укажем ее имя
(по первой букве имени игрока)
и количество партий, сыгранные этим игроком
Толя (5)
Ваня (6)
Леша (3)
Дима (3)
Женя (1)
Илья (2)
Семен (2)
Число в скобках называют степенью вершины,
оно показывает сколько ребер выходит из данной
вершины

26.

Будем строить ребра графа с учетом степеней вершин
Начать построение ребер следует с вершины В,
так как это единственная вершина,
которая соединяется со всеми другими вершинами
графа
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)

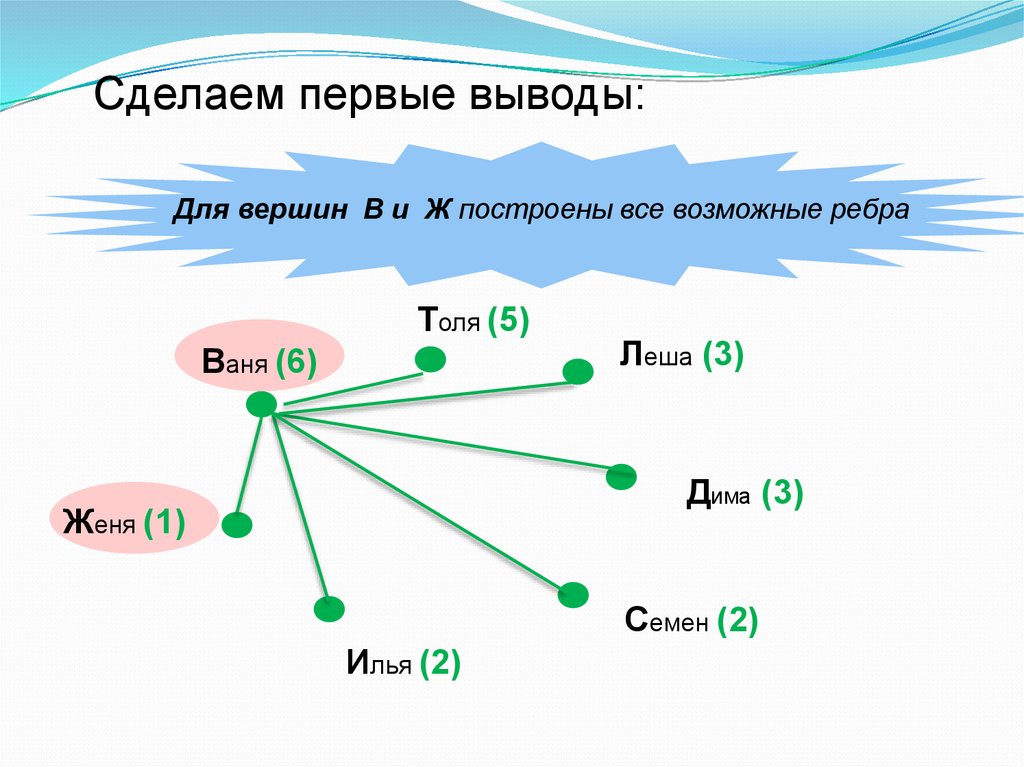
27.

Сделаем первые выводы:
Для вершин В и Ж построены все возможные ребра
Толя (5)
Ваня (6)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)

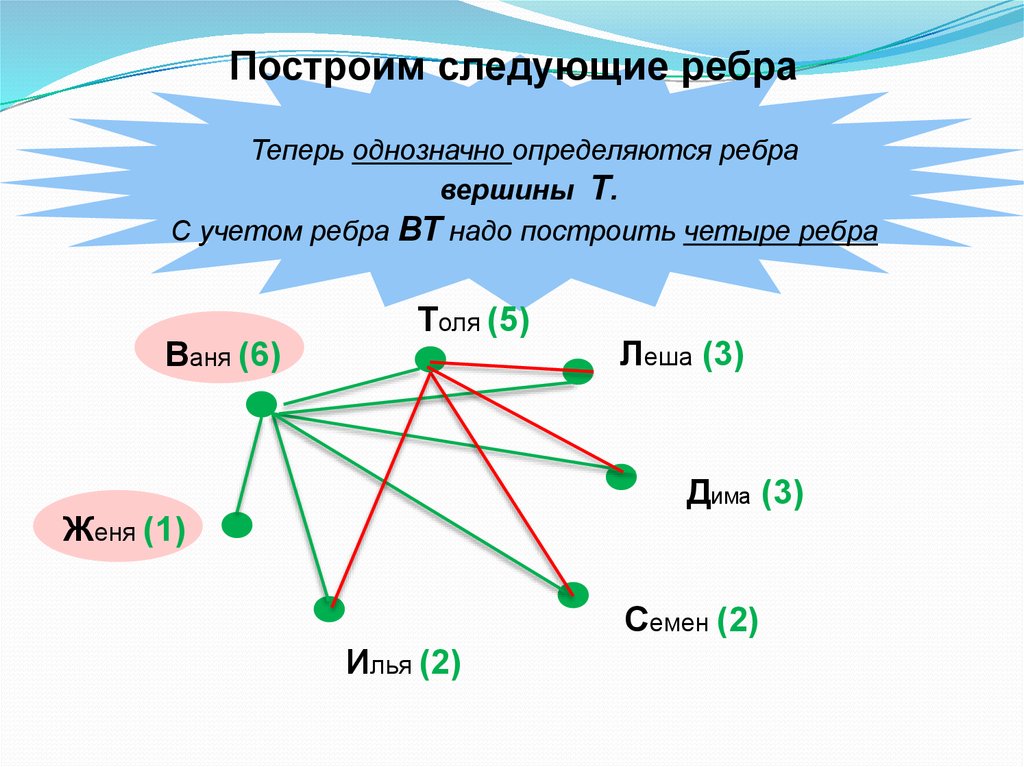
28.

Построим следующие ребра
Теперь однозначно определяются ребра
вершины Т.
С учетом ребра ВТ надо построить четыре ребра
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)

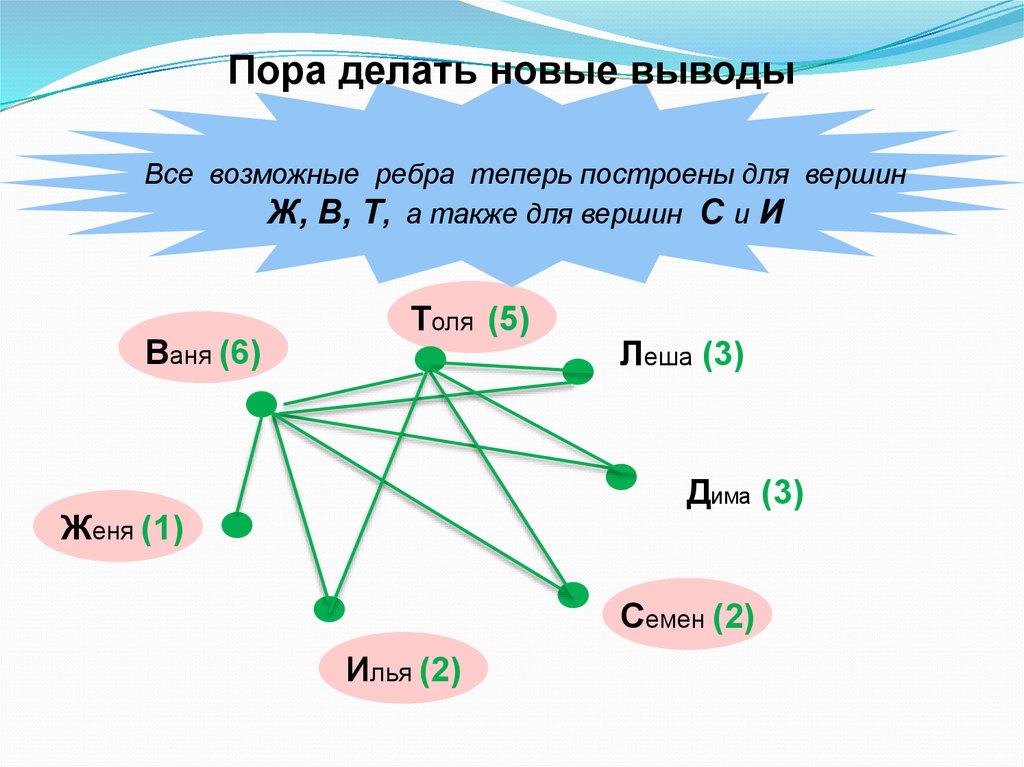
29.

Пора делать новые выводы
Все возможные ребра теперь построены для вершин
Ж, В, Т, а также для вершин С и И
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Женя (1)
Семен (2)
Илья (2)

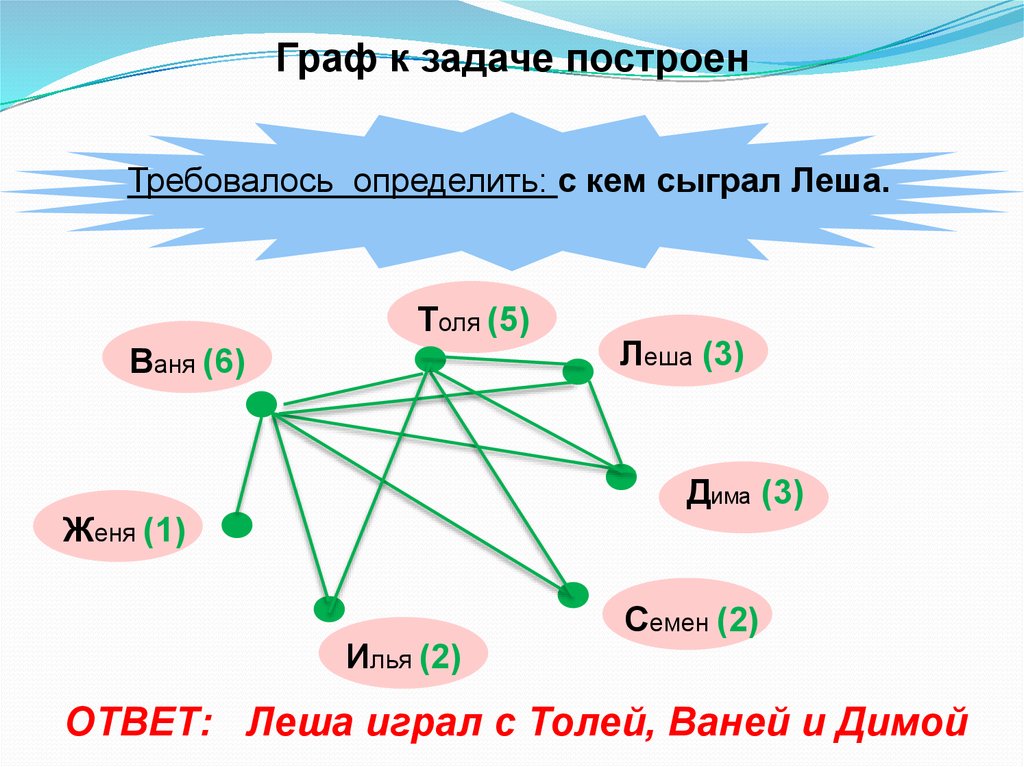
30.

Граф к задаче построен
Требовалось определить: с кем сыграл Леша.
Толя (5)
Ваня (6)
Леша (3)
Дима (3)
Женя (1)
Илья (2)
Семен (2)
ОТВЕТ: Леша играл с Толей, Ваней и Димой

31. Домашнее задание

§1.10.1 стр.112-114.
Выучить все определения.

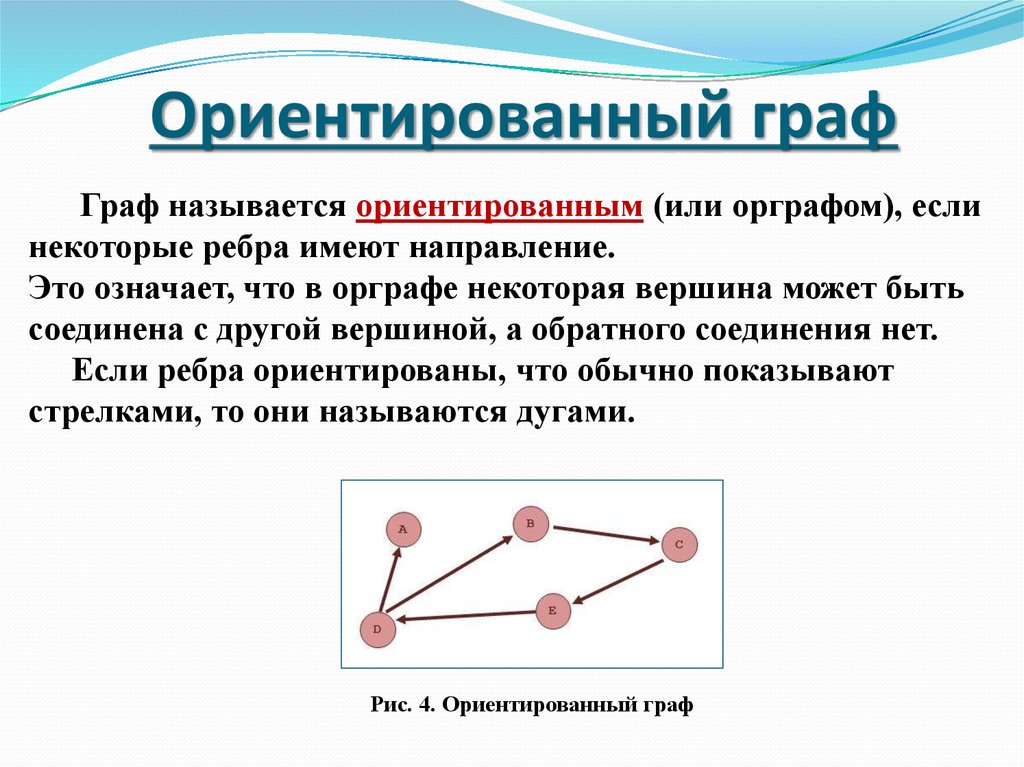
32. Ориентированный граф

Граф называется ориентированным (или орграфом), если
некоторые ребра имеют направление.
Это означает, что в орграфе некоторая вершина может быть
соединена с другой вершиной, а обратного соединения нет.
Если ребра ориентированы, что обычно показывают
стрелками, то они называются дугами.
Рис. 4. Ориентированный граф

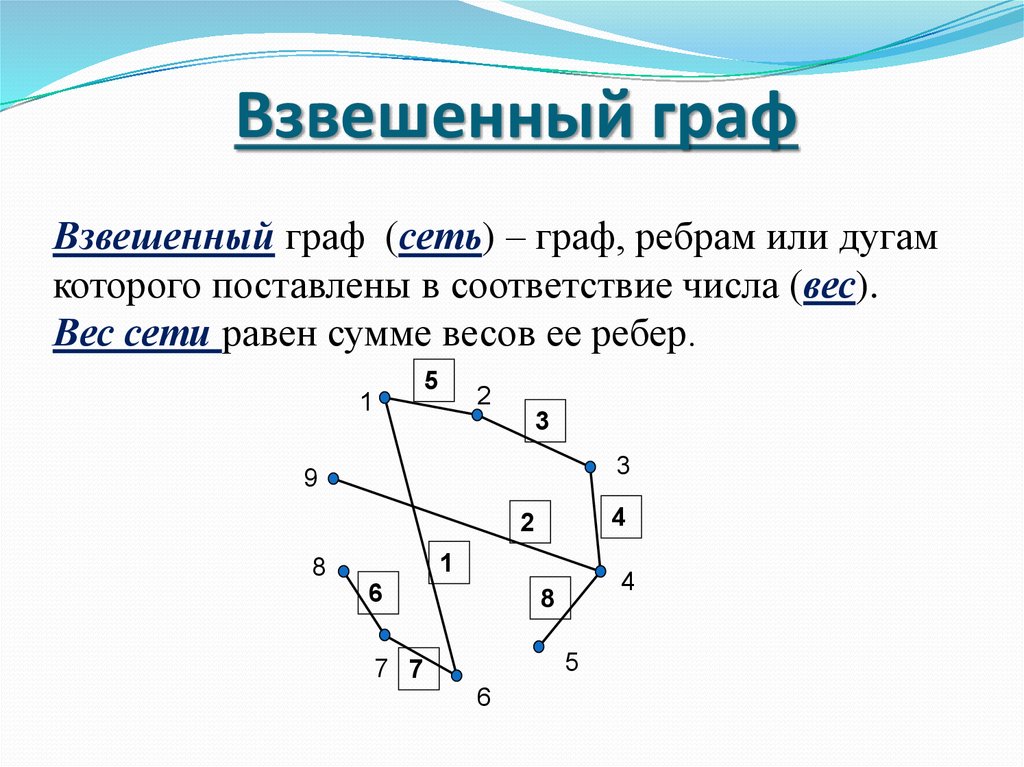
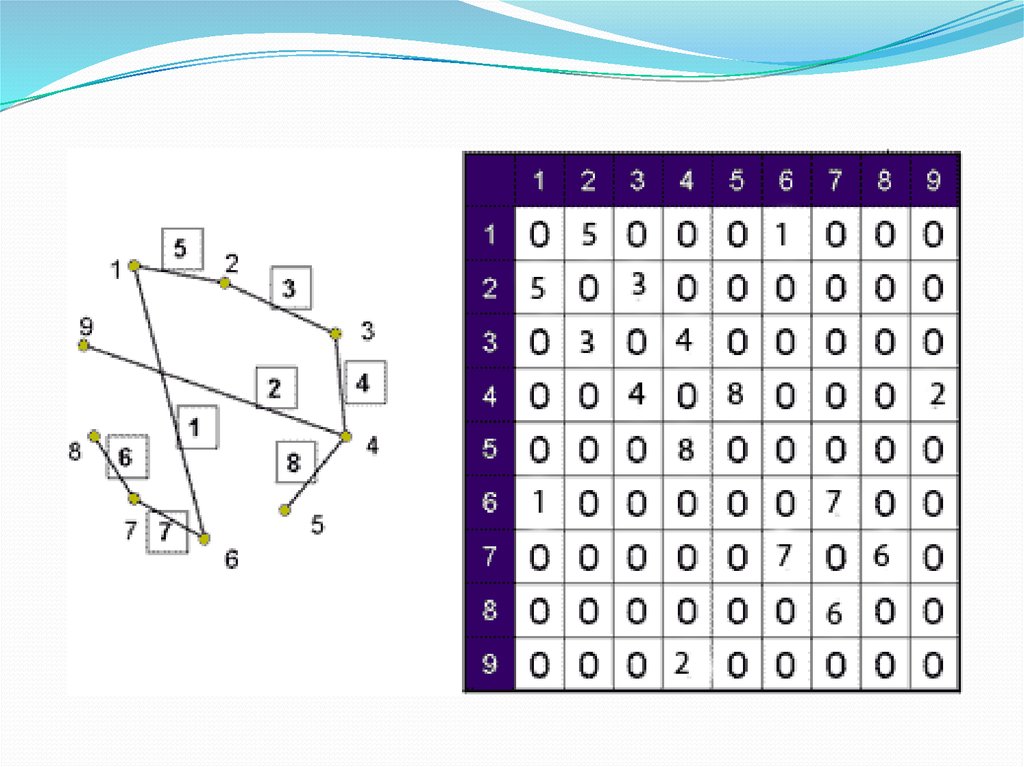
33. Взвешенный граф

Взвешенный граф (сеть) – граф, ребрам или дугам
которого поставлены в соответствие числа (вес).
Вес сети равен сумме весов ее ребер.
5
1
2
3
3
9
4
2
1
8
6
4
8
5
7 7
6

34. Способы описания графа

матрица инциденций,
матрица смежности,
списки связи,
перечни ребер.

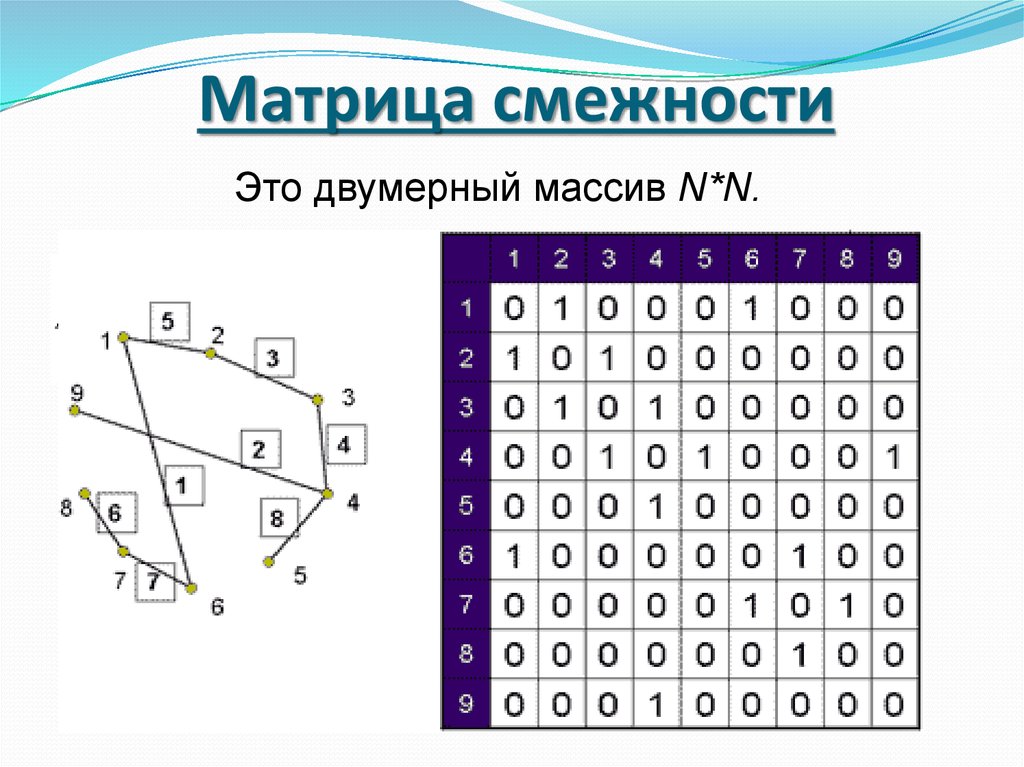
35. Матрица смежности

Это двумерный массив N*N.

36.

37. Домашнее задание

§1.10.1 стр.114-115.
Выучить все определения.
Решить задачи (карточка).