Similar presentations:
Элементарные функции. Гиперболические тангенс и котангенс
1. Элементарные функции
Гиперболические тангенс и котангенсЗадание выполнили:
Шурко Андрей
Турков Виталий
Крикунова Ольга
Плаксин Никита
группа КИ16-09Б
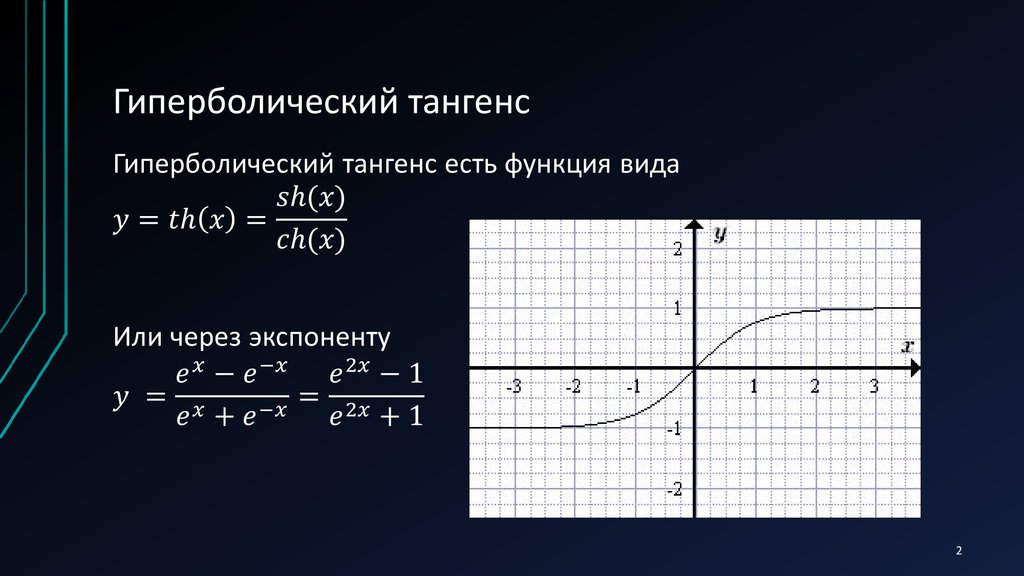
2. Гиперболический тангенс
23. Основные свойства функции y=th(x)
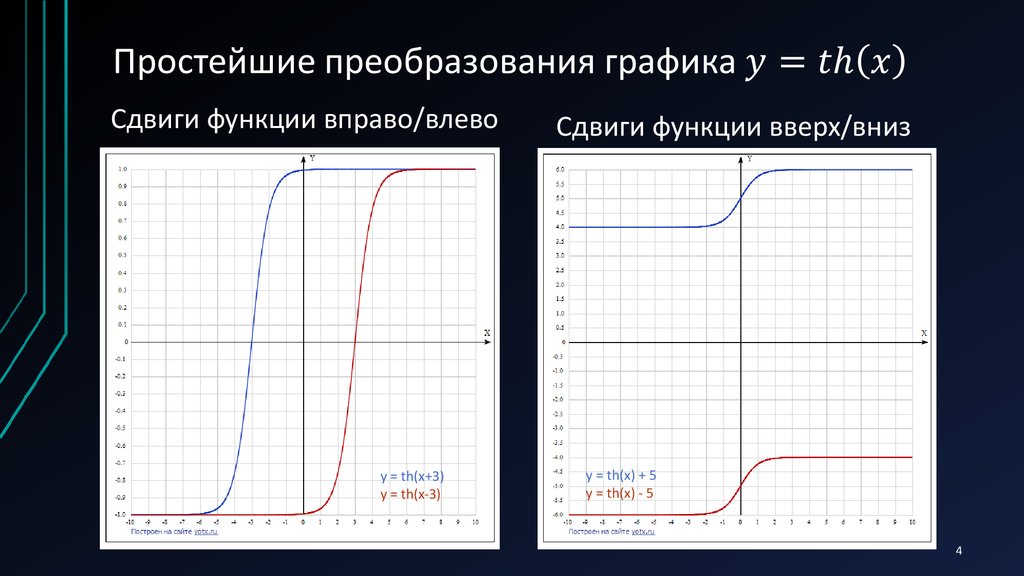
34. Простейшие преобразования графика y=th(x)
Сдвиги функции вправо/влевоy = th(x+3)
y = th(x-3)
Сдвиги функции вверх/вниз
y = th(x) + 5
y = th(x) - 5
4
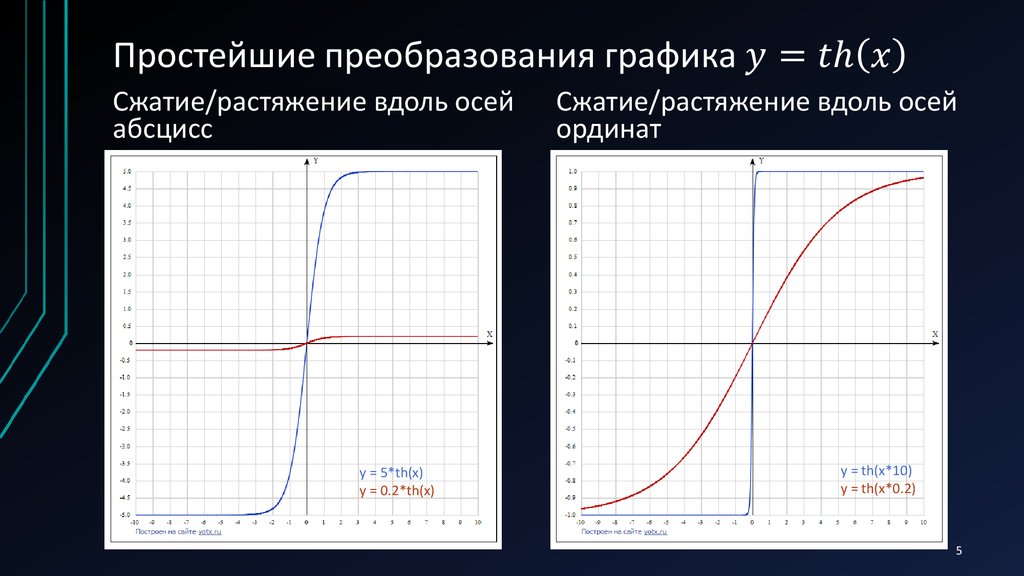
5. Простейшие преобразования графика y=th(x)
Сжатие/растяжение вдоль осейабсцисс
y = 5*th(x)
y = 0.2*th(x)
Сжатие/растяжение вдоль осей
ординат
y = th(x*10)
y = th(x*0.2)
5
6. Простейшие преобразования графика y=th(x)
Отражение относительно координатных осейy = th(-x) = -th(x)
6
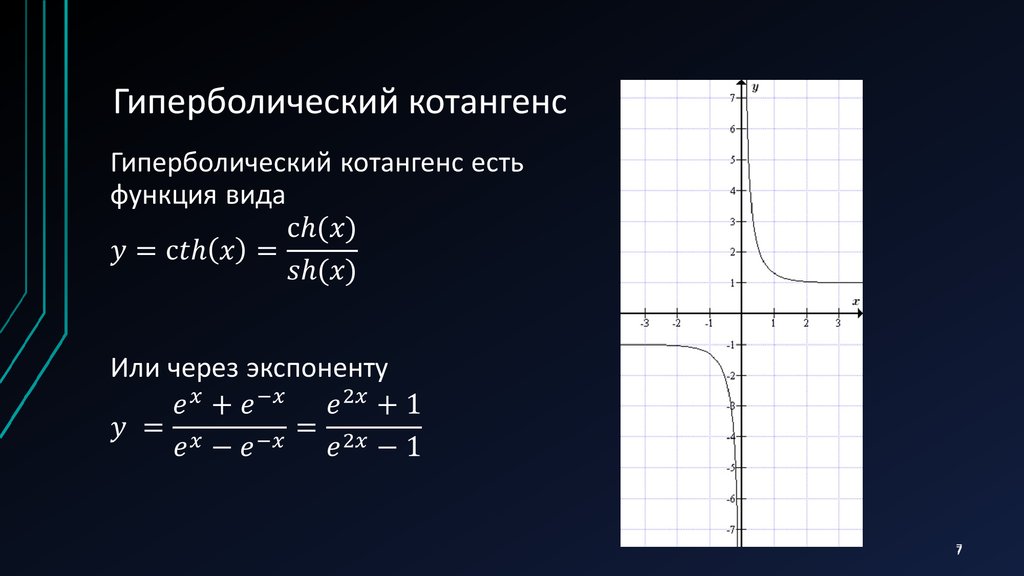
7.
Гиперболический котангенс7
8.
• Область определения D(y)=(-∞;0)ᴜ(0;+∞);• Область значений E(y)=(-∞;-1)ᴜ(1+∞);
• Функция нечетная, т.к. она симметрична относительно
начала координат;
• Функция не периодична;
• Точки пересечения с осями координат: функция не
пересекает оси координат
• Промежутки монотонности: функция убывает на
всей области определения
8
9. Простейшие преобразования графика y=cth(x)
Сдвиги функции вправо/влевоy = cth(x+5)
y = cth(x-5)
Сдвиги функции вверх/вниз
y = cth(x+2)
y = cth(x-1.5)
9
10. Простейшие преобразования графика y=cth(x)
Сжатие/растяжение вдоль осейабсцисс
y = 12*cth(x)
y = 0.2*cth(x)
Сжатие/растяжение вдоль осей
ординат
y = cth(x*20)
y = cth(x*0.1)
10
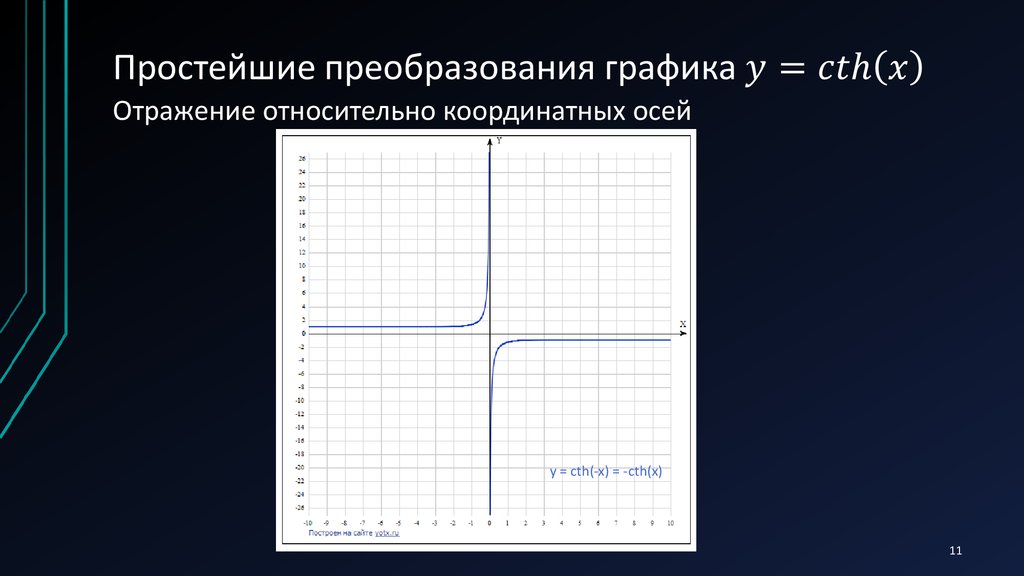
11. Простейшие преобразования графика y=cth(x)
Отражение относительно координатных осейy = cth(-x) = -сth(x)
11
12. Список использованных источников
• https://ru.wikipedia.org/• http://www.yotx.ru/
12









 mathematics
mathematics








