Similar presentations:
Основы тепло- и массопереноса в наземном оборудовании ракетной и ракетно-космической техники
1. Основы тепло- и массопереноса в наземном оборудовании ракетной и ракетно-космической техники
Чугунков В.В.конспект лекций
по дисциплине
Основы тепло- и массопереноса в
наземном оборудовании ракетной
и ракетно-космической техники
Часть 1
Москва 2018
2. Содержание
Основы тепло- и массопереноса в
наземном оборудовании ракетной
и ракетно-космической техники…..1
Основные положения теории
теплообмена………………………….5
Основные виды теплообмена……11
Основные понятия и
определения…………………………16
Виды тепловых потоков……….. …19
Теплопередача через стенки
конструкций при сложном теплообмене на их поверхностях……….32
Теплообмен излучением на
поверхностях конструкций.
Основные законы и определения…………………………………….51
Теплообмен излучением в системе
из нескольких поверхностей……...56
Теплопередача через экранновакуумную изоляцию трубопроводов
заправочных
систем……………………………...…71
Изменение температуры топлива
при движении по трубопроводу от
емкости-хранилища до топливного
бака ракетыносителя…………………………..…89
Теплопередача в конструкциях
емкостей заправочных систем…...93
Определение теплового потока,
поступающего через боковую
поверхность сферической
емкости……………………………….96
Определение теплового потока,
поступающего через опору
емкости……………………………..110
3. Содержание
Теплообмен излучением между
поверхностями конструкций,
произвольно ориентированными в
пространстве……………………....116
Определение средних угловых
коэффициентов облучения в
замкнутой системе поверхностей
теплообмена……………………….121
Примеры определения тепловых
потоков и средних угловых
коэффициентов……………………123
Теплообмен излучением в
замкнутой системе, состоящей из n
поверхностей………………………125
Приближенная оценка с
использованием зависимостей для
теплообмена между телом и
оболочкой…………………………..127
Совместный теплообмен конвекцией и излучением в воздушных
прослойках конструкций…………128
Совместный теплообмен конвекции излучением при термостатировании объектов ракетно-космической
техники……………………………...129
Схема теплообмена при термостатировании (режим обогрева)……131
Определение коэффициентов
теплоотдачи в кольцевом зазоре
между ОТ и ГО…………………….133
Отличия теплообмена для режима
охлаждения………………………137
4. Содержание
Дифференциальные уравнения
тепло- и массоперенос в сплошных средах……………………….144
Условия однозначности ( краевые
условия )…………………………146
Особенности уравнений тепломассопереноса для турбулентных течений……………………..150
Уравнения тепло- и масоопереноса в сплошных средах в
приближениях пограничного
слоя…………………………….153
Условия применимости
уравнений конвективного теплои массопереноса в
приближениях пограничного
слоя………………...158
Условия тройной аналогии
процессов течения и тепломассопереноса……………….161
Пример использования
аналогии между процессами
тепло- и
массопереноса……………….162
5. Основные положения теории теплообмена
• Теория теплообмена – фундаментальная наукаизучающая и устанавливающая взаимосвязь тепловых
потоков и температур при протекании тепловых
процессов
• Функционирование большинства систем и устройств в
технике сопровождается протеканием тепловых
процессов
• Особым многообразием отличается протекание
тепловых процессов в наземном оборудовании ракетной
и ракетно-космической техники, что обусловлено
взаимодействием оборудования с окружающей средой в
периоды транспортировки и предстартовой подготовки
ракет и космических аппаратов, применением
криогенных компонентов топлива, воздействием
струйных потоков горячих газов ракетных двигателей с
поверхностями стартовых устройств в период старта.
6.
• Протекание тепловых процессов в наземном оборудованииобусловлено обеспечением требуемого температурного режима
боевой или космической ракетной системы (РКС) или ее элементов в
процессе наземной подготовки или регламентных испытаний с целью
создания условий для нормального функционирования двигателей,
бортовой аппаратуры, отдельных блоков и систем в целом.
– При транспортировке РКС и боевых ракет их температурный режим должен
находиться в заданных пределах за счет применения специальных
передвижных систем термостатирования, работа которых основана на
организации процессов теплообмена с воздухом (ВСОТР)
•Допустимый интервал температур
КА - +15 ÷ +25 °С
ракет с РДТТ - +5 ÷ 35 (12 ÷ 28) °С
7.
– В период предстартовой подготовки РКС температурный режим ихдвигательных, приборных и головных отсеков должен находиться в
заданных пределах за счет применения специальных стационарных
систем термостатирования, работа которых основана на
организации процессов теплообмена с воздухом (ВСОТР), жидкими
теплоносителями (ЖСОТР) и компонентами топлива (ТСОТР)
8.
– В период боевого дежурства боевых ракет в ШПУ температурныйрежим их двигательных, приборных и головных отсеков должен
находиться в заданных пределах за счет применения специальных
стационарных систем термостатирования, работа которых основана
на организации процессов теплообмена с воздухом (ВСОТР) и
жидкими теплоносителями (ЖСОТР), охлаждающими непрерывно
работающие приборы системы управления
9.
• В период старта ракет протекание процессовтеплообмена обусловлено работой стартовых
ускорителей, двигателей ракет, пороховых
аккумуляторов давления и связано со воздействием
струйных потоков горячих газов с поверхностями
стартовых устройств, пусковых систем и
транспортно-пусковых контейнеров.
10.
• Процессы теплообмена в наземномоборудовании могут сопровождаться
явлениями переноса массы вещества,
которые обусловлены:
– выпадением влаги, находящейся во влажном
воздухе, в жидком (капельном) или твердом
(кристаллобразном) виде при протекании
процессов теплообмена с охлажденными
поверхностями ракетных баков, теплообменных
аппаратов систем термостатирования
– испарением охлаждаемой жидкости в системе
тепловой защиты пусковых устройств от действия
высокотемпературных потоков газов при старте
ракет
– уносом теплозащитных покрытий с
поверхностей стартовых устройств под действием
теплообмена с высокотемпературными потоками
газов в период старта ракет
11. Основные виды теплообмена
• Теплообмен (передача теплоты) можетосуществляться посредством
– теплопроводности
– конвекции
– теплового излучения
• В процессе теплопроводности передача
теплоты происходит за счет непосредственного
соприкосновения элементарных частиц (молекул)
вещества при их тепловом движении.
Теплопроводностью обладают любые твердые
тела, а также жидкие и газообразные среды
12.
• Конвекция представляет процесс переносатеплоты за счет молярного движения жидкости или
газа. Различают процессы естественной
(свободной), вынужденной и смешанной
конвекции.
• При естественной конвекции движение жидкости
или газа происходит за счет разных плотностей
среды в гравитационном поле.
• При вынужденной конвекции движение среды
происходит под действием разности давлений,
создаваемых механическими устройствами
(насосами, вентиляторами) в циркуляционных
контурах систем, а также возникающих в
результате атмосферных явлений (ветер)
• При совместном вынужденном и естественном
движении среды конвекцию принято называть
смешанной
13.
Естественная и смешанная конвекция приводят к тепловому расслоению
топлива в емкостях хранилищах и топливных баках ракеты. Поэтому при
выполнении заправочных операций предусматривается принудительное
перемешивание компонентов топлива
При термостатировании ракет в ТПК смешанная конвекция может приводить к
температурному расслоению воздуха, находящегося вокруг ракеты (в верхней
части сосредотачивается более теплый воздух, в нижней – более холодный)
16
Тd, °C
1- Тн= -43 °C
1
2- Тн= -21 °C
12
2
8
4
x/L
Т
r
14.
• Тепловое излучение является видомпередачи теплоты между телами
посредством электромагнитных волн, для
которого характерно превращение тепловой
энергии в лучистую и, обратно лучистой
энергии в тепловую.
• Лучистая энергия передается с поверхности
тела во все стороны
• Встречая на своем пути другие тела
лучистая энергия ими частично
поглощается, превращаясь в теплоту,
приводящую к нагреву этих тел
15.
• На практике отдельные виды теплообмена в видетеплопроводности, конвекции или теплового
излучения в чистом виде встречаются крайне
редко
• В большинстве случаев один вид теплообмена
сопровождается другими поэтому теплообмен в
этом случае является сложным
• В тепловых расчетах сложные процессы иногда
целесообразно рассматривать как одно целое и
тогда этому процессу присваивают специальное
название. Например, процесс переноса теплоты от
горячей среды к холодной через разделяющую их
стенку принято называть теплопередачей, а
перенос теплоты от движущейся среды к
поверхности конструкции – теплоотдачей.
16. Основные понятия и определения
• Передача теплоты от одного тела к другому или в самомтеле происходит только при наличии разности температур
и направлена в сторону меньшей температуры;
• Теплота как вид энергии (тепловая энергия) измеряется в
джоулях (Дж);
• Количество передаваемой теплоты в единицу времени
называется тепловым потоком Q (Вт) и характеризует
мощность теплового процесса;
• Тепловой поток, проходящий через единицу
теплопередающей поверхности F, перпендикулярной к
направлению потока, называется плотностью теплового
потока (или удельным тепловым потоком) q (Вт/м2)
Q
q
F
(1)
17.
• Температура T является параметром состояния среды и вобщем случае зависит от координат x, y, z изучаемого
пространства и времени
T f ( x, y, z, ) (2)
• Совокупность значений температуры для всех точек
пространства в данный момент времени называется
температурным полем, а уравнение (2) является его
математической формулировкой;
• Если температурное поле изменяется со временем, то оно
является нестационарным (неустановившемся);
• Если распределение температур (температурное поле) не
зависит от времени, то температурное поле называется
стационарным или установившемся;
• Температурное поле может быть функцией трех, двух либо
одной координат. Соответственно оно называется трех-,
двух- и одномерным. Простейшим температурным полем
является одномерное стационарное поле T=f(x) (3)
18.
• Геометрическое место точек , имеющих одинаковую температуру впространстве, образует изотермическую поверхность;
• Изотермические поверхности не могут пересекаться, так как в
одной и той же точке одновременно не может быть двух различных
значений температуры. Они могут быть либо замкнутыми, либо
заканчиваться на границах среды;
• Изменение температуры происходит в направлениях, пересекающих
изотермические поверхности, причем наибольшая интенсивность
изменения температуры происходит в направлении нормали n к
изотермическим поверхностям
n
X
n
X
Т+ T
Т
q
Т– T
T T
n x
T
gradT (4)
n
• Производная температуры по нормали к изотермической поверхности
называется температурным градиентом(gradT), который является
вектором, направленным в сторону повышения температуры. При этом
направление плотности передаваемого теплового потока q
противоположно gradT
19. Виды тепловых потоков
• В расчетах теплообмена в наземномоборудовании приходится принимать во внимание
следующие виды тепловых потоков:
– тепловой поток за счет теплопроводности среды
(qт)
– конвективный тепловой поток (qк)
– тепловой поток за счет фазового перехода
компонентов среды (qф)
– тепловой поток за счет излучения (qл)
– тепловой поток солнечной радиации (qс)
20.
• Тепловые потоки за счет теплопроводности средыопределяются на основании закона Фурье,
устанавливающим прямую пропорциональную зависимость
между плотностью теплового потока qт и температурным
градиентом:
(5)
T
q т
gradT
n
– где – множитель пропорциональности, который называется
коэффициентом теплопроводности, Вт/(м•К), который численно
равен плотности теплового потока при изменении температуры на
1К на расстоянии в 1м
• Коэффициенты теплопроводности различных сред могут
отличаться на несколько порядков и зависят от структуры,
плотности, наличия примесей, влажности, давления и
температуры. В практических расчетах значения
коэффициента теплопроводности определяются по
справочным данным по средней температуре среды
21.
• Конвективный тепловой поток в какой либо точкедвижущейся со скоростью W среде определяется, как
сумма потока за счет теплопроводности среды и ее
движения в определенном направлении, например, в
направлении оси y
Т
q к
Wy cT
y
, (6)
– где плотность среды; с - удельная теплоемкость среды; Wy составляющая скорости движения среды в направлении оси y;
• При конвективном теплообмене между движущейся средой
и поверхностью конструкции конвективный тепловой поток
определяется по формуле Ньютона
q к к (Tf Tw )
, (7)
– где Тf - температура среды; Тw - температура поверхности
конструкции; к - коэффициент пропорциональности, называемый
коэффициентом теплоотдачи конвекцией, Вт/(м2 •К)
22.
• Коэффициент теплоотдачи конвекцией определяетплотность теплового потока, передаваемого от среды к
поверхности конструкции при разности их температур в 1 К;
• Из соотношений (6) и (7) с учетом того, что скорость среды
на поверхности конструкции равна нулю, а производная
температуры на поверхности может быть приближенно
представлена соотношением
T Tw Tf
y
– где - толщина пограничного слоя, прилегающего к поверхности
конструкции, в пределах которого температура среды изменяется от
Тf до Тw
T
Tf Tw
(7)
к
к (Tf Tw )
;
y y 0
• следует, что коэффициент теплоотдачи конвекцией
пропорционален коэффициенту теплопроводности среды и
обратно пропорционален толщине пограничного слоя
23.
• На толщину пограничного слоя , а следовательно и коэффициентатеплоотдачи конвекцией влияет множество факторов:
– форма Ф и размеры Li поверхности конструкции,
– скорость W и физические параметры среды:
• вязкость ,
• плотность ,
• удельная теплоемкость c,
• температурный коэффициент объемного расширения
• Таким образом,
к
i
• Для определения значений к используются результаты
теоретических и в большей части экспериментальных исследований.
• Для распространения результатов исследований на подобные
варианты теплообмена теоретические и особенно экспериментальные
данные представляются с использованием критериев подобия,
являющихся безразмерными параметрами, состоящих из параметров,
характеризующих данный вид теплоотдачи
• Критерии подобия, наиболее часто используемые для определения
коэффициентов теплоотдачи: критерий Нуссельта Nu, критерий
Рейнольдса Re, критерий Прандтля Pr, критерий Грасгофа Gr
f (Ф, L ,W , , , c, ...)
24.
• Nu=αкL/λ – критерий Нуссельта является всегдаопределяемым числом и характеризует интенсивность
конвективного теплообмена на границе жидкость (газ) –
твердое тело;
• Re=wL/ – критерий Рейнольдса является определяющим
числом, характеризует гидродинамический режим
движения жидкости (газа), представляет собой отношение
сил инерции к силам внутреннего трения среды;
• Pr= /a – критерий Прандтля является определяющим
числом, характеризует физические свойства жидкости или
газа (а=λ/ρс – коэффициент температуропроводности);
• Gr=gL3β(Tf –Tw)/ 2 – критерий Грасгофа является
определяющим числом, характеризует подъемные силы
вследствие разности плотностей среды при естественной
конвекции
25.
• В общем случае при конвективном теплообменекритериальная зависимость для определения теплоотдачи
имеет вид
Nu f (Re, Gr , Pr)
– где критерии Re,Gr,Pr являются определяющими критериями, а
критерий Nu – определяемым
• Теплообмен при вынужденном движении среды
определяется критериальным уравнением вида
n
m
Nu c Re Pr
– где с, n, m – постоянные, определяемые теоретически либо
экспериментально
• Для естественной конвекции теплоотдача в критериальном
виде описывается уравнением вида
Nu m c(Gr Pr)
n
m
• Где c,n – экспериментально определяемые величины,
которые зависят от диапазона Gr•Pr. Индекс m
свидетельствует о том, что в качестве определяющей
температуры используется средняя температура между
температурой среды и поверхности конструкции
26.
• тепловой поток за счет фазового переходакомпонентов среды возникает при понижении
температуры среды до температуры фазового
перехода газ – жидкость или газ – твердая фаза.
Данный вид теплового потока возникает, например
при теплообмене влажного воздуха с охлажденными
поверхностями конструкций. При этом находящиеся в
воздухе пары воды могут претерпевать фазовый
переход в пограничном слое либо на самой
поверхности с образованием тумана, конденсата или
инея.
• Плотность теплового потока фазового перехода
определяется зависимостью
q ф m rф
(8)
• Где m кг/(м2с) - плотность потока массы компонента
среды, претерпевающего фазовый переход;
rф Дж/кг – удельная теплота фазового перехода
27.
• Перенос массы вещества в покоящейся средеосуществляется
посредством диффузии, при этом плотность
потока массы m определяется законом Фика
C1
m D
y
(9)
– где D м2/с - коэффициент диффузии вещества в среде;
– С1 кг/м3- концентрация вещества в среде
• При наличии движения среды поток массы вещества
определяется конвекцией
m D
C1
Wy C1
y
• При конвективном массообмене между движущейся средой
и поверхностью конструкции плотность конвективного потока
массы определяется по формуле
m к (C1f C1w ) (10)
– где С1f - концентрация вещества в движущейся среде; С1w концентрация вещества на поверхности конструкции; к коэффициент пропорциональности, называемый коэффициентом
массоотдачи, м/с
28.
• Коэффициент массоотдачи определяет плотность потокамассы вещества, передаваемого от среды к поверхности
конструкции при разности их концентраций в 1 кг/м3 ;
• Из соотношений (9) и (10) с учетом того, что скорость среды
на поверхности конструкции равна нулю, а производная
концентрации на поверхности может быть приближенно
представлена соотношением
C1 C1w C1 f
y
D
– где D- толщина диффузионного пограничного слоя, прилегающего
к поверхности конструкции, в пределах которого концентрация
изменяется от С1f до С1w
D
C1
C1f C1w
(11)
D
к (C1f C1w ) D
;
к
D
D
y y 0
• следует, что коэффициент массоотдачи пропорционален
коэффициенту диффузии и обратно пропорционален
толщине диффузионного пограничного слоя
29.
• Для определения значений к используются результатытеоретических и в большей части экспериментальных
исследований.
• Для распространения результатов исследований на
подобные варианты массообмена теоретические и
особенно экспериментальные данные представляются с
использованием критериев подобия, являющихся
безразмерными параметрами, состоящих из параметров,
характеризующих данный вид массоотдачи
• Критерии подобия, наиболее часто используемые для
определения коэффициентов массоотдачи:
– диффузионный критерий Нуссельта NuD,
– критерий Рейнольдса Re,
– диффузионный критерий Прандтля PrD
Nu D
к L
D
PrD
D
• Критериальное уравнение массоотдачи при вынужденном
движении среды имеет вид
NuD f (Re, PrD )
30.
• тепловой поток за счет излучения (лучистый тепловойпоток) возникает между поверхностью конструкции и ее
окружением при обмене лучистой энергией
• Плотность лучистого теплового потока на поверхности
конструкции, находящейся на открытом пространстве
определяется зависимостью
Tокр 4 T 4
w ,
q л w c0
100 100
– степень черноты поверхности конструкции;
(12)
– где w
– c0=5,67 Вт/(м2К4) – коэффициент излучения абсолютно черного тела;
– Tокр – температура окружения, за которую для поверхностей,
имеющих вертикальную ориентацию, принимается температура
наружного воздуха Tн, а для горизонтальных поверхностей
температура излучения атмосферы Тиа, значения которой может
быть определено по зависимости
Тиа = 1,36 tн + 239, /К/
где tн – температура наружного воздуха, С.
31.
• тепловой поток за счет солнечного излученияскладывается из потоков прямой и рассеянной солнечной
радиации, значения которых зависят от географического
места расположения, времени года, времени суток,
прозрачности атмосферы, ориентации поверхности по
отношению к солнцу
• плотности потока прямого солнечного излучения для
различных географических широт в зависимости от
ориентации поверхности определяются по таблицам
экспериментальных значений солнечной радиации,
имеющихся в справочниках по климату
• для горизонтальной поверхности плотность потока
солнечного излучения приближенно может быть
определена по формуле
sinh
Вт
q c 1360
,
1 p м2
sinh
p
– где h - угол подъема солнца над горизонтом; р - прозрачность
атмосферы
32. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ СТЕНКИ КОНСТРУКЦИЙ ПРИ СЛОЖНОМ ТЕПЛООБМЕНЕ НА ИХ ПОВЕРХНОСТЯХ
33.
• Теплообмен на поверхностях конструкций является, какправило, сложным, когда результирующий тепловой поток
представляет собой совокупность нескольких тепловых
потоков, подводимых к конструкции теплопроводностью,
конвекцией и излучением.
• Характерным примером сложного теплообмена является
теплообмен топливного бака, заполненного криогенным
топливом, в условиях предстартовой
подготовки ракеты.
I
Vв,Тн
3
Схема теплообмена топливного бака
H
qи
I – увеличено
4
5
Аqс
qкв
1
qб
Тн
qкн
dб
2
Тв
II
1- емкость-хранилище криогенного топлива; 2- трубопровод с
экранно-вакуумной изоляцией; 3 – топливный бак; 4 – тепловая
изоляция бака; 5 – стенка бака;
Тw2
Тw0 Тw1
и
б
qф
qл
34.
• Плотность результирующего теплового потока, подводимого кнаружной поверхности топливного бака со стороны окружающей
среды, складывается из плотностей тепловых потоков за счет
конвективного теплообмена с наружным воздухом (qкн), фазового
перехода паров воды, содержащихся в воздухе, на охлажденной
поверхности бака (qф), теплообмена излучением (qл) и солнечной
радиации (qс) и может быть представлена в виде
4
qи
5
Аqс
•qкв
qб
Тн
qкн
(1)
Тв
Тw2
Тw0 Тw1
и
б
q н = qкн + qф + qл + Аqс,
qф
qл
• где А - коэффициент поглощения солнечной радиации для наружной
поверхности топливного бака.
35.
• Плотность конвективного теплового потока за счет теплообменатопливного бака с наружным воздухом при заданной скорости ветра Vв
определяется зависимостями:
4
qи
5
Аqс
q•кв
qб
Тн
qкн
Тв
Тw2
Тw0 Тw1
и
б
qф
qкн = кн (Tн Tw2),
(2)
кн = Nu н / dб ,
(3)
Nu = 0,28 Re 0,6 Prн0,36 (Prн / Prw2)0,25,
(4)
Re = Vв dб / н,
(5)
qл
– где кн - коэффициент теплоотдачи конвекцией на наружной поверхности
бака;
– Tн, Tw2 - температуры наружного воздуха и наружной поверхности бака;
– Nu, Re - числа Нуссельта и Рейнольдса, при определении которых за
характерный размер принимается наружный диаметр бака dб;
– н, н - коэффициенты теплопроводности и кинематической вязкости
наружного воздуха;
– Prн, Prw2 - числа Прандтля для воздуха, определяемые при температурах Tн
и Tw2 соответственно.
36.
Плотность теплового потока за счет фазового перехода паровводы, содержащихся в воздухе, на охлажденной поверхности бака
определяется следующими соотношениями:
qф = ф (Tн Tw2), (6)
ф = rф ф н (dн - dw2) / (Tн Tw2),
(7)
ф = NuD Dн / dб,
(8)
NuD = 0,23 Re0,6, (9)
dн = dнн н,
(10)
– где ф, ф - коэффициенты теплоотдачи и массоотдачи за счет фазового перехода
паров воды, содержащихся в воздухе, на охлажденной поверхности бака;
– rф - скрытая теплота фазового перехода паров воды;
– н, dн, н - плотность, влагосодержание и относительная влажность наружного
воздуха;
– dw2 - влагосодержание воздуха в насыщенном состоянии при температуре наружной
стенки бака Tw2;
– NuD - диффузионное число Нуссельта; Dн - коэффициент диффузии водяных паров;
– dнн - влагосодержание наружного воздуха в насыщенном состоянии при температуре
Tн.
Влагосодержание d = пв/ н (кг/кг) - характеристика влажного воздуха, представляющая
собой отношение плотности (концентрации) паров воды к плотности воздуха.
37.
• Плотность теплового потока за счет теплообмена излучением нанаружной поверхности бака определяется зависимостями:
Tокр 4 T 4
w 2 ,
q л w 2c0
100 100
qл = л (Tн Tw2), (11)
Tокр 4 T 4
w 2
w 2 c 0
100 100
л
,
Tн Tw 2
(12)
• где л – коэффициент теплоотдачи излучением; w2 – степень черноты
наружной поверхности бака; c0 – коэффициент излучения абсолютно
черного тела; Tокр – температура окружения, за которую для
поверхностей, имеющих вертикальную ориентацию, принимается
температура наружного воздуха Tн.
38.
Подстановка зависимостей (2), (6) и (11) в уравнение (1) приводит
его к следующему виду
q н = ( кн + ф + л ) (Tн Tw2) + Аqс.
Использование
понятия
суммарного
(результирующего)
коэффициента теплоотдачи в виде:
н = кн + ф + л
(14)
позволяет представить плотность
результирующего теплового потока на наружной поверхности
топливного бака следующим уравнением
q н
(13)
Aq c
Tw 2
н Tн
н
(15)
Выражение в круглых скобках уравнения (15) обозначим через
Tну(б)
Tну(б) = Tн + Aqc/ н,
(16)
которое назовем “условной температурой” наружного воздуха,
учитывающей воздействие на поверхность бака солнечной
радиации. Соотношение (16) позволяет представить плотность
результирующего теплового потока на наружной поверхности
топливного бака в виде
q н = н ( Тну(б) Тw2 ) .
(17)
39.
• От наружной поверхности бака передача теплоты осуществляетсятеплопроводностью через стенку бака, которую, ввиду малости ее
толщины по сравнению с диметром бака, можно рассматривать
плоской. С учетом данного обстоятельства плотности тепловых потоков
в стенке (qб) и тепловой изоляции (qи) бака описываются
зависимостями
• qб = б (Tw2 Tw1) / б , (18)
qи = и (Tw1 Tw0) / и , (19)
– где б, б - коэффициент теплопроводности и толщина стенки бака;
– и, и - коэффициент теплопроводности и толщина тепловой изоляции бака;
– Tw1, Tw0 - температуры на внутренних поверхностях стенки и тепловой
изоляции бака.
• От внутренней поверхности тепловой изоляции бака теплота
передается топливу посредством свободной конвекции. Плотность
теплового потока, передаваемого топливу в баке, определяется
1
зависимостями
g T T 3
в w0 в
qкв = кв (Tw0 Tв), (20)
кв = 0,15 в
, (21)
a
в в
• где
кв - коэффициент теплоотдачи конвекцией
к топливу,
расположенному в баке; в, в - коэффициент теплопроводности и
температурный коэффициент объемного расширения топлива; в, ав коэффициенты кинематической вязкости и температуропроводности
топлива; Tв - температура топлива в баке; g - ускорение свободного
40.
• При установившемся теплообмене топливного бака с окружающейсредой справедливо равенство плотностей тепловых потоков
q н = qб = qи = qкв = q ,
(22)
• где q - плотность результирующего теплового потока, подводимого к
топливу через стенку бака из окружающей среды.
Сложение уравнений (17), (18), (19) и (20) с учетом равенств (22)
позволяет
получить
зависимости
для
расчета
плотности
результирующего теплового потока, поступающего в бак через его
боковую поверхность, и температур на поверхностях бака
1
к
q = к (Тну(б) Тв), (23)
(24)
1
1
б и
н б и кв
• Тw2 = Tну(б) q / н,
(25)
Тw0 = Tв + q / кв,
• где к – коэффициент теплопередачи стенки бака.
(26)
41.
• Поскольку плотность результирующего теплового потока q зависит оттемператур Тw2 и Тw0, а они в свою очередь определяются q , расчет их
значений проводится методом последовательных приближений.
• Алгоритм расчета плотности результирующего теплового потока,
поступающего через стенку бака из окружающей среды, предполагает
следующую последовательность действий:
– 1. Для заданного значения температуры наружного воздуха Тн по
табличным данным определяются значения коэффициентов
кинематической вязкости ( н),
теплопроводности ( н), числа
Прандтля (Prн), влагосодержания в состоянии насыщения (dнн) и
плотности ( н) для наружного воздуха;
– 2. С использованием зависимостей (5), (4) и (3), определяется
первое приближение для коэффициента теплоотдачи конвекцией на
наружной поверхности бака ( кн) в предположении, что Prн / Prw2 = 1
Re = Vв dб / н,
Nu = 0,28 Re 0,6 Prн0,36 (Prн / Prw2)0,25,
кн = Nu н / dб
42.
• 3. Для первого приближения поскольку неизвестны значениятемператур поверхностей бака задаются значения коэффициентов
теплоотдачи за счет фазового перехода паров воды ( ф) и излучения
( л) на наружной поверхности бака, пологая, например,
» ф = кн ; л = кн;
• 4. Далее задается первое приближение коэффициента теплоотдачи
конвекцией к топливу в баке ( кв), с использованием, например,
равенства
» кв = 100 кн;
• 5. С использованием зависимостей (14) и (16), определяются значения
результирующего коэффициента теплоотдачи на наружной поверхности
бака ( н) и условной температуры наружного воздуха (Tну(б));
» н = кн + ф + л;
Tну(б) = Tн + Aqc/ н
• 6. По зависимостям (24) и (23) определяются значения коэффициента
теплопередачи стенки бака (к) и плотности результирующего теплового
потока, поступающего из окружающей среды (q );
» к
1
б и
1
1
н б и кв
;
q = к (Тну(б) Тв)
43.
• 7. Далее определяются значения температур на поверхностяхбака (Tw2 и Tw0) с использованием зависимостей (25) и (26);
» Тw2 = Tну(б) q / н,
Тw0 = Tв + q / кв,
• 8. По значениям температур Tw2 и Tw0 определяются следующие
приближения для коэффициентов теплоотдачи кн, ф, л и кв с
использованием зависимостей (4), (3), (9), (8), (10) (7), (12) и (21);
– по Tw2 находится значение числа Прандля Prw2, влагосодержания
dw2 , скрытой теплоты фазового перехода rф , далее
»
»
»
»
»
»
Nu = 0,28 Re 0,6 Prн0,36 (Prн / Prw2)0,25,
кн = Nu н / dб
NuD = 0,23 Re0,6,
ф = NuD Dн / dб,
Tокр 4 T 4
w 2
w 2 c 0
dн = dнн н,
100 100
,
ф = rф ф н (dн - dw2) / (Tн Tw2), л
Tн Tw 2
1
g T T 3
в
» кв = 0,15 в в w 0
a
в в
44.
• 9.Далее повторяются действия по п.5,6 и 7 и находятся новыезначения температур на поверхностях бака Tw2н и Tw0н;
» н = кн + ф + л;
»
к
Tну(б) = Tн + Aqc/ н
1
;
б и
1
1
н б и кв
» Тw2н = Tну(б) q / н,
• 10.Полученные
значения
предыдущими значениями.
q = к (Тну(б) Тв)
Тw0н = Tв + q / кв
температур
н
сравниваются
н
– Если Tw 2 Tw 2 0,1
или Tw 0 Tw 0 0,1
средние
значения
между
последующим
приближениям температур поверхностей бака:
Tw2 = 0,5(Tw2 + Tw2н);
с
определяются
и
предыдущим
Tw0 = 0,5(Tw0 + Tw0н),
• после чего повторяются действия по п.8 и 9.
• Расчеты повторяются до тех пор, пока не будут выполняться
условия:
н
н
Tw 0 Tw 0 0,1
» Tw 2 Tw 2 0,1
и
;
45.
• В результате расчетов определяется коэффициент теплопередачистенки бака (к) и плотность результирующего теплового потока,
поступающего через нее к топливу из окружающей среды (q ).
• Результирующий тепловой поток, поступающий через поверхности
бака из окружающей среды, находится по следующей зависимости:
Q = q dбH + 2qдFд,
– где q - плотность результирующего теплового потока, поступающего через
боковую поверхность бака из окружающей среды, значение которой
определяется в соответствии с рассмотренным алгоритмом; dб, H, Fд, –
наружный диаметр, высота и площадь днища бака; qд – плотность
теплового потока, поступающего через днище бака (qд q ).
• Необходимый расход топлива для термостатирования его в топливном
баке ракеты-носителя в период предстартовой подготовки, находится
из уравнения
» Gfв = Q /cfв( Tв max Tв min),
• где cfв – удельная теплоемкость топлива в баке; Tв
и Tв min –
максимальное и минимальное значения температуры топлива в баке:
Tв max = Tв + Tв ;
Tв min = Tв Tв ;
• Tв - допустимое отклонение температуры топлива в баке от ее
заданного значения Tв.
max
46. Для удобства расчетов табличные значения влагосодержания и числа Прандтля могут аппроксимироваться с использованием
експоненциальныхфункций или полиномов в пакете Excel
d (кг/кг)
0.018
0.016
0.014
y = 0.0035e
2
0.0738x
R = 0.9982
-20.00000000000
-10
0
10
20
0.012
0.01
0.008
0.006
0.004
0.002
0
-30.0000 -20.0000 -10.0000 0.00000 10.0000 20.0000 30.0000
0000000 0000000 0000000 000000 0000000 0000000 0000000
0.0008
0.00163
0.00385
0.0074
0.015
0.00080
0.00167
0.00350
0.00732
0.01531
Ряд1
Экспоненциальный
(Ряд1)
47.
d (кг/кг)0.016
y = 1E-08x4 + 2E-07x3 + 5E-06x2 + 0.0003x +
0.0038
0.014
R =1
2
0.012
0.01
0.008
0.006
0.004
0.002
0
-30.00 -20.00 -10.00 0.0000 10.000 20.000 30.000
00000 00000 00000 00000 00000 00000 00000
0000 0000 0000
00
000
000
000
Ряд1
Полиномиальный
(Ряд1)
48. Порядок выполнения аппроксимации
• В таблицы вводятся значения температуры и соответствующиеим значения искомой функции
-20.00000000000
0.721
-10
0.717
0
0.713
10
0.706
20
0.705
• Активизируется значок «Мастер диаграмм» далее
– Точечная
– Далее>(устанавливаются параметры сетка, надписи осей)>Готово
– На любой точке щелчком правой кнопки, а затем левой «Добавить
линию тренда»
– Выбирается тип аппроксимации (линейная, экспоненциальная, и тд.)
и после активизирования кнопки «Параметры» выделяются
«Показать уравнение…» и «Поместить на диаграмму» «Ок»
49.
y = -0.0004x + 0.7124R2 = 0.9671
Ряд1
Линейный (Ряд1)
1
температура град.Цельсия
0.722
0.72
0.718
0.716
0.714
0.712
0.71
0.708
0.706
0.704
0.702
-30.00 -20.00 -10.00 0.0000 10.000 20.000 30.000
00000 00000 00000 00000 00000 00000 00000
0000 0000 0000
00
000
000
000
Числа Прандтля
Числа Прандтля
0.722
0.72
0.718
0.716
0.714
0.712
0.71
0.708
0.706
0.704
0.702
-30.00 -20.00 -10.00 0.000 10.00 20.00 30.00
00000 00000 00000 00000 00000 00000 00000
0000 0000 0000 000 0000 0000 0000
0.722
0.72
0.718
0.716
0.714
0.712
0.71
0.708
0.706
0.704
0.702
-30.00 -20.00 -10.00 0.000 10.00 20.00 30.00
00000 00000 00000 00000 00000 00000 00000
0000 0000 0000 000 0000 0000 0000
y = -0.0004x + 0.7124
R2 = 0.9671
Ряд1
Линейный (Ряд1)
2
температура град.Цельсия
y = 0.7124e-0.0006x
R2 = 0.9669
Ряд1
Экспоненциальный
(Ряд1)
3
1
2
3
-20.00000000000
0.721
0.72040
0.72080
0.721
-10
0.717
0.71640
0.71770
0.716687
0
0.713
0.71240
0.71200
0.7124
10
0.706
0.70840
0.70670
0.708138
20
0.705
0.70440
0.70480
0.703902
50.
• С помощью ППП Excel может быть осуществлен и самрасчет, основанный на задании значений температур на
поверхностях стенки бака Тw0 и Тw2 по следующему
алгоритму:
– Задание исходных данных:
• 1.Параметры бака (Н,dб,δб,λб,εw2,Fд)
• 2.Параметры топлива в баке (Тв,ΔТв, λв, в,св,ρв,βв)
• 3.Параметры окружающей среды (Vв,qс,Тн, н, н, λн,
Prн,Dн, ρн,dнн,rф)
– 4.Задание неизвестных параметров Тw0, Tw2
– 5.Расчет теплопередачи через стенку бака
(Re,Prw2,Nu, кн,dн,dw2,Nud,βф, ф, л,ав, кв, ∑,ТНусл,к,q∑,
Тw0н, Tw2н
Q∑,Gfв
51. Теплообмен излучением на поверхностях конструкций
Основные законы и определения52.
• Поверхности конструкций, температура которых отличнаот абсолютного нуля, обладают способностью излучать в
окружающее пространство лучистую энергию, количество
которой пропорционально четвертой степени
температуры
• В соответствии с законом Стефана-Больцмана плотность
теплового потока собственного излучения поверхности
тела Е определяется уравнением
Е
T
E c 0
100
4
, (1)
– где с0=5,67 Вт/(м2К4) – коэффициент излучения абсолютно черного
тела; ε=с/с0 – степень черноты поверхности; с – коэффициент
излучения данной поверхности, Т, К – температура поверхности
53.
• Плотность потока падающего излучения Епад наповерхность частично ею поглощается с плотностью
поглощенного потока ЕА, частично отражается с
плотностью отраженного потока ЕR, а также может
пропускаться с плотностью пропускаемого потока ЕD
Е
Епад
ЕR
Епад=ЕА+ЕR+ЕD,
ЕD
(2)
ЕA
• Отношения составляющих к плотности потока падающего излучения
принято называть:
ЕА
А - поглощательной способностью
Е пад
ЕR
R - отражательной способностью
Е пад
ЕD
D - пропускательной способностью
Е пад
А+R+D=1, (3)
54.
• Поверхности, у которых поглощательная способность А=1,называются абсолютно черными
• Поверхности с отражательной способностью R=1
называются абсолютно белыми или зеркальными
• Поверхности, у которых пропускательная способность D=1,
называются абсолютно прозрачными или
диатермичными
• Поверхности, у которых пропускательная способность D=0,
являются непрозрачными. Для непрозрачных (серых)
поверхностей
А+R=1, (3)
• Сумма потоков собственного излучения и отраженного
излучения образуют поток эффективного излучения Еэф
Еэф=Е+ЕпадR, (4)
55.
• Плотность результирующего потока излучения дляповерхности, участвующей в лучистом теплообмене,
определяется разностью между плотностями собственного
и поглощенного излучения
qрез=Е-ЕпадА,
(5)
Е пад
E q рез
А А
(6)
• Для непрозрачных поверхностей
qрез=Е-ЕпадА+ЕпадR-ЕпадR=Еэф-Епад, (7)
• Подстановка (6) в (7) приводит к следующим соотношениям
q рез
Е эф
Е q рез
Е эф
А
А
Е
1
q рез 1
А
А
(8)
56. Теплообмен излучением в системе из нескольких поверхностей
• 1) Система из двух плоских бесконечно большихповерхностей
Т1,А1,ε1
Т2,А2,ε2
Е1
Е2R1
Е2
Е1R2
Е1+Е2R1=Еэф1; (9)
Е2+Е1R2=Еэф2; (10)
q12=Еэф1-Еэф2 (11)
1 Е2
Е1
1
q12 q12 1
q 21 1 (12)
А1
А1 А 2
А2
q21=-q12 (13)
q 12
E1
E2
A1
A2
(14)
1
1
1
A1
A2
57.
• Плотности потоков собственного излученияповерхностей
4
T1
E1 1c 0
100
4
T2
E 2 2c0
100
4
q12
T1
T2
1c 0
2c0
100
100
A1
A2
1
1
1
A1 A 2
4
(15)
• По закону Кирхгофа для серых поверхностей Аi=εi (16)
4
4
T
T
Т,А1,ε1
c0
A
c
Е0А1=Е1
1 1 0
100
100
Т,А0
4
Е0А1
Е1
Е0
(16)
(17)
q12
4
T1
T2
100
100
(17)
c0
1
1
1
A1 A 2
58.
• Если ввести понятие приведенной поглощательнойспособности системы из двух II плоскостей A12
1
A12
(18)
1
1
1
A1 A 2
(17)
T1 4 T2 4
q12 c0 A12 (19)
100 100
• По аналогии для серых поверхностей с учетом выполнения
закона Кирхгофа плотность лучистого потока
передаваемого в системе из двух II плоскостей может быть
представлена зависимостью
T1 4 T2 4
q12 c 0 12
(20)
100 100
• где ε12 - приведенная степень черноты системы
1
12
(21)
1 1
1
1 2
ε1, ε2 - степени черноты
поверхностей системы
59.
• Значения А12 (ε12) всегда меньше значений А1, А2 (ε1, ε2).Например, при А1=0,9 и А2=0,7
A12
1
1
1
1
0,9 0,7
0,65
• Для уменьшения лучистого теплообмена достаточно
снизить степень черноты хотя бы одной из поверхностей
путем нанесения покрытия, обладающего низкими
значениями степени черноты. Например,
при А1=0,1 и А2=0,7
1
A12
0,0959
1
1
1
0,1 0,7
при А1=0,1 и А2=0,1
1
A12
0,0526
1
1
1
0,1 0,1
• Другим эффективным способом снижения лучистого
теплообмена является постановка между поверхностями
экранов
60.
• 2) Лучистый теплообмен в системе из двух плоскихбесконечно больших поверхностей при наличии между
T 4 TЭ 4
ними n экранов
1
Т1,А1,ε1
Т2,А2,ε2
q1Э1 c 0 A1Э1
1
100
100
TЭ 4 TЭ 4
q Э1Э 2 c 0 A Э1Э 2 1 2
100
100
(23)
(24)
•••••••••••••••••••••••••
q Эn 2
TЭ 4 T 4
c0 A Э n 2 n 2
100
100
(25)
q1Э1 q Э1Э 2 q Э1 2 q12Э (26)
После сложения (23), (24),…..(25) с учетом равенства (26)
э1
эi
эn
4
4
1
1
1
T1 T2
q12Э
c 0
(27)
А1Э А Э Э
А Эn 2
100 100
1
1 2
61.
• С учетом того, чтоn
1
1
1
1
1
1
1
1
1
1
1
2
1
1
1
1
1
А1Э А Э Э
А
A
A
A
A
A
A
A
A
A
i 1
Эn 2
1
Э1
Э1
Э2
Эn
2
1
2
Эi
1
1 2
1/А12
• соотношение для определения плотности теплового потока
излучением между двумя II поверхностями при наличии
экрана будет иметь вид
q12Э
• где
T1 4 T2 4
c 0 A12Э
100 100
A12Э
1
n
1
2
1
A12 i 1 A Эi
(29)
(28)
62.
• Например, при А1=0,9 и А2=0,7 и одном экране с АЭ=0,1A12Э
1
1
2
1
A12 A Э
1
1
2
1
0,65 0,1
0,0486
• Для сравнения при применении покрытий на поверхностях с Аi=0,1
1
A12
0,0526
1
1
1
0,1 0,1
• т.е. постановка экрана при адекватных значениях Аi=Aэ является более
эффективным способом снижения лучистого потока
• Влияние количества экранов на снижение теплообмена при А1=0,9 и
А2=0,7 и АЭi=0,1
n
0
1
2
3
A12э
0,65
0,0486
0,0253
0,0171
A12i/A12i+1
1
13,37
1,921
1,480
4
0,0129
1,325
63.
• 3) Лучистый теплообмен между телом и егоДля выпуклых серых тел:
оболочкой
Q=EF
QпадR
QпадA
Qпад
2
F2,T2, A2,ε2
F1,T1, A1,ε1
1
Q=EF – поток собственного излучения с
поверхности тела; QпадA, QпадR – соответственно
поглощенная и отраженная составляющие
падающего на тело из вне потока излучения Qпад.
Qрез=Q-QпадА;
Qпад
Q Q рез
A
А
Qрез =Q+QпадR-Qпад (А+R)=Qэф-Qпад;
Q Qрез Q
1
Qэф Qрез
Qрез 1 (30)
A А
A
А
Для системы из выпуклого тела, находящегося внутри замкнутой
оболочки, результирующий тепловой поток, передаваемый от тела
(1) к оболочке (2) определяется уравнением:
Q12=Qэф1φ12- Qэф2φ21, (31)
где φ12 - средний угловой коэффициент облучения телом оболочки;
φ21 - средний угловой коэффициент облучения оболочкой тела
64.
• Средний угловой коэффициент облучения выпуклым теломокружающего пространства всегда равен φ12=1 (это
свойство выпуклого тела)
2
2
1
1
• Средний угловой коэффициент облучения оболочкой тела,
находящегося внутри ее окружающего пространства всегда
меньше 1, т.к. часть лучистого потока попадает на тело, а
часть на поверхность самой оболочки, поэтому
φ21<1
65.
• С учетом того, чтоφ12,=1
_
Q1
1 Q2 _
1
Q12
Q12 1
21 Q21 21 1
A1
A1 A 2
A2
• а Q21=-Q12, результирующий тепловой поток передаваемый
излучением от тела к оболочке будет определяться соотношением (32)
4
Q1 Q 2
T1
Q1 1c0 F1
21
;
A1 A 2
100
(32)
Q12
;
4
1
1
T
1
1 21
1
Q 2 2c0 F2 2 ;
A1
100
A2
• которое с учетом выполнения закона Кирхгофа (А1=ε1 и
А2=ε2) принимает вид
4
4
T
T
1
2
F1
F2
21
100
100
Q12 c 0
; (33)
1 1
21
1
A1
A2
66.
• При Т1=Т2 тепловой поток Q12=0 и из уравнения (33)следует
F1-F2φ21=0;
φ21=F1/F2; (34)
• С учетом соотношения (34) тепловой поток, передаваемый
излучением между телом и его оболочкой, будет
определяться с использованием следующих зависимостей:
T1 4 T2 4
1
;(36)
Q12 c 0 A12 F1
;(35) Где A12
1 F1 1
100 100
1
A1 F2 A 2
A12 – приведенная поглощательная способность системы «тело –
оболочка»; А1,F1 – поглощательная способность и площадь
поверхности тела; А2,F2 – поглощательная способность и площадь
поверхности оболочки;
• При уменьшении зазора между телом и оболочкой F1
и соотношения (35,36) становятся аналогичными
зависимостям при теплообмене двух II поверхностей
F2
67.
• По аналогии для серых поверхностей с учетом выполнения законаКирхгофа лучистый поток, передаваемый в системе, состоящей из
тела и его оболочки, может быть представлен зависимостью
T1 4 T2 4
Q12 c0ε12F1
;(37)
100 100
Где ε12
1
;(38)
1 F1 1
1
ε1 F2 ε 2
ε12 – приведенная степень черноты системы «тело – оболочка»; ε 1,F1
– степень черноты и площадь поверхности тела; ε 2,F2 – степень
черноты и площадь поверхности оболочки;
• Соотношения (35-38) используются для расчетов теплообмена:
– при термостатировании ракеты внутри ТПК или пусковой шахты;
– при термостатировании КА, находящегося под головным обтекателем РН
68.
• 4) Лучистый теплообмен между телом и его оболочкой приналичии между ними экранов
• Для уменьшения лучистого теплообмена в системе тело-оболочка
могут применяться покрытия с низкими значениями степени черноты
(листовой алюминий, алюминиевая фольга, алюминиевая краска) либо
экран (экраны, размещаемые между телом и его оболочкой).
• При наличии экрана тепловые потоки, передаваемые от тела к экрану
Q1Э и от экрана к оболочке QЭ2, определяются зависимостями
Э
T1 4 TЭ 4
Q1Э c0 A1Э F1
;(39)
100 100
TЭ 4 T2 4
QЭ2 c 0 A 2Э FЭ
;(40)
100 100
Q1Э=QЭ2=Q12э;(41)
2
1
• После сложения (39) и (40) с учетом (41) результирующие соотношение
для определения теплового потока в системе тело-экран-оболочка
4
4
будет иметь вид
Q12э
T1 T2
c0 A12Э F1
;(42)
100 100
69.
• В уравнении (41) А12э – приведенная поглощательная способностьсистемы при наличии экрана определяется зависимостью
A12Э
1
;(43)
1
F1 2
1
A12 FЭ A Э
• Где А12 – приведенная поглощательная способность системы без
экрана; Аэ,Fэ – поглощательная способность и площадь поверхности
экрана
• Для более эффективного снижения теплового потока экран выгоднее
располагать ближе к поверхности тела
• При наличии нескольких экранов приведенная поглощательная
способность системы определяется соотношением
A12Э
1
n
1
F1
A12 i 1 FЭi
• где n – количество экранов в системе
2
1
A
Эi
;(44)
70.
• Соотношения (42 – 44) используются врасчетах теплообмена в эранновакуумной изоляции трубопроводов и
емкостей-хранилищ криогенных
компонентов топлив
71. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ЭКРАННО-ВАКУУМНУЮ ИЗОЛЯЦИЮ ТРУБОПРОВОДОВ ЗАПРАВОЧНЫХ СИСТЕМ
72.
• В процессе предстартовой подготовки ракет-носителей, двигателикоторых работают на криогенных компонентах топлива, заправка и
подпитка баков ракеты, а также термостатирование в них криогенных
жидкостей осуществляется при подаче компонентов по
трубопроводам, имеющим экранно-вакуумную изоляцию.
• Трубопровод имеет внутреннюю и внешнюю трубы, пространство
между которыми заполнено коаксиальными экранами и
отвакуумировано вакуум-насосной системой.
I
II - увеличено
Vв,Тн
3
qLн
H
qL2 qLе
qL1
qLкв
1
в
d3
d2
d4
d1
2
4
5
II
7
6
1- емкость-хранилище криогенного топлива; 2- трубопровод с экранно-вакуумной изоляцией;
3 – топливный бак; 4 – внутренняя труба; 5 – экраны; 6–внешняя труба; 7 – вакуумная
прослойка.
73.
• Для расчета теплопритоков к криогенной жидкости, протекающей потрубопроводу с экранно-вакуумной изоляцией, рассмотрим
теплопередачу на его элементарной длине dХ.
qLн
qL2 qLе
qL1
qLкв
в
d3
d2
d4
d1
4
5
7
6
Введем понятие линейной плотности
теплового потока через поверхности
трубопровода, которая определяется
отношением теплового потока Q к длине
трубопровода L
qL=Q/L (1)
• Линейная плотность результирующего теплового потока, подводимого к
наружной поверхности внешней трубы из окружающей среды,
складывается из плотностей тепловых потоков за счет конвективного
теплообмена с наружным воздухом (qкн), фазового перехода паров
воды, содержащихся в воздухе, на охлажденной поверхности
трубопровода (qф), теплообмена излучением (qл) и солнечной
радиации (qс) и может быть представлена в виде
qLн = d4(qкн + qф + qл + А4qс), (2)
– где d4, А4 – диаметр и поглощательная способность наружной поверхности
трубопровода.
74.
• При использовании понятий результирующегокоэффициента теплоотдачи и условной температуры
наружного воздуха в виде
н(т)= кн(т)+ ф(т)+ л(т),(3)
Tну(т)=Tн+ A4qc/ н(т) (4)
qLн может быть представлена следующим образом
qLн = d4 н(т) (Тну(т) Т4), (5)
– где Т4 – температура наружной поверхности трубопровода, а для
определения коэффициентов теплоотдачи кн(т) , ф(т) и л(т)
используются зависимости, в которых в качестве характерного
размера используется наружный диаметр трубопровода d4, а
значения числа Прандтля Pr4 и влагосодержания воздуха dв4
определяются в соответствии с температурой Т4:
кн(т) = Nu(т) н / d4 , (6)
Re(т) = Vв d4 / н, (7)
Nu(т) = 0,28 Re(т) 0,6 Prн0,36 (Prн / Pr4)0,25, (8)
75.
ф(т) = rф ф(т) н (dн – dв4) / (Tн T4), (9)ф(т) = NuD(т) Dн / d4, (10)
NuD(т) = 0,23 Re(т)0,6, (11)
л (Т )
Tокр 4 T 4
4
4c0
100 100
Tн T4
(12)
– где 4 - степень черноты наружной поверхности трубопровода, Токр температура окружения, определяемая как средняя температура
между температурой наружного воздуха и температурой излучения
атмосферы
Токр = 0,5 (Тн + Тиа) , (13) Тиа = 1,36 tн + 239, /К/ (14)
где tн – температура наружного воздуха, С.
76.
• Линейная плотность теплового потока, передаваемоготеплопроводностью через стенку внешней трубы, определяется
соотношением
(T T )
q L2
4
3
d4
ln
2 2 d 3
1
, (15)
– где Т3 – температура на внутренней поверхности внешней трубы; 2 –
коэффициент теплопроводности внешней трубы; d3 и d4 – внутренний и
внешний диаметры внешней трубы.
• Линейная плотность теплового потока, передаваемого излучением
между внешней и внутренней трубой через систему экранов,
определяется соотношениями для теплообмена излучением между
телом и его оболочкой при наличии между ними экранов:
q Le
2,3
э
T2 4 T3 4
c 0 2,3Э d 2
L
100
100
Q 2,3Э
1
1
2,3
d2
i 1 d эi
n
2
1
эi
(17)
2,3
(16)
1
1 d2 1
1
2 d3 3
(18)
77.
• Используя коэффициент теплоотдачи излучением междувнешней и внутренней трубой через систему экранов ( лэ)
соотношение для qлэ может быть представлено в виде
q Le d 2 лэ (Т 3 Т 2 )
лэ
Т 3 4 Т 2 4
2,3э с 0
100
100
Т3 Т2
(19)
(20)
• В формулах (16-20) d2 – наружный диаметр внутренней трубы; лэ –
коэффициент теплоотдачи излучением между внешней и внутренней
трубой через систему экранов; Т2 – температура наружной поверхности
внутренней трубы; - приведенная степень черноты системы с учетом
наличия экранов; - приведенная степень черноты системы без экранов;
dэi, эi – диаметр и степень черноты i-ого экрана; n – количество экранов
в системе; 2, 3 – степени черноты наружной поверхности внутренней
трубы и внутренней поверхности наружной трубы соответственно.
78.
• Линейная плотность теплового потока, передаваемоготеплопроводностью через стенку внутренней трубы,
определяется соотношением
q L1
(T2 T1 )
d2
1
ln
2 1 d 1
,(21)
– где Т1 – температура на внутренней поверхности внутренней трубы;
1 – коэффициент теплопроводности внутренней трубы; d1 –
внутренний диаметр внутренней трубы.
• Линейная плотность теплового потока, передаваемого
конвекцией топливу от внутренней трубы, определяется
зависимостью
qLкв = d1 кв(т) (Т1- Тfв); (22)
– где Тfв – местная температура топлива внутри трубы; кв(т) –
коэффициент теплоотдачи конвекцией топливу от внутренней
трубы
79.
• значения кв(т) для турбулентного режима теченияопределяются зависимостями:
кв (Т )
Nud1 fв
(23)
d1
0,8
0, 43
Nud1 0,021 Re d1 Pr fв
Re d1
4G fв
d 1 fв fв
(24)
(25)
• где - Nu d1 , Re d1 числа Нуссельта и Рейнольдса, при
определении которых за характерный размер принимается
диаметр внутренней трубы d1; fв, fв, fв – плотность,
теплопроводность и кинематическая вязкость топлива; Prfв число Прандтля для топлива; Gfв – массовый расход
топлива, движущегося в трубопроводе.
80.
• При установившемся теплообмене трубопровода с окружающей средойсправедливо равенство линейных плотностей тепловых потоков
qLн = qL2 = qLe = qL1 = qLкв = qL,
(26)
• где qL – линейная плотность результирующего теплового потока,
подводимого к топливу через стенку трубопровода из окружающей
среды.
• Сложение уравнений (15), (19), (21), (22) и (26) с учетом равенств (26)
позволяет получить зависимости для расчета линейной плотности
результирующего теплового потока, подводимого к топливу через
стенку трубопровода с экранно-вакуумной изоляцией, и температур на
поверхностях трубопровода
qL = кL (Тну(т) Тfв),
(27)
– где кL – линейный коэффициент теплопередачи стенки
трубопровода
кL
1
1
d4
1
1
d2
1
ln
ln
н (Т ) d 4 2 2 d3 лэd 2 2 1 d1 кв (Т ) d1
(28)
81.
• Температуры на поверхностях внутренней и наружнойтрубы
qL
T1 T fв
d1 кв
T4 Tну (Т )
qL
d2
T2 T1
ln
2 1 d1
(29)
qL
н (Т ) d 4
(31)
(30)
qL
d4
T3 T4
ln
2 2 d 3
(32)
• Поскольку линейная плотность теплового потока qL зависит
от температур T1 T4, а они в свою очередь определяются
qL, расчет их значений проводится методом
последовательных приближений.
82.
Алгоритм расчета линейной плотности результирующего
теплового
потока,
поступающего
через
стенку
трубопровода с экранно-вакуумной изоляцией из
окружающей
среды,
предполагает
следующую
последовательность действий:
–
–
1. Для заданного значения температуры наружного воздуха по
табличным данным определяются значения коэффициентов
кинематической вязкости ( н), теплопроводности ( н) и числа
Прандтля (Prн) для наружного воздуха;
2. С использованием зависимостей (7), (8) и (6), определяется
первое приближение для коэффициента теплоотдачи конвекцией
на наружной поверхности трубопровода ( кн(т)) в предположении,
что Prн / Pr4 = 1;
Re(т) = Vв d4 / н
Nu(т) = 0,28 Re(т) 0,6 Prн0,36 (Prн / Pr4)0,25
кн(т) = Nu(т) н / d4
83.
–3.Для первого приближения, поскольку неизвестны значения
температур поверхностей трубопровода, задаются значения
коэффициентов теплоотдачи за счет фазового перехода паров
воды ( ф(т)) и излучения ( л(т)) на наружной поверхности
трубопровода, пологая, например,
• ф(т) = 0 и л(т) = кн(т);
–
2,3
4.Определяется первое приближение для коэффициента
теплоотдачи излучением между внешней и внутренней трубой
через систему экранов ( лэ) с использованием соотношений (18),
(17) и (20) и, в предположении, что Т3=Тн,, Т2=Тfв=Tв min;
1
1 d2 1
1
2 d3 3
лэ
2,3Э
1
n
d2
2,3 i 1 d эi
Т 3 4 Т 2 4
2,3э с 0
100
100
Т3 Т2
1
2
1
эi
84.
–5.С использованием зависимостей (25), (24), (23) и значения
расхода топлива Gfв, движущегося по трубопроводу,
определяется коэффициент теплоотдачи конвекцией к топливу
от внутренней трубы ( кв(т)) ;
Re d1
4G fв
d 1 fв fв
Nud1 0,021 Re Pr
Nud fв
кв (Т )
0,8
d1
0, 43
fв
1
–
d1
6. С использованием зависимостей (28) и (29) определяются
значения результирующего коэффициента теплоотдачи н(т) и
условной температуры наружного воздуха Tну(т) для наружной
поверхности трубопровода;
н(т)= кн(т)+ ф(т)+ л(т),
Tну(т)=Tн+ A4qc/ н(т)
85.
–7.По зависимостям (28) и (27) находятся значения линейного
коэффициента теплопередачи трубопровода (кL) и линейной
плотности результирующего теплового потока, поступающего
через его стенку из окружающей среды (qL);
кL
1
1
d4
1
1
d2
1
ln
ln
н (Т ) d 4 2 2 d3 лэd 2 2 1 d1 кв (Т ) d1
qL = кL (Тну(т) Тfв),
–
8.Определяются значения температур на поверхностях
трубопровода (T4, Т3, Т1и T2) с использованием зависимостей (29 32);
qL
T1 T fв
d1 кв
qL
T4 Tну (Т )
н (Т ) d 4
qL
d2
T2 T1
ln
2 1 d1
qL
d4
T3 T4
ln
2 2 d 3
86.
––
–
–
9.По значению температуры T4 определяются следующие
приближения для коэффициентов теплоотдачи кн(т), ф(т) и л(т)
используя зависимостей (8), (6), (9), и (12).
Примечание. При значениях температуры поверхности
трубопровода Т4 Тн коэффициент теплоотдачи за счет
фазового перехода паров воды ф(т) может оказаться
отрицательным, что противоречит физическому смыслу.
Поэтому в этом случае следует полагать ф(т)=0;
10.По значениям температур Т3 и Т2 уточняется коэффициент
теплоотдачи излучением между внешней и внутренней трубой
через систему экранов ( лэ) с использованием соотношения (20);
11.Повторяются действия по п.6,7 и 8 и находятся новые значения
температур на поверхностях трубопровода T4н, T3н, T1н и T2н;
12.Сравниваются полученные значения температур с
предыдущими значениями. Если выполняется хотя бы одно из
следующих неравенств:
н
T4 T4 0,1
н
T3 T3 0,1
н
T2 T2 0,1
н
T1 T1 0,1
Повторяются действия по п.9, 10, 11 и 12 до тех пор пока
последующие и предыдущие значения не будут отличаться на
0,1 К
87. Для удобства расчетов табличные значения числа Прандтля (а при необходимости и влагосодержания) могут аппроксимироваться с
Числа ПрандтляДля удобства расчетов табличные значения числа Прандтля (а
при необходимости и влагосодержания) могут аппроксимироваться
с использованием экспоненциальных фунукций или полиномов в
пакете Excel
0.722
0.72
0.718
0.716
0.714
0.712
0.71
0.708
0.706
0.704
0.702
-30.00 -20.00 -10.00 0.000 10.00 20.00 30.00
00000 00000 00000 00000 00000 00000 00000
0000 0000 0000 000 0000 0000 0000
температура град.Цельсия
y = -0.0004x + 0.7124
R2 = 0.9671
Ряд1
Линейный (Ряд1)
88.
• С помощью ППП Excel может быть осуществлен и самрасчет, основанный на задании значений температур на
поверхностях внутренней и внешней труб Т1,Т2,Т3 и Т4 по
следующему алгоритму:
– Задание исходных данных:
• 1.Параметры трубопровода (d1,d2,d3,d4,dЭi,λ1,λ2,εi)
• 2.Параметры топлива в трубопроводе (Gfв,Тв,ΔТв,
λв, в,св,ρв,βв)
• 3.Параметры окружающей среды (Vв,qс,Тн, н, н, λн,
Prн,Dн, ρн,dнн,rф)
– 4.Задание неизвестных параметров Т1,T2,Т3,T4
– 5.Расчет теплопередачи через стенку
трубопровода (Re(т),Pr4,Nu, кн(т),dн,d4, ф, л(т), ле,
ав, кв(т), ∑н(т),ТНусл(т),кL,qL, Т1н,T2н,Т3н,T4н
89. ИЗМЕНЕНИЕ ТЕМПЕРАТУРЫ ТОПЛИВА ПРИ ДВИЖЕНИИ ПО ТРУБОПРОВОДУ ОТ ЕМКОСТИ-ХРАНИЛИЩА ДО ТОПЛИВНОГО БАКА РАКЕТЫ-НОСИТЕЛЯ
• При заправке топливного бака ракеты-носителя в процесседвижения топлива по трубопроводу от емкости-хранилища
до топливного бака ракеты-носителя происходит изменение
его температуры вследствие теплообмена с окружающей
средой и трения о внутреннюю поверхность трубопровода.
• Для определения зависимостей, определяющих изменение
температуры топлива при движении по трубопроводу,
используется уравнение теплового баланса для
элементарного участка длины трубопровода dx:
k L Tну (Т ) Т fв dx qТР dx G fвc fв dT fв
(33)
где qтр – линейная плотность теплового потока, подводимого к топливу за счет
трения о внутреннюю поверхность трубопровода.
90.
• величина линейной плотности теплового потока за счеттрения определяется следующими зависимостями:
2
4G fв
w
G
P
L
QТР
fв ср
fв
ТР
(37)
(36);wср
qТР
(34); QТР
(35); PТР
2
d1 2
fв d1
fв
L
• где Qтр – тепловой поток, подводимый к топливу за счет
трения; L – длина трубопровода; Ртр – потери давления на
преодоление сил трения; fв – плотность топлива; d1 –
внутренний диаметр трубопровода; wср – средняя скорость
течения топлива по трубопроводу; - коэффициент
сопротивления трения, величина которого для
гидравлически гладких труб и турбулентного режима
движения топлива в диапазоне значений числа Рейнольдса
(3 103 10 8) определяется зависимостью
1
(38);
2
1,82 lg Re d1 1,64
91.
• С учетом уравнений (33)-(38) линейная плотностьтеплового потока, подводимого к топливу за счет трения о
внутреннюю поверхность трубопровода, может быть
определена соотношением
3
8G fв
(39);
qТР
2 2
2 5
1,82 lg Re d1 1,64 fв d1
• Уравнение (33) преобразуется к линейному,
неоднородному дифференциальному уравнению первого
порядка относительно температуры топлива
dT fв
kL
kL
qТР
T fв
Tну(Т )
(40);
dx G fвc fв
G fвc fв
G fвc fв
• граничным условием, для уравнения (40) при x=0 является
равенство
Tfв(0) = Т0,
(41)
• где Т0 – температура топлива в емкости-хранилище.
92.
• Решением уравнения (40) с учетом граничного условия (41)является функция
qТР
qТР
e
T fв Tну(Т )
T0 Tну(Т )
kL
kL
kL x
G fв c fв
(42);
• которая описывает изменение температуры топлива при
движении его по трубопроводу от емкости-хранилища до
топливного бака ракеты-носителя и позволяет определить
необходимую температуру топлива в емкости-хранилище
по температуре топлива на входе в топливный бак T fв (L)
qТР
T0 Tну(Т )
kL
qТР
T fв ( L) Tну (Т )
kL
e
kL L
G fв c fв
(43);
93. ТЕПЛОПЕРЕДАЧА В КОНСТРУКЦИЯХ ЕМКОСТЕЙ ЗАПРАВОЧНЫХ СИСТЕМ
94.
• В процессе предстартовой подготовки ракет-носителей, двигателикоторых работают на криогенных компонентах топлива, заправка и
подпитка баков ракеты, а также термостатирование в них криогенных
жидкостей осуществляется при подаче компонентов из емкостейхранилищ заправочных систем, имеющих экранно-вакуумную
изоляцию.
• Стенка емкости имеет внутреннюю и внешнюю обечайки, пространство
между которыми заполнено коаксиальными экранами и
I - увеличено
отвакуумировано вакуум-насосной системой.
r3
3
rэi
I
1
Vв,Тн
T0
r4
r1
r2
7
6
2
II
5
4
1- емкость-хранилище криогенного топлива; 2- трубопровод с экранно-вакуумной изоляцией;
3 – топливный бак; 4 – внутренняя обечайка; 5 – экраны; 6–внешняя обечайка; 7 – вакуумная
прослойка.
95.
• Емкости-хранилища заправочных систем могут иметьцилиндрическую, либо сферическую форму
rс
rц
L
• Сферические емкости обладают меньшей поверхностью при
одинаковом объеме по сравнению с цилиндрическими и поэтому им
отдается предпочтение, особенно при создании хранилищ криогенных
компонентов топлива и сжиженных газов (жидкого кислорода, жидкого
водорода, жидкого азота и др.)
• Тепловой поток, поступающий к жидкой среде, расположенной в
емкости определяется суммой теплового потока через боковую
поверхность емкости Qr и ее опорные конструкции Qо
Q Qr nQ 0
(1),
где n - количество опор
96. Определение теплового потока, поступающего через боковую поверхность сферической емкости
• Тепловой поток на наружной поверхности емкостиQrн н 4 r Tну( e ) T4 ;
2
4
(2), Qrн
r3 r4
где
H KH л ,(3)
Tну(е)=Tн+ A4qc/ н (4)
rэi
T0
7
А4- поглощательная способность наружной
6
поверхности емкости; qс - плотность потока
5
4
солнечного излучения
– Т4 – температура наружной поверхности емкости, а для
определения коэффициентов теплоотдачи кн и л используются
зависимости, в которых в качестве характерного размера
используется наружный диаметр емкости d4, а значение числа
Прандтля Prн определяется в соответствии с температурой Тн:
кн = Nu н / d4 , (5)
Re = Vв d4 / н, (6)
Nu = 2+ 0,03 Re0,5 Prн0,33 + 0,35 Re 0,58 Prн0,36 , (7)
r1
r2
97.
• Коэффициент теплоотдачи за счет излучения на наружнойповерхности емкости
Tокр 4 T 4
4
4 c 0
100 100
л
Tн T4
(8)
– где 4 - степень черноты наружной поверхности трубопровода, Токр температура окружения, определяемая как средняя температура
между температурой наружного воздуха и температурой излучения
атмосферы
Токр = 0,5 (Тн + Тиа) , (9)
где tн – температура наружного воздуха, С.
Тиа = 1,36 tн + 239, /К/ (10)
98.
• Тепловой поток, передаваемый теплопроводностью через стенкувнешней обечайки, определяется соотношением
r3 r4
T4 T3
Q r2 4 2
r4 r3
(11)
– где Т3 – температура на внутренней поверхности внешней обечайки; 2 –
коэффициент теплопроводности внешней обечайки; r3 и r4 – внутренний и
внешний радиусы внешней обечайки.
• Тепловой поток, передаваемый излучением между внешней и
внутренней обечайками через систему экранов, определяется
соотношениями для теплообмена излучением между телом и его
оболочкой при наличии между ними экранов:
где
2 , 3э
Q rэ 2,3Э
4
4
T2
2 T3
c 0 4 r2
, (12)
100 100
1
n
1
r22 2
2 1
2,3 i 1 rэi эi
(13) 2,3
1
(14)
2
1 r2 1
2 1
2 r3 3
99.
• Используя коэффициент теплоотдачи излучением между внешней ивнутренней обечайкой через систему экранов ( лэ) соотношение для Qrэ
может быть представлено в виде
Q rэ лэ 4 r T3 T2
2
2
лэ
Т 3 4 Т 2 4
2,3э с 0
100
100
Т3 Т2
(15)
(16)
В формулах (12-16) r2 – наружный радиус внутренней обечайки; лэ –
коэффициент теплоотдачи излучением между внешней и внутренней обечайкой
через систему экранов; Т2 – температура наружной поверхности внутренней
обечайки;ε23э - приведенная степень черноты системы с учетом наличия
экранов; ε23 - приведенная степень черноты системы без экранов; rэi, эi –
радиус и степень черноты i-ого экрана; n – количество экранов в системе; 2, 3
– степени черноты наружной поверхности внутренней обечайки и внутренней
поверхности наружной обечайки соответственно.
100.
• Тепловой поток, передаваемый теплопроводностью черезстенку внутренней обечайки, определяется соотношением
r2 r1
T2 T1 ,(17)
Qr1 4 1
r2 r1
– где Т1 – температура на внутренней поверхности внутренней
обечайки; 1 – коэффициент теплопроводности внутренней
обечайки; r1 – внутренний радиус внутренней обечайки.
• Тепловой поток, передаваемый конвекцией топливу от
внутренней стенки, определяется зависимостью
QrB KB 4 r T1 T0
2
1
(18)
– где Т0 – температура топлива внутри трубы; кв – коэффициент
теплоотдачи конвекцией к топливу от внутренней стенки емкости
101.
• значения кв определяются зависимостями:кв
Nu d1 fв
(19) Ra d
1
d1
При
6•105<
при
108<
Ra <
Ra <
при Ra > 1010
108
1010
g fв d13 T1 T0
Grd1 Prfв
(20)
fв a fв
Nu d1 0,43Rа 0d1,3
Nu d1 0,1Ra 0d1,35
Nu d1 0,01Ra
(21)
0, 4
d1
• где - Nu d , Rа d
числа Нуссельта и Рэлея, при
1
1
определении которых за характерный размер принимается
диаметр внутренней стенки d1; λfв, fв ,аfв , βfв –
теплопроводность, кинематическая вязкость,
температуропроводность и температурный коэффициент
объемного расширения топлива; g – ускорение свободного
падения
102.
• При установившемся теплообмене емкости с окружающей средойсправедливо равенство тепловых потоков
Qrн = Qr2 = Qrэ = Qr1 = Qrв = Qr,
(22)
– где Qr – результирующий тепловой поток, подводимый к топливу через
стенку емкости из окружающей среды.
• Сложение уравнений (2), (11), (15), (17) и (18) с учетом равенств (22)
позволяет получить зависимости для расчета результирующего
теплового потока, подводимого к топливу через стенку сферической
емкости с экранно-вакуумной изоляцией, и температур на поверхностях
внутренней и внешней обечаек емкости
1
r4 r3
1
r2 r1
1
4 THY( e ) T0
Qr
2
2
2
H r4 2 r3r4 лэr2 1r2 r1 KBr1
Qr = кr (Тну(е) Т0),
(23)
– где кr – коэффициент теплопередачи стенки сферической емкости с
экранно-вакуумной изоляцией
4
Kr
r4 r3
1
1
r2 r1
1
2
2
H r4 2 r3r4 лэ r2 1r2 r1 KBr12
(24)
103.
• Температуры на поверхностях внутренней и наружнойобечаек сферической емкости
Qr
T1 T0
KB 4 r12
T4 THY e
Q r r2 r1
T2 T1
4 1r2 r1
(25)
Qr
H 4 r42
(27)
Q r r4 r3
T3 T4
4 2 r4 r3
(26)
(28)
• Поскольку тепловой поток Qr зависит от температур T1 T4,
а они в свою очередь определяются Qr, расчет их значений
проводится методом последовательных приближений.
104.
Алгоритм
расчета
результирующего
теплового
потока, поступающего через стенку сферической
емкости
с
экранно-вакуумной
изоляцией
из
окружающей
среды,
предполагает
следующую
последовательность действий:
–
–
1. Для заданного значения температуры наружного воздуха по
табличным данным определяются значения коэффициентов
кинематической вязкости ( н), теплопроводности ( н) и числа
Прандтля (Prн) для наружного воздуха;
2. С использованием зависимостей (6), (7) и (5), определяется
коэффициент теплоотдачи конвекцией на наружной поверхности
емкости ( кн)
Re = Vв d4 / н,
Nu = 2+ 0,03 Re0,5 Prн0,33 + 0,35 Re 0,58 Prн0,36 ,
кн = Nu н / d4 , (5)
105.
–3.Для первого приближения, поскольку неизвестно значение
температуры наружной поверхности емкости, задается значение
коэффициента теплоотдачи за счет излучения ( л) на наружной
поверхности емкости, пологая, например,
• л = кн;
–
2,3
4.Определяется первое приближение для коэффициента
теплоотдачи излучением между внешней и внутренней
обечайками через систему экранов ( лэ) с использованием
соотношений (14), (13) и (16) и, в предположении, что Т3=Тн,,
Т2=Т0;
1
2 , 3Э
n
1
r22 2
2 1
2,3 i 1 rэi эi
Т 3 4 Т 2 4
2,3э с 0
100
100
Т3 Т2
1
1 r22 1
2 1
2 r3 3
лэ
106.
–5.С использованием зависимостей (20), (21), (19) определяется
коэффициент теплоотдачи конвекцией к топливу от внутренней
обечайки емкости ( кв)
g fв d T1 T0
Ra d1
fв a fв
Для первого приближения можно принять
Т1-Т0=1
3
1
При
6•105<
Ra <
108
при 108< Ra < 1010
при Ra > 1010
кв
–
Nu d1 fв
Nu d1 0,43Rа
Nu d1 0,1Ra
Nu d1 0,01Ra
d1
6. С использованием зависимостей (3) и (4) определяются
значения результирующего коэффициента теплоотдачи н и
условной температуры наружного воздуха Tну(т) для наружной
поверхности трубопровода;
н= кн+ л,
Tну(е)=Tн+ A4qc/ н
0, 3
d1
0,35
d1
0, 4
d1
107.
–7.По зависимостям (24) и (23) находятся коэффициент
теплопередачи стенки сферической емкости (кr) и
результирующего теплового потока, поступающего из
окружающей среды (Qr);
4
Kr
r4 r3
1
1
r2 r1
1
H r42 2 r3r4 лэ r22 1r2 r1 KBr12
Qr = кr (Тну(е) Т0),
–
8.Определяются значения температур на поверхностях
трубопровода (T4, Т3, Т1и T2) с использованием зависимостей (25 28);
Qr
T1 T0
KB 4 r12
T4 THY e
Qr
2
H 4 r4
Q r r2 r1
T2 T1
4 1r2 r1
Q r r4 r3
T3 T4
4 2 r4 r3
108.
––
–
–
9.По значению температуры T4 определяется следующее
приближение для коэффициента теплоотдачи л с
использованием зависимости (8).
10.По значениям температур Т3 и Т2 уточняется коэффициент
теплоотдачи излучением между внешней и внутренней
обечайками через систему экранов ( лэ) с использованием
соотношения (16);
11.Повторяются действия по п.6,7 и 8 и находятся новые значения
температур на поверхностях трубопровода T4н, T3н, T1н и T2н;
12.Сравниваются полученные значения температур с
предыдущими значениями. Если выполняется хотя бы одно из
следующих неравенств:
н
T4 T4 0,1
н
T3 T3 0,1
н
T2 T2 0,1
н
T1 T1 0,1
Повторяются действия по п.9, 10, 11 и 12 до тех пор пока
последующие и предыдущие значения не будут отличаться на
0,1 К
109.
• Расчет может быть осуществлен с помощью ППП Excel,основанный на задании значений температур на
поверхностях внутренней и внешней труб Т1,Т2,Т3 и Т4 по
следующему алгоритму:
– Задание исходных данных:
• 1.Параметры емкости (r1,r2,r3,r4,rЭi,λ1,λ2,εi)
• 2.Параметры топлива в емкости (Т0,λfв, fв,сfв,ρfв,βfв)
• 3.Параметры окружающей среды (Vв,qс,Тн, н, н, λн,
Prн,Dн, ρн,dнн,rф)
– 4.Задание неизвестных параметров Т1,T2,Т3,T4
– 5.Расчет теплопередачи через стенку емкости
(Re,Prн,Nu, кн, л, лэ,аfв, кв, ∑н,ТНу(е),кr,Qr,
Т1н,T2н,Т3н,T4н
110. Определение теплового потока, поступающего через опору емкости
• Для определения зависимостей, определяющих тепловойпоток к топливу через опоры емкости используется
уравнение теплового баланса для элементарного участка
длины опоры dx:
Q x Q Q x dx 0
II - увеличено
,(29)
I
Vв,Тн
Lo
Qx+dx
Qб
Qx
II
dх
х
Qx, Qx+dx - тепловые потоки за счет теплопроводности опоры;
Qб - тепловой поток, подводимый к поверхности опоры из окружающей
среды
111.
• величина теплового потока, подводимого к боковойповерхности опоры на участке dx определяется
следующими зависимостями:
Q H( o ) П THY o T dx (30);
H( o ) KH( o ) л( o ) ф( o ) (31);
Tну(о)=Tн+ Aоqc/ н(о) (32)
• где H( o ) , KH( o ) , л( o ) , ф( o –
соответственно суммарный
)
коэффициент теплоотдачи, коэффициенты теплоотдачи
конвекцией, излучением и за счет фазового перехода на
боковой поверхности опоры; П - наружный периметр
поперечного сечения опоры; Тну(о) - условная температура
наружного воздуха для опоры, учитывающая воздействие
на нее солнечной радиации с плотностью потока qc ; Ао поглощательная способность боковой поверхности опоры;
Т – температура опоры
112.
• Тепловой поток, подводимый к выделенному элементутеплопроводностью, может быть определен соотношением
dT
Q x 0
S ПСО (33);
dx
– где λо – коэффициент теплопроводности опоры; Sпсо – площадь
поперечного сечения опоры
• Тепловой поток, отводимый от выделенного элемента
теплопроводностью, может быть определен соотношением
Q x dx
Q x
dT
d 2T
Qx
dx 0
S ПСО 0 2 S ПСО dx
x
dx
dx
(34);
• Подстановка соотношений (30), (33) и (34) в уравнение (29)
приводит его к виду
2
d T
0
S ПСО H П THY T 0 (35);
dx
2
(о)
0
113.
• Уравнение (35), приведенное к каноническому видуH( о ) П
d 2 T H( о ) П
T
THY 0 (36);
2
0 S ПСО
0 S ПСО
dx
является неоднородным дифференциальным уравнением
второго порядка, характеристическое уравнение которого
и его решение имеют вид
r 2 B 0, где B
r1, 2 B ;
T С1 e x
B
H(о ) П
о S псо
C2e x
B
THY 0
Произвольные постоянные С1 и С2 – определяются из граничных условий:
при x 0
T TH ,
TH c1 c 2 THY 0
BL
BL
T
c
e
c
e
THY 0
0
1
2
при x L
c1
T0 TH e L
T T0
B
THY 0 e L
e
e
c 2 TH c1 THY 0
L B
L B
B
;
114.
• С использованием уравнения длятемпературы опоры находится тепловой
поток, подводимый к топливу по ее
конструкции
dT
Q 0 о SПС0
dx x L
dT
L
c1 Be
dx x L
Qo o c1 Be
L B
B
c 2 Be
c 2 Be
L B
L B
S
псо
115.
• Потери криогенного топлива за счетиспарения Gисп под воздействием
суммарного теплового потока, поступающего
в емкость определяются из уравнения
Q Q r nQ 0 G исп rfф
G исп
Q r nQ 0
rfф
где rfф – удельная теплота испарения криогенного топлива
116. Температурная подготовка КРТ на стартовых и технических комплексах космодромов и ракетных базах
117. Задачи температурной подготовки КРТ
На стартовых комплексах ракет космического назначения (РКН),двигательные установки которых используют углеводородные горючее (УВГ)
марок РГ-1 и Т1, оборудованием заправочных систем должна проводиться
температурная подготовка УВГ перед заправкой в топливные баки РКН.
Температура горючего Т1 должна составлять минус 2-5 °С, а РГ-1 –
минус 25-30 °С, которые достигаются за счет проведения охлаждения (нагрева)
УВГ в емкостях-хранилищах стартового комплекса. При снижении температуры
КРТ достигается увеличение его плотности, что позволяет разместить в
топливных баках ракеты большие по массе количества ракетного топлива.
На технических комплексах и заправочных станциях космических
аппаратов и разгонных блоков космодромов, а также на ракетных базах хранения
ракетного топлива и стартовых комплексах РКН, двигательные установки
которых используют компоненты НДМГ-АТ, также должна проводиться
температурная подготовка КРТ перед заправкой в топливные баки КА, РБ, РКН и
боевых ракет.
Процессы температурной подготовки КРТ являются одними из
наиболее энергоемких и длительных процессов, требующих определения
рациональных технологий и режимов охлаждения (нагрева) ракетного топлива
оборудованием стартовых и технических комплексов космодромов .
118.
Охлаждение КРТ с использованиемжидкого азота методом криогенного
барботажа
119. Охлаждение УВГ может осуществляться при непосредственной подаче жидкого азота в емкость-хранилище через барботажный аппарат с
последующим рассыщением горючего сцелью удаления из него растворенного азота.
4
2
9
1
3
5
8
7
6
Технологическая схема системы заправки РКН с возможностью предварительной температурной подготовки
УВГ на стартовом комплексе.
1 – емкость-хранилище УВГ; 2 – емкость-хранилище жидкого азота; 3 – хранилище газообразного азота
высокого давления; 4 – газовый редуктор; 5 – насосная станция; 6 – теплообменник-нагреватель; 7 – запорная
арматура; 8 – фильтр; 9 – топливный бак РКН
120. Физическая картина взаимодействия жидкого азота с жидкими средами
121. Физическая картина взаимодействия жидкого азота с жидкими средами
122.
42
1
3
5
8
7
6
9
Охлаждение топлива перед
заправкой в топливные баки РКН
осуществляется
посредством
барботажа УВГ жидким азотом,
который вследствие теплообмена с
топливом переходит в газообразное
состояние и при движении к
поверхности жидкости в емкостихранилище
нагревается
до
ее
текущей температуры.
Из наджидкостного пространства газообразный азот отводится в дренажную
магистраль заправочной системы. После охлаждения УВГ до требуемой
температуры проводится операция рассыщения топлива с целью удаления из
него растворенного азота, что достигается при повышении давления в емкости за
счет подачи в нее газобразного азота при закрытом дренажном клапане с
последующим резким сбросом давления при его открытии.
При необходимости нагрев УВГ в емкости осуществляется при работе
насосной станции, обеспечивающей циркуляцию топлива через теплообменникнагреватель с возвратом УВГ в емкость-хранилище.
123.
124.
125.
12
126.
127.
Системы охлаждения углеводородного горючего при криогенном барботаже
по относительным затратам жидкого азота и времени операции охлаждения
являются наиболее эффективными.
При криогенном барботаже происходит унос наиболее легких и «ценных» в
энергетическом отношении фракций УВГ;
Азот непосредственным образом контактирует с КРТ и по завершению
операции охлаждения оказывается газонасыщенным, что в свою очередь
приводит к необходимости проводить операцию рассыщения, являющейся
причиной дополнительных затрат азота, а также временных и энергетическим
затрат.
В виду низкой температуры кипения жидкого азота не представляется
возможным использовать данный способ для охлаждения топлив с высокой
температурой замерзания.
Возможность осуществления охлаждения КРТ при подаче жидкого азота в
массу топлива применима только к экологически чистым КРТ
(углеводородным ракетным горючим), имеющим низкую температуру
замерзания.
Перечисленные обстоятельства свидетельствуют о необходимости
применения для охлаждения и нагрева КРТ теплообменников.
128. Температурная подготовка КРТ с использованием теплообменников и жидкого азота
129. Схема охлаждения горючего с использованием теплообменника и жидкого азота на СК «Союз»
Тв130. Системы охлаждения КРТ с применением жидкого азота и промежуточного теплоносителя.
Схема двухконтурной системы охлаждения окислителя РН «Рокот» настартовом комплексе космодрома «Плесецк».
131. Уравнение процесса охлаждения горючего с использованием теплообменника и жидкого азота
Тв132. Решение уравнения процесса охлаждения горючего с использованием теплообменника и жидкого азота
133. Теплоотдача при кипении жидкости на теплообменной поверхности
При кипении жидкости на теплообменной поверхности существуют следующиережимы кипения: пузырьковый (1), переходный (2) и пленочный (3).
ΔТ
1
2
3
134. Определение размеров секции теплообменника
135. Зона кипения при движении жидкости вдоль теплообменной поверхности
136. Зона нагрева газообразного азота при движении вдоль теплообменной поверхности
137. Схема размещения системы охлаждения на СК «Союз»
138. Технические характеристики системы охлаждения керосина (нафтила) жидким азотом с применением секций теплообменников на
стартовом комплексе ракеты «Союз-СТ»Количество резервуаров жидкого азота
Вместимость резервуара жидкого азота, м3
Масса жидкого азота в резервуаре, кг, не более
1
112
85760
Количество охлаждаемого керосина, кг:
– в железнодорожном заправщике
85000
– в автомобильном заправщике
10500
Минимальная температура охлаждения горючего, °С:
– в железнодорожном заправщике
минус 3±2
– в автомобильном заправщике
минус 34
Расход горючего через каждый охладитель, м3/ч
30
Максимальное время охлаждения горючего, ч
– в железнодорожном заправщике:
– при работе двух насосов
10
– при работе одного насоса
20
– в автомобильном заправщике при работе одного насоса
4
139. Проблемные вопросы при реализации охлаждения КРТ в теплообменнике при тепловом взаимодействии с жидким азотом
• Ввиду низкой температуры кипения жидкого азота в теплообменнике(~80 К) возможно намерзание КРТ на охлажденной поверхности
теплообменника;
• Секции теплообменника типа «труба в трубе» имеют значительные
размеры, оборудование системы охлаждения размещается
стационарно на открытой площадке и занимает площадь более 100
кв.м;
• Из-за недорекуперации по температуре газообразного азота,
выходящего из теплообменника, существенной массы и теплоемкости
теплообменника, теплопритоков к поверхности теплообменника
затраты азота на охлаждение КРТ в 2 раза превышают аналогичные
характеристики систем охлаждения, работа которых основана на
криогенном барботаже КРТ жидким азотом;
140. Охлаждение КРТ с применением жидкого азота и промежуточного теплоносителя
Схема двухконтурной системы охлаждения КРТ сприменением жидкого азота и промежуточного
теплоносителя.
1 – емкость с горючим, 2 – насос горючего, 3 –
теплообменник, 4 – емкость с теплоносителем, 5 – насос
теплоносителя, 6 – емкость с жидким азотом, 7 – регулятор
расхода, 8 – газификатор, 9 – дроссельная шайба.
Схема с применением промежуточного
теплоносителя применяется в случаях, когда
разность между начальной и потребной
конечной температурой КРТ невелика или в
случае, если компонент имеет сравнительно
высокую
температуру
замерзания.
Применение схем без промежуточного
теплоносителя в этом случае связано с риском
намерзания твёрдой фазы КРТ на элементах
системы охлаждения (стенках теплообменника
или барботёра). Такими свойствами обладают,
к примеру, некоторые высококипящие КРТ,
относящиеся к азотным окислителям и
имеющие диапазон температур существования
в жидком виде -10…+20 ˚С. Двухконтурная
система
охлаждения
с
помощью
промежуточного теплоносителя состоит из
двух рабочих емкостей (для охлаждаемого
КРТ и теплоносителя), двух контуров с
теплообменником и системы охлаждения
теплоносителя.
141. Математическая модель теплообмена в двухконтурной системе охлаждения КРТ
142. Математическая модель теплообмена в двухконтурной системе охлаждения КРТ
143. Математическая модель теплообмена в двухконтурной системе охлаждения КРТ
Схема тепловых потоков, действующихна продукт в контуре охлаждения
144. Математическая модель теплообмена в двухконтурной системе охлаждения КРТ
145. Структурная схема вычислений теплообмена в двухконтурной системе охлаждения КРТ
Исходныеданные
Расчёт
тепловыделения
насосных
установок
Параметрический
расчёт
коэффициентов
теплопередачи для
теплообменника
Параметрический
расчёт
коэффициентов
теплопередачи для
магистралей
Параметрический
расчёт изменения
температур
жидкостей в
теплообменнике
Параметрический
расчёт изменения
температур
жидкостей в
магистралях
Параметрический расчёт изменения
температур жидкостей при циркуляции по
контурам
Расчёт процесса охлаждения
Результаты расчёта
Параметрический
расчёт
коэффициентов
теплопередачи
для емкостей
146. Проблемные вопросы при реализации охлаждения КРТ в теплообменнике с применением жидкого азота и промежуточного теплоносителя в
двухконтурной системе охлажденияПри одновременной подаче жидкого азота в емкость с теплоносителем и
работе насоса, осуществляющего циркуляцию теплоносителя через
теплообменник, необходимо исключать попадание паров азота во входной
патрубок насоса для исключения динамических нагрузок на рабочее колесо
насоса;
При применении последовательной технологии «охлаждение теплоносителя охлаждение КРТ» динамические нагрузки на насос теплоносителя
исключаются, но при этом требуется захолаживать значительные объемы
теплоносителя, что требует увеличения затрат жидкого азота на выполнение
операции охлаждения;
Наличие двух насосных установок также является недостатком двухконтурной
системы охлаждения, в виду бо́льшей стоимости системы, ее меньшей
надежности, а также необходимости дополнительного расхода жидкого азота
на компенсацию теплоты от работающих насосов.
147. Перспективные технологии охлаждения КРТ с применением жидкого азота
Размещение теплообменника системы охлаждения КРТ в резервуаре с теплоносителем
(антифризом) позволяет исключить один насос и контур циркуляции антифриза через
теплообменник
Схема системы охлаждения КРТ жидким азотом с теплообменником, размещенным в
резервуаре с антифризом.
1 – емкость-хранилище КРТ; 2 – топливный бак РКН; 3 – теплообменник; 4 − резервуар с
антифризом; 5 − насос; 6 – резервуар с жидким азотом; 7 – хранилище газообразного
азота высокого давления; 8− газовый редуктор; 9−дренажный клапан; 10 – нагреватель.
148.
Система позволяет реализовать последовательно сначала охлаждение антифриза
жидким азотом до температуры, при которой будет обеспечиваться охлаждение топлива
без его намерзания на внутренних поверхностях теплообменника, а затем при
включении насоса 5 − охлаждение топлива в резервуаре КРТ с поддержанием
температуры антифриза за счет подачи жидкого азота.
Помимо последовательного режима охлаждения система может обеспечить и
одновременное охлаждение антифриза и КРТ. При этом обеспечивается возможность
подготавливать большие дозы ракетного топлива, полностью используя как скрытую
теплоту фазового перехода азота, так и изменение температуры его газообразной фазы,
исключая недорекуперацию и повышая эффективность системы по затратам жидкого
азота на операцию охлаждения.
149. Математическая модель теплообмена в системе при размещении теплообменника системы охлаждения КРТ в резервуаре с теплоносителем
(антифризом)150. Математическая модель теплообмена в системе при размещении теплообменника системы охлаждения КРТ в резервуаре с теплоносителем
(антифризом)151. Математическая модель теплообмена в системе при размещении теплообменника системы охлаждения КРТ в резервуаре с теплоносителем
(антифризом)152. Математическая модель теплообмена в системе при размещении теплообменника системы охлаждения КРТ в резервуаре с теплоносителем
(антифризом)153.
Пример изменения температуры горючего РГ-1 в емкости заправочной системы и
антифриза А-65 в резервуаре с расположенным в нем теплообменником при подаче
жидкого азота через барботер в массу антифриза
1 – температура антифриза;
2 – температура РГ-1
2
1
ч
изменение массового расхода и затрат жидкого азота в системе в процессе выполнения
операции охлаждения
1 – массовый расход ЖА кг/ч;
2 – затраты (кг) ЖА на
охлаждение РГ-1
154. Охлаждениe КРТ с использованием жидкого азота и теплообменника, размещенного непосредственно в емкости с КРТ
Применение технологий охлаждения КРТ с использованием жидкого азота итеплообменников, размещаемых непосредственно в емкостях с КРТ, не требует
применения насосов и позволяет осуществлять режимы охлаждения топлива с
большей эффективностью.
1 – емкость-хранилище
ракетного топлива; 2 –
емкость-хранилище жидкого
азота; 3 – теплообменник
охлаждения и нагрева
ракетного топлива; 4 –
хранилище газообразного
азота высокого давления; 5 –
газовый редуктор; 6 –
насосная станция; 7 –
запорная арматура; 8 –
воздухонагреватель; 9 –
компрессор; 10 – фильтр; 11
– топливный бак; 12 –
барботер газообразного
азота.
155. Охлаждениe КРТ с использованием жидкого азота и теплообменника, размещенного непосредственно в емкости с КРТ
Охлаждение и нагрев топлива в емкостихранилище (1) перед заправкой втопливные бак летательного аппарата (11)
осуществляется посредством теплообмена
с наружной поверхностью теплообменника
(3). Режим охлаждения топлива
осуществляется подачей жидкого азота из
емкости-хранилища жидкого азота (2) при
поступлении в нее под давлением
газообразного азота из хранилища
газообразного азота высокого давления (4)
через газовый редуктор (5). Жидкий азот
вводится в нижнюю часть теплообменника
(3) и вследствие теплообмена с топливом
переходит в газообразное состояние и
отводится в дренажную магистраль
системы заправки наземного комплекса.
Для периодического перемешивания и выравнивания температуры топлива в емкости может использоваться
насосная станция заправочной системы (6). Для достижения той же цели может использоваться барботаж
емкости сухим газообразным азотом через барботер 12.
Режим нагрева топлива в емкости (1) осуществляется подачей в теплообменник воздуха, нагреваемого в
воздухонагревателе 8, при работе компрессора 9. При движении воздуха через барботер, размещенный в
теплообменнике, заполненном антифризом, происходит интенсивный теплообмен между воздушными пузырями
и антифризом, обеспечивая нагрев поверхностей теплообменника и топлива в емкости заправочной системы.
156. Охлаждениe КРТ с использованием жидкого азота и теплообменника, размещенного непосредственно в емкости с КРТ
157. Нагрев КРТ с использованием теплообменника, размещенного непосредственно в емкости с КРТ
158. Изменение температуры РГ-1 в емкости заправочной системы РКН «Союз» при выполнении операции охлаждения с использованием жидкого
азота и теплообменника с антифризомА-65, расположенного во внутреннем пространстве емкости
T, °C
τ, ч
температура топлива РГ-1;
температура антифриза А-65
159.
Относительные затраты жидкого азота на охлаждение РГ-1 с использованиемтеплообменника, размещенного непосредственно в емкости с КРТ, в зависимости от
требуемого уровня его охлаждения
160. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ МЕЖДУ ПОВЕРХНОСТЯМИ КОНСТРУКЦИЙ, ПРОИЗВОЛЬНО ОРИЕНТИРОВАННЫМИ В ПРОСТРАНСТВЕ
161.
• При произвольной ориентации поверхностей конструкцийF1,T1, 1,A1
Q2
Результирующий тепловой поток,
передаваемый от первой ко второй
поверхности
Q12 Q1 Q 2
Q1
F2,T2, 2,A2
Е эф1
__
Q1 Е эф1F1 12 ; 2
Е1
1
; 4
q 12 1
А1
А1
Е эф 2
(1)
__
Q 2 Е эф 2 F2 21 ; 3
Е2
1
; 5
q 21 1
А2
А2
__
__
Е1 __
1 E 2 __
1
; 6
Q12
F1 12 q12 F1 12 1
F2 21 q 21F2 21 1
А1
А1 A 2
A2
162.
q12 F1 Q12 ; 7 q 21F2 Q 21 Q12 ; 8Q12
E1 __
E 2 __
F1 12
F2 21
A1
A2
; 9
__
__ 1
1
1 12
1 21
1
A1
A2
4
T1
E1 c0 1
; 10
100
4
T2
E 2 c0 2
; 11
100
163.
1 A1; 12 2 A2 ; 13• По закону Кирхгофа
4
Q12
4
T1
T2
c 0 F1 12
c 0 F2 21
100
100
; 14
__
__ 1
1
1 12
1 21
1
A1
A2
__
При
__
T1 T2 ; Q12 0;
__
__
F1 12 F2 21 ; 15
свойство “взаимности”
(Площади взаимного облучения равны между собой)
164.
• Окончательное соотношение для результирующеготеплового потока между произвольно ориентированными
поверхностями
4
Q12
__
4
T1 T2
__
100 100
c 0 F1 12
; 16
__
__ 1
1
1 12
1 21
1
A1
A2
__
При 12 21 1
(случай теплообмена между плоскими поверхностями)
__
При
__
12 1; 21
F1
;
F2
(случай теплообмена между выпуклым телом и его
оболочкой)
165. Определение средних угловых коэффициентов облучения в замкнутой системе поверхностей теплообмена
• Тепловой поток излучения от поверхности 1__
F2
F3
__
Q1 Q1 12 Q1 13 ; (1)
n __
__
12 13 1; (3)
__
12 F1 13 F1 F1; (6)
__
1 12 13; 2
- свойство замкнутости системы (в замкнутой
системе сумма угловых коэффициентов для
каждой поверхности равна 1). Применительно к
__
__
__ данной
__ системе из 3-х поверхностей:
i 1
__
__
1i 1
F1
__
__
__
12 F1 21 F2 ; (9)
__
21 23 1; (4)
__
__
31 32 1; (5)
__
21 F2 23 F2 F2 ; (7) 31 F3 32 F3 F3 ; (8)
по свойству взаимности
__
__
23 F2 32 F3 ; (10)
__
__
13 F 31 F3 ; (11)
166.
• при попарном сложении уравнений (6), (7) и (9)F1 F2 F3
12
; 12
2F1
F2 F1 F3
21
; 13
2F2
__
__
F3 F1 F2
31
; 15
2F3
__
F1 F3 F2
13
; 14
2F1
__
F2 F3 F1
23
; 16
2F2
__
F3 F2 F1
32
; 17
2F3
__
Обобщенная формула определения
средних угловых коэффициентов
облучения
__
ij
Fi Fj Fk
2Fi
167. Примеры определения тепловых потоков и средних угловых коэффициентов
• Две взаимно перпендикулярные поверхностиУсловия: L h;
Т1>T2
L
Тепловой поток,
передаваемый излучением
от первой поверхности ко
второй
L a;
2
4
h
T1 T2
100
100
__
1
Q12 c 0 aL 12
1
__ 1
1 12
1 21
A1
A2
__
a
aL hL L h 2 a 2 1 1 h 1 h 2
12
1;
2
2aL
2 2a 2 a
__
hL aL L h 2 a 2 1 1 a 1
a2
21
1 2 ;
2hL
2 2h 2
h
__
4
168.
• Две параллельные плоскостиУсловия: L h;
Т1>T2
L
2
C
4
T1 T2
100 100
D
__
h
Q12 c 0 aL 12
1
A
4
1
__ 1
1 12
1 21
A1 __ A 2
__
__
B
a
L a;
замкнутости
__ по свойству
__
__
1AC 12 1BD 1;
__
12 1 1AC 1BD ;
aL hL L h 2 a 2 1 1 h 1 h 2
1AC
1;
2
2aL
2 2 __
a 2 a
__
__
из условий симметрии
__
__
12 1 2 1AC
1BD 1AC ;
2
h
h
1 1
1
2
a
a
169. Теплообмен излучением в замкнутой системе, состоящей из n поверхностей
• Результирующий тепловой поток излучения для i-той поверхностиQрезi q резi Fi ; 1 q резi Eэфi Eпадi ; 2
Тk, Fk, k, Rk
n
Eэфi
Eпадi
E пад i
E
k 1
эф k
n
ki Fk
Fi
Тi, Fi, i, Ri
n __
__
E эф i E эф i ik E эф i ik ; 4
k 1
k 1
n
__
E
k 1
__
эф k
ik Fi
Fi
n
__
E эф k ik ; 3
k 1
n
__
q резi E эф i E эф k ik ; 5
k 1
n
__
E эф i E i R i E пад i E i R i E эф k ik ; 6
k 1
4
Ti
E i c0 i
; 7
100
170.
• Из системы n-уравнений вида4
Ti
E эф i R i E эф k ik c 0 i
; 8
100
k 1
n
__
…………………………………………….
…………………………………………….
находятся
E эф i , E эф k
Для этого предварительно определяются средние
угловые коэффициенты __
ik
171. Приближенная оценка с использованием зависимостей для теплообмена между телом и оболочкой
• Fi является телом, остальные поверхности – оболочка4
4
__
Ti T k
Qрезi q резi Fi п ikc0 Fi
; 9
100 100
E
n
E
1
F Fk Fi ; 11
п ik
; 10
1
k 1
F
1
i
Т, F, , R
1
__
i F
k
4
4
n
n
Tk
Ti
4
__
k Fk i Fi
Fk
Fi
__
100
Tk
k 1 100
i 1
; (13)
k
; 12
100
F
F
Тk, Fk, k, Rk
эфi
падi
i
i
i
i
172. Совместный теплообмен конвекцией и излучением в воздушных прослойках конструкций
• Для горизонтальных прослоек при Т1>T2 конвекция отсутствуетq q12л q12т
приT1 T2
δ
Т1
q12 л
q12 т
Т2
T1 4 T2 4 f
12c0
T1 T2 ;
100 100
f f Tf ; гдеTf 0,5 T1 T2
• Для горизонтальных прослоек при Т1<T2 , для наклонных и
вертикальных прослоек конвекция развивается из-за разности
плотностей
T 4 T 4
q q12 л q12к 12c 0 2 1 к f T2 T1 ;
100 100
коэффициен т
δ
конвекции
q12 л
q12 к
3
g
T
T
0 , 25
2
1
;
к 0,18 Grf Prf ; Grf Prf
f a f
173. Совместный теплообмен конвекцией и излучением при термостатировании объектов ракетно-космической техники
174.
• При выполнении операций транспортировки и предстартовойподготовки требуется поддерживать температурный режим КА и
отсеков РН в определенных пределах. Для этих целей применяются
воздушные СТ, с помощью которых либо под ГО, либо в ТПК подается
подогретый либо охлажденный воздух.
175. Схема теплообмена при термостатировании
Режим обогрева (зимний режим термостатирования) Т m THОТ – объект термостатирования
I - увеличено
ГО – головной обтекатель (оболочка)
q1л
Тн
I
ОТ
q1к Тm
q2к
Т1
Т2
qкн
qлн
Т3
q1к – плотность теплового потока
конвекцией от воздуха к ОТ;
Vв
ГО
qт
Тm
q2к – плотность теплового потока
конвекцией от воздуха к ГО;
qлв – плотность лучистого теплового
потока от ОТ к ГО;
qт – плотность теплового потока за
счет теплопроводности ГО;
qкн – плотность теплового потока
конвекцией к наружному воздуху;
qлн – плотность лучистого теплового
на наружной поверхности ГО;
176.
• Уравнения для определения плотностей тепловых потоковq1K 1K Tm T1
q 1Л
q 2K 2K Tm T2
(1)
T1 4 T2 4
12 с 0
(3)
100 100
q1Л 1Л T1 T2
q1K q1Л
(7)
(5)
12
1Л
1
1 F1 1
1
1 F2 2
(2)
(4)
T1 4 T2 4
12 C 0
100 100
(6)
T1 T2
1K Tm T1 1Л T1 T2
Температура поверхности
объекта термостатирования
1K Tm 1Л T2
T1
1K 1Л
(9)
(8)
177. Определение коэффициентов теплоотдачи в кольцевом зазоре между ОТ и ГО
• при скорости воздуха в зазоре < 1 м/с преобладаетсвободная конвекция
g Tm T1
1K 0,15
(10)
ma m
• при скорости воздуха в зазоре > 1 м/с преобладает
вынужденная конвекция
m3
1K
Nu m
(11)
dэ
Nu 0,021Re
4 d 22 d12
dЭ
d 2 d1 (14)
4 d 2 d1
w ср
4G m
m d 22 d12
(16)
0,8
dЭ
0, 4
m
Pr
Re d Э
(12)
w ср d Э
m
4S
dЭ
(13)
П
(15)
Wср – средняя скорость воздуха в зазоре;
Gm – массовый расход воздуха, подаваемый из
системы термостатирования
178.
• Определение температур на поверхностях ГОq2л
qт
q1к Тm
q2к
Т1
Т2
qкн
qлн
Т3
q 2 К q 2 Л q T q КH q ЛН
q 2K 2K Tm T2
при скорости воздуха в зазоре < 1 м/с
преобладает свободная конвекция
2 К 0,15 m 3
g Tm T2
ma m
(17)
(18)
при скорости воздуха в зазоре > 1 м/с
преобладает вынужденная конвекция
(19)
q 2 Л 2 Л Tm T2 (21) 2 Л
2K 1K
4
(20)
4
T1 T2
12 с 0
100 100 F1
Tm T2
F2
(22)
q В q 2К q 2 Л 2K 2 Л Tm T2 2 Tm T2 (23)
179.
• Плотность теплового потока за счет теплопроводности ГО1
T2 T3 (24)
qT n
i
i 1 i
• Плотность суммарного теплового потока на наружной
поверхности ГО
q H q КH q ЛH KH T3 TH ЛН T3 TH Н T3 TH (25)
q B qT q H q
n
1
i
1
q
2 i 1 i H
к ГО
Tm TH (27)
1
n
i
1
1
2 i 1 i H
(29)
(26)
q к ГО Tm TH
(28)
q
T2 Tm
2
(30)
q
T3 TH
H
(31)
Расчет qΣ, Т1, Т2, Т3 проводится методом последовательных приближений
180.
• Определение теплового потока через поверхность ГОF2 F3
Q q Fср q
2
(32)
• Необходимый расход воздуха для термостатирования
Q
GB
C p T
(33)
T Tm Tm Tm Tm 2 Tm
(34)
• Тm ±∆Тm – допустимый диапазон температур под головным
обтекателем
181.
• Отличия теплообмена для режима охлаждения(летнего режима термостатирования)
Схема теплообмена
q1л
q1к Тm
Т1
qт
q2к
Т2
qкн
q к ГО TH УСЛ Tm
qс
qлн
TH УСЛ
Т3
Tm 1K T2 1Л
T1
1K 1Л
q
T2 Tm
2
(37)
Т 3 TH усл
qc A3
TH
H
q
H
(39)
(36)
(38)
(35)
182. Алгоритм вычислений
• 1) Ввод параметров объектатермостатирования
q1
л
q1к Т
m
Т1
qт
q2к
Т2
qкн
qлн
Т3
d1, м
d2, м
d3, м
F1, м2
F2, м
λ1,Вт/(мК)
λ2,Вт/(мК)
ε(1)
ε(2)
ε(3)
δ1 м
δ2, м
183.
• 2)Ввод параметроввоздуха внутри
объекта
термостатирования
Tm, Цельс
∆Tm, Цельс
λm, Вт/(мК)
ν.m, м2/с
Сpm, Дж/(кгК)
ρm, кг/м3
Prm
184.
• 3)Ввод параметровокружающей среды
Vв, м/с
qc, Вт/м2
Tн, Цельс
νн, м2/с
λн
Prн
ρн, кг/м3
185.
• 4)Заданиенеизвестных
параметров
Т1
q1л
qт
q1к Тm
q2к
Т1
Т2
qкн
qлн
Т3
T2
Т3
Gв, кг/с
186.
• 5)Расчеттеплопередачи
через стенку
оболочки объекта
термостатирования
Re(d3)
Pr3
Nu(н)
α кн(т)
Тиа, К
Токр, К
(Токр)/100
(Т3+273)/100
αлн, Вт/(м2К)
ε12
(Т1+273)/100
(Т2+273)/100
α1л, Вт/(м2К)
187.
• 5)Расчеттеплопередачи
через стенку
оболочки объекта
термостатирования
w, м/с
dэ
Redэ
Nudэ
α1к, Вт/(м2К)
Т1
α2к, Вт/(м2К)
α2л, Вт/(м2К)
α2Σ, Вт/(м2К)
αΣн, Вт/(м2К)
Кго
qΣ
Т2н
Т3н
QΣ, Gв
188. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛО- И МАССОПЕРЕНОСА В СПЛОШНЫХ СРЕДАХ
189.
• В покоящейся среде теплоперенос осуществляется посредствомтеплопроводности
z
Вт
q v 3 мощность объемного тепловыделения
м
Q x dx
Qx
dz
dy
dx
y
Q y Q y dy
x
T
Q x
dydz ;
x
Q x
Q x dx Q x
dx ;
x
2T
Q x Q x dx 2 dx dy dz ;
x
По аналогии в направлениях осей у и z
2T
2T
2 dx dy dz ; Qz Qz dz 2 dx dy dz ;
y
z
T
Q x Q x dx Q y Q y dy Q z Q z dz q v dx dy dz c
dx dy dz ;
дифференциальное уравнение
T 2T 2T 2T q v
2 2 2 ; 1 теплопереноса в неподвижной среде
c x
y
z c
(уравнение теплопроводности)
λ-коэффициент теплопроводности;
ρ-плотность; с-удельная теплоемкость
a
c
- коэффициент
температуропроводности;
190. Условия однозначности ( краевые условия ):
Начальное условие при = 0
Граничные условия:
–
А) 1-ого рода
Задание температуры
поверхности
T f1 (x, y, z)
Tx x 0 f 2 y, z, ;
Tx x 0 T1;
T
T
qc ;
f
y
,
z
,
;
– Б) 2-ого рода
3
x x x 0
x x x 0
Задание теплового
потока на поверхности
T
к Tf Tx x 0 ;
– В) 3-его рода
Задание теплообмена на x x x 0
поверхности с жидкостью
–
Г) 4-ого рода
Задание условий на
границе контакта двух
поверхностей
–
Д) 5-ого рода
T
T
1 1
2 2
;
x
x
x x 0
x x 0
T1x x 0 T2 x x 0 ;
T
q к q л q ф Аq c ;
x x x 0
Задание теплового потока при сложном
теплообмене на поверхности
191.
• В движущейся несжимаемой среде помимо теплопроводностиперенос теплоты осуществляется конвекцией
z
Q x
T
Q x dx Q x
dx ;
Qx
cw x T dydz ;
x
x
Вт
q v 3 мощность объемного тепловыделения
м
2T
T
dxdydz ;
Q x Q x dx 2 cw x
x
x
wx
Q x dx
Qx
2T
T
dxdydz ;
Q y Q y dy 2 cw y
dz
y
y
dy
dx
y
x
Q z Q z dz
2T
T
dxdydz ;
2 cw z
z
z
Q x Q x dx Q y Q y dy Q z Q z dz q v dx dy dz c
T
dx dy dz ;
T
T
T
T 2T 2T 2T q v
wx
wy
wz
2 2 2 ; 2
x
y
z c x
y
z c
уравнение теплопереноса (энергии) для
движущейся несжимаемой среды
192.
• Для получения решения уравнения (2) его необходимодополнить уравнениями движения и неразрывности
__
2w x 2w x 2w x
w x
w x
w x
w x
p
X
wx
wy
wz
2
2
2
x
y
z
x
x
y
z
;
__
2w y 2w y 2w y
w y
w y
w y
w y
p
;
Y
wx
wy
wz
2
2
2
x
x
y
z
y
y
z
__
2w z 2w z 2w z
w z
w z
w z
w z
p
;
Z
wx
wy
wz
2
2
2
x
y
z
z
y
z
x
wx wy wz
0 ;
x
y
z
где - w x , w y , w z составляющие скорости движения;
__
__
__
X, Y, Z - массовые силы;
р - давление;
среды.
μ - коэффициент динамической вязкости
193.
• В движущейся несжимаемой среде массоперенос осуществляетсяпосредством диффузии и конвекции
c1 c 2
z
кг
m 1v 3
м с
wx
M 1x
y
x
2c1
c1
dxdydz ;
M1x M1x dx D1 2 w x
x
x
2c1
c1
dxdydz ;
M1y M1y dy D1 2 w y
y
y
dz
dx
c1
M1x D1
c1w x dydz ; M1x dx M1x M1x dx ;
x
x
M1x dx
dy
где c1 и с2 - концентрации компонентов смеси
2c1
c1
dxdydz ;
M1z M1z dz D1 2 w z
z
z
c
M1x M1x dx M1y M1y dy M1z M1z dz m1v dx dy dz 1 dx dy dz ;
2c1 2c1 2c1
c1
c1
c1
c1
wx
wy
wz
D1 2 2 2 m1v ; 3
x
y
z
y
z
x
уравнение массопереноса для движущейся несжимаемой среды.
194. ОСОБЕННОСТИ УРАВНЕНИЙ ТЕПЛОМАССОПЕРЕНОСА ДЛЯ ТУРБУЛЕНТНЫХ ТЕЧЕНИЙ
• Уравнения (2)для ламинарных течений
__ и (3) справедливы
__
'
wx
w x w x w x w x осредненная скорость
__
wx
w 'x
w 'x пульсационная скорость
w 'x
__
wx
масштаб (степень)
турбулентности
За счет турбулентности в движущейся среде повышаются касательные
напряжения, тепло- и массоперенос
__
__
wx
w x
к т
1
y
y
μ,ν - коэффициенты динамической и кинематической вязкости среды;
μт=ρετ коэффициент турбулентной динамической вязкости;
ετ - коэффициент турбулентного переноса количества движения, который
является функцией параметров турбулентного движения и определяется
экспериментальным путем.
195.
• Плотность теплового потока в турбулентной среде__
__
q c
q c T
Т
qт т
1
1
y
y
__
__
T
Pr T
1
y
Prт y
т q c коэффициент турбулентной теплопроводности;
c число Прандля – комплекс теплофизических
Pr
параметров среды
a
турбулентное число Прандтля, которое является функцией
Prт параметров турбулентного движения и определяется
q
экспериментальным путем.
• Плотность потока массы в турбулентной среде
__
__
__
__
Prd c1
D1т c1
D1т c1
c1
m1т D1 D1т
D1 1
D1 1
D1 1
y
y
D1 y
D1 y
Pr
d
т
D1т коэффициент турбулентной диффузии
диффузионное число Прандтля
D1
Prd т турбулентное диффузионное число Прандтля.
D1т
Prd
196.
• уравнение теплопереноса (энергии) для движущейся втурбулентном режиме несжимаемой среды
__
__
__
__
Т
T
T
T
wx
wy
wz
x
y
z
__
__
__
__
__
__
Pr T Pr T Pr T q v
1
1
1
; 4
c x Prт x y Prт y z Prт z c
• уравнение массопереноса для движущейся в турбулентном
режиме несжимаемой среды
__
__
__
__
с1 __ с1 __ с1 __ с1
wx
wy
wz
x
y
z
__
__
__
Pr c
Pr c
Pr c
D1 1 d 1 1 d 1 1 d 1 m1v ; 5
x Prd т x y Prd т y z Prd т z
197. УРАВНЕНИЯ ТЕПЛО- И МАССОПЕРЕНОСА В СПЛОШНЫХ СРЕДАХ В ПРИБЛИЖЕНИЯХ ПОГРАНИЧНОГО СЛОЯ
198.
• Для ламинарного потока в предположении о малости массовых силтечение и тепломассо-перенос в среде при обтекании плоской
поверхности описывается системой уравнений
2wx 2wx
w x
w x
1 p
; 1
Уравнения движения:w x
wy
2
2
x
y
x
W ,
y
x
y
T ,
2w y 2w y
w y
w y
1 p
; 2
C1
wx
wy
2
x 2
x
y
y
y
Уравнение сплошности:
x
0
L
Tw , C1 w
w x w y
0 ; 3
x
y
Уравнения тепло- и массопереноса:
2T 2T
T
T
wx
wy
a 2 2 ; 4
x
y
y
x
2 c1 2 c 1
с1
с1
; 5
wx
wy
D 2
2
x
y
y
x
• Пограничный слой – область течения, прилегающая к обтекаемой
поверхности, в пределах которой происходит изменение параметра
течения (скорости, температуры или концентрации) от значения в
набегающем потоке до значения на обтекаемой поверхности.
199.
• Основные положения теории пограничного слояосновываются на условии, что толщина пограничного слоя
существенно меньше длины обтекаемой поверхности L.
<<L;
1; Масштабы величин
L
__
__
__
w x 1; x 1; w y ; y
Оценка порядка членов уравнений
Уравнения движения:
2
2
w x
w x
1 p
wx wx
wx
wy
2
2
x
y
x
x
y
1
1
1
1
1
12
1
<<
1
; 6
__ 2
2w y 2w y
w y
w y
1 p
p
wx
wy
0; 7
2
2
__x
y
y
y
y
x
__
1
1
__
__
__
__
12
__
__ 2
200.
• Уравнение неразрывностиw x w y
0 ; 8
x
y
1
1
__
__
• Уравнение теплопереноса
2T 2T
T
T
wx
wy
a 2 2 ; 9
x
y
y
x
1
1
1
1
1
<< __ 2
2
1
1
• Уравнение массопереноса
2 c1 2 c1
с1
с1
wx
wy
D 2 2 ; 10
x
y
y
x
1
1
1
1
1
1
<< __ 2
2
1
201.
• Исключение членов малого порядка позволяет упроститьсистему уравнений тепло- массопереноса, которая в
приближениях пограничного слоя имеет следующий вид
w x
w x
1 p
2w x
wx
wy
;
2
x
y
x
y
p
0;
y
w x w y
0 ;
x
y
T
T
2T
wx
wy
a 2 ;
x
y
y
с1
с1
2c1
wx
wy
D 2 ;
x
y
y
202. Условия применимости уравнений конвективного тепло- и массопереноса в приближениях пограничного слоя
• Приведем систему уравнений конвективного тепло-массопереноса длябезградиентного течения p 0 к безразмерному виду используя
x
следующие безразмерные величины:
wx
w
;
w
'
x
w y
x
w
; x ;
w L
L
'
y
Уравнение
движения
'
__
y
c1w c1
Tw T
c
;
y ;
1
;
c1w c1
Tw T
'
w 2 ' w 'x w 2 ' w 'x
w 2 w 'x
wx
wy
2
;
2
'
'
'
L
x
L
y
y
w L L L2 1
2
;
2
2
w L Re L
'
'
2 '
2
w
w
wx
L
1
'
'
x
x
wx
wy
2
;
'
'
2
x
y
Re L y '
203.
• Уравнение теплопереноса2
w
w
a
'
'
Tw T w x '
Tw T w y ' 2 Tw T '2 ;
L
x
L
y
y
2
a L L L
1
2
;
2
w L Re L Pr
2
2
L
1
'
'
wx ' wy ' 2
;
2
x
y ReL Pr y '
• Уравнение массопереноса
__
__
__
2
w
c
w
c
D
1
c1w c1 w 'x 1' c1w c1 w 'y ' 2 c1w c1 c'21 ;
L
x
L
y
y
D L L a L2 Le
2
;
2
w L a ReL Pr
__
w 'x
__
D
Le
a
2
число Льюиса
2
__
c1
L Le c 1
' c1
wy
2
;
'
'
2
x
y
Re L Pr y '
204.
Из условия что(Основного положения теории
0,1
пограничного слоя <<L; )
L
L2
1
1
1
;
2
L
Re L
Re L
Re L 100
L2
1
1
1
;
2
L
Re L Pr
Re L Pr
Re L Pr 100
L2 Le
Le
1
;
2
L
Re L Pr
Re L Pr
Le
0,01
ReL Pr
Условия применимости
уравнений конвективного теплои массопереноса в
приближениях пограничного слоя
205. Условия тройной аналогии процессов течения и тепло- массопереноса
• Уравнения тепломассопереноса при движении сред вбезразмерном виде
'
'
2 '
2
w
w
wx
L
1
'
'
x
x
wx
wy
2
;
'
'
2
'
x
y
Re L y
2
2
L
1
w 'x ' w 'y ' 2
;
2
x
y ReL Pr y '
__
w 'x
__
2
2
__
c1
L Le c 1
' c1
wy
2
;
'
'
2
'
x
y
Re L Pr y
• Уравнения становятся полностью аналогичными при
следующих условиях
1) Pr=1;
2)Le=1;
206. Пример использования аналогии между процессами тепло- и массопереноса
• Определение связи между коэффициентами тепло- и массоотдачиW ,
T , y
C1
dQ qdF;
dQ
0
L
Tw , C1 w
dM1
dx
x
d M1 m1 dF;
GcdT
Vdc1
dQ d M1
G V;
;
;
T Tw c1 c1w
q
m1
при выполнении условий аналогии
__
__
dc1
dT
d c 1;
d d c 1
d ;
c1 c1w
T Tw
c
207. МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ КОНВЕКТИВНОГО ТЕПЛО- И МАССОПЕРЕНОСА
208. Классический метод, основанный на тройной аналогии процессов течения, тепло- и массопереноса и приведении дифференциальных
уравнений вчастных производных к уравнениям в полных производных
Для безградиентного течения в приближениях пограничного слоя система
уравнений, описывающих тепло- и массоперенос на обтекаемой поверхности
имеет вид
2
w x
w x
wx
wx
wy
;
2
x
y
y
W ,
y
T ,
C1
0
L
Tw , C1 w
T
T
2T
wx
wy
a 2 ;
x
y
y
x
w x w y
0 ;
x
y
с1
с1
2c1
wx
wy
D 2 ;
x
y
y
209.
• При соблюдении условий аналогии достаточно получитьрешение одно из уравнений второго порядка, т.к.
c1 c1
wx
T T
w Tw T c1w c1
Введение вспомогательной функции η и функции тока ψ,
для которых выполняются следующие соотношения
wx
;
y
w
y
x
wy
;
x
• позволяет получить следующие зависимости:
уравнение неразрывности обращается в тождество
w x dy;
0
x
dy
d ;
w
w x dy w
0
2 2
0
x y y x
x w x
wx
d w x
d ;
w 0 w
w
0
210.
• Введем функциюwx
f ( )
d
w
0
wx
f ( )
w
'
• подстановка которой в уравнение движения приводит к
дифференциальному уравнению
f f 2f 0
''
'''
• граничными условиями для него являются следующие
уравнения:
0
f' f 0
f ' 1
• решение его находится численным методом имеет
следующий графический вид
211.
• график изменения относительной скоростиwx
w
1,0
wx
5
0,99
w
0,8
0,6
w
y
x
0,4
0,2
0
5,0
w
x
1,0
3
4
5
• откуда получается зависимость для толщины ламинарного
пограничного слоя
x
5,0
w
5,0
5
;
x
w x
Re x
212.
• плотность конвективного теплового потока к обтекаемойповерхности
T
T
q к к (Т Tw ) ;
Tw T
;
y
y
y y 0
w ''
w
f 0 0,332
;
y y
x
x
w
к 0,332
;
x
5,0
x
w
• толщина пограничного слоя возрастает
,а
коэффициент теплоотдачи убывает по координате x.
к
к
x
213.
• Безразмерный коэффициент теплоотдачиw
x
Nu x 0,332
0,332 Re x
x
x
Nu x к
• Средний по поверхности коэффициент теплоотдачи
L
L
1
1
w
w
к к dx 0,332
dx 0,664
L0
L0
x
L
__
• Безразмерный средний по поверхности коэффициент
теплоотдачи
__
к L
Nu
0,664 Re L ;
___
214.
• Определение параметров массоотдачиС1
C1
C1
С 1W D
D C1 C W
y
y
W
y
x
C1 C1
W
f 0
y
y
x
W
0,332D
x
x
Nu D
0,332 Re x
D
L
W
1
0,332D
0,664D W L
dx
dx
L0
L
x
L
Nu D
L
0,664 Re L
D
215.
• результаты для турбулентного пограничного слояЛаминарный
участок
Турбулентный пограничный слой
Re кр 5 10 5
x
T 0,37 0, 2
Re x
Nu x 0,03 Re
0 ,8
Nu L 0,037 Re
Pr
0 ,8
0 , 43
Pr
Pr
PrW
0 , 43
Pr
PrW
0 , 25
0 , 25
216. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
• Определить количество теплообменных панелей, необходимых длягазификации жидкого азота с расходом 0,1 кг/с при обдуве панелей
наружным воздухом со скоростью 1 м/с при Т∞=233 К
газообразный
азот
Теплофизические параметры азота:
Температура кипения при атмосферном давлении 77 К
ra=199200 Дж/кг; Pr=0,728; с=1000 Дж/(кг К);
ν=10-5 м2/с
2м
w
Определение числа Рейнольдса: wL/ν=1•1/10-5
Re=105<Reкр=5•105 - ламинарный погранслой
__
___
Nu
жидкий
азот
1м
0,5
к L
0, 33
0,664 Re 0L,5 Pr 0,33 0,664 10 5 0,728 189;
___
__
к
Nu 189 0,0212
Вт
4 2 ;
L
1
м К
217.
• Тепловой поток, подводимый к поверхностям одной панелиQ к к (Т Tw )F 4 233 77 2 (2 1) 2496Вт;
• Количество панелей для получения требуемого расхода азота
G a ra 0,1 199200
n
8
Qк
2496
• Минимальное расстояние между панелями ∆min=2 δ
L
1 10
5,0
5
w
1
∆min=2 δ= 0,0316 м
5
0,0158м
218. ТЕПЛООБМЕН НЕОГРАНИЧЕННЫХ И СТРУЙНЫХ ПОТОКОВ С ПРЕГРАДАМИ
219. Теплообмен неограниченных потоков газа с преградами
• Помимо рассмотренного ранее теплообмена плоских поверхностей сосредой, движущейся параллельно поверхности, в технике большое
значение имеют варианты взаимодействия потоков с поверхностями,
расположенными под некоторым углом к движущейся среде
• Потоки, действующие на преграды подразделяются на
неограниченные и струйные
• К неограниченным потокам относятся потоки воздуха, возникающие при
действии ветра (или движении конструкции в воздушной среде,
например при перемещении передвижной ПУ)
W∞
220. Параметры теплоотдачи при натекании неограниченного потока на преграду
• Ламинарный пограничный слой. Плоский поток.Пограничный
слой
L
W∞,T∞
0
L
Пограничный
слой
x
Критическая точка
(скорость потока 0)
Wx U1x
W
U1 2
2L
q к к w
Wx x
Re x
Nux = 0,57 Rex0,5 Pr0,4
Nu
к
x
221.
• Ламинарный пограничный слой. Осесимметричный поток.Wx U1x
сфера
плоскость
3W
U1
D
W
U1 2
2L
q к к w
D=2L
Wx x
Re x
Nux = 0,763 Rex0,5 Pr0,4
Nu
к
x
222.
• Турбулентный пограничный слой.– Плоский поток
Nux = 0,57 (1+0,328b) Rex0,5 Pr0,4;
– Осесимметричный поток
Nux = 0,763 (1+0,21b) Rex0,5 Pr0,4;
– Где
1
b 0,5 K W
U
1
– K – коэффициент пропорциональности, определяемый
экспериментально;
– ε∞ - масштаб турбулентности
223. Струйные потоки газа
• Струйные течения газа широко распространены в ракетнокосмической технике: в реактивных двигателях, системахдренажа криогенных топливных и заправочных систем, в
вентиляционных устройствах и воздушных завесах систем
кондиционирования и воздушных систем
термостатирования, в газогорелочных устройствах,
двигателях, турбинах и т.д.
• Струей называют поток вещества, перемещающегося в
постоянном направлении на расстоянии многих своих
поперечных размеров
• В основе классификации струйных течений лежат четыре
основных признака:
–
–
–
–
механизм распространения;
признак сжимаемости;
признак однородности;
условия внешней среды и струи.
224.
• Механизм распространения. В этом случаеподразумевают механизм переноса импульса,
энергии и вещества в струях. По этому признаку
струи различают ламинарные и турбулентные.
• Физика ламинарных течений в настоящее время
изучена достаточно полно – это молекулярное
трение, теплопроводность и диффузия. Для
ламинарных струй построена строгая
математическая модель.
• Физика турбулентных течений в основном
изучается на базе экспериментальных
исследований. В теоретическом плане созданы
полуэмпирические и эмпирические теории.
Интенсивно развиваются статистические методы
описания турбулентности.
225.
• Признак сжимаемости. По этому признаку струиделятся на несжимаемые и сжимаемые.
• Струи несжимаемой жидкости – это струи, в
которых изменение плотности вещества
незначительно (ρ=const). К ним относятся струи
капельной жидкости (вода) и газовые струи при
малом изменении плотности (при дозвуковых
скоростях, малых перепадах температур; при
близких значениях молекулярного веса газа в
струе и окружающем пространстве).
• Струи сжимаемой жидкости – это сверхзвуковые
струи, а также струи при значительных изменениях
температуры и вязкости, трансзвуковые течения
(число Маха М=1).
226.
• Признак однородности. По этому признакуразличают струи однородные по составу (газ или
жидкость), неоднородные смеси (газов, жидкости,
твердых частиц и т.д.), струи плазмы и струи
электропроводящей жидкости.
• Условия внешней среды и струи. Этот признак
включает следующие условия:
• 1) вид движения струи и среды;
• 2) геометрию окружающего пространства;
• 3) величину поперечного градиента давления в
струе.
• По виду движения струи и среды струи
классифицируют следующим образом:
• а) затопленные струи;
• б) струи в однородном потоке (спутном, встречном,
ориентированным под углом);
• г) свободные струи.
227.
• З а т о п л е н н ы е с т р у и – это струи, истекающие вбезграничное пространство, заполненное жидкостью или
газом тех же физических свойств, что и в самой струе. Это
пространство называют затопленным или неподвижным
(ν1=0).
• Для затопленной струи характерно ее расширение по мере
удаления от сопла в силу ее эжекционной способности. В
случае турбулентного течения границы струй всегда
прямолинейны. Этот класс струй обладает «дефектом
памяти», заключающегося в том, что струя на достаточно
большом расстоянии от источника «забывает» особенности
самого создавшего ее источника. Из опыта известно, что
струя, истекающая из квадратного, треугольного,
крестообразного и других форм отверстий на достаточном
удалении от источника обладает свойствами струи,
истекающей из круглого отверстия.
228.
• Струи в однородном потоке(спутном, встречном, ориентированном под
углом к основному потоку).
• На рис.представлена схема струи, которая
вытекает из источника в пространство,
заполненное движущейся равномерно со
скоростью ν1>0 жидкостью тех же физических
свойств, что и в самой струе. Причем, сопло
ориентировано таким образом, чтобы направление
формируемого им потока совпадало с
направлением движения ν1, т.е. движение струи
сопровождается спутным движением жидкости в
пространстве.
• На рис. представлена схема струи, вытекающей во
встречный однородный поток (ν1<0).
229.
• С в о б о д н ы е с т р у и - это струи,истекающие в пространство, заполненное
жидкостью или газом физических свойств,
отличных от свойств жидкости в самой струе.
• Примером свободной струи является
высоконапорная струя воды в воздухе. Этот тип
струй широко применяется для распыливания
жидкости. В распыленном виде сжигают жидкое
топливо, распыленной жидкостью охлаждают
горячие газы истекающие из сопел ракетных
двигателей для снижения теплового воздействия
на поверхности стартовых систем ракетных
комплексов.
230.
• По геометрии окружающего пространства классифицируют струиследующим образом:
• а) полуограниченные;
• б) несвободные;
• в) струйное обтекание тел.
• Полуограниченные струи – это струи, движущиеся вдоль твердой
поверхности.
• Поверхность может быть также перфорированной (пористой), через
которую может нагнетаться или отводиться газ.
• Полуограниченные струи могут развиваться и в спутных и во встречных
потоках.
• Полуограниченные струи применяются для тепловой защиты
поверхностей от воздействия внешнего потока.
• Несвободные струи – это струи, вытекающие в полуограниченное или
ограниченное (стесненное) пространство.
• К ним относятся настильные струи (тепловая завеса, металлургические
печи и др.) и струи, истекающие в канал с односторонним или
двухсторонним расширением. Этот класс струй применяется также в
камерах сгорания турбореактивных двигателей, топках котлов, в печах.
• При струйном обтекании тела за его кормой возникает характерная
область возвратных течений.
231. Структура затопленной турбулентной струи.
• При турбулентном движении, как известно, наряду сосевым движением существует и поперечное движение
частиц.
• За счет турбулентных пульсаций частицы попадают за
пределы струи и переносят в граничащие со струей массы
неподвижного воздуха свое количество движения, увлекают
(эжектируют) эти массы, придавая им определенную
скорость.
• На место ушедших из струи частиц в нее попадают
частицы из окружающего воздуха, которые
подтормаживают граничные слои струи. Следствием этого
обмена импульсами между струей и неподвижным
воздухом является возрастание массы струи и убывание
скорости у ее границ.
232.
• Подторможенные частицы струи вместе с увлеченными частицамиокружающего воздуха образуют турбулентный пограничный слой,
толщина которого по мере удаления от выходного отверстия
возрастает. Соприкасаясь с внешней стороны с неподвижной средой
(ν=0), а с внутренней – с ядром постоянной скорости (ν=ν0),
пограничный слой приобретает переменный профиль скоростей
• Ядро постоянной скорости по мере удаления от выходного отверстия и
утолщения пограничного слоя сужается, пока полностью не исчезнет.
После этого пограничный слой уже заполняет все сечения струи,
включая и ось потока. Дальнейшее размывание струи сопровождается
не только возрастанием ее ширины, но и падением скорости на оси.
v0
Турбулентный погранслой
d0
1
V Ядро постоянной скорости
V0
Начальный участок струи
Основной участок струи
x
d0
233.
• Как показывают опыты, границы струи, как внешняя, так и ядрапостоянной скорости, прямолинейны. Точка 0 пересечения внешних
границ струи называется полюсом струи.
• Статическое давление в разных точках струи изменяется
несущественно и приблизительно равно давлению в окружающем
пространстве, т.е. свободную струю можно считать изобарической.
х0
0
v0
d0
хн
α
• Как показали теоретические и экспериментальные исследования
основные параметры струи зависят от коэффициента турбулентности а,
характеризующего интенсивность перемешивания и зависящего от
конструкции насадка, из которого вытекает струя. Чем больше
коэффициент турбулентности, тем интенсивнее перемешивание и
больше угол одностороннего расширения струи α.
234.
Коэффициент турбулентности а и угол расширения 2α турбулентной струи
Тип выпускного насадка
Плавно выполненное сопло
Цилиндрическая труба
Внешний цилиндрический
Конически расходящийся
Плоский при отношении
его высоты к длине:
1:20
1:10
а
0,066
0,07
0,076
0,08
0,1 – 0,15
0,09 – 0,14
2α
25о40΄
27о
29о
• Основные параметры затопленной турбулентной струи можно
определить по следующим формулам.
– Расстояние x0 от полюса до входного отверстия:
• Круглая струя
– х0=0,15d0 /a
плоская струя
х0=0,41b0/a
– где d0 – диаметр отверстия или насадка;
b0 – половина высоты устья плоского насадка.
– Длина начального участка хн струи:
• Круглая струя
– хн= 0,335d0 /a
плоская струя
хн= 1,03 b0 /a
235. Теплообмен струйных потоков газа с преградами
• При перпендикулярном натекании струйного потока напреграду от критической точки (V=0) в радиальном
направлении образуется осесимметричное течение газа с
образованием областей ускоренного и замедляющегося
течения со скоростью Wr
При расстояниях меньше h<x
d0
h
V0
h
h
do
r
r
do
u odo
Re o
Wr
r h
*
h 6
Для области критической точки
Nu 1,6 Re Pr
0, 5
o
0, 33
0,11
/h
Для области ускоренного течения
Nu 1,6 Re Pr
0,5
r*
н
0,1
r
0 , 33
r
1 0, 2
0,11
3h h
236.
При расстояниях больше h>xн, h 6r* 0,34 h
0, 7
Для области критической точки
Nu 5,25 Re 0,5 Pr 0 / 33
h
0, 77
Для области ускоренного течения
2
r
0,5
0 , 33
Nu 5,25 Re Pr
1 2,92 0, 25
0 , 77
h
h
237. Структура сверхзвуковой струи
• На начальном участке сверхзвуковая струя имеет сложную структуруКриволинейный скачок уплотнения
Свободная граница струи
Прямой скачок уплотнения
Волны разряжения и сжатия
Конический скачок уплотнения
р
рн
М
∆р
∆М
1
Длина одной «бочки» ≈ 3d0; Начальный участок включает в себя 10-12 «бочек»
На основном участке изменение параметров струи происходит плавно.
238.
• Теплоотдача сверхзвуковой струи на преградеNu х 1,08 1 0,6 k
0 , 52
0 , 52
Mx
0 ,8
Re х
0 , 27
Re
0,5
х
Pr 0, 4
– где k – коэффициент учитывающий расположение
преграды по отношению к струе (k=1 при ┴
расположении; k=0 при ║ расположении преграды);
– ε – масштаб турбулентности
• Экспериментальный метод определения
теплоотдачи при натекании струи на преграду
Twi
Tвхi
Q i G i c ж Т вых ш Т вх i
Tвыхi
Q
q к Tf* Tw
F
к 1
Tf* Tf 1
M2
2
239. ТЕПЛОВАЯ ЗАЩИТА КОНСТРУКЦИЙ ОТ ВЫСОКОТЕМПЕРАТУРНЫХ ПОТОКОВ ГАЗОВ
240. Параметры теплового воздействия, обусловленного взаимодействием сверхзвуковой струи с поверхностями конструкций
• При перпендикулярном натекании струи на преградуTf – температура в струе до висячего скачка уплотнения
Tf* - температура торможения потока
к 1
T Tf 1
M2
2
*
f
к=ср/сv – показатель адиабаты для газа
Tf
Tf*
Tw
q к к T Tw
*
f
241.
• При взаимодействии под углом и для участков течениявдоль поверхности в расчетах конвективного теплообмена
используется значение температуры восстановления
потока Tfw
q к к T fw Tw
Tfw
к 1 2
Tf 1 rB
M
2
rв – коэффициент восстановления
потока:
для ламинарного погранслоя
rB Prf
для турбулентного погранслоя
Tfw
rb 3 Prf
242.
• Уровни плотностей тепловых потоков к поверхности ивремя воздействия
Время воздействия при старте:
в
2 L сз L 0 d a
(n 1)g
L сз – относительная длина сверхзвукового
участка струи (30 – 36);
L 0 – относительное начальное
расстояние сопла от преграды (3 – 4);
n – перегрузка ракеты при старте.
На практике время воздействия составляет
3 – 10 с (до 10 мин при наземной отработке
двигателей)
243. Методы тепловой защиты конструкций
• Охлаждениеконструкций:
– конвективное;
– пористое;
– пленочное;
– заградительное;
– комбинированное;
• Теплозащитные
покрытия:
– тугоплавкие;
– аблирующие:
• оплавляющиеся
• сублимирующиеся
• коксующиеся
244.
• Параметры конвективного охлажденияq к т Tfw Tж
Tf
T2
Tж
T1
1
Kт
1
1
ж ср к
q ж T1 Tж
q
T1 Tж
ж
1
q
T2 T1 T2 T1
q
Tж q
ср
ж ср
1 Tж 2 ж ( способы понижения температуры Т2 )
ср
245.
• Параметры пористого охлажденияУравнение теплового баланса на поверхности
конструкции со стороны газового потока
Tf
f
I r I w g a i ж
с pw
I w c p Tw
I r с p Tfw
w
Tж
i ж с ж Tw Tж rж
Tw
Ir
- полная энтальпия газа на удалении от
поверхности;
Теплоемкости:
Iw - полная энтальпия газа на поверхности;
ср – газа при
температуре Tfw;
Χ – удельная теплота догорания топлива в струе (5 -10
% от теплотворной способности топлива)
срw – газа при
температуре Tw;
gа – удельный расход охлаждающей жидкости (кг/(с
м2))
cж – охлаждающей
жидкости
rж – удельная теплота испарения охлаждающей
жидкости
246.
• Определение расхода жидкости дляпористого охлаждения
rж
кДж
;
кг
кДж
метанол 1120..
;
кг
кДж
этанол 873..
кг
вода 2260..
ga
f
I fw I w
c pw
c ж Т 2 Т ж rж
при с p с pw
0
f Tfw Tw
ga
с ж Т w Т ж rж
Т w Т кип ж
• Преимущества пористого охлаждения:
– Температура конструкции может быть на уровне температуры
испарения охлаждающей жидкости
– Минимальный потребный расход жидкости на охлаждение
• Недостатки:
– Сложная и дорогостоящая технология изготовления
– Необходимость высокой степени очистки охлаждающей жидкости
247.
• Параметры пленочного охлажденияУравнение теплового баланса на поверхности
конструкции со стороны газового потока
Tж
f
I r I w h l G a i ж
c pw
I r с p Tfw
Tf
i ж с ж Tw Tж rж
Tw
l
I w c p w Tw
Ir
- полная энтальпия газа на удалении от
поверхности;
h
Iw - полная энтальпия газа на поверхности;
Χ – удельная теплота догорания топлива в струе
(5 -10 % от теплотворной способности топлива)
Ga
Gа – расход охлаждающей жидкости (кг/с)
Варианты каналов: 1) β=90°(возможен отрыв
пленки от поверхности, требуется ограничение
скорости подачи жидкости)
rж – удельная теплота испарения охлаждающей
жидкости;
2)β <15°(нет ограничений на скорость)
l – длина растекания пленки
β
248.
• Определение длины растекания пленки дляпленочного охлаждения
Ga iж
f
I r I w h
с pw
при с p с p w
0
Ga iж
f Т fw Tw h
Т w Т кип ж
249.
• Параметры заградительного охлажденияTf, W∞
T0, U0
b
x0
Θ
Tfw T
Tfw T0
х0
U0
0,107 0,037
b
W
1
Θ
x
при x х 0
1
1
2
3
U0
W
x
U0
U
0
1 W 2 W 3
1
W U 0
W U 0
250.
• Вариант заградительного охлаждения за счет ввода потокаохлаждающей жидкости в струи высокотемпературного
d0
газа
Соотношение массовых расходов
воды и газов:
Gж/Gг.>1,5
Расстояние до поверхности h=h/d0
h
h>6,5
для обеспечения полного
испарения жидкости в струе с
температурой смеси ≈ 900 °С
• Комбинированное охлаждение сочетает несколько видов
охлаждения, например, заградительного и конвективного
251. Теплозащитные покрытия
• Тугоплавкие покрытия используются для снижения температуры наповерхности основной конструкции при тепловом воздействии
q к т Tfw Tж
Т
Т
Тfw
Тfw
Тпл
Тпл
Тж
y
q
q ж T1 Tж T1 Tж
ж
Тж
δ
1
δп
23
кт
1
1
1
п
ж п f
y
1
q
q T2 T1 T2 T1 Tж q
ж
1
п
п
п
T3 T2 T3 T2 q Tж q
q
п
п
ж п
252.
• Требования к материалам тугоплавких покрытий– покрытие должно иметь высокую температуру
плавления (Тпл.п> T3);
– покрытие должно иметь коэффициент теплопроводности
ниже теплопроводности основной конструкции (λп< λ);
– покрытие должно иметь температурный коэффициент
объемного расширения одинаковый с температурным
коэффициентом объемного расширения основной
конструкции для исключения отслоения покрытия от
поверхности основной конструкции (αtп≈ αt)
• Материалы тугоплавких покрытий – окислы
металлов ( двуокись циркония) обладают низкой
ударной вязкостью, требуют применения
защитного демпфирующего слоя от действия
сосредоточенных нагрузок
253. Аблирующие покрытия
• Абляция – совокупность процессов, сопровождающихразложение покрытия под воздействием тепловых потоков
• Под действием теплоты аблирующее покрытие уносится с
поверхности, образуя защитный пограничный слой,
который оттесняет поток горячего газа от поверхности
Фронт уноса покрытия
Основные характеристики покрытия:
Та – температура абляции (температура начала
разложения и уноса покрытия)
I
rа – теплота абляции (Дж/кг) – количество теплоты,
необходимое для разложения единицы массы
покрытия;
ra
основная конструкция
I
покрытие
q
qвн
qл
ga
*
кг
2
м с
q q л q вн
ga
*
- удельный расход продуктов
разложения с поверхности покрытия
254.
• Для расчета процесса уноса покрытия удобнееиспользовать характеристику покрытия - эффективную
теплоту абляции
ra эф
q 0 q л q вн
ga *
– где q0 – плотность теплового потока к поверхности без учета
пограничного слоя защитного газа
f
I r I w
q0
сp w
q вн g a * с п Ta T0
Ta 4 Tf 4
q л п с 0
100 100
Т0 – начальная температура покрытия
4
4
f
Ta Tf
I r I w п c 0
с pw
100 100
ga *
ra эф c п Ta T0
255.
• Определение необходимой толщины покрытияg a * п u
ρп – плотность покрытия; u – скорость уноса
покрытия
• В общем случае необходимая толщина покрытия может
быть определена
п u d
0
q
0
q л d
0
п rэфa с п Ta T0
• При постоянной скорости уноса
п
q 0 q л
u
п rэф с п Ta T0
a
Ta 4 Tf 4
f
I fw I w п c 0
C pw
100 100
п rэфa с п Ta T0
256. Виды аблирующих покрытий
• Сублимирующиеся покрытия –покрытия,материал которых при воздействии
переходит из твердого состояния в
газообразное (материалы выполняются на
основе асбеста и применяются для
тепловой защиты конструкций из металлов)
• Асбестовые покрытия склонны к
растрескиванию при действии изгибных
нагрузок с образованием трещин
• В качестве ТЗП в случае исполнения
конструкций из стеклопластика
предпочтение отдается аблирующим
покрытиям, выполненным также на основе
стеклопластика со связующим
коксующимся материалом (коксующимся
покрытиям)
• Тепловая защита коксующихся покрытий
осуществляется за счет следующих
эффектов:
– разложения связующего материала с
образованием у поверхности потока газов,
оттесняющих воздействующий поток газа;
– образования частиц чистого углерода, которые
образуют теплоизоляционный слой,
уменьшающий приток тепла к силовой обечайке;
Схема коксующегося ТЗП
1
2
3
5
4
1-силовая обечайка; 2-ТЗП;
3- воздействующий поток
газа; 4-пористая
структура частиц
углерода; 5-поток газов,
образующихся при
разложении покрытия
257.
•После окончания воздействиятемпература покрытия имеет
значения ≈ 1000 °С и при
соприкосновении с воздухом
склонно к возгоранию (следует
исключить воздух например
подачей к поверхности азота
258. Примеры определения параметров тепловой защиты
• Определить параметры тепловой защиты для следующих параметровтеплового воздействия:
–
–
–
–
–
–
–
Температура в струе до преграды Тf = 2500 К;
Относительная скорость струи до преграды М=2,3
Теплофизические характеристики струи: к=1,2; Pr=0,56; ср=1500 Дж/(кгК);
Теплотворная способность топлива Нu – 7000 кДж/кг
Давление струи на поверхности конструкции рс = 106Па;
Коэффициент теплоотдачи струи на поверхности αf=4000 Вт/(м2К)
Время воздействия струи 7 с
• Расчет характеристик тепловой защиты:
– коэффициент восстановления струи на преграде (для турбулентного
погранслоя:
rв 3 Prf 3 0,560 0,824
– температура восстановления струи на преграде
Tfw
к 1 2
1,2 1 2
Tf 1 rB
M 2500 1 0,8244
2,3 3590.269 К
2
2
– температура охлаждающей воды: 20 °С сж= 4,183 кДж/(кгК)
– характеристики воды при давлении струи на преграде: - температура кипения Ткип 180 °С; удельная теплота кипения rж= 2015,2 кДж/кг; удельная теплоемкость
сж=4,417 кДж/(кгК)
259.
• Характеристики охлаждения:– Полное теплосодержание струи перед преградой:
I r с p Tfw
0,07H u
I r с p Tfw 1,5 3590,269 0,07 7000 5875.4035 кДж/кг
– теплосодержание струи на преграде
Т w Т КИП ж 180 273 453К
I w с p w Tw
I w C p w Tw 1,1 453 498,3
– удельный расход воды на охлаждение
f
I r I w
c pw
4000
5875,4 498,3
кг
1,1
ga
7.23 2
c ж Т w Т ж rж 0,5 4183 4417 180 20 2015200
м с
260.
• Толщина ТЗП с характеристикамип=2300 кг/м3; rэфа=6∙105 Дж/кг; Та=493 К;
сп=1200 Дж/(кг∙К)
Ta 4 Tf 4
493 4 2500 4
f
4000
I fw I w пр с 0
5875,4 498,3 0,9 5,67
с pw
1,1
100 100
100 100
п
7 0.077 м
п rэфa с п Ta T0
2300 600000 1200 493 293














































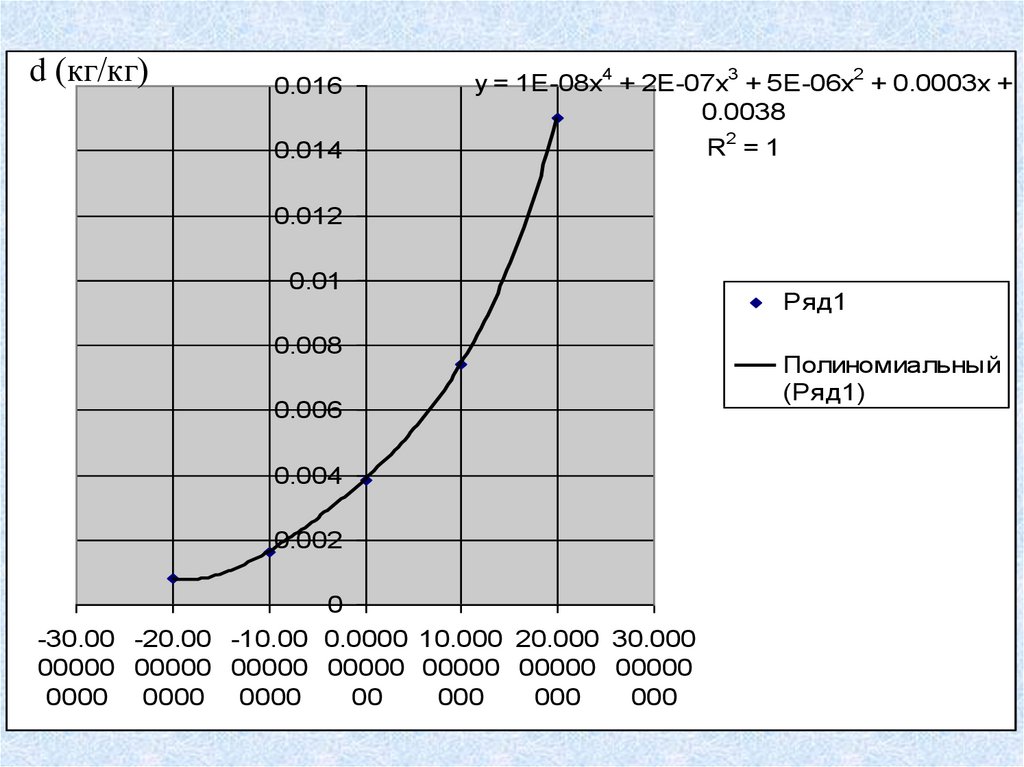





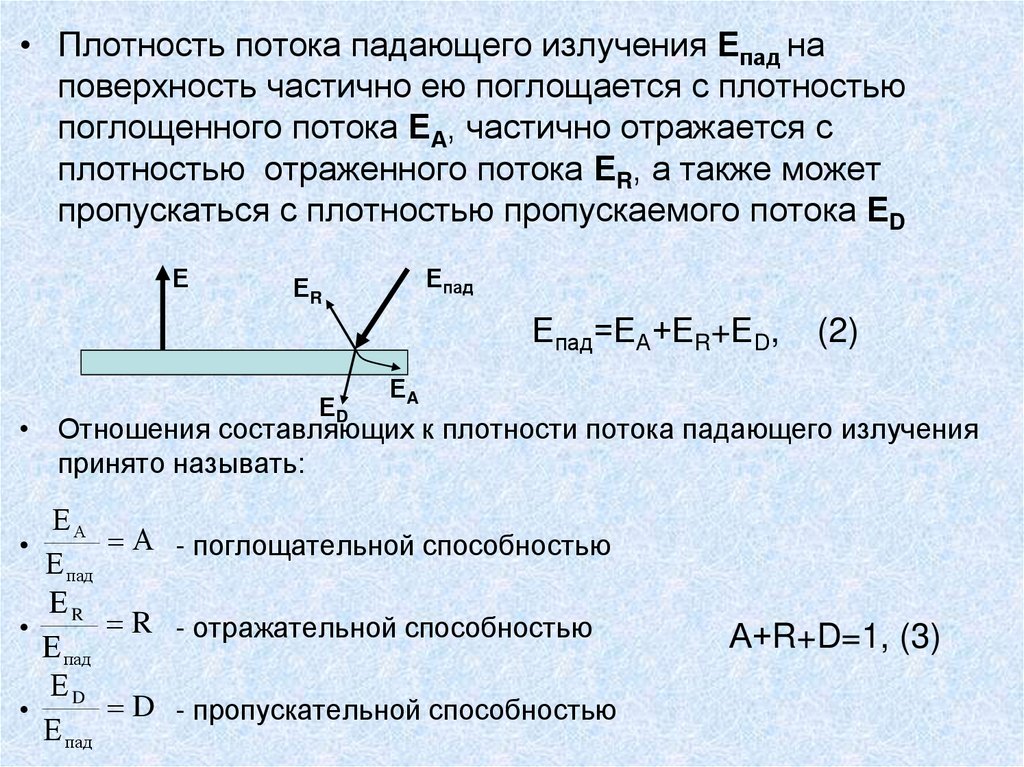













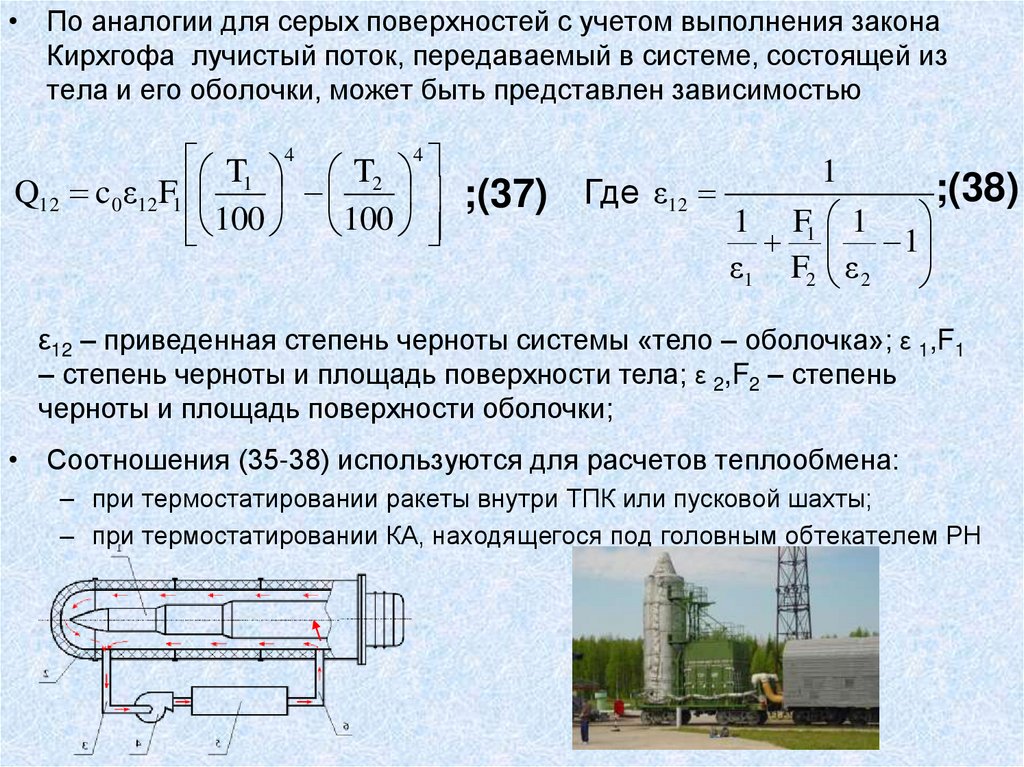



























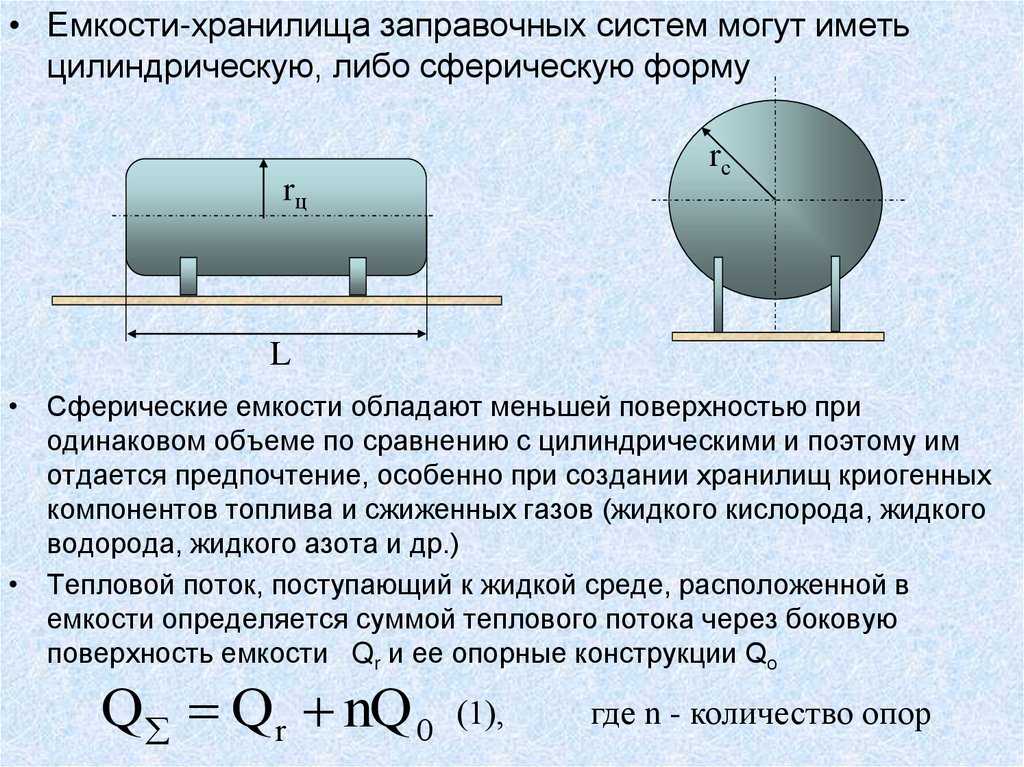























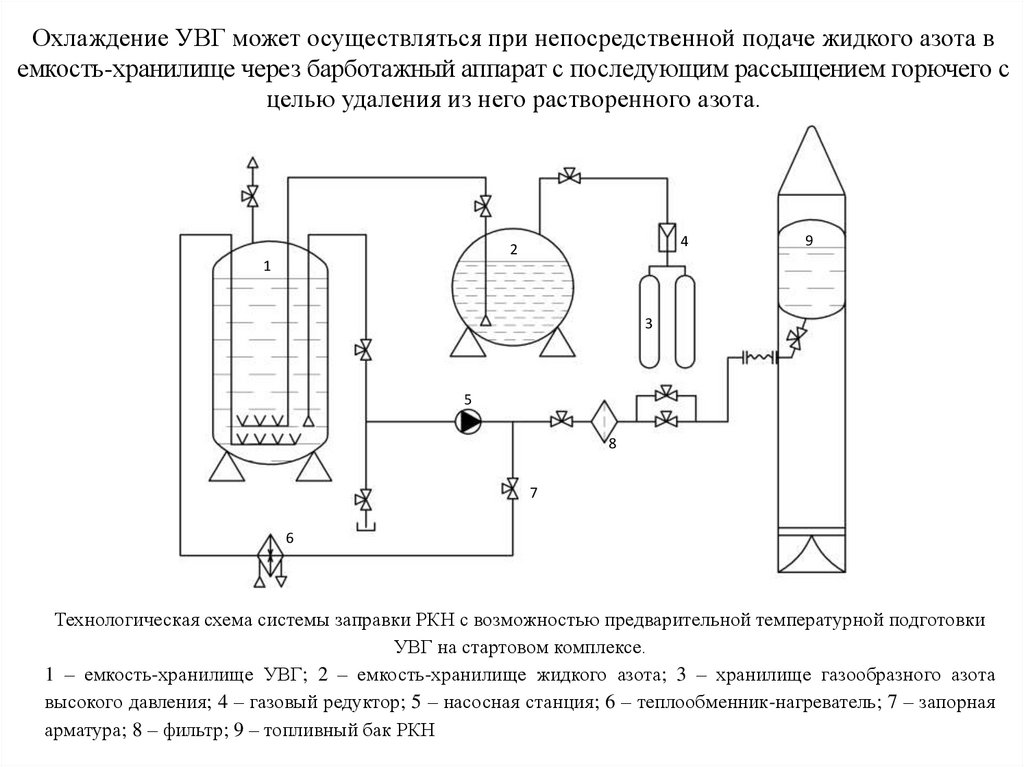





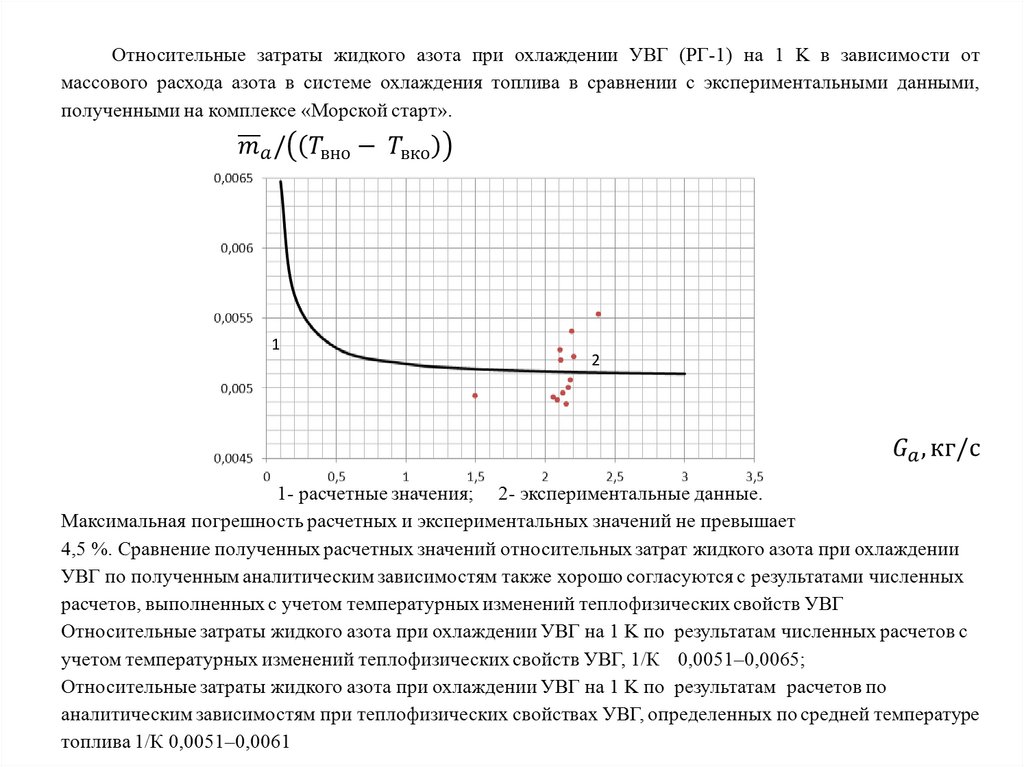




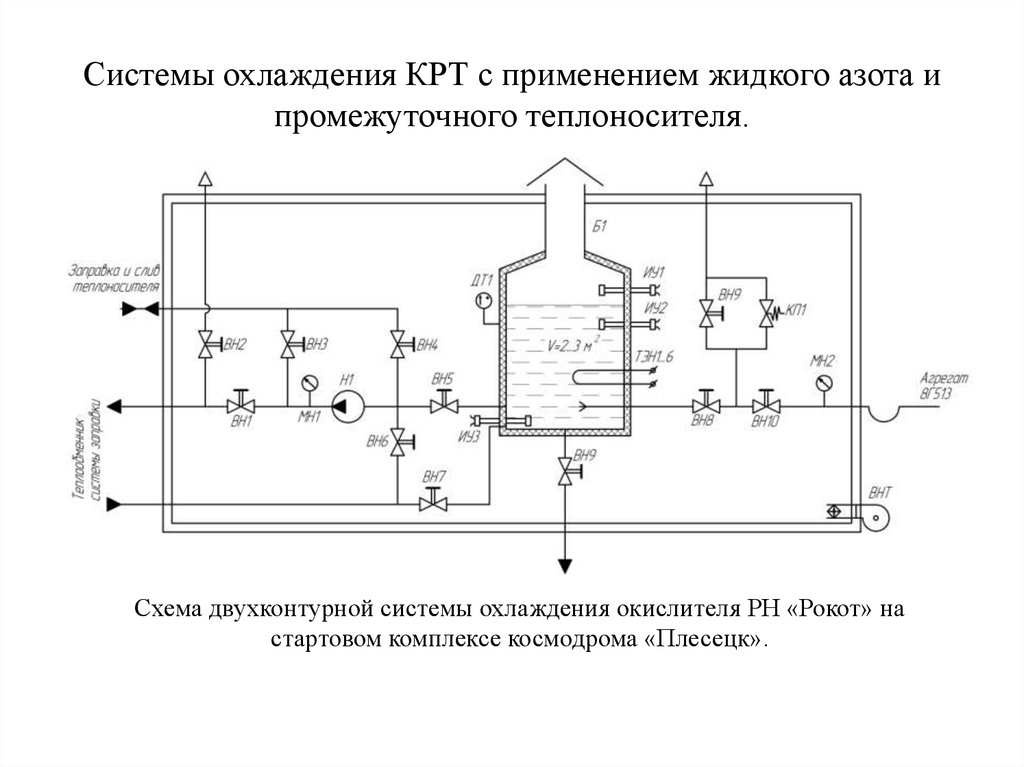
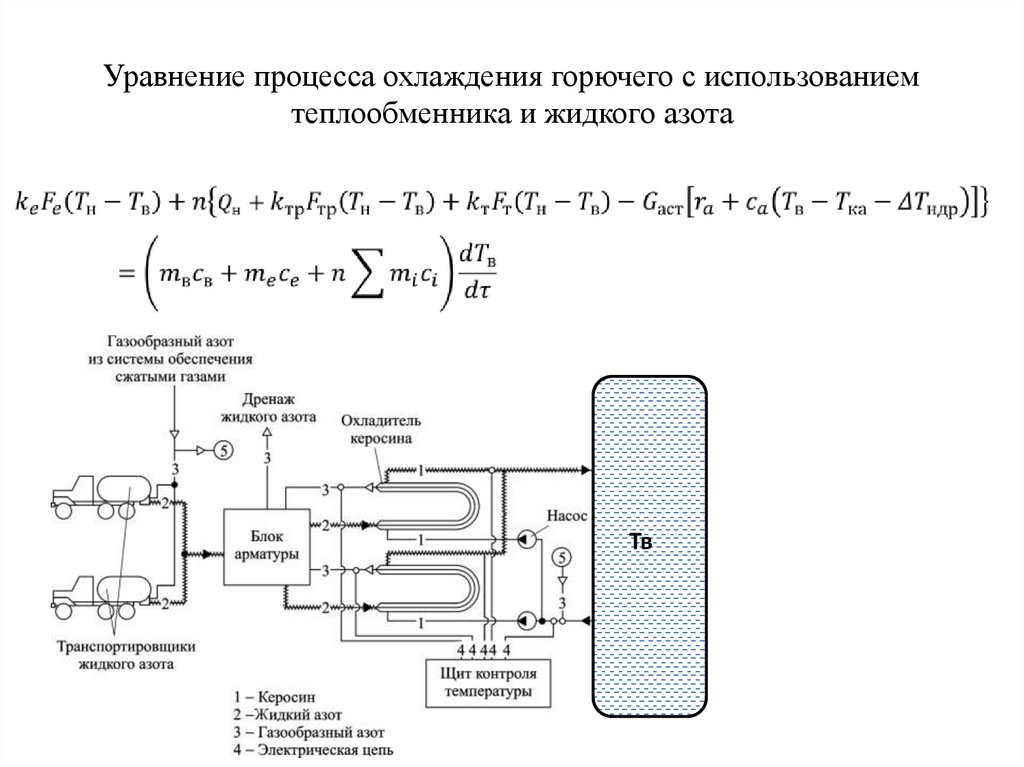

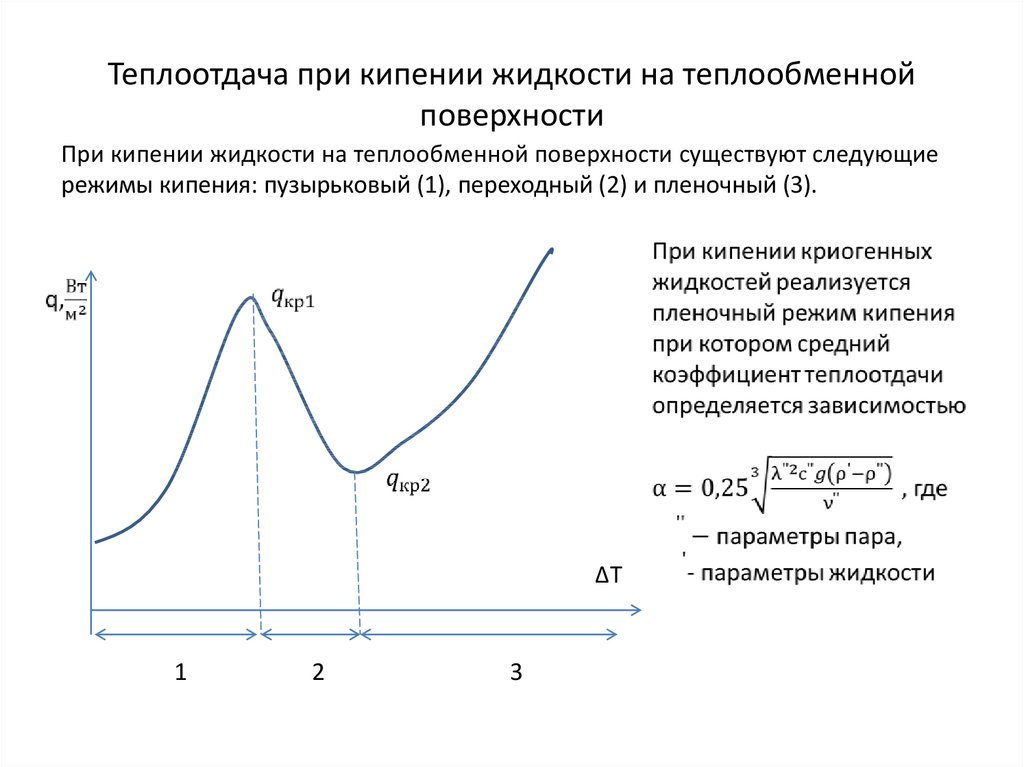



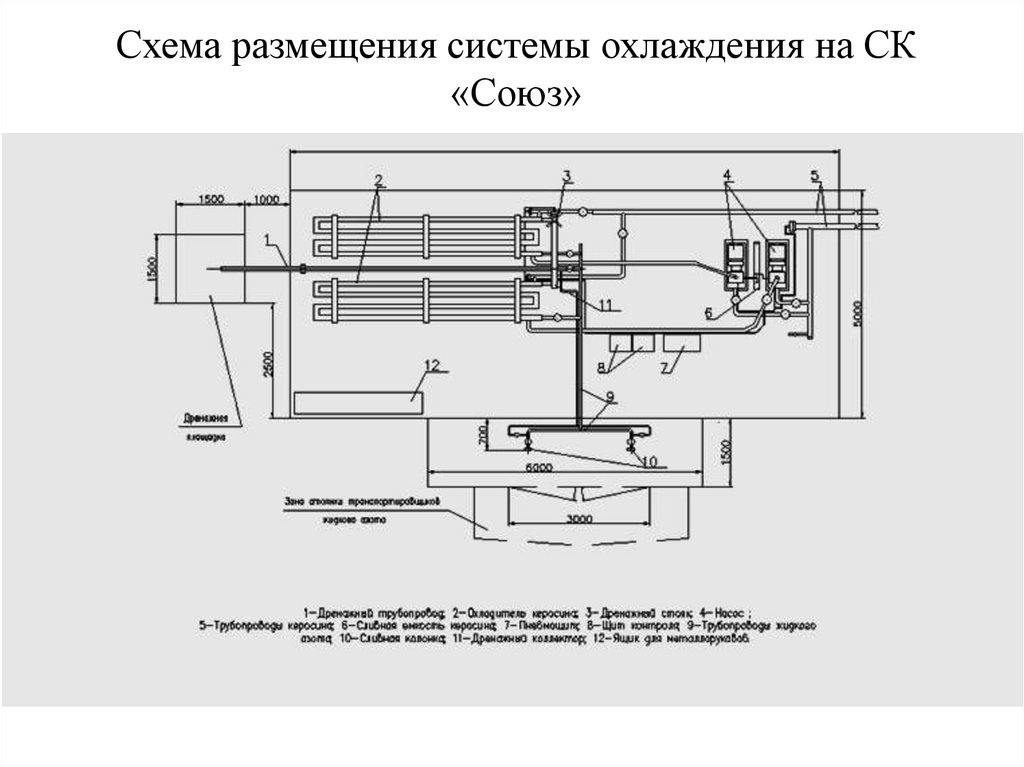
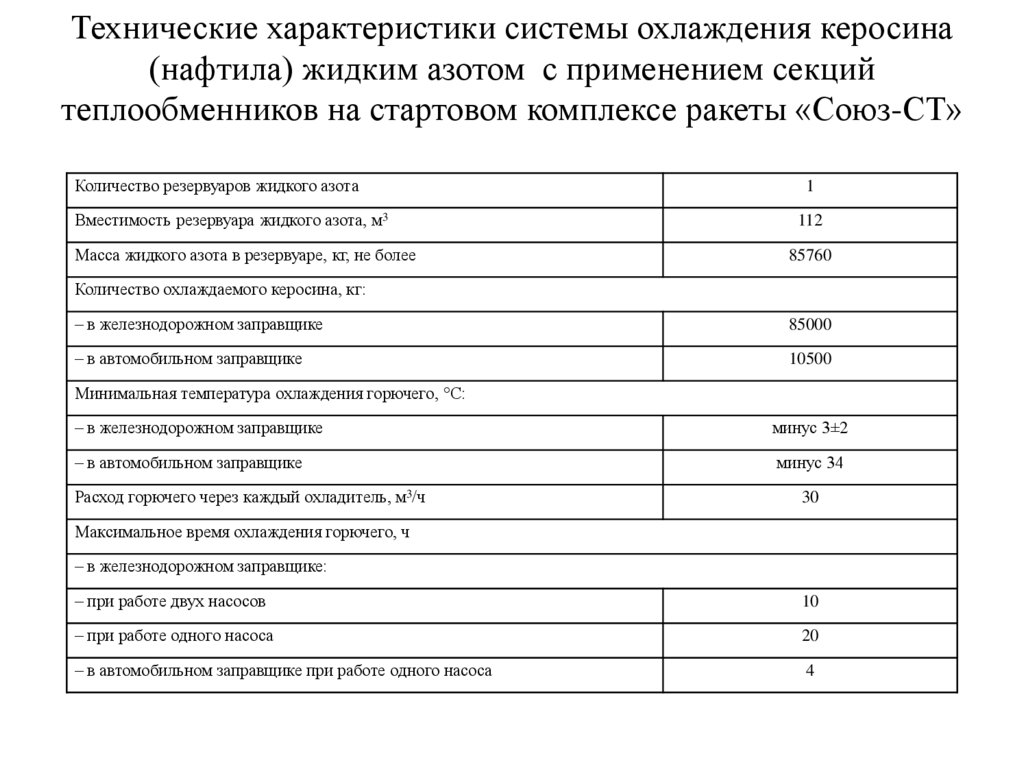

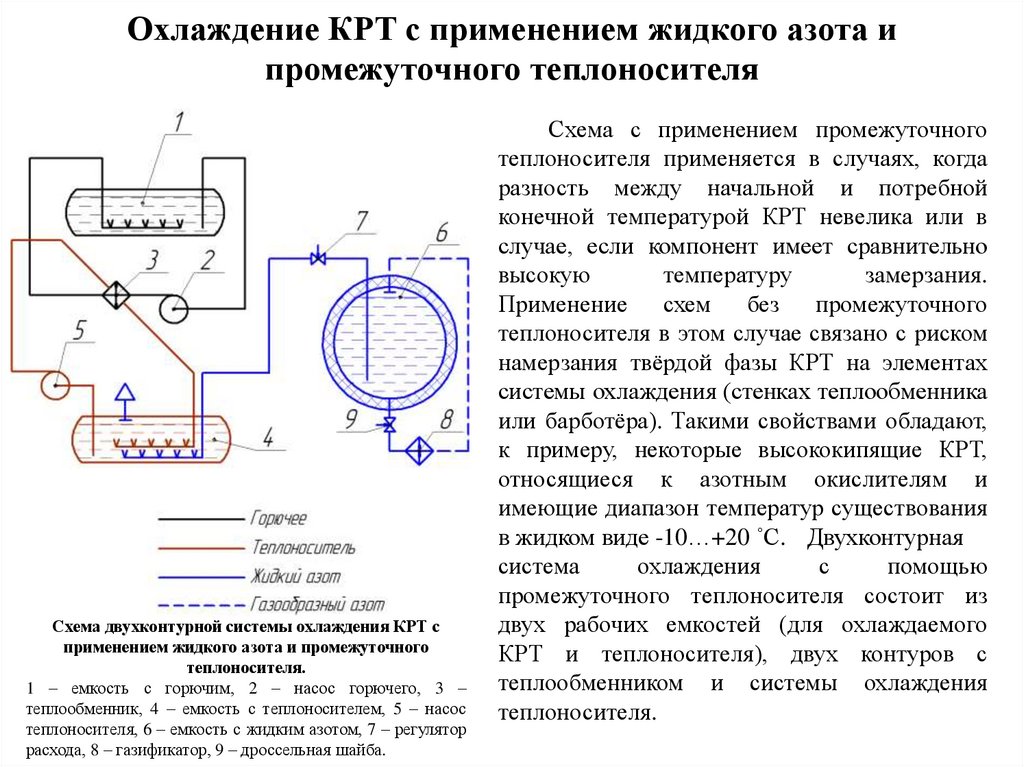













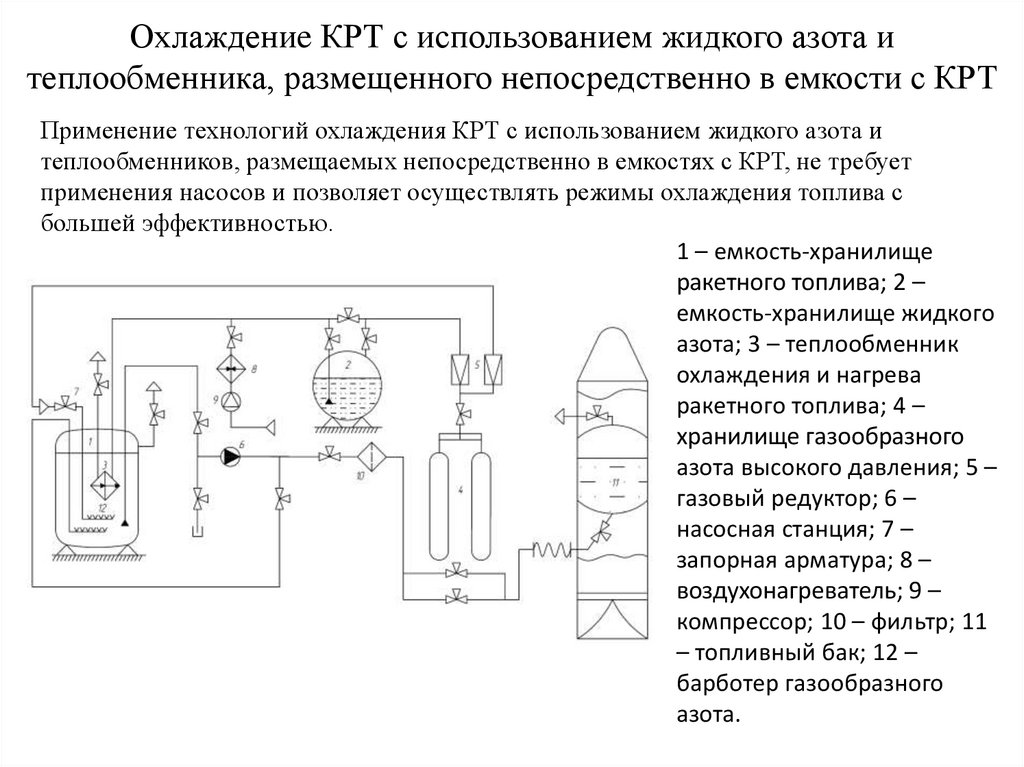



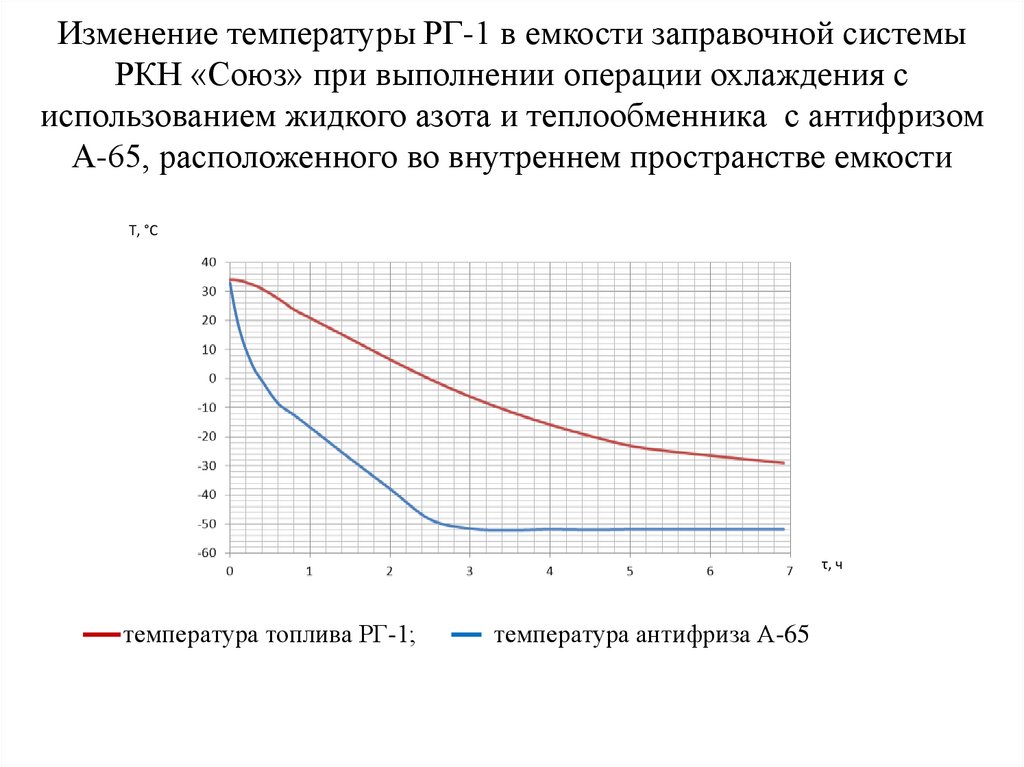














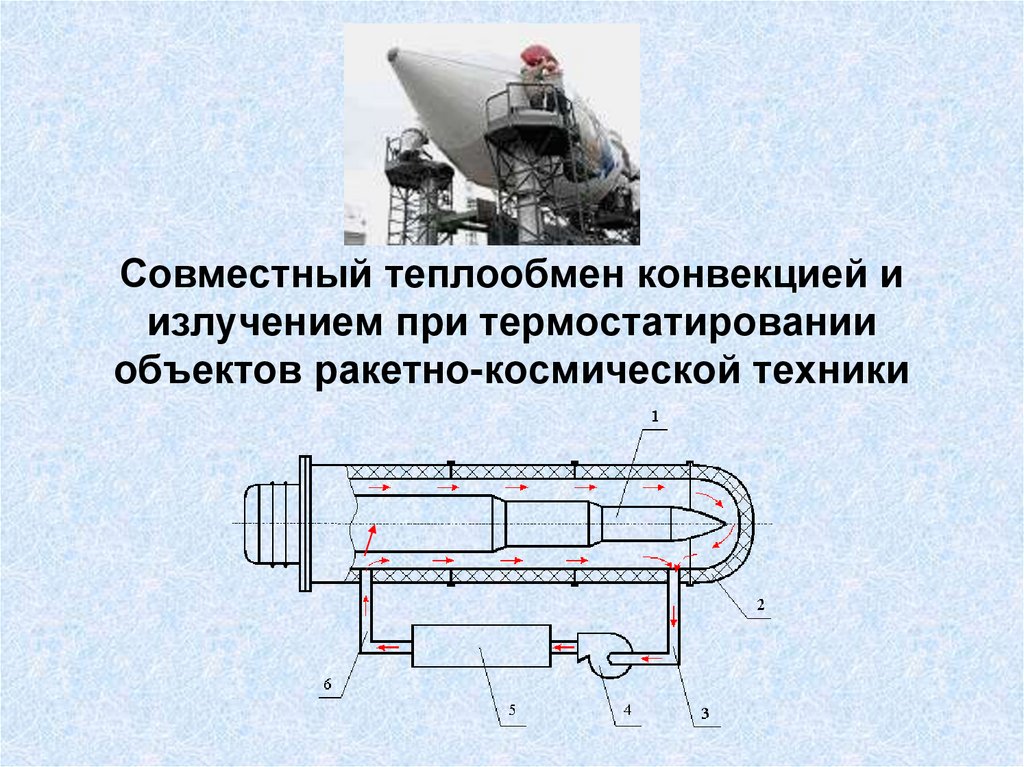







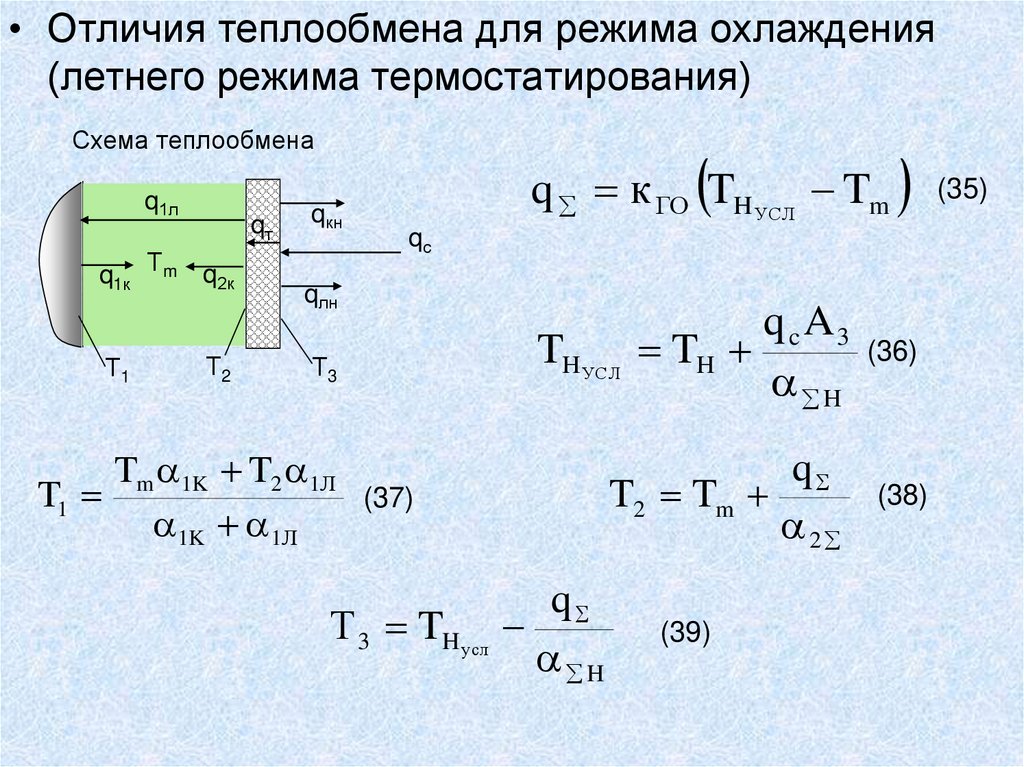
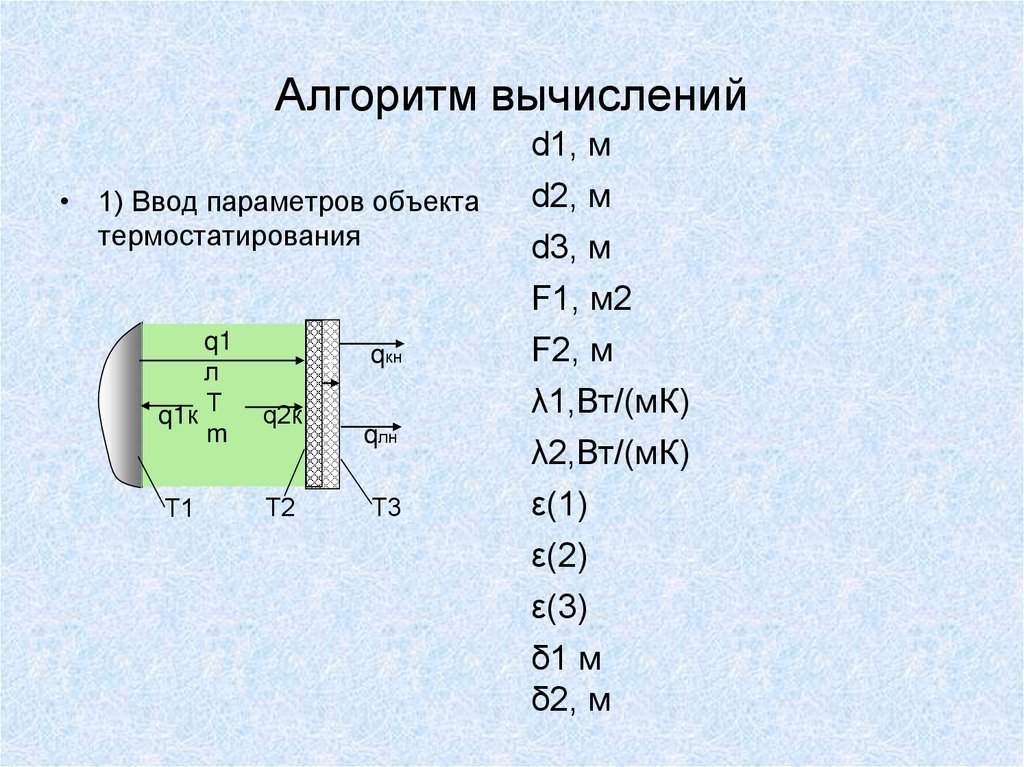


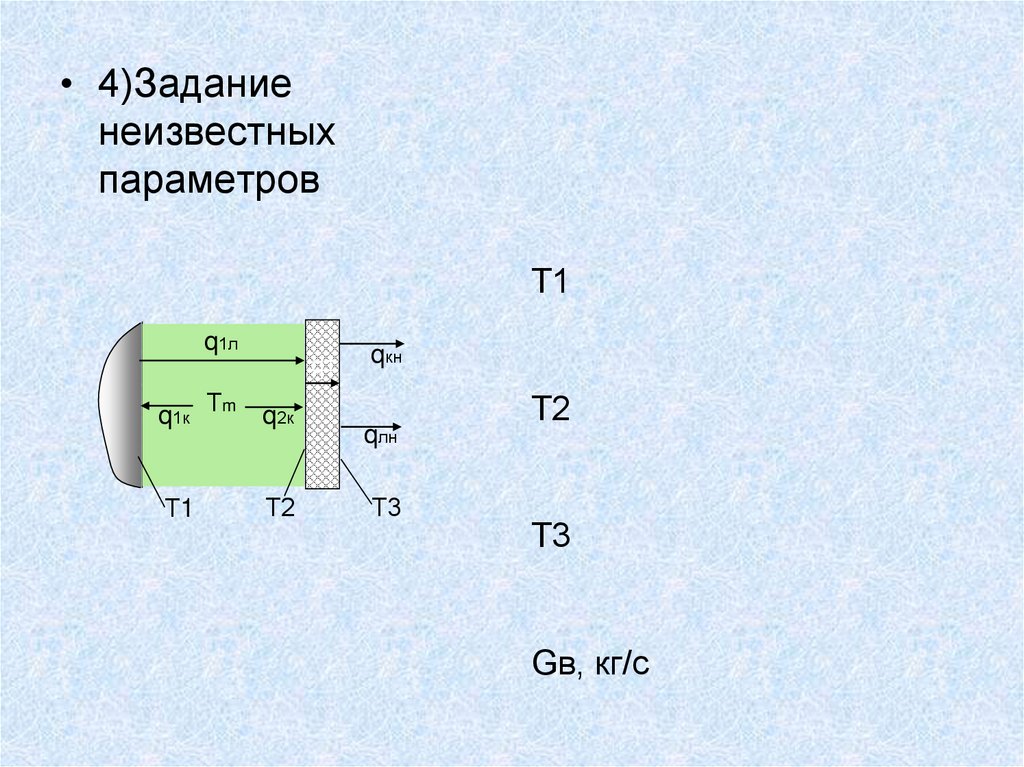



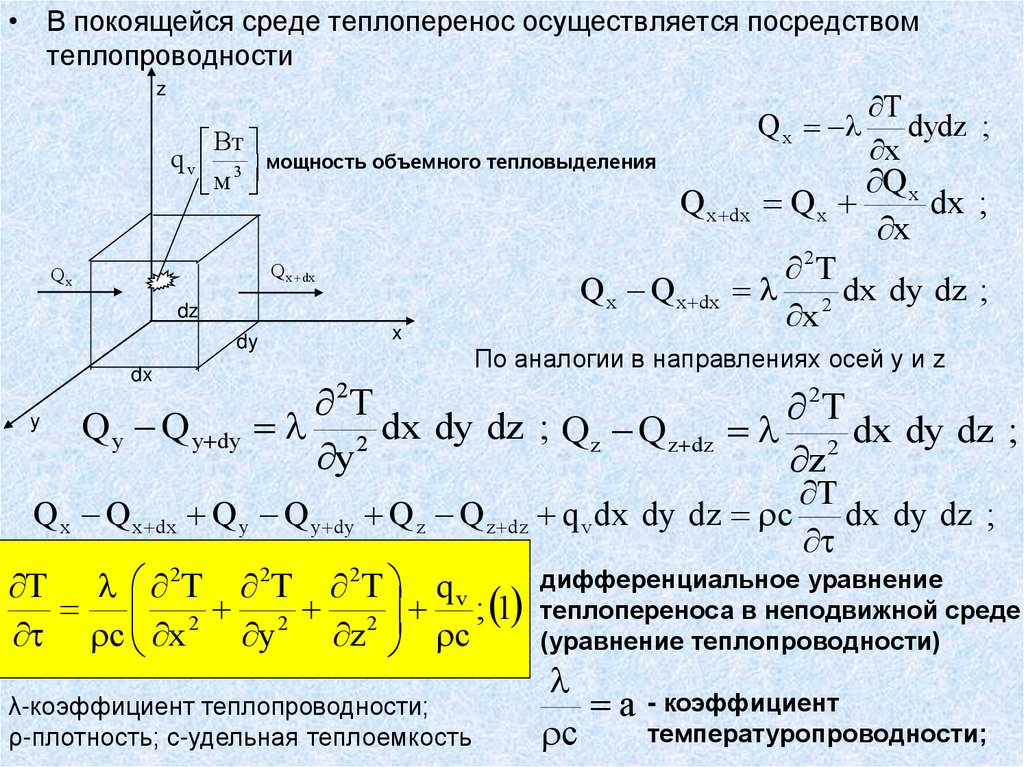



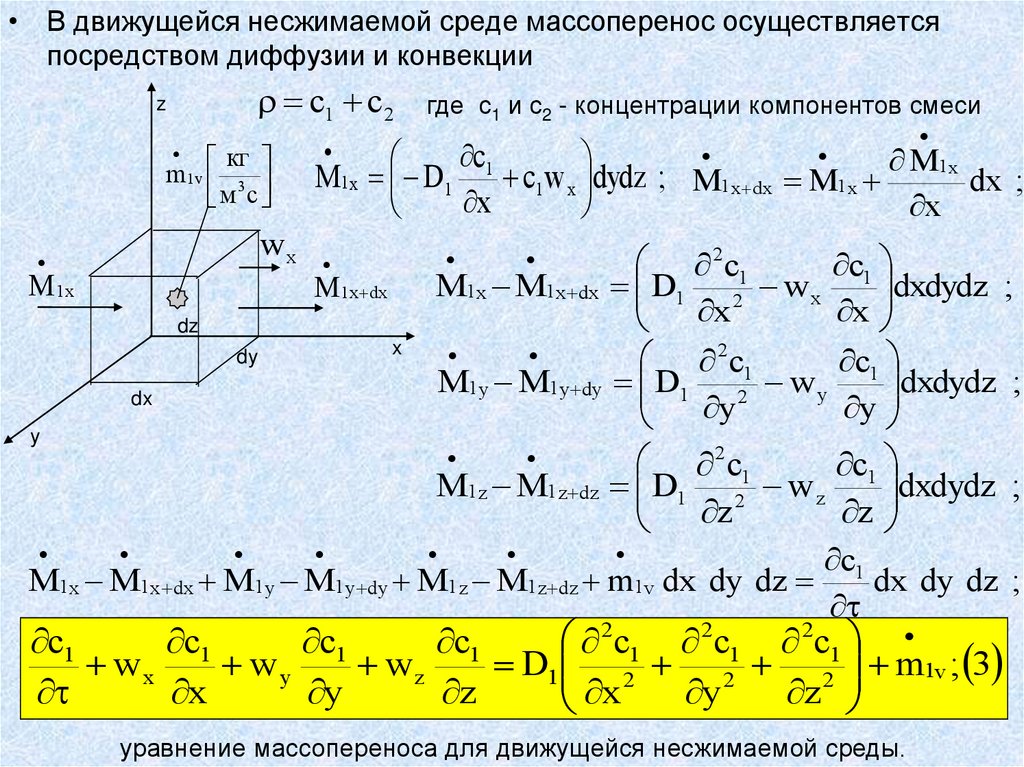










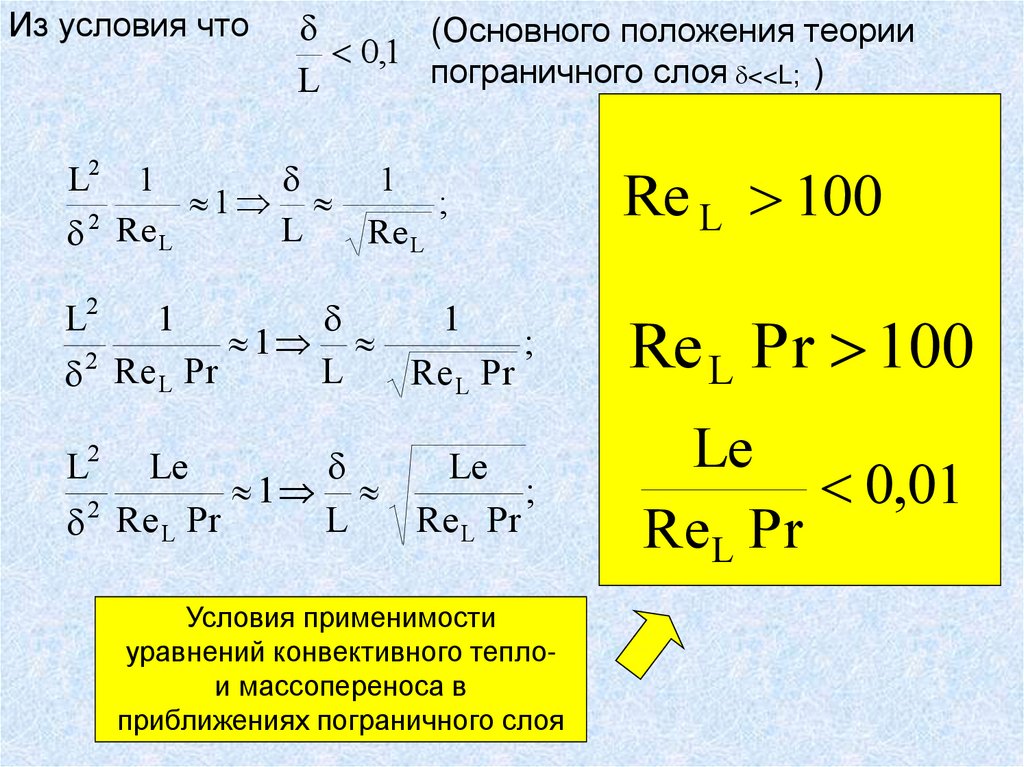










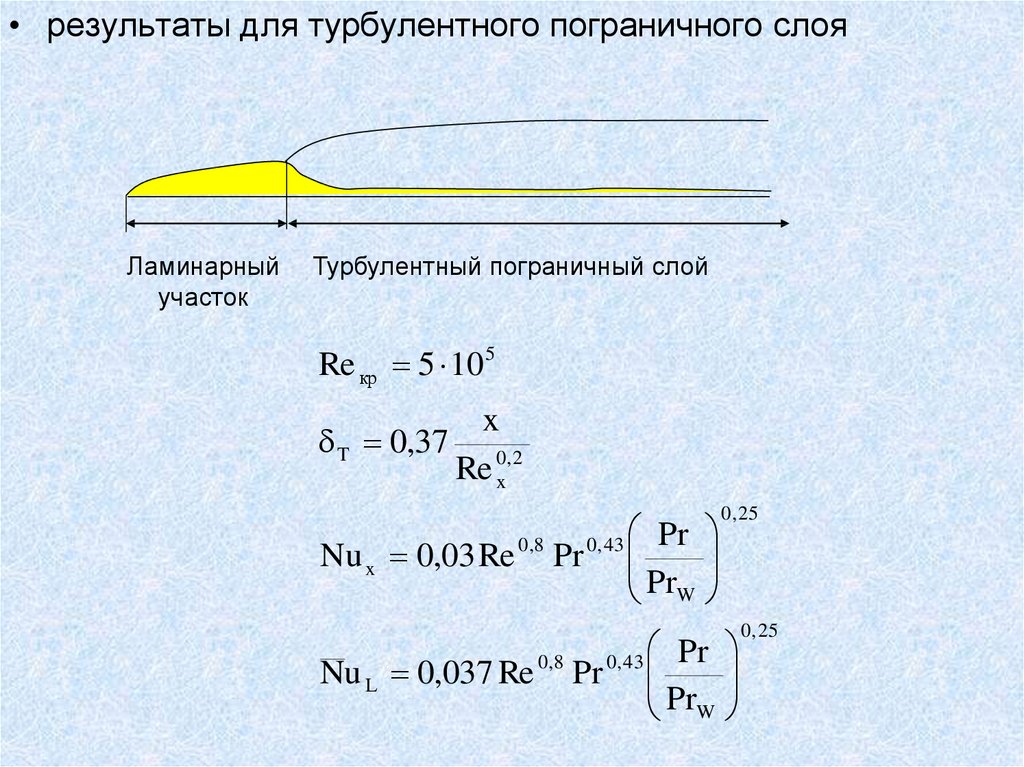
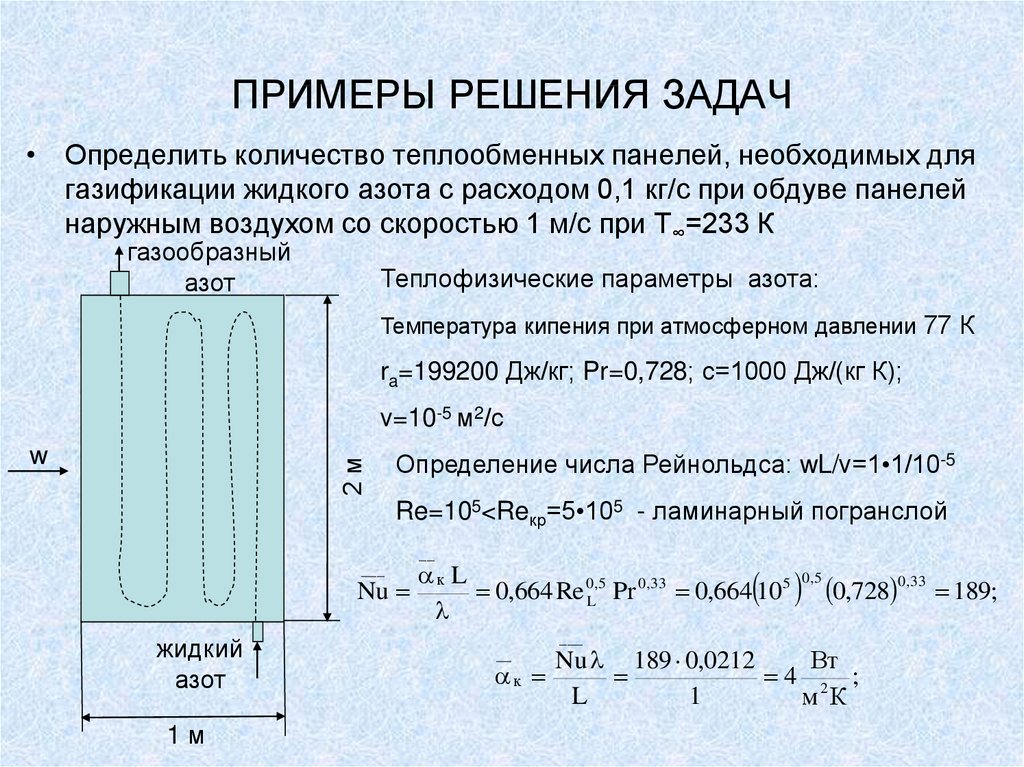



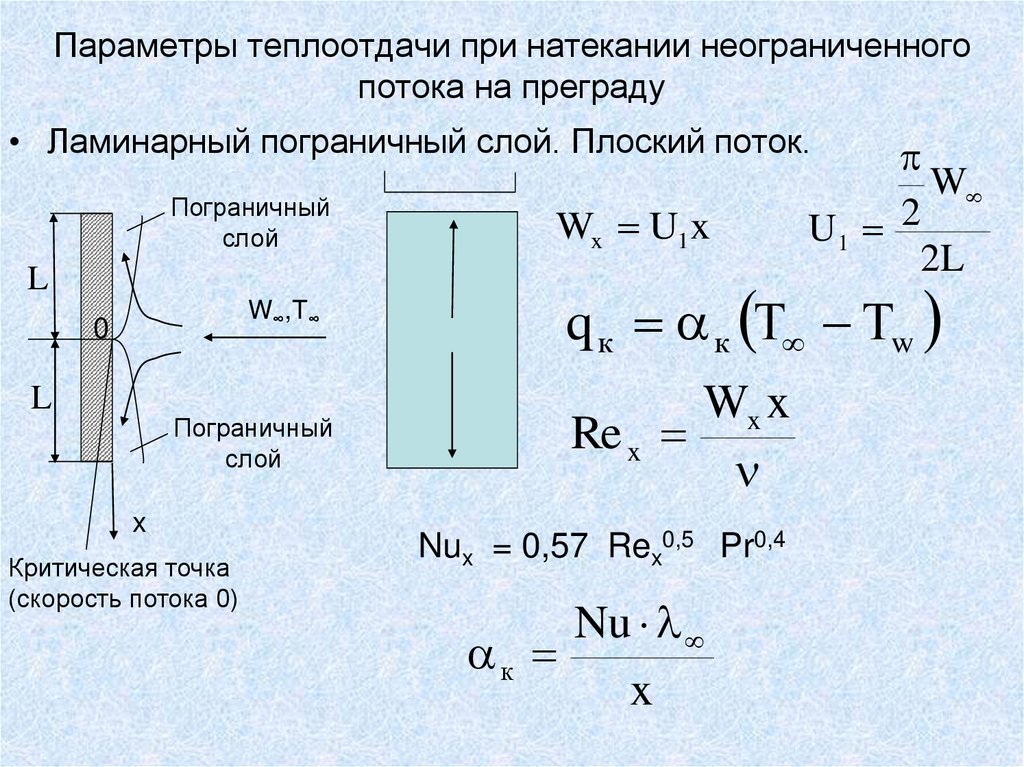
















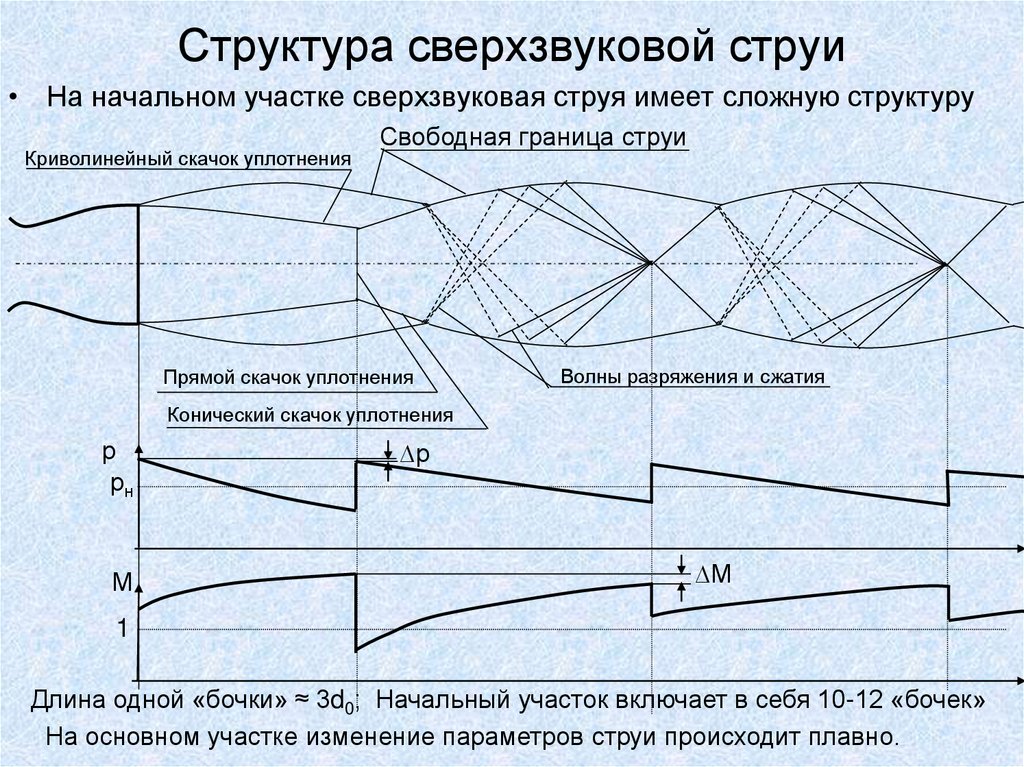






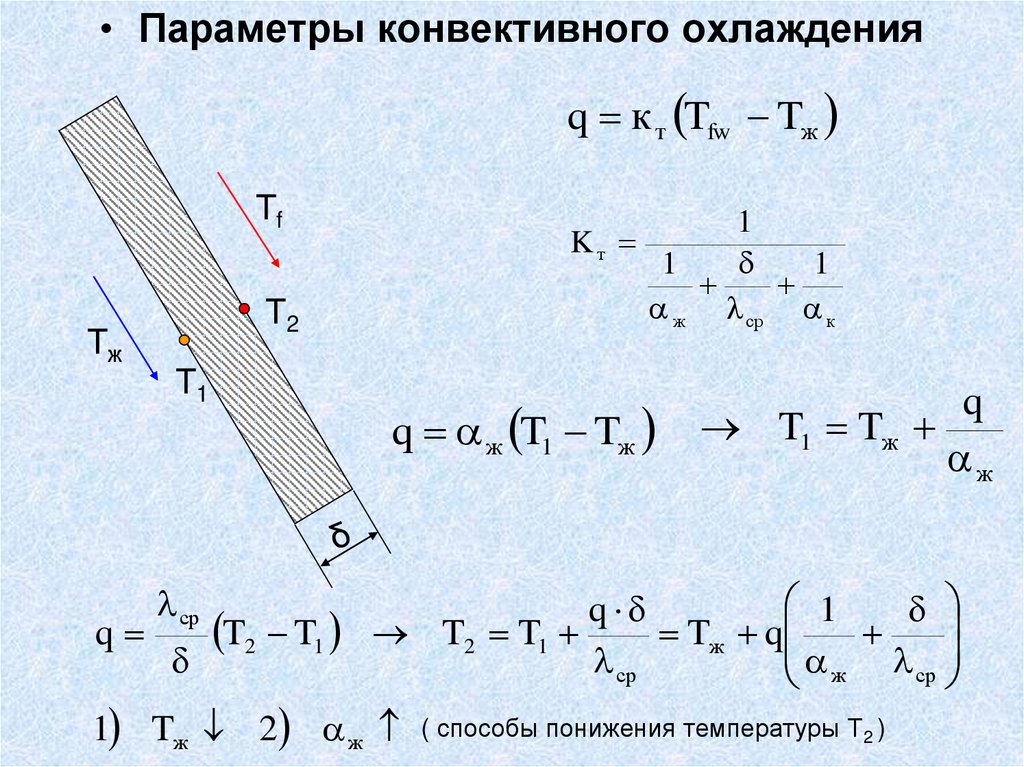
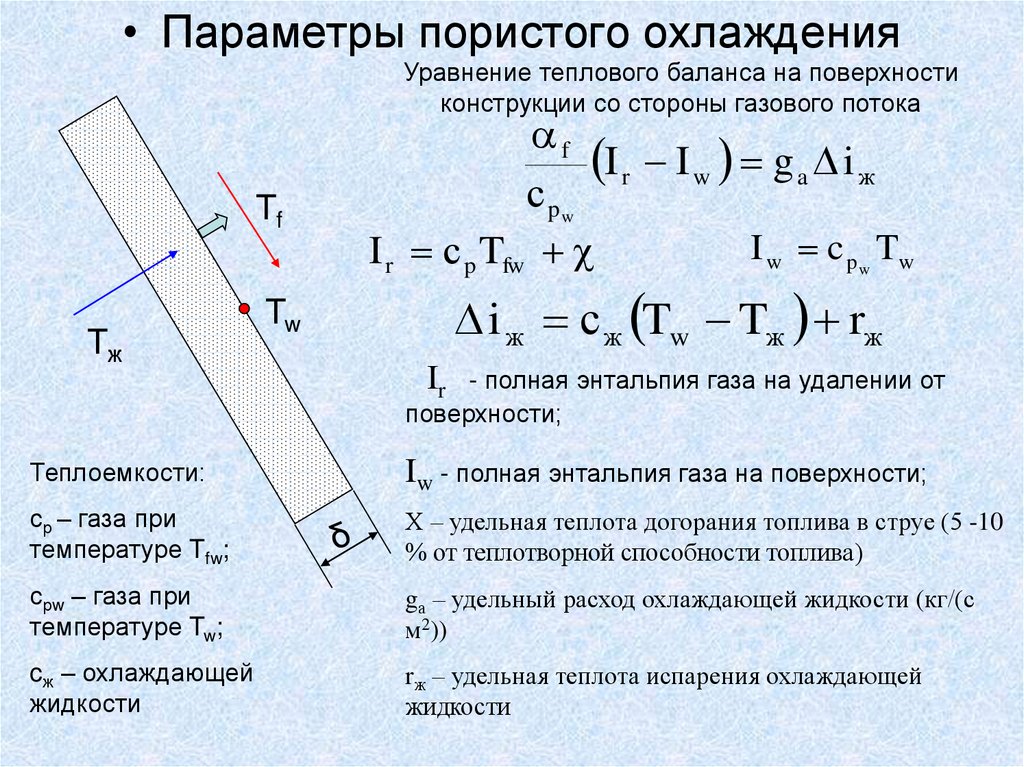





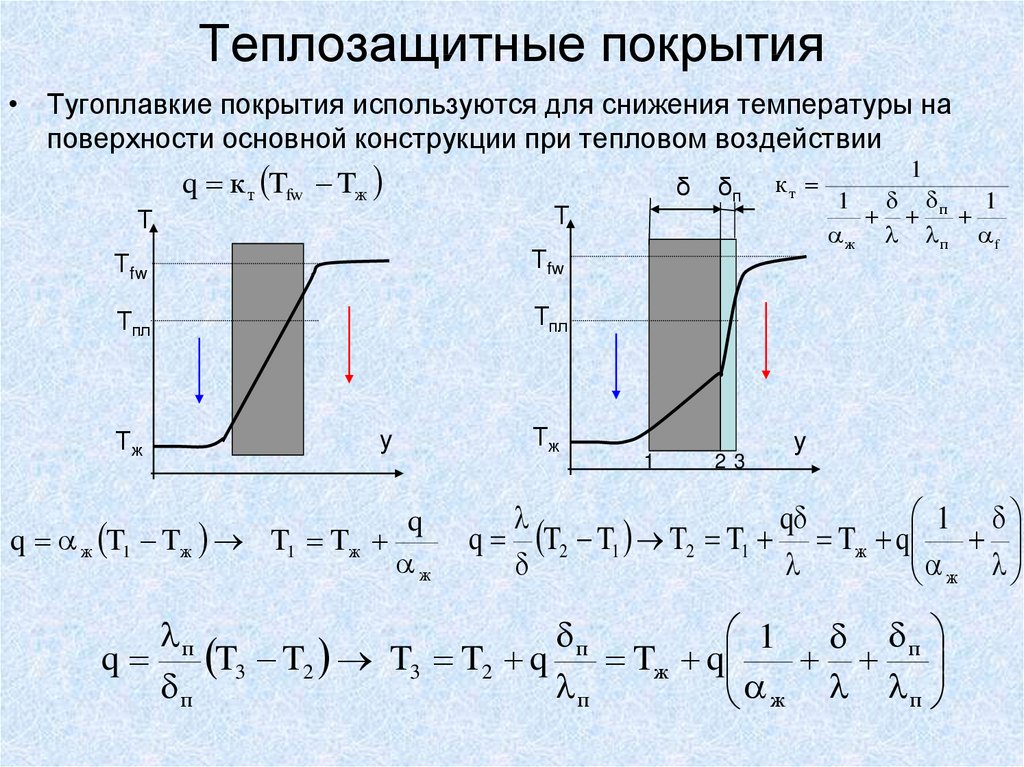

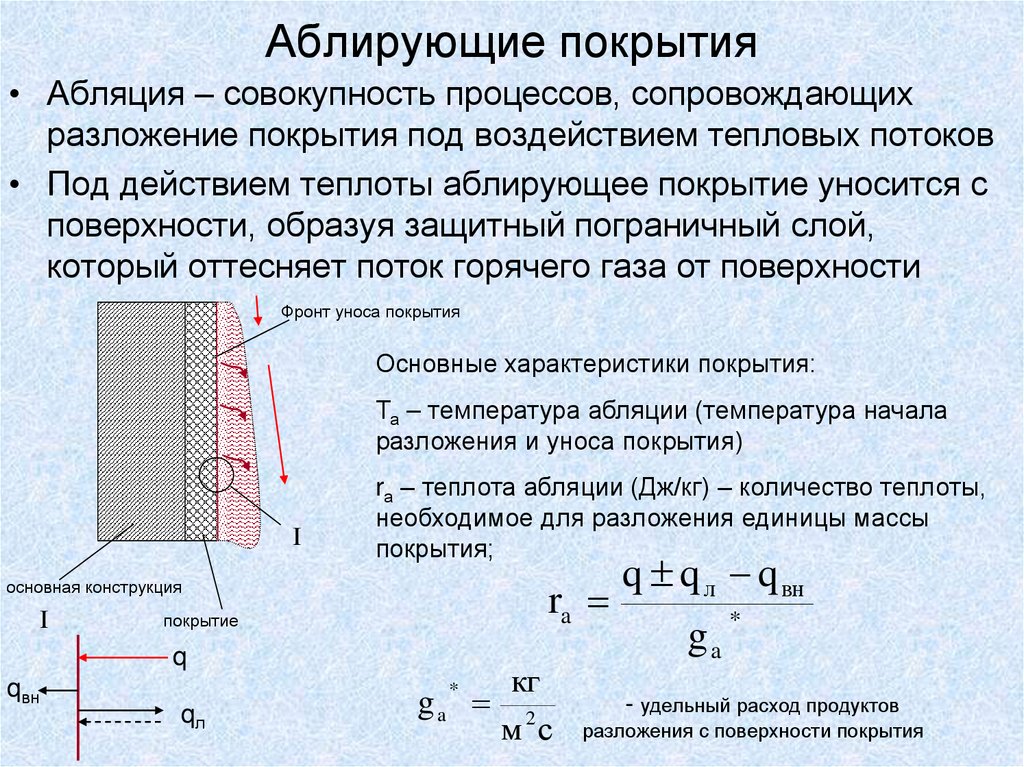


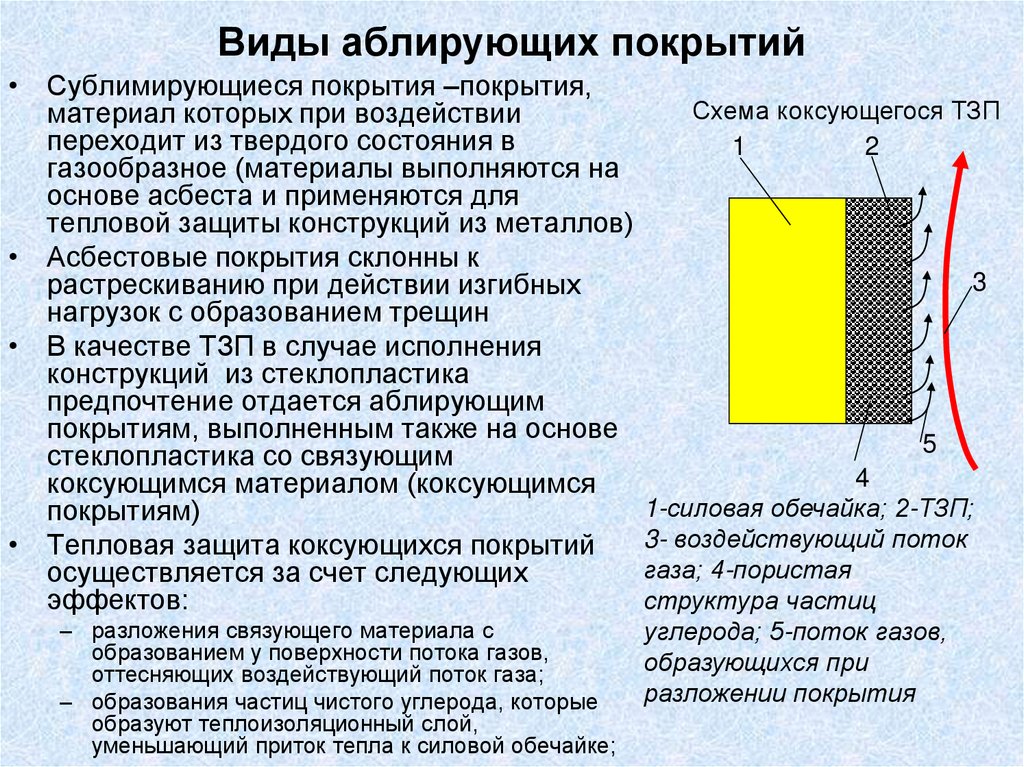




 physics
physics








