Определение остойчивости

1.

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Что такое
ОСТОЙЧИВОСТЬ
?
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
1

2.

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Так корабли строят дилетанты
Профессионалы спроектировали и и построили
«ТИТАНИК»
Изучайте ТЕОРИЮ КОРАБЛЯ
профессионально!
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
2

3. Что такое остойчивость?

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Что такое остойчивость?
• Остойчивость – это способность
судна противостоять внешним силам
и моментам без аварийных
последствий
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
3

4. Для удобства изучения остойчивость подразделяется на:

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Для удобства изучения остойчивость
подразделяется на:
• Поперечную, продольную и
вертикальную
• Статическую и динамическую
• Начальную и на больших углах крена
• Остойчивость неповреждённого и
аварийного судна
• Остойчивость на тихой воде и на
волнении и т.д.
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
4

5. Водоизмещение

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Водоизмещение
• Напомним, что термин «водоизмещение» в
равной степени относится как к вытесненной
воде, так и к судну.
• Массовое водоизмещение M – это и масса всех
конструкций и грузов судна и равная ей масса
вытесненной судном воды.
• Весовое водоизмещение D – это и вес всех
конструкций и грузов судна и вес вытесненной им
воды.
• Объёмное водоизмещение V – это и объём
подводной части судна и объём вытесненной им
воды.
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
5

6. Водоизмещение

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Водоизмещение
• Водоизмещение может быть измерено тремя
способами:
• в объемных единицах - тогда это объемное
водоизмещение V, м3;
• в весовых единицах - тогда это весовое
водоизмещение D, кН;
• в массовых единицах - тогда это массовое
водоизмещение М, т.
• Все это в принятой сейчас международной
системе единиц СИ. А есть и другие единицы
измерения….
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
6

7. Водоизмещение

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Водоизмещение
• Между этими водоизмещениями существует связь:
• V = D/g = M/r
• D = gV = gM
• М = rV = D/g
• где g-удельный вес воды;
для морской воды
g= 10.05 кН/м3;
r-плотность воды;
r= 1.025 т/м3;
• g- ускорение
свободного падения;
g = 9.81 м/с2.
• Кроме того, g =rg
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
7

8. Чем можно «измерить» остойчивость при равнообъёмных наклонениях?

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Чем можно «измерить» остойчивость при
равнообъёмных наклонениях?
M0
• Остойчивость измеряется
восстанавливающим
моментом, который
образуется силами веса D и
поддержания gV
• Mq=
=D lq [кН м]
• GZ= lq=yccosq +zcsinq -asinq
D.GZ
Цуренко Ю.И.
h0
a
q
Z
G
D
C
C0
gV
Теория корабля/ Ship Propulsion
8

9. Диаграмма статической остойчивости (ДСО)

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
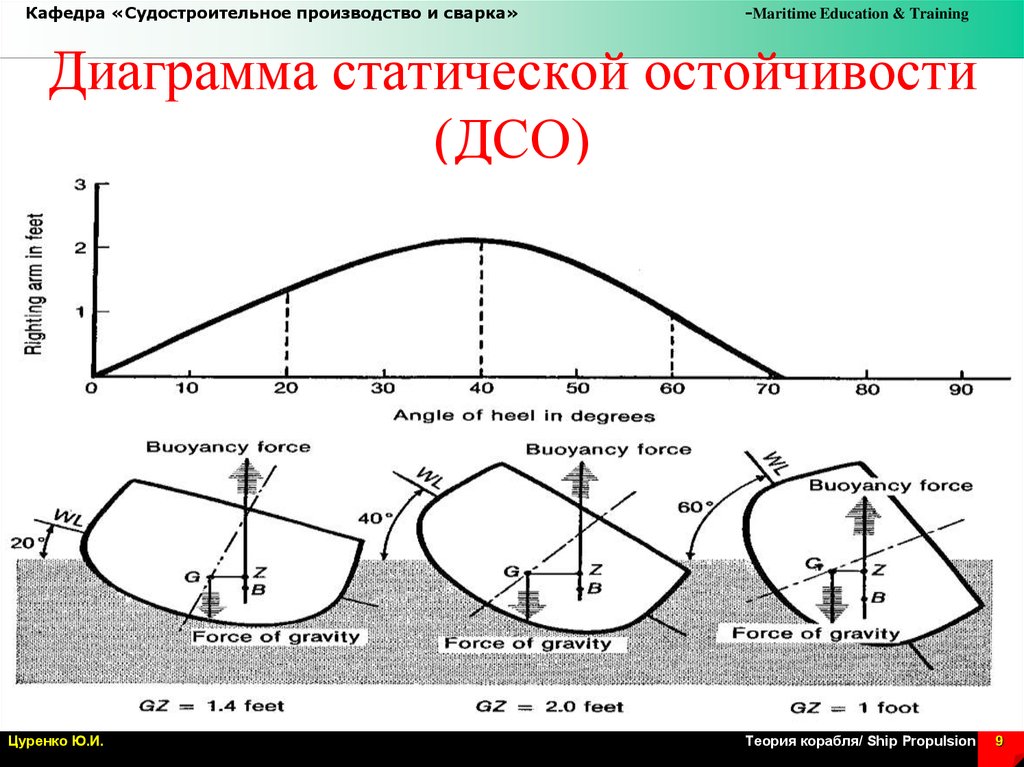
Диаграмма статической остойчивости
(ДСО)
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
9

10. ДСО в «моментах» и в «плечах»

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
ДСО в «моментах» и в «плечах»
• Так как
• lq= Mq /D = Dlq /D,
то
ДСО в «плечах» - это
восстанавливающий
момент, приходящийся
на единицу
водоизмещения
Mq
q
lq
q
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
10

11. ДСО в «моментах» и в «плечах»

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
ДСО в «моментах» и в «плечах»
• Вот почему восстанавливающие моменты у
различных по размерам судов отличаются в
десятки и сотни раз, а диаграммы
остойчивости в «плечах» - очень близки.
• Для понимания процессов удобнее
рассматривать ДСО в «моментах», а для
вычисления – в «плечах».
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
11

12. Кривые С, М, прометацентры

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
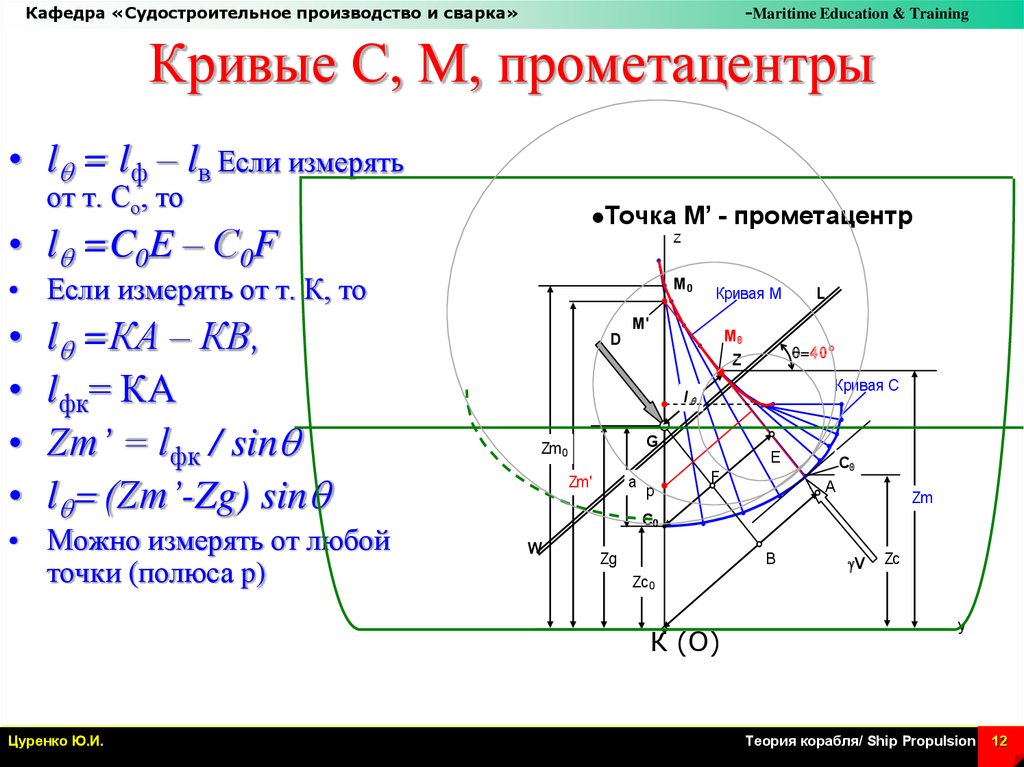
Кривые С, М, прометацентры
• lq = lф – lв Если измерять
от т. Со, то
Точка
• lq =C0E – С0F
z
• Если измерять от т. К, то
lq =КА – КВ,
lфк= КА
Zm’ = lфк / sinq
lq= (Zm’-Zg) sinq
• Можно измерять от любой
точки (полюса p)
M’ - прометацентр
M0
D
Кривая М
M'
Mq
Кривая С
lq
G
Zm'
a
p
E
F
Cq
A
Zm
C0
W
Zg
B
gV
Zc
Zc 0
К (О)
Цуренко Ю.И.
q=4 0 o
Z
Zm0
L
y
Теория корабля/ Ship Propulsion
12

13. Плечи остойчивости формы «от киля» и возвышения прометацентра

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
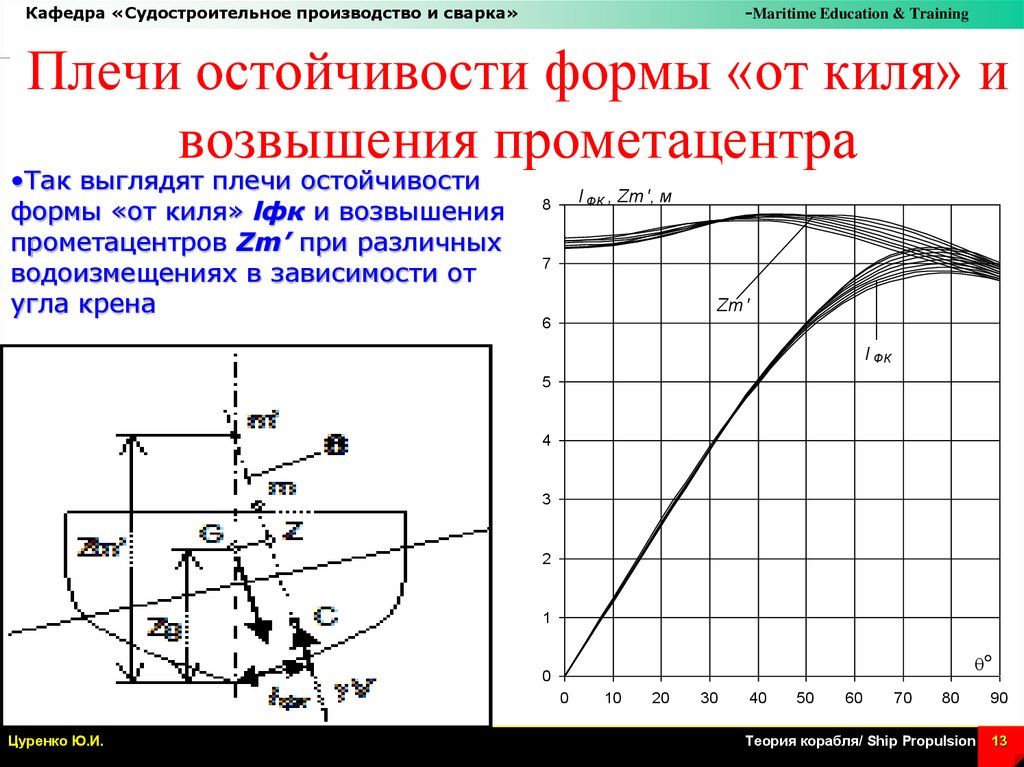
Плечи остойчивости формы «от киля» и
возвышения прометацентра
•Так выглядят плечи остойчивости
формы «от киля» lфк и возвышения
прометацентров Zm’ при различных
водоизмещениях в зависимости от
угла крена
l ФК , Zm', м
8
7
Zm'
6
l ФК
5
4
3
2
1
qo
0
0
Цуренко Ю.И.
10
20
30
40
50
60
70
80
Теория корабля/ Ship Propulsion
90
13

14. Пантокарены и прометацентры

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
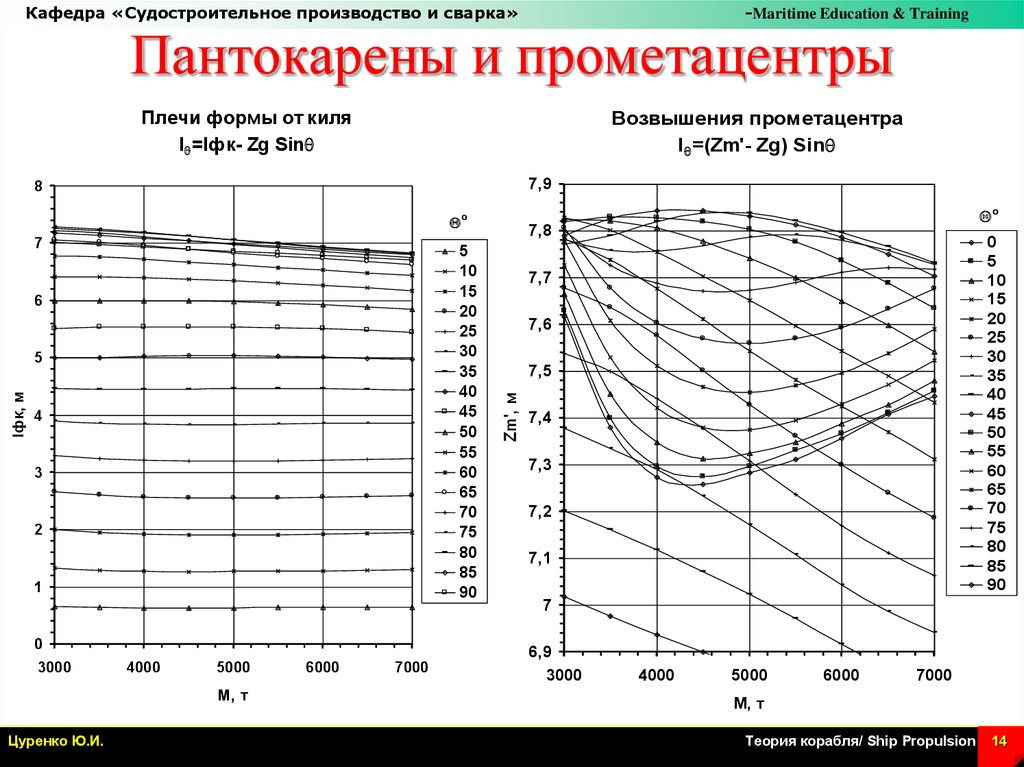
Пантокарены и прометацентры
Плечи формы от киля
lq =lфк- Zg Sinq
Возвышения прометацентра
lq =(Zm'- Zg) Sinq
7,9
8
7
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
6
lфк, м
5
4
3
2
1
0
3000
4000
5000
М, т
Цуренко Ю.И.
o
6000
7000
o
7,8
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
7,7
7,6
7,5
Zm', м
7,4
7,3
7,2
7,1
7
6,9
3000
4000
5000
6000
7000
М, т
Теория корабля/ Ship Propulsion
14

15. Метацентрические формулы остойчивости, малые углы крена

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
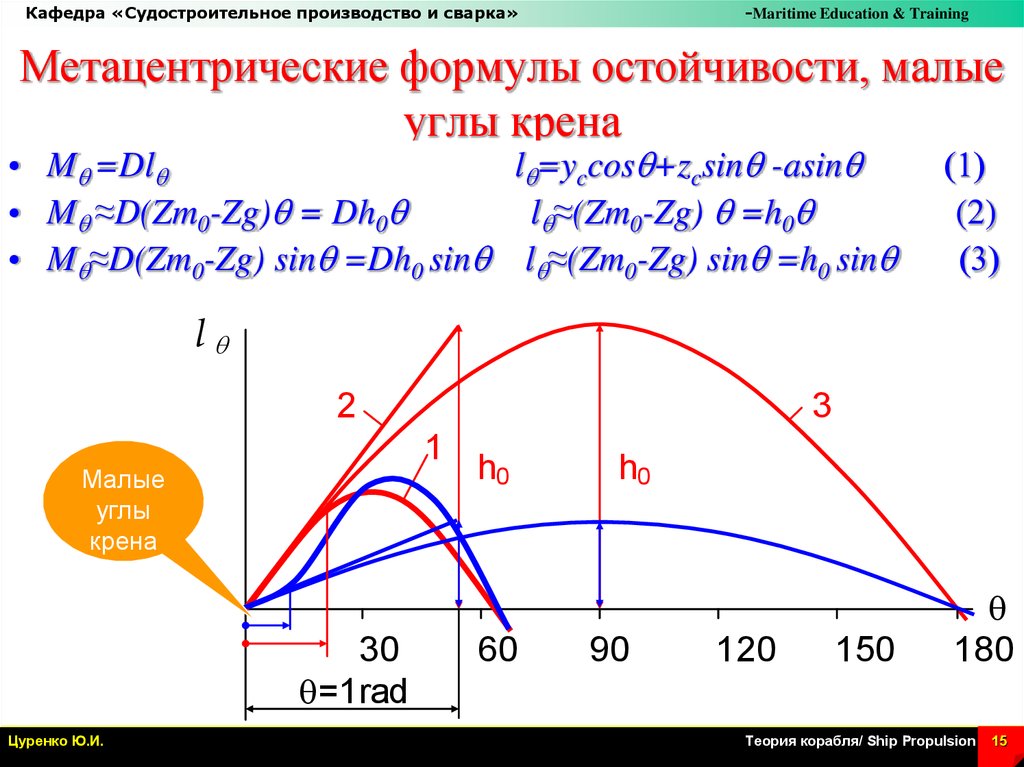
Метацентрические формулы остойчивости, малые
углы крена
• Mq =Dlq
lq=yccosq+zcsinq -asinq
• Mq ≈D(Zm0-Zg)q = Dh0q
lq≈(Zm0-Zg) q =h0q
• Mq≈D(Zm0-Zg) sinq =Dh0 sinq lq≈(Zm0-Zg) sinq =h0 sinq
(1)
(2)
(3)
lq
2
1
Малые
углы
крена
30
q=1rad
Цуренко Ю.И.
3
h0
60
h0
90
120
150
q
180
Теория корабля/ Ship Propulsion
15

16. Малые углы крена

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Малые углы крена
• Малые углы крена
это такие углы, при
которых метацентр
М0 практически не
выходит из ДП, а
дуга, описанная
метацентрическим
радиусом r0 ,
практически
совпадает с истинной
кривой С0С
M0
h0
Z
r0
G
C0
r0 = Ix / V
D
q
C
gV
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
16

17. Чем измерить остойчивость при малых углах крена?

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Чем измерить остойчивость при
малых углах крена?
• Когда угол крена стремится к нулю,
восстанавливающий момент также стремится к нулю и
плохо характеризует остойчивость.
• Гораздо лучше её характеризует скорость изменения
момента.
• А это – угол наклона начального участка ДСО. Тангенс
этого угла определяется производной.
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
17

18. Коэффициент остойчивости и метацентрическая высота как мера остойчивости при малых углах крена

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
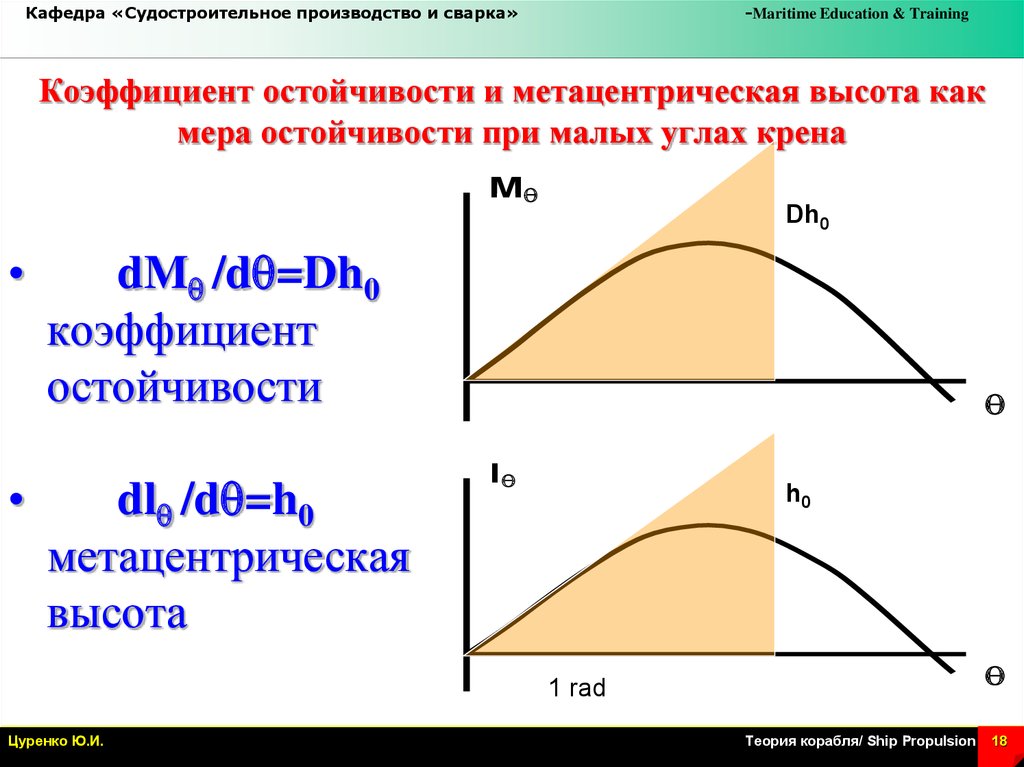
Коэффициент остойчивости и метацентрическая высота как
мера остойчивости при малых углах крена
Mq
Dh0
dMq /dq=Dh0
коэффициент
остойчивости
dlq /dq=h0
метацентрическая
высота
q
lq
h0
q
1 rad
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
18

19. Кренящий момент как функция угла крена

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
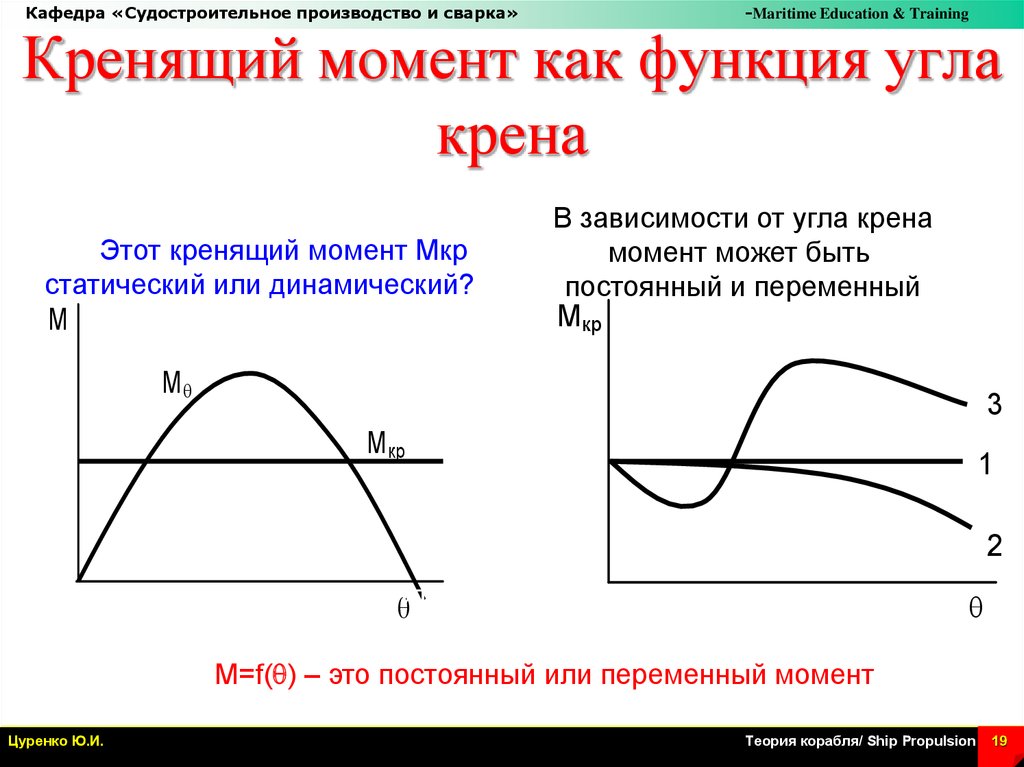
Кренящий момент как функция угла
крена
Этот кренящий момент Мкр
статический или динамический?
M
В зависимости от угла крена
момент может быть
постоянный и переменный
Мкр
Mq
3
Mкр
На этот вопрос
по данному графику ответить
q нельзя!
1
1 – постоянный
2, 3 - переменный
2
q
M=f(q) – это постоянный или переменный момент
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
19

20. Кренящий момент как функция времени

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
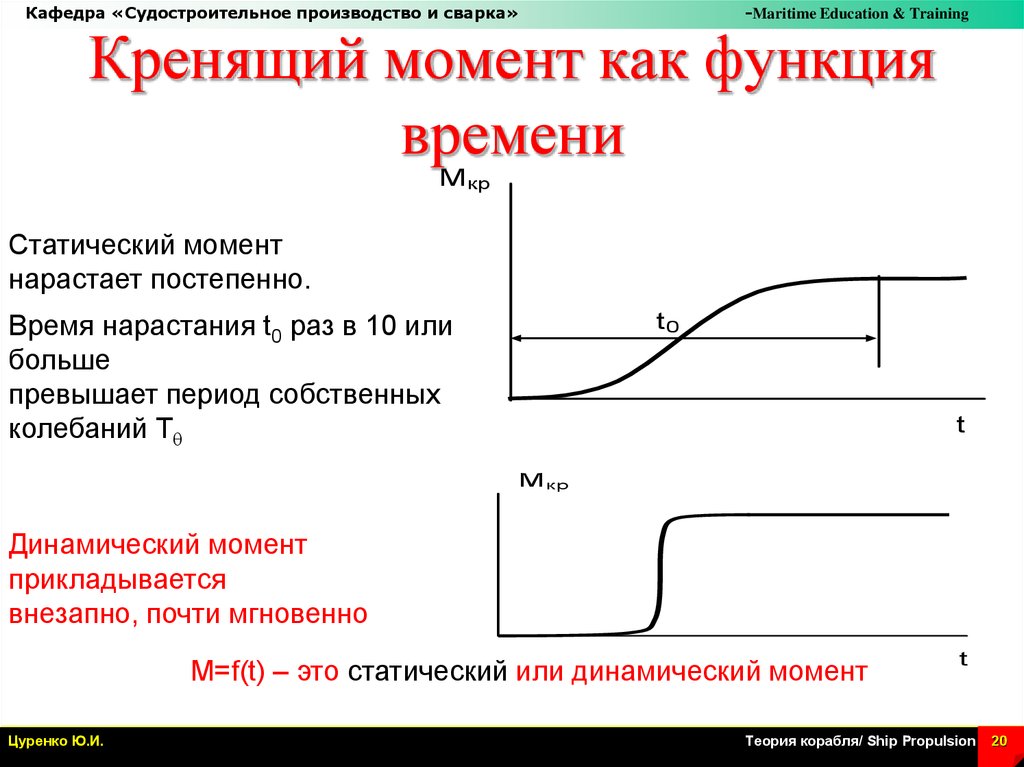
Кренящий момент как функция
времени
Мкр
Статический момент
нарастает постепенно.
t0
Время нарастания t0 раз в 10 или
больше
превышает период собственных
колебаний Тq
t
Мкр
Динамический момент
прикладывается
внезапно, почти мгновенно
M=f(t) – это статический или динамический момент
Цуренко Ю.И.
t
Теория корабля/ Ship Propulsion
20

21. Крен судна под действием статически и динамически приложенного кренящего момента на тихой воде

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
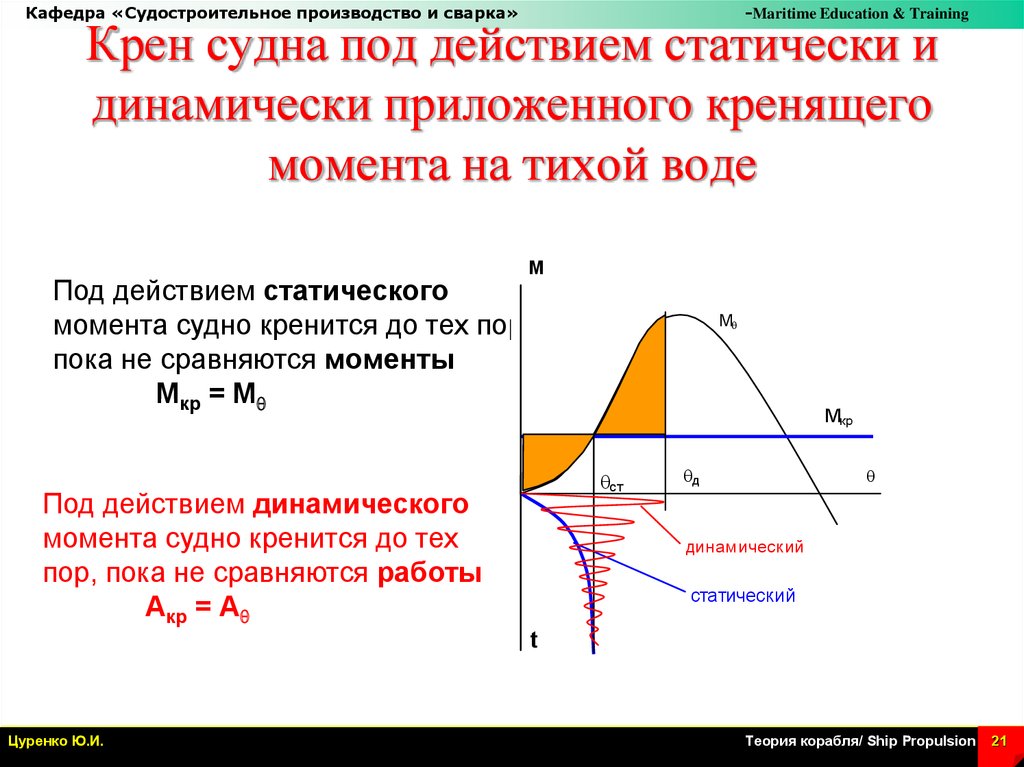
Крен судна под действием статически и
динамически приложенного кренящего
момента на тихой воде
M
Под действием статического
момента судно кренится до тех пор,
пока не cравняются моменты
Мкр = Мq
Мq
Mкр
qст
Под действием динамического
момента судно кренится до тех
пор, пока не сравняются работы
Акр = Аq
qд
q
динамический
статический
t
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
21

22. Опрокидывание судна на тихой воде под действием статически приложенного кренящего момента

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
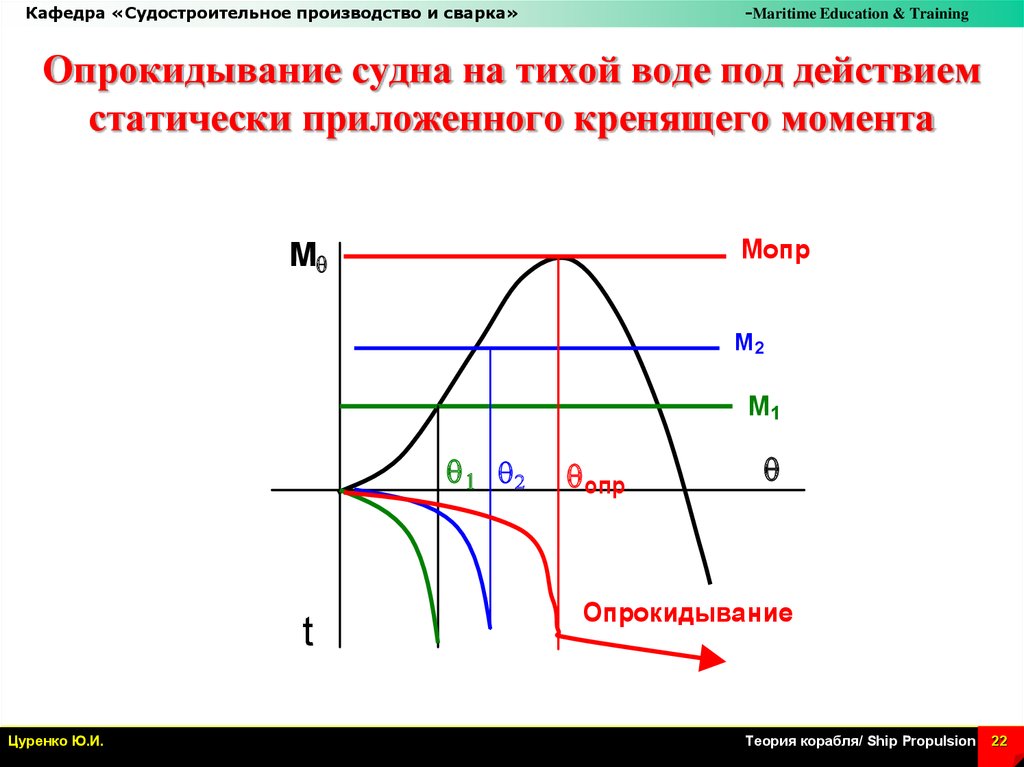
Опрокидывание судна на тихой воде под действием
статически приложенного кренящего момента
Мопр
Мq
М2
М1
q1 q2
t
Цуренко Ю.И.
q опр
q
Опрокидывание
Теория корабля/ Ship Propulsion
22

23. Опрокидывание высокобортных судов на тихой воде под действием динамически приложенного кренящего момента

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
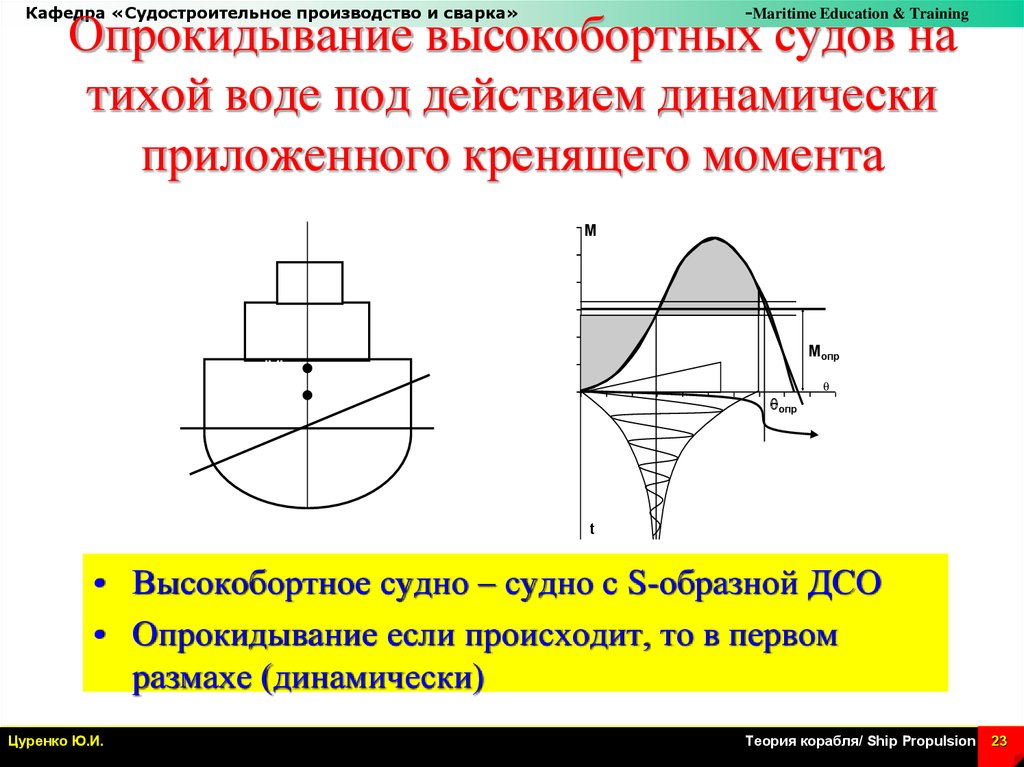
Опрокидывание высокобортных судов на
тихой воде под действием динамически
приложенного кренящего момента
M
М опр
Mo
q
q опр
G
t
• Высокобортное судно – судно с S-образной ДСО
• Опрокидывание если происходит, то в первом
размахе (динамически)
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
23

24. Опрокидывание низкобортных судов на тихой воде под действием динамически приложенного кренящего момента

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Опрокидывание низкобортных судов на тихой
воде под действием динамически
приложенного кренящего момента
M
Mo
Mq
Mопр
G
q опр
q
t
• Низкобортное судно – это обычно судно с выпуклой ДСО
• При первом накренении, когда в воду входит палуба и
фальшборт, резко увеличивается сила демпфирования и
процесс накренения существенно замедляется
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
24

25. Опрокидывание низкобортных судов на тихой воде под действием динамически приложенного кренящего момента

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Опрокидывание низкобортных судов на тихой
воде под действием динамически
приложенного кренящего момента
• Судно совершает затухающие колебания вокруг
постепенно возрастающего «псевдостатического»
угла крена
• Если крен достигает угла максимума диаграммы
статической остойчивости, то судно
опрокидывается. Это происходит практически
«в статике»
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
25

26. Что такое потеря остойчивости ?

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Что такое потеря остойчивости ?
• Потеря остойчивости означает переход к такому режиму
движения, который практически недопустим. При этом судно
начнёт совершать колебания относительно второго
устойчивого положения равновесия – вверх килём
lq
q
0
90
180
270
360
t
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
26

27. Благодарю за внимание

Кафедра «Судостроительное производство и сварка»
-Maritime Education & Training
Благодарю за внимание
Цуренко Ю.И.
Теория корабля/ Ship Propulsion
27