Similar presentations:
Сети Петри
1. Сети Петри
• Сеть Петри определяется как четверка <Р, Т, I, O>, где Р и Т конечные множества позиций и переходов, I и O - множествавходных и выходных функций.
• В сетях Петри вводятся объекты двух типов: динамические, которые
изображаются метками (маркерами) внутри позиций, и
статические, которые соответствуют вершинам сети Петри.
• Маркировка - распределение маркеров по позициям. Маркеры
могут перемещаться в сети. Каждое изменение маркировки
называют событием, причем каждое событие связано с
определенным переходом. События происходят мгновенно и
разновременно при выполнении некоторых условий.
• Каждому условию в сети Петри соответствует определенная
позиция. Совершению события соответствует срабатывание
перехода, при котором маркеры из входных позиций этого перехода
перемещаются в выходные позиции. Последовательность событий
образует моделируемый процесс.
2. ОСНОВЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ СЛОЖНЫХ ДИНАМИЧЕСКИХ СИСТЕМ
• Правила срабатывания переходов конкретизируют следующимобразом: переход срабатывает, если для каждой из его входных
позиций выполняется условие Ni >= Ki, где Ni - число маркеров в iй входной позиции, Ki - число дуг, идущих от i-й позиции к
переходу; при срабатывании перехода число маркеров в i-й
входной позиции уменьшается на Ki, а в j-й выходной позиции
увеличивается на Мj где Мj - число дуг, связывающих переход с j-й
позицией.
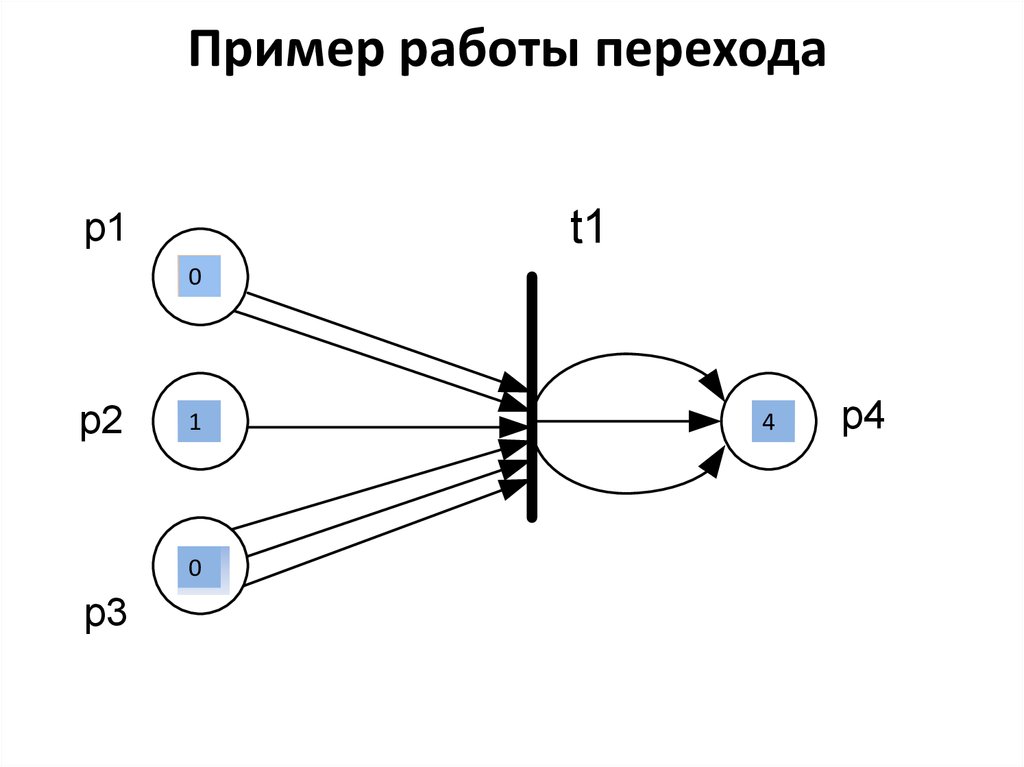
На рисунке показан пример распределения маркеров по
позициям. Для срабатывания перехода эту маркировку можно
записать в виде (2, 1, 3, 1) или (2 1 3 1). После срабатывания
перехода маркировка принимает вид (0,0,0,4).
3. Пример работы перехода
p1.
t1
1
0
2
p2
p3
..
2
1
.0.3
.
.41
p4
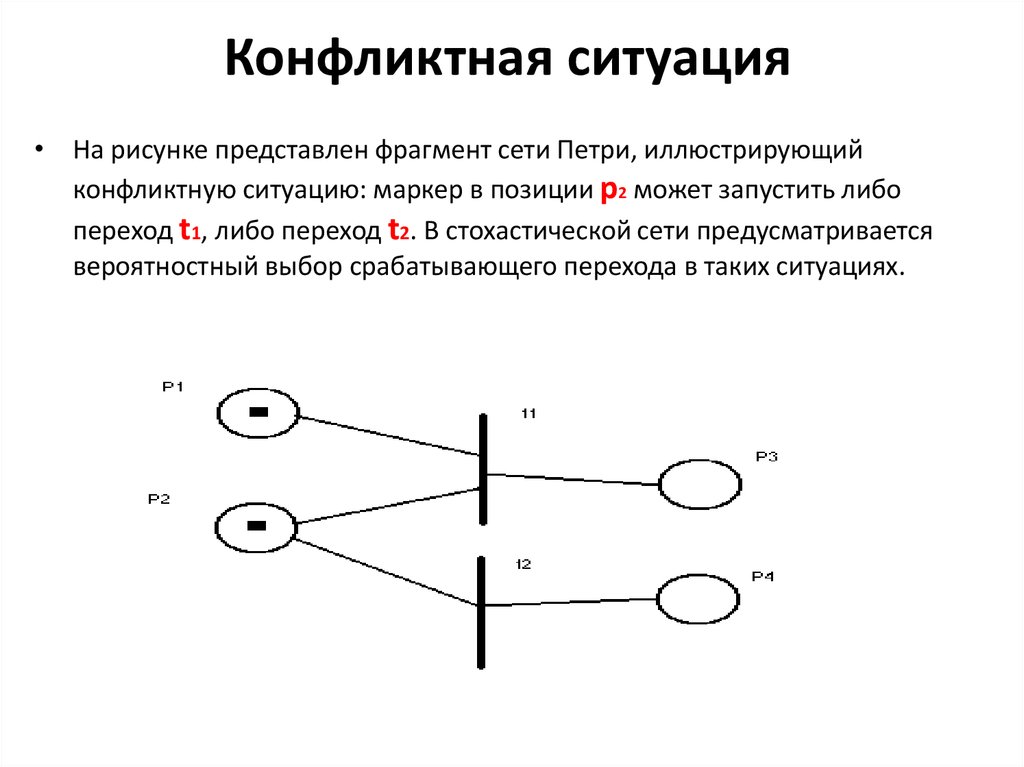
4. Конфликтная ситуация
• На рисунке представлен фрагмент сети Петри, иллюстрирующийконфликтную ситуацию: маркер в позиции р2 может запустить либо
переход t1, либо переход t2. В стохастической сети предусматривается
вероятностный выбор срабатывающего перехода в таких ситуациях.
5. Задание для моделирования
На заводе C производиться изделие из 1-гокомплектующего завода А и 2-х комплектующих завода В.
Потом, полученное изделие дорабатывается на заводе D с
использованием 1-го комплектующего завода Е и 1-го
комплектующего с завода В, причем, завод С имеет
возможность одновременной сборки 3-х изделий, а завод
D 2-х. Сборка на заводах возможна только при условии
готовности сборочных цехов. Изделие, собранное на
заводе D необходимо проверить на исправность.
Задание: построить сети Петри, провести анализ
достижимости, создать модель на основе двудольного
ориентированного графа.
www.sapr.favt.tsure.ru
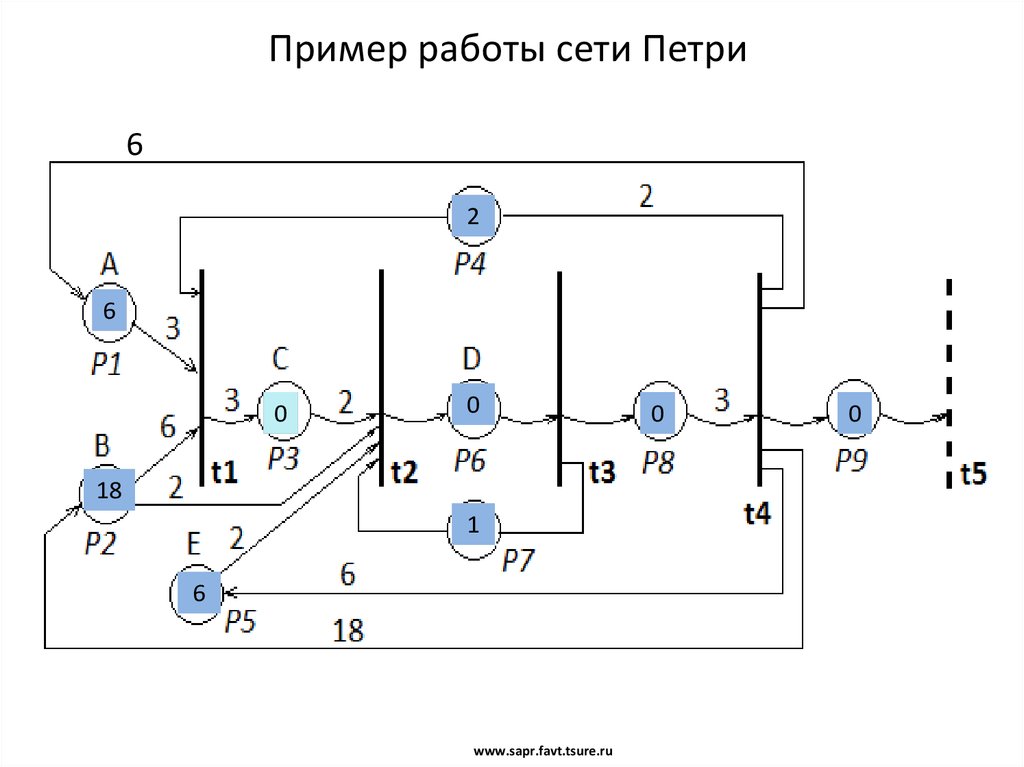
6. Пример работы сети Петри
61
0
2
36
0
30
6
4
2
0
1
12
18
60
2
4
0
1
4
2
0
6
www.sapr.favt.tsure.ru
1
2
0
3
1
0
7. Построение графа достижимости
6,18,0,2,6,0,1,0,0t1
t5
t4
3,12,3,1,6,0,1,0,0
0,0,0,0,0,0,1,3,0
t1
t3
0,6,6,0,6,0,1,0,0
0,0,0,0,0,1,0,2,0
t2
t2
0,4,4,0,4,1,0,0,0
t3
6,18,0,2,6,0,1,0,1
0,2,2,0,2,0,1,2,0
t2
0,4,4,0,4,0,1,1,0
t3
0,2,2,0,2,1,0,1,0
www.sapr.favt.tsure.ru
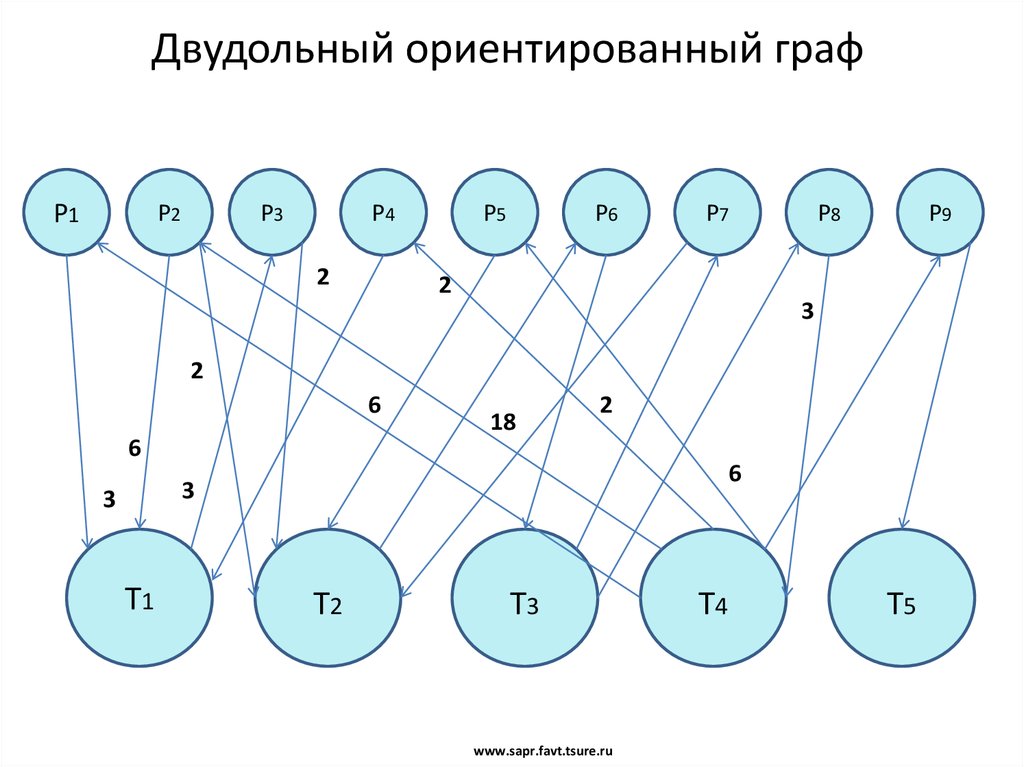
8. Двудольный ориентированный граф
P1P2
P3
P4
2
P5
P6
P7
2
P8
P9
3
2
6
6
18
2
6
3
3
T1
T2
T3
www.sapr.favt.tsure.ru
T4
T5




 programming
programming