Сети Петри

1. Сети Петри

Лекция 9

2. Дискретные динамические системы

Одним из наиболее общих понятий в
кибернетике и информатике является понятие
дискретной динамической системы
Дискретной динамической системой называется
система обладающая некоторым набором
состояний, переход между которыми
происходит в дискретные моменты времени
Примером дискретной динамической системы
является автомат

3. Детерминированные последовательные системы

Понятие конечного автомата существенно
связано с понятиями алгоритма и
последовательной алгоритмической системы
Поведение таких систем детерминировано: они
последовательно переходят из одного
состояния в другое в соответствии в
определенной функцией перехода
Конечные автоматы не подходят для описания
дискретных систем более общего вида –
недетерминированных параллельных систем

4. Недетерминированные параллельные системы

Подобные системы состоят из отдельных
компонентов, функционирующих параллельно
и взаимодействующих между собой асинхронно
(т.е. в произвольные моменты времени)
Примерами таких систем могут служить:
вычислительные системы, в том числе и
параллельные;
компьютерные сети и программные системы,
обеспечивающие их функционирование;
экономические системы;
системы управления дорожным движением и т. д.

5. Модели дискретных систем

При моделировании дискретных систем
действия их компонентов представляются
абстрактными событиями
Примеры событий:
выполнение оператора программы,
прерывание в операционной системе,
завершение технологической операции в
производственном процессе и т.д.
Событие может произойти один раз или
повторяться многократно; совокупность
событий в динамической системе, образует
процесс, порождаемый этой системой

6. Синхронные модели

В синхронных моделях события явно привязаны
к определенным моментам или интервалам
времени
Это приводит к необходимости учета состояния
всех компонентов системы при смене её общего
состояния
В синхронных моделях не заложена
информация о причинно-следственных связях
между событиями в системе
Они сложны для моделирования длительных
событий

7. Асинхронные модели

В моделях этого типа вышеперечисленные
проблемы отсутствуют
В асинхронных моделях временная связь
заменяется причинно-следственной
Отказ от времени позволяет считать события
или неделимыми («мгновенными»), или
составными, состоящими из «подсобытий»

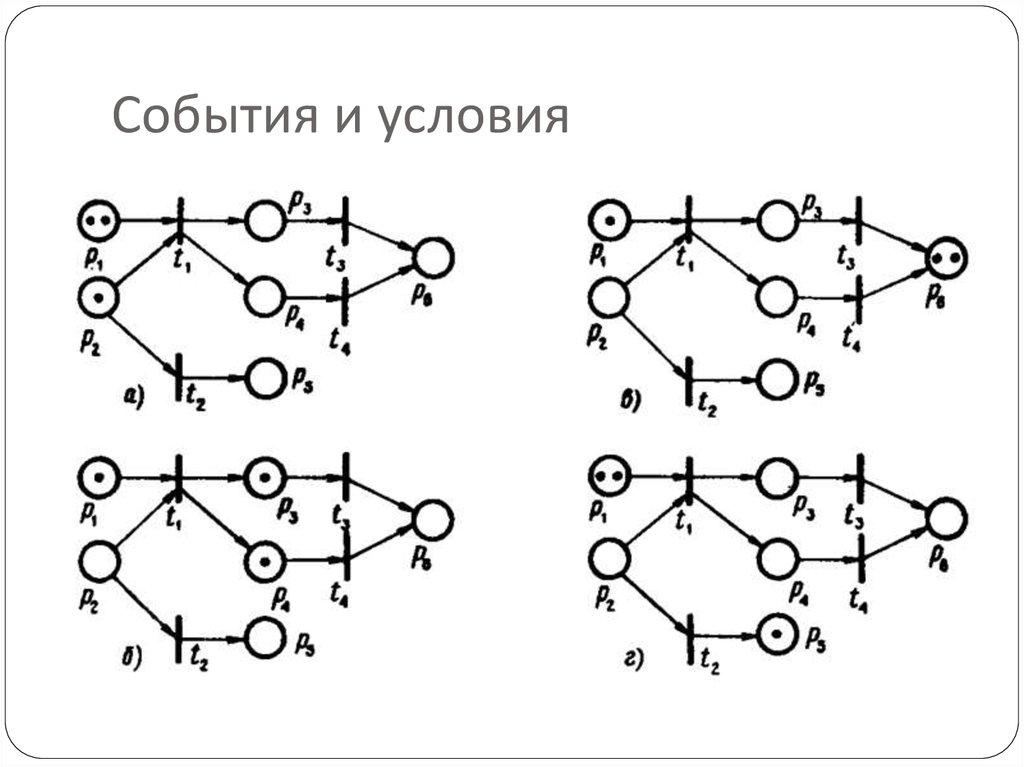
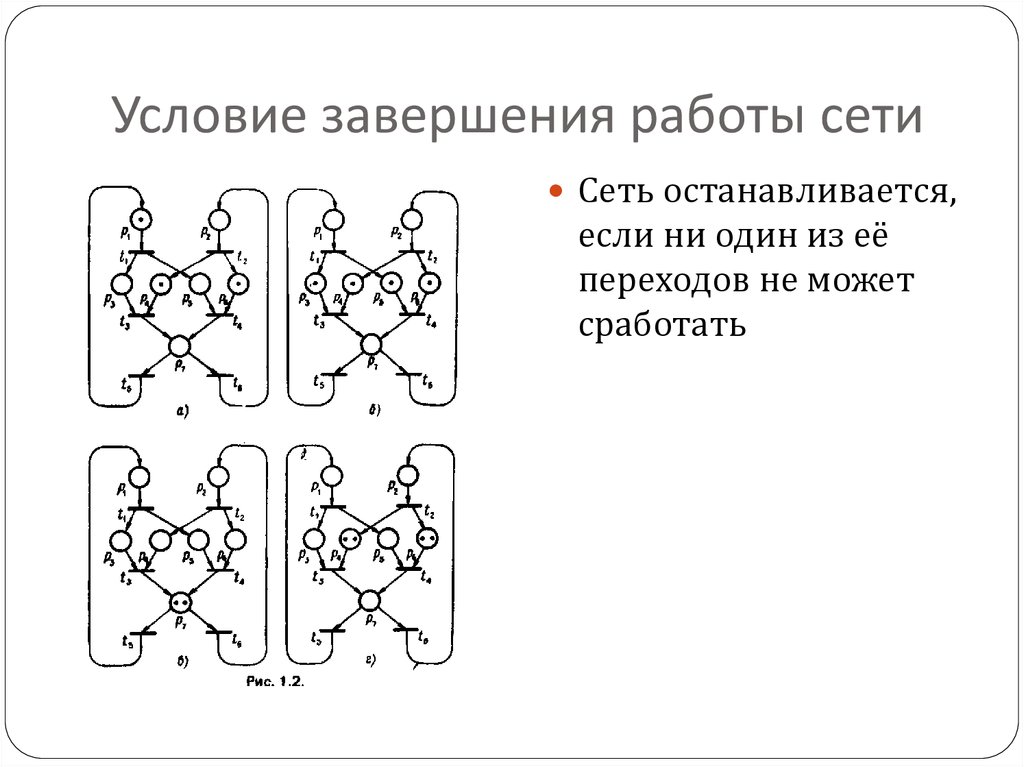
8. Условия

Причинно-следственные связи между
событиями в асинхронных моделях можно
реализовать указанием условий, при которых то
или иное событие может реализоваться
Примеры условий:
наличие данных для выполнения некоторой
операции в программе,
наличие деталей на конвейере,
появление сигнала на входе устройства
управления
Примером асинхронных моделей являются
сети Петри

9. Карл Адам Петри

Сетевая асинхронная
модель для
недетерминированных
систем была
предложена в 60-х
годах прошлого века
немецким математиком
Карлом Адамом Петри

10. Ёмкость условия

В модели Петри условия принято
характеризовать ёмкостью
Предполагается, что условие может быть:
не выполнено – ёмкость 0,
выполнено – ёмкость 1,
Выполнено с n-кратным запасом – ёмкость n
В терминах сетей Петри события называются
переходами, а условия – позициями
Предусловия реализации события – это входные
позиции для перехода, а постусловия – выходные
позиции

11. Теоретико-множественное определение сетей Петри

Введем понятие мультимножества, как
множества, допускающего вхождение
нескольких экземпляров одного и того же
элемента
Сеть Петри S является четверкой
S = (P, T, I, O), где
P – конечное множество позиций;
T – конечное множество переходов;
I – входная функция, сопоставляющая переходу
мультимножество его входных позиций;
O – входная функция, сопоставляющая переходу
мультимножество его входных позиций

12. Определения

Множество позиций:
P = {p1, p2, …, pn}, n ≥ 0;
Множество переходов:
T = {t1, t2, …, tm}, m ≥ 0;
Входная функция:
I: T → P*, где P*- мультимножество входных
позиций;
Выходная функция:
O: T → P*, где P*- мультимножество
выходных позиций;

13. Определения

Использование мультимножеств входных и
выходных позиций перехода, а не множеств,
позволяет позиции быть кратным входом и
кратным выходом перехода соответственно
При этом кратность определяется числом
экземпляров позиции в соответствующем
мультимножестве.
Структура сети Петри определяется ее
позициями, переходами, входной и выходной
функциями

14. Пример сети Петри

P = {p1, p2, p3},
T = {t1, t2},
I(t1) = {p1, p1, p2},
O(t1) = {p3},
I(t2) = {p1, p2, p2},
O(t2) = {p3}

15. Графы сетей Петри

Наглядным представлением сети Петри является её
графическое представление в виде двудольного,
ориентированного мультиграфа
Граф сети Петри обладает двумя типами узлов:
круг , представляющий позицию сети Петри,
планка, представляющая переход сети Петри
Ориентированные дуги этого графа соединяют
переход с его входными и выходными позициями
Дуги направлены от входных позиций к переходу и от
перехода к выходным позициям
В графе сети Петри невозможны дуги между двумя
позициями и между двумя переходами (двудольность)

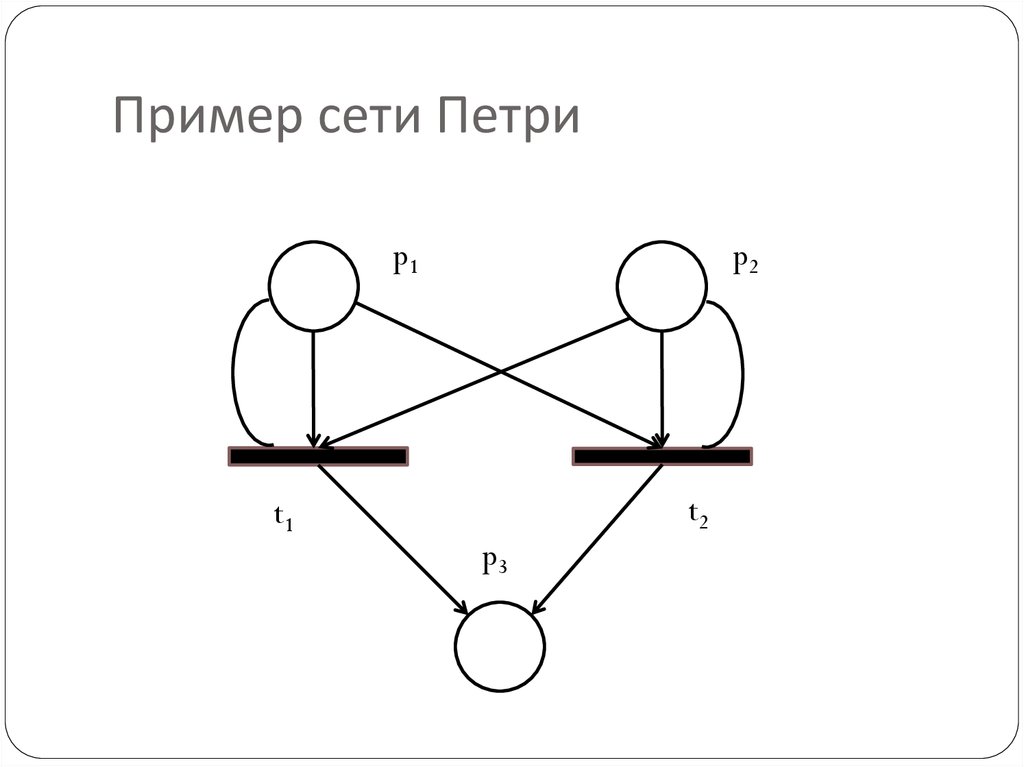
16. Пример сети Петри

p1
t1
p2
t2
p3

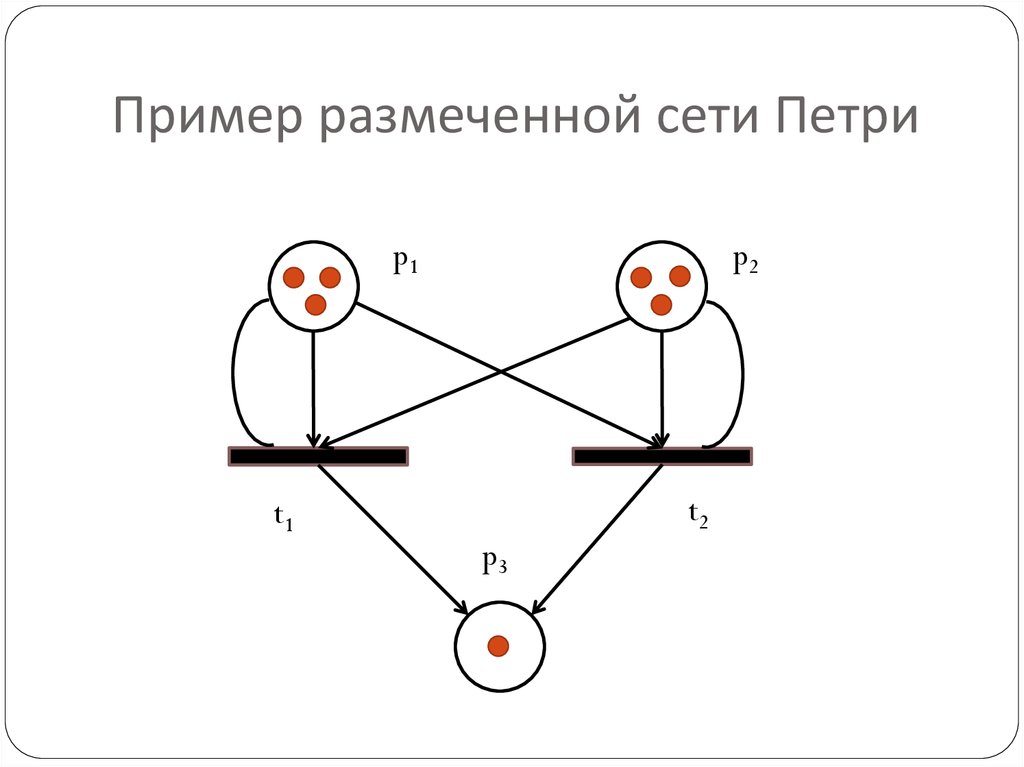
17. Разметка сетей Петри

В сетях Петри выполнение условий
изображается разметкой соответствующей
позиции путем размещения в ней числа фишек,
соответствующего ёмкости этой позиции
Фишки изображаются на графе точками;
количество фишек в позиции в процессе работы
сети Петри может изменяться от 0 до
бесконечности
Разметка μ сети Петри – это функция,
отображающая множество позиций P во
множество натуральных чисел N
μ: P → N

18. Разметка сетей Петри

Разметка , может быть также определена как n-
мерный вектор