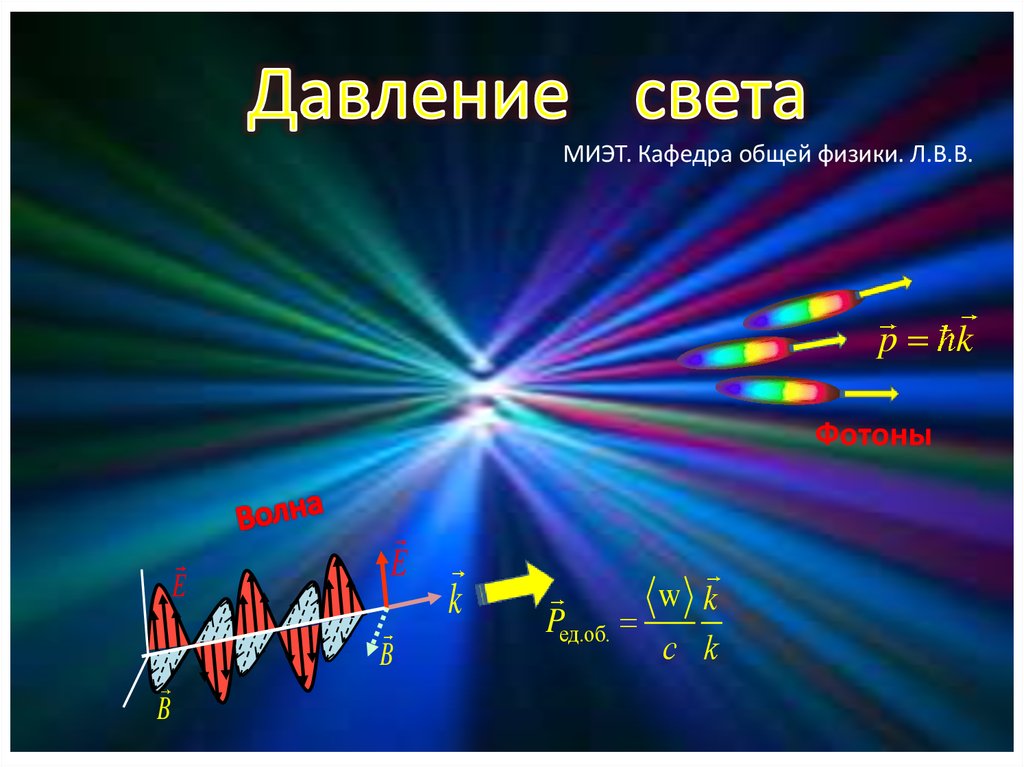
Давление света

1. Давление света

МИЭТ. Кафедра общей физики. Л.В.В.
p k
Фотоны
E
E
B
B
k
w k
Pед.об.
с k

2.

Историческая справка
И. Кеплер
1619г.
Немецкий ученый И. Кеплер
объяснил отклонение
хвостов комет, пролетающих
вблизи Солнца, световым
давлением.
1873г. Дж.Максвелл предсказал , что свет должен
оказывать давление при освещении поверхности тела.
E
Под действием электрического поля волны
электроны в телах совершают колебания –
образуется переменный электрический ток.
FE
Этот ток направлен вдоль напряженности E .
v
На упорядоченно движущиеся электроны действует
сила Лоренца
FЛ e v, B
FЛ
B
Дж. Максвелл
со стороны магнитного поля световой волны.
Сила FЛ , направленная в сторону распространения волны,
и есть сила светового давления.
2

3.

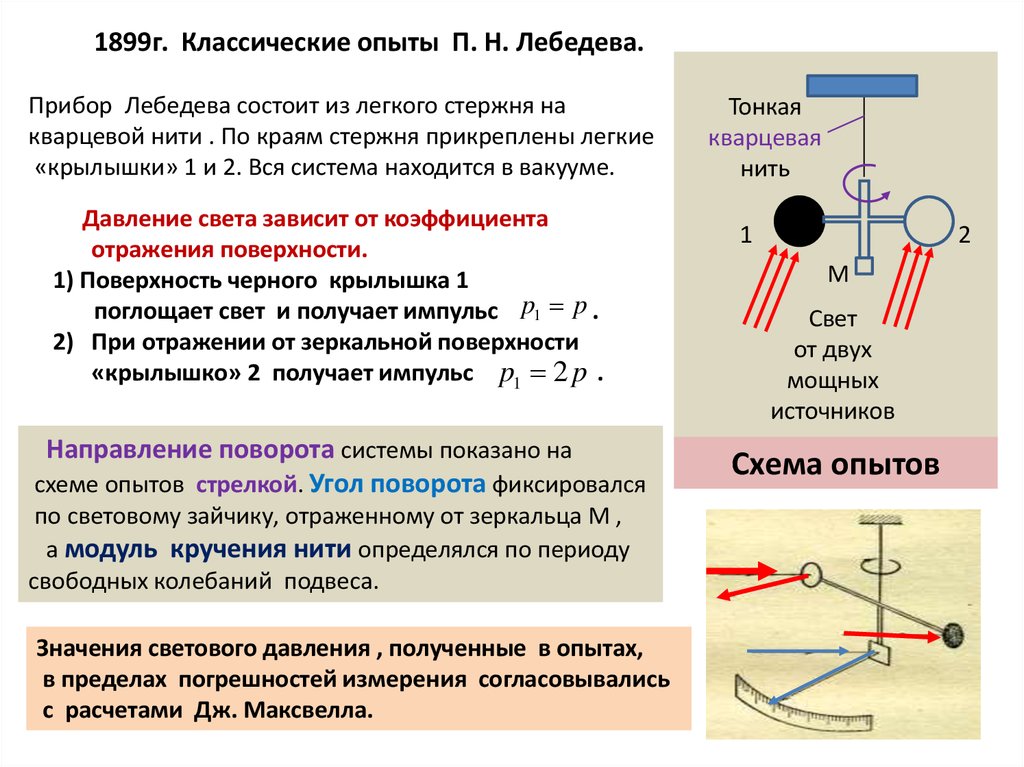
1899г. Классические опыты П. Н. Лебедева.
Прибор Лебедева состоит из легкого стержня на
кварцевой нити . По краям стержня прикреплены легкие
«крылышки» 1 и 2. Вся система находится в вакууме.
Давление света зависит от коэффициента
отражения поверхности.
1) Поверхность черного крылышка 1
поглощает свет и получает импульс p1 p .
2) При отражении от зеркальной поверхности
«крылышко» 2 получает импульс p1 2 p .
Направление поворота системы показано на
схеме опытов стрелкой. Угол поворота фиксировался
по световому зайчику, отраженному от зеркальца М ,
а модуль кручения нити определялся по периоду
свободных колебаний подвеса.
Значения светового давления , полученные в опытах,
в пределах погрешностей измерения согласовывались
с расчетами Дж. Максвелла.
Тонкая
кварцевая
нить
1
2
М
Свет
от двух
мощных
источников
Схема опытов

4.

Импульс электромагнитной волны.
Давление света с волновой точки зрения
С электромагнитной волной связан не только перенос энергии, но и
перенос импульса. Плотность потока энергии определяется вектором
jw EH , модуль которого равен jw w c .
Пойнтинга
Здесь E и HW – напряженности электрического и магнитного полей, w – плотность
электромагнитной энергии (энергия в единице объема) .Интенсивность волны I
определяется как среднее значение модуля плотности потока энергии:
I jw w c
Импульс единицы объема электромагнитной волны выражается через
2
вектор Пойнтинга как pед.об j c , модуль которого равен pед.об w c .
Импульс p , переданный при отражении и поглощении волны единице
поверхности в единицу времени, приводит к возникновению давления света
на поверхность: PD F S p S t , где F и p - проекции силы и
импульса на направление нормали к поверхности S .
Расчет давления при нормальном падении света на поверхность тела
приводит к формуле PD w (1 R) , где R – коэффициент отражения.
4

5.

Давление света с корпускулярной точки зрения
Давление света на освещаемое тело
объясняется передачей этому телу
импульса при отражении и
поглощении фотонов.
p k
Фотоны
Импульс фотона равен p k , модуль
которого p c , энергия фотона E pc .
Давление света
PD определяется как
Здесь S - площадь освещенной поверхности;
p
PD F S
F - перпендикулярная составляющая силы,
PD
действующей на поверхность;
S t
F p t
p - перпендикулярная составляющая
импульса, переданного телу в направлении нормали к поверхности.
5

6.

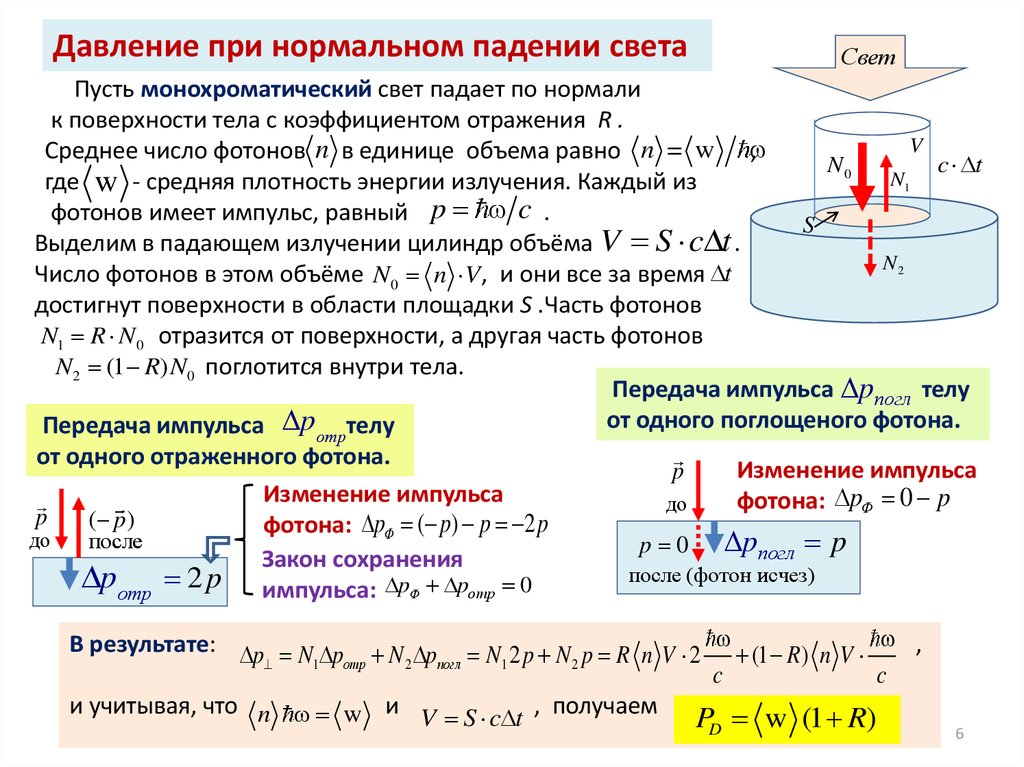
Давление при нормальном падении света
Свет
Пусть монохроматический свет падает по нормали
к поверхности тела с коэффициентом отражения R .
V
Среднее число фотонов n в единице объема равно n = w
,
c t
N0
N1
где w - средняя плотность энергии излучения. Каждый из
фотонов имеет импульс, равный p c .
S
Выделим в падающем излучении цилиндр объёма V S c t .
N2
Число фотонов в этом объёме N0 n V , и они все за время t
достигнут поверхности в области площадки S .Часть фотонов
N1 R N0 отразится от поверхности, а другая часть фотонов
N2 (1 R) N0 поглотится внутри тела.
Передача импульса pпогл телу
от одного поглощеного фотона.
Передача импульса pотртелу
от одного отраженного фотона.
Изменение импульса
p
Изменение импульса
фотона: pФ 0 p
до
p
( p)
фотона: pФ ( p) p 2 p
до
после
p 0 pпогл p
Закон сохранения
после (фотон исчез)
pотр 2 p импульса: pФ pотр 0
В результате: p N p N p N 2 p N p R n V 2 (1 R) n V ,
1
отр
2
погл
1
2
c
c
и учитывая, что n w и V S c t , получаем
PD w (1 R)
6

7.

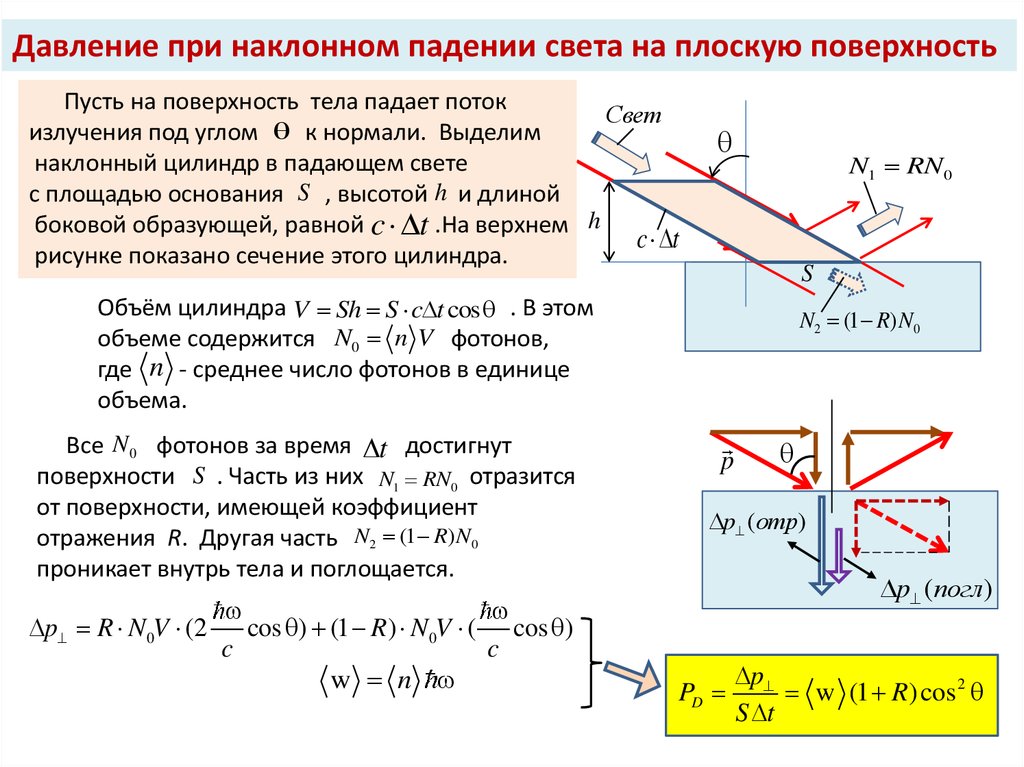
Давление при наклонном падении света на плоскую поверхность
Пусть на поверхность тела падает поток
Свет
излучения под углом к нормали. Выделим
наклонный цилиндр в падающем свете
с площадью основания S , высотой h и длиной
боковой образующей, равной c t .На верхнем h
c t
рисунке показано сечение этого цилиндра.
N1 RN 0
S
Объём цилиндра V Sh S c t cos . В этом
объеме содержится N0 n V фотонов,
где n - среднее число фотонов в единице
объема.
Все N 0 фотонов за время t достигнут
поверхности S . Часть из них N1 RN0 отразится
от поверхности, имеющей коэффициент
отражения R. Другая часть N2 (1 R) N0
проникает внутрь тела и поглощается.
p R N 0V (2
cos ) (1 R) N 0V ( cos )
c
c
w n
N2 (1 R) N0
p
p (отр)
p (погл)
PD
p
w (1 R) cos 2
S t

8.

Тангенциальная составляющая силы , действующей при поглощении света
Пусть свет падает на плоскую пластинку под
углом к его нормали. Коэффициенты отражения
и поглощения соответственно равны R и 1 R .
Исходя из корпускулярных представлений о свете как
потока фотонов, определим тангенциальную силу F ,
действующую со стороны падающего излучения
на единицу поверхности пластинки. Сила возникает
в результате поглощения фотонов, имеющих
тангенциальную составляющую импульса p (рисунок).
p
p
p
Введем единичный вектор , касательный к поверхности.
При отражении каждого фотона компоненты импульса,
перпендикулярные поверхности дают вклад в давление
света, а компоненты импульса p , параллельные поверхности,
дают вклад в суммарный переданный пластинке импульс p
и в тангенциальную составляющую силы F , действующей на
пластику параллельно вектору .
p

9.

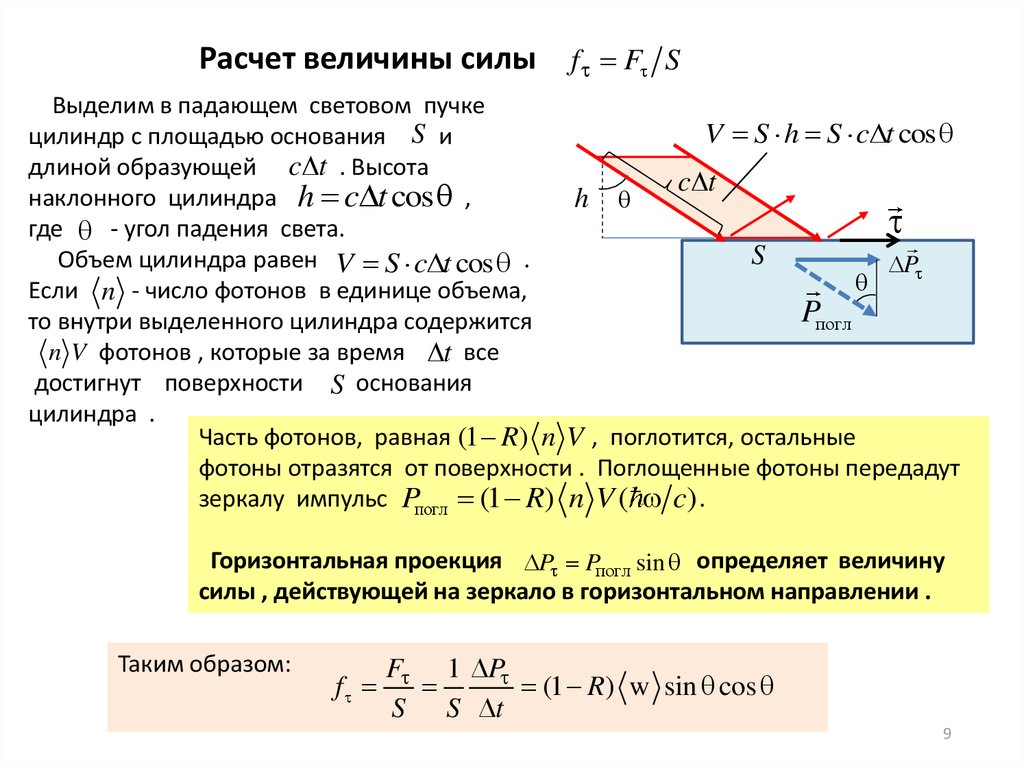
Расчет величины силы f F S
Выделим в падающем световом пучке
V S h S c t cos
цилиндр с площадью основания S и
длиной образующей c t . Высота
c t
наклонного цилиндра h c t cos ,
h
где - угол падения света.
S
Объем цилиндра равен V S c t cos .
P
Если n - число фотонов в единице объема,
Pпогл
то внутри выделенного цилиндра содержится
n V фотонов , которые за время t все
достигнут поверхности S основания
цилиндра .
Часть фотонов, равная (1 R) n V , поглотится, остальные
фотоны отразятся от поверхности . Поглощенные фотоны передадут
зеркалу импульс Pпогл (1 R) n V ( c) .
Горизонтальная проекция P Pпогл sin определяет величину
силы , действующей на зеркало в горизонтальном направлении .
Таким образом:
F 1 P
f
(1 R) w sin cos
S S t
9

10.

Измерение тангенциальной силы
в эксперименте
Схема прибора, с помощью
которого можно измерить
горизонтальную составляющую
силы, действующей со стороны
направленного пучка света,
показана на рисунке.
F
Свет
Свет
Точка
F
подвеса
Световой пучок падает на легкие пластиночки, укрепленные
перпендикулярно на несущем стержне.
Угол падения выбирается равным 450 , так как F cos sin .
Тангенциальные составляющие силы создают вращающий момент
относительно точки подвеса, тогда как нормальные силы давления не
сообщают подвесу вращающего момента.
10

11.

Давление лазерного излучения
Интерес к световому давлению снова появился после изобретения лазеров.
На рисунке показана схема эксперимента с
лазером мощностью 250 МВт. Прозрачная
стеклянная сфера диаметром 20 мкм висит в
воздухе над стеклянной пластиной на высоте
около 1 см над её поверхностью. Хотя частица
очень мала и еле различима невооруженным глазом,
в опыте она легко обнаруживается по яркому сиянию
из-за рассеяния на ней света лазера.
Лазерное излучение можно сфокусировать в область
с площадью поперечного сечения с радиусом порядка
длины волны генерации . Давление в фокусе мощного
лазерного излучения может достигать сотен атмосфер.
Лазер
Схема эксперимента
Лазер на рубине излучает в импульсе длительностью 0,5мс
энергию 1 Дж на длине волны 694 нм в виде почти параллельного
Пример.
пучка света с сечением S 1см2 . Давление сфокусированного пучка
света при нормальном падении на черную поверхность тела составляет
примерно 150 атм.
11

12.

Световое давление лазерного излучения достигает значительной величины , и
частицы диаметром от 0,1 до 100 мкм в лазерном луче могут получать ускорение, в
десятки тысяч раз превышающее ускорение свободного падения.
Давление лазерного излучения может использоваться для решения многих
актуальных задач атомной физики, например для ускорения в высоком вакууме
малых частиц до очень больших скоростей, разделения газов разной массы.
Датчики давления
Механотроны
Помимо крутильных весов по методу Лебедева для измерения светового
давления используются механотроны, которые представляют собой
электровакуумный прибор с механически управляемыми электродами.
При воздействии внешнего механического сигнала в механотроне
происходит перемещение одного или нескольких подвижных электродов,
что вызывает соответствующее изменение анодного тока.
Механотроны обычно применяют для измерения больших уровней мощности
и энергии импульсов лазерного излучения, например непрерывного
излучения мощных СО 2 -лазеров и импульсного на стекле с неодимом
Современные устройства позволяют измерять мощность лазерного излучения,
начиная с мощности от единиц милливатт .
12

13.

Микроэлектронный датчик давления лазерного излучения
Для измерения светового лазерного давления используются пьезорезистивный датчики
давления, изготавливаемые по технологии микро-электро-механических систем (МЭМС)
на кремниевой подложке.
Датчик
Датчики
Датчик имеет тонкую кремниевую
давления
мембрану, герметично закрывающую
расположенную под ней полость, и четыре
сформированных на ее поверхности
пьезорезистора , сопротивление которых
зависит от давления и температуры.
Мембрана
Деформация
Лазерное
излучение
Внешнее
давление
Мембрана
Вид сбоку
Выход
Вход
Любое отклонение внешнего давления от давления
внутри полости вызывает деформацию мембраны и
изменение сопротивления пьезорезисторов, которые
соединяются по мостовой схеме. Усилители,
сформированные на общей с датчиком кремниевой
подложке, формируют выходной сигнал.
13

14.

Примеры решения задач
Задача 1. Лазер излучил в импульсе длительностью 0,13 мс пучок света
с энергией Е = 10 Дж. Какое среднее давление будет оказывать такой световой
импульс, если его сфокусировать в пятно с радиусом r = 5 мкм на поверхность,
перпендикулярную к пучку, с коэффициентом отражения R = 0,50.
Решение. Форма светового пучка вблизи фокуса показана на рисунке.
Давление света PD при нормальном падении
на поверхность с площадкой S вычисляется
по формуле
I
PD w (1 R) (1 R ) ,
c
где
I w c, Вт м 2
В результате получаем :
E
.
S
PD
S r 2
E
(1 R)
2
r c
50 105 Па (50 атм) .
14

15.

Задача 2. В опыте Лебедева крестовина подвешена на тонкой
Нить
кварцевой нити. Момент силы кручения M F k , где
11
постоянная кручения нити k 2, 2 10 Н м рад. , - угол
M
поворота крестовины, измеряемый по отклонению светового
зайчика, отраженного от зеркальца М. На крестовине закреплены
два кружка из платиновой фольги, один из них зачернен, другой
оставлен блестящим с коэффициентом отражения света R=0,5.
Диаметр кружков d=5 мм, Расстояние от центра кружков до оси
вращения l 9, 2 мм . Какое давление оказывает свет от дуговой лампы, если
при освещении блестящего кружка отклонение зайчика от зеркальца М равно
x=76 мм по шкале, удаленной на расстояние L=1200 мм.
Решение. Световое давление PD F S . Из условия равенства моментов при
отклонении на угол
найдем силу светового давления:
F l k
F k l
Из рисунка следует, что при малых углах поворота:
tg , x 2L x
L
M
Учитывая, что S d 2 4 , окончательно получаем
2k x
PD
(1 R) 5,8 мкПа
l L d 2
15