Similar presentations:
Частотно-временная область ЦИТ
1. ЦИФРОВАЯ ИЗМЕРИТЕЛЬНАЯ ТЕХНИКА ГЛАВА 2: ЧАСТОТНО-ВРЕМЕННАЯ ОБЛАСТЬ ЦИТ
В.Г. Кнорринг1
2. ГЛАВА 2. ЧАСТОТНО-ВРЕМЕННАЯ ОБЛАСТЬ ЦИТ
Содержание:• Объекты и шкалы частотно-временнóй
области
• Преобразования длительность→код и
код→длительность (включая цифровую
широтно-импульсную модуляцию)
• Преобразования частота→код и код→частота
Специфическая область цифровых фазовых
измерений в курс не включена.
2
3. ОБЪЕКТЫ ЧАСТОТНО-ВРЕМЕННǑЙ ОБЛАСТИ
Исходные понятия: процесс и событие.Событие может быть отрезком или состоянием
процесса, но может и не зависеть от процесса.
Процессы и события представляются сигналами.
В сигнале выделяется информативный
параметр − обычно электрическое напряжение.
Изменение информативного параметра
описывается сигнальной функцией, обычно её
называют просто сигналом.
3
4. АБСТРАКЦИИ И ПАРАМЕТРЫ, СВЯЗАННЫЕ С СОБЫТИЯМИ (НЕ ПО ГОСТ 8.567−2014 !)
Абстрактное бесконечно короткое событие −момент времени.
Расстояние во времени между двумя
моментами − интервал времени.
Параметр, характеризующий положение
момента во времени − дата.
Операция нахождения даты − датирование
события.
Параметр, характеризующий интервал
времени − длительность интервала.
Операция нахождения длительности интервала −
измерение длительности.
4
5.
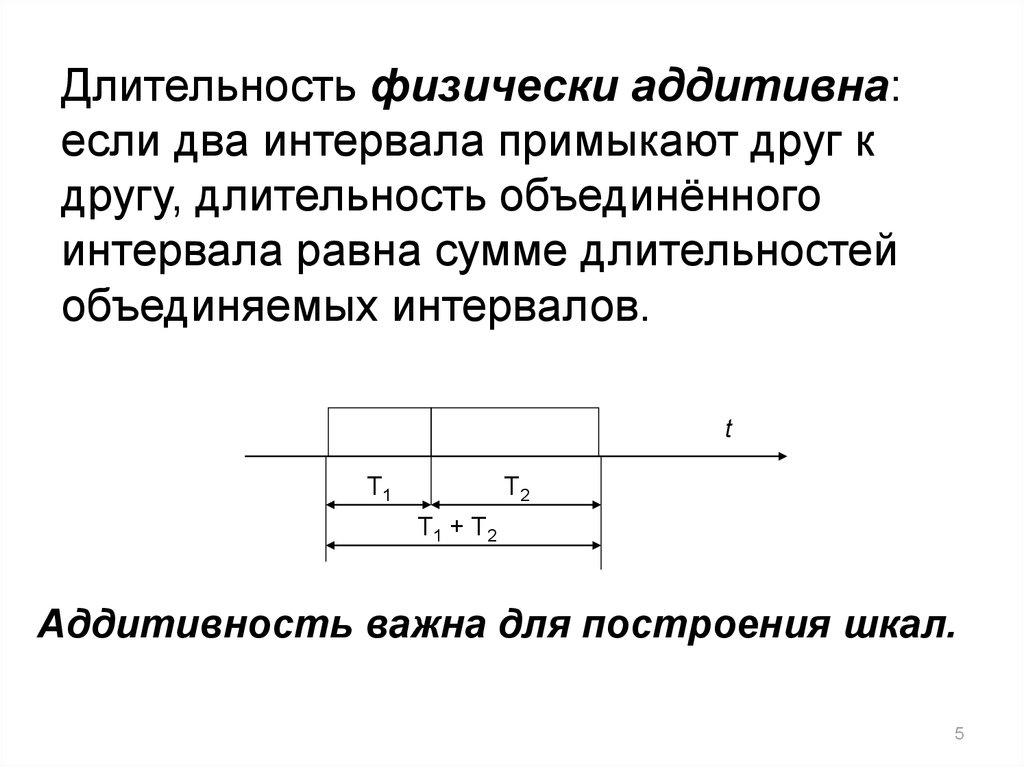
Длительность физически аддитивна:если два интервала примыкают друг к
другу, длительность объединённого
интервала равна сумме длительностей
объединяемых интервалов.
t
T1
T2
T1 + T2
Аддитивность важна для построения шкал.
5
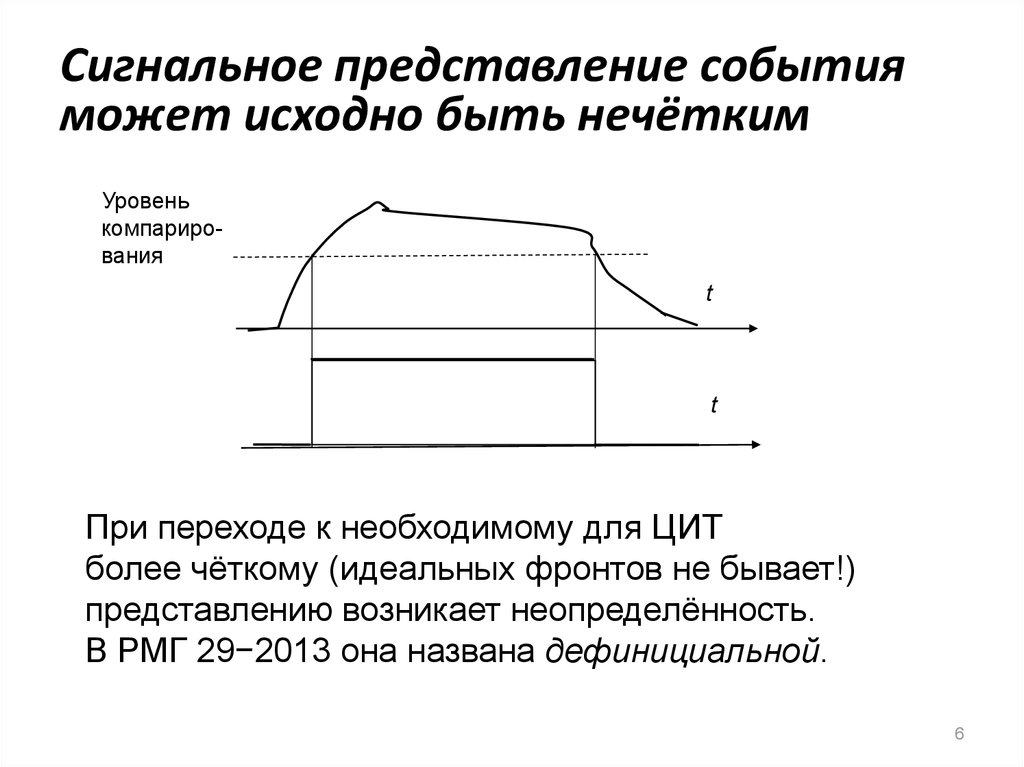
6. Сигнальное представление события может исходно быть нечётким
Уровенькомпарирования
t
t
При переходе к необходимому для ЦИТ
более чёткому (идеальных фронтов не бывает!)
представлению возникает неопределённость.
В РМГ 29−2013 она названа дефинициальной.
6
7. НЕКОТОРЫЕ ВИДЫ ПРОЦЕССОВ
Наиболее общим считается случайныйпроцесс.
Для ЦИТ важны циклические процессы,
многократно проходящие однотипные
последовательности состояний.
Идеальный частный случай циклического
процесса − периодический процесс:
t : x(t ) x(t T ).
Минимальное ненулевое T в этой формуле
есть период процесса.
7
8.
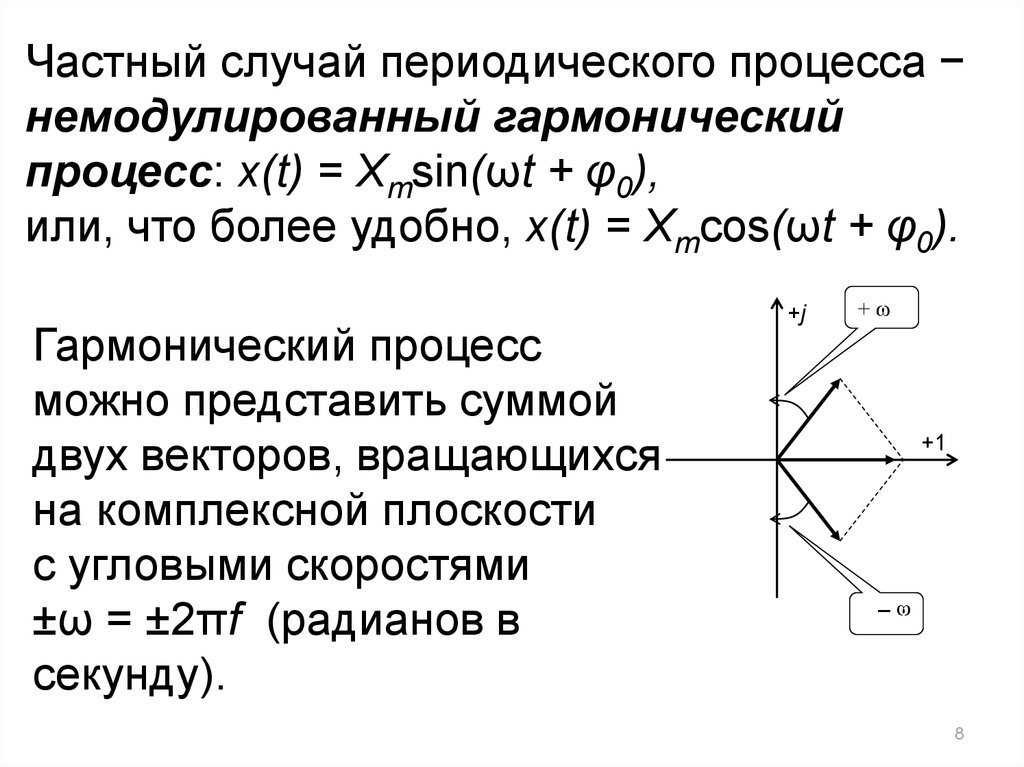
Частный случай периодического процесса −немодулированный гармонический
процесс: x(t) = Xmsin(ωt + φ0),
или, что более удобно, x(t) = Xmcos(ωt + φ0).
+ω
+1
ω–
Гармонический процесс
можно представить суммой
двух векторов, вращающихся
на комплексной плоскости
с угловыми скоростями
±ω = ±2πf (радианов в
секунду).
+j
8
9.
Полный угловой путь, пройденныйвращающимся вектором − это фаза Φ.
При отсутствии модуляции Φ = ωt + φ0.
При модуляции амплитуда или скорость
вращения векторов зависит от времени.
Для ЦИТ важна угловая (частотная или
t
фазовая) модуляция.
При частотной модуляции ( )d
Тогда сигнальная функция
принимает вид:
t
0
x(t ) X m cos[ 2πf ( )d 0 ].
0
0 .
9
10.
Модулированный процесс в общем случаене является периодическим (но остаётся
циклическим). Практики условно называют цикл
процесса “периодом”, понимая, что его
длительность изменяется во времени.
Особый вид объектов частотно-временнóй
области − потоки событий. Они могут быть
детерминированными и случайными.
Важнейшим параметром процессов является
частота. Для разных видов процессов
(и потоков событий) её определения
различаются.
10
11. ОПРЕДЕЛЕНИЯ ЧАСТОТЫ (термины не общеприняты!)
Периодический процесс (любой формы)характеризуется хронометрической
частотой
1
f .
T
Частотно модулированный процесс
в общем случае непериодичен. Для него
вводится фазовая частота
1 d
f
.
2 dt
11
12.
Для произвольного непериодическогопроцесса спектральная частота может
быть определена как переменная
в преобразовании Фурье.
Потоки событий характеризуются
статистической частотой
f lim Tи
N (Tи )
.
Tи
Здесь Tи − измерительный интервал
(интервал усреднения); N − число
событий в этом интервале.
12
13.
Разные определения частоты могут даватьразные результаты.
У сигнала в форме меандра одна
хронометрическая и совпадающая с ней
статистическая частота, но множество
спектральных частот. Его фазу приходится
считать квантованной, изменяющейся скачками,
и тогда частота представляется
последовательностью δ-импульсов.
У сигнала в виде повторяющихся пар
импульсов статистическая частота вдвое
выше хронометрической.
13
14.
Только фазовая частота можетнепрерывно меняться во времени.
Только статистическая частота аддитивна
(и то лишь при условии, что события
объединяемых потоков не совпадают).
Сложение или вычитание фазовых частот
выполняют с использованием формулы:
1
1
cos 1t cos 2t cos( 1 2 )t cos( 1 2 )t.
2
2
Нужную составляющую выделяют фильтром.
14
15. ШКАЛЫ ВРЕМЕНИ
Шкалы времени используются длядатирования событий и для измерения
длительности интервалов времени.
Метрологи занимаются шкалами всемирного
времени.
Для ЦИТ представляют интерес шкалы времени
“местного значения”, реализуемые в приборах
и модулях.
15
16. ОСОБЕННОСТИ ШКАЛ ВРЕМЕНИ В ЦИТ
Стабилизаторы тока, образующие шкалу вбыстродействующем ЦАП, или резисторы,
образующие шкалу в цифровом мосте,
требуют индивидуальной подгонки.
Во временнóй области природа нас
“бесплатно” снабдила шкалами циклов
процессов, близких к периодическим.
Они высокостабильны (нестабильность
хорошего кварцевого генератора 10−7) и
равномерны. Индивидуальная подгонка циклов,
конечно, не требуется.
16
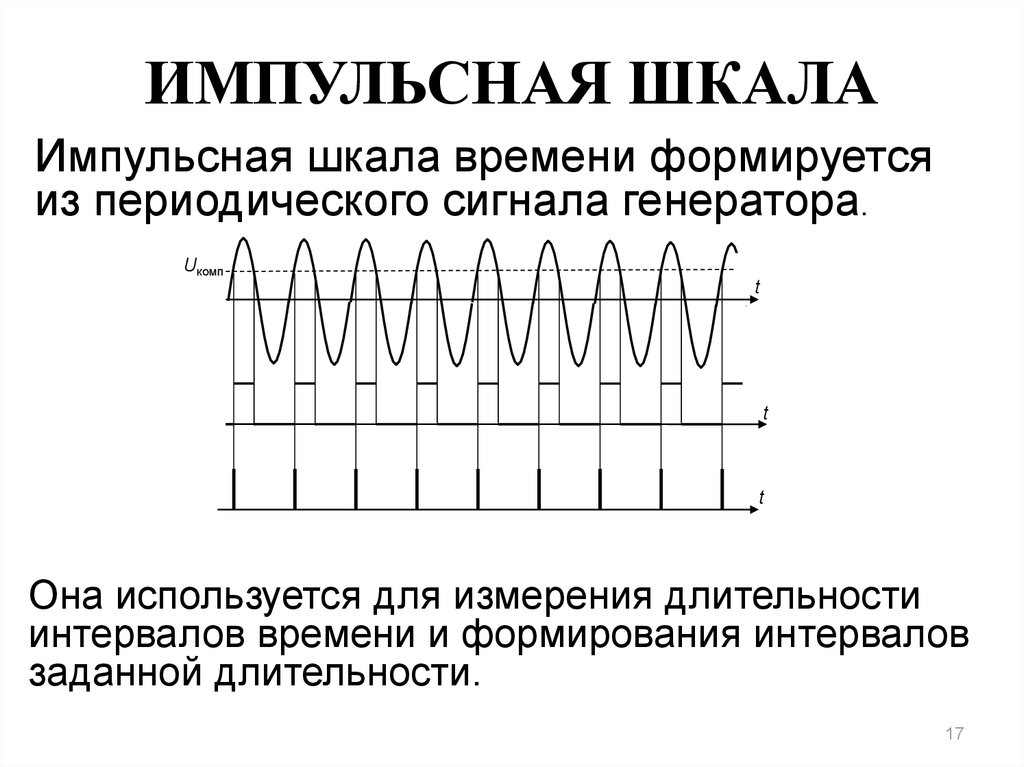
17. ИМПУЛЬСНАЯ ШКАЛА
Импульсная шкала времени формируетсяиз периодического сигнала генератора.
Uкомп
t
t
t
Она используется для измерения длительности
интервалов времени и формирования интервалов
заданной длительности.
17
18. ШКАЛЫ СТРОБОВ
Шкалы стробов формируются изимпульсных шкал с помощью счётчиков
разного рода. Они используются для
датирования событий.
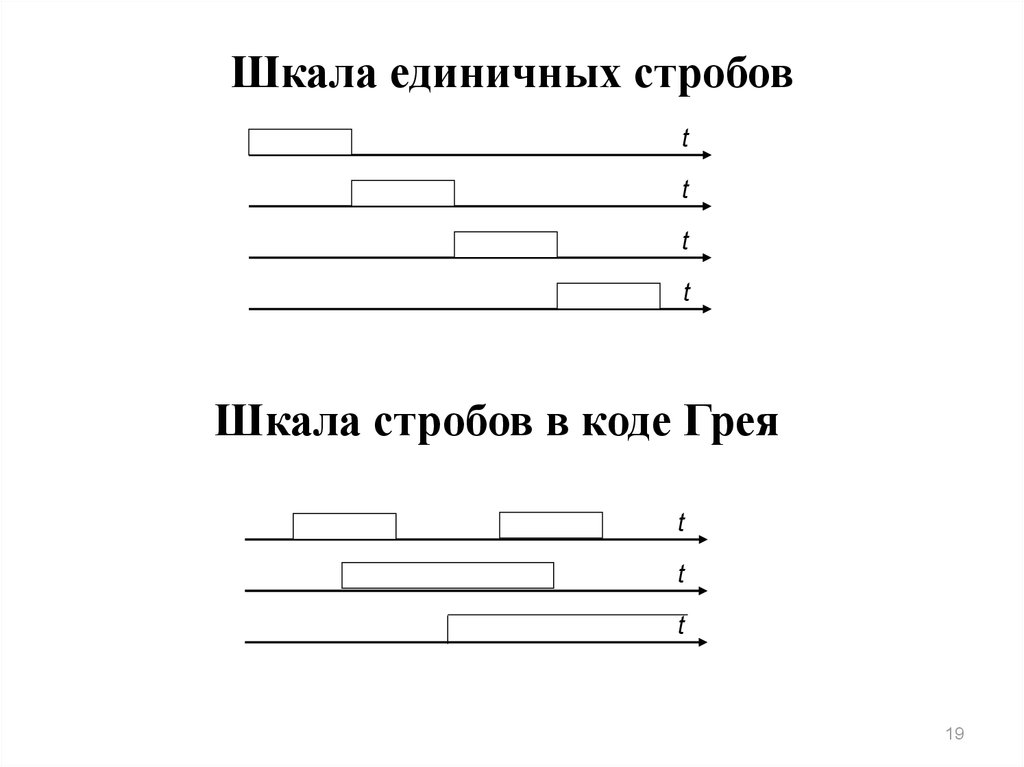
Возможны последовательности
единичных стробов, но чаще встречаются
комбинации стробов, образующие
натуральный двоичный код, код Грея
и т. п.
18
19.
Шкала единичных стробовt
t
t
t
Шкала стробов в коде Грея
t
t
t
19
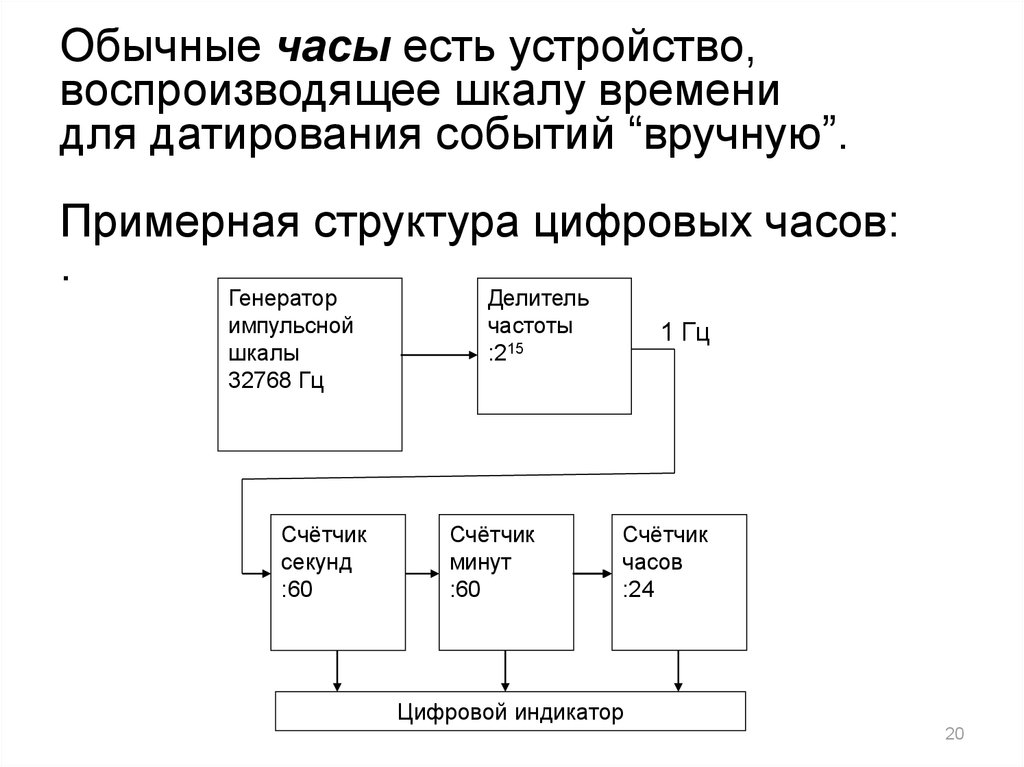
20.
Обычные часы есть устройство,воспроизводящее шкалу времени
для датирования событий “вручную”.
Примерная структура цифровых часов:
.
Генератор
импульсной
шкалы
32768 Гц
Счётчик
секунд
:60
Делитель
частоты
:215
Счётчик
минут
:60
1 Гц
Счётчик
часов
:24
Цифровой индикатор
20
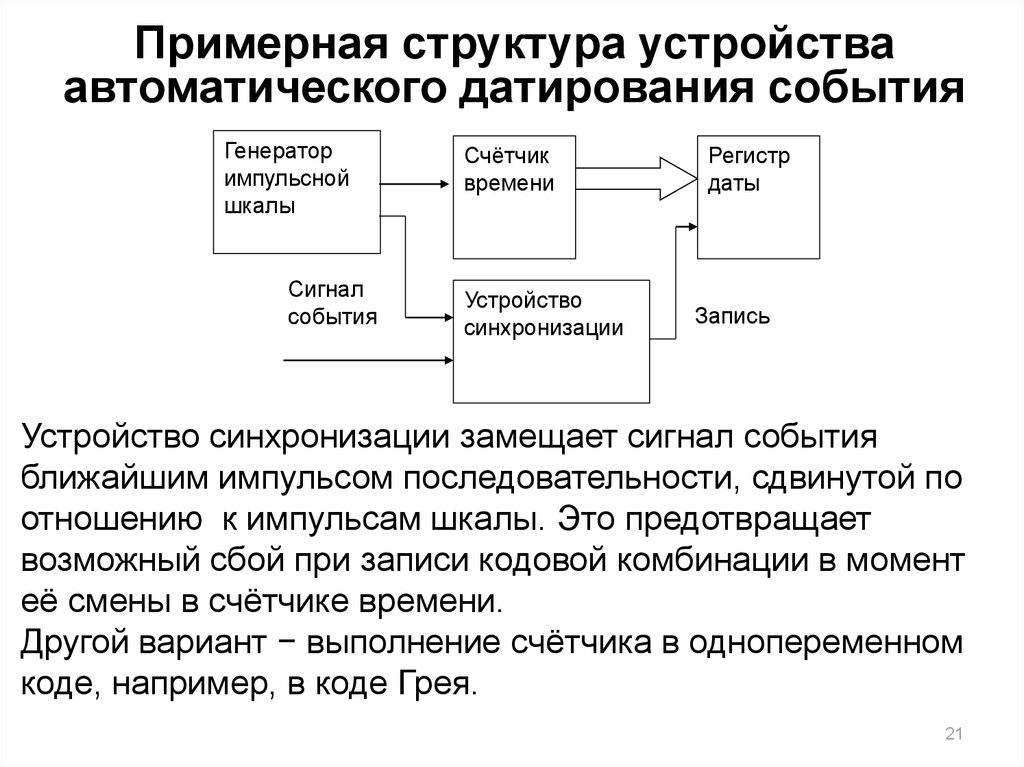
21. Примерная структура устройства автоматического датирования события
Генераторимпульсной
шкалы
Сигнал
события
Счётчик
времени
Устройство
синхронизации
Регистр
даты
Запись
Устройство синхронизации замещает сигнал события
ближайшим импульсом последовательности, сдвинутой по
отношению к импульсам шкалы. Это предотвращает
возможный сбой при записи кодовой комбинации в момент
её смены в счётчике времени.
Другой вариант − выполнение счётчика в однопеременном
коде, например, в коде Грея.
21
22. Таким образом, есть две возможности избежать сбоев при чтении изменяющихся кодовых комбинаций.
Сбои могут возникнуть в моменты сменынескольких знаков в кодовой комбинации,
например, 10011111→10100000. Такие
переходы назовём опасными границами.
Два способа избежать сбоев таковы:
1. Отодвинуть операцию считывания от
опасной границы (во временнóй области это
достигается синхронизацией).
2. Использовать однопеременный код, не
имеющий опасных границ.
Те же два способа встретятся нам
в пространственной области.
22
23.
Возможная схема устройствасинхронизации приведена в книге:
Гутников В.С. Интегральная электроника
в измерительных устройствах. − Л.:
Энергоатомиздат. Лен. отделение, 1988
(в последующих ссылках − Гутников, 1988).
См. рис. 6.8 на странице 177 этой книги.
Обратим внимание на то, что в схеме
Гутникова задержка возврата второго
триггера в исходное состояние может
вызвать появление короткого ложного
импульса!
23
24. ПРЕОБРАЗОВАНИЕ ДЛИТЕЛЬНОСТЬ→КОД
Числовое значение длительности находитсяпутём заполнения сформированного строба
импульсами шкалы. В этой ситуации их называют
квантующими импульсами или метками
времени. Полагаем, что каждая метка “отвечает”
за предыдущий цикл шкалы.
Сравнивающим устройством является элемент И.
Tx
t
t
T0
24
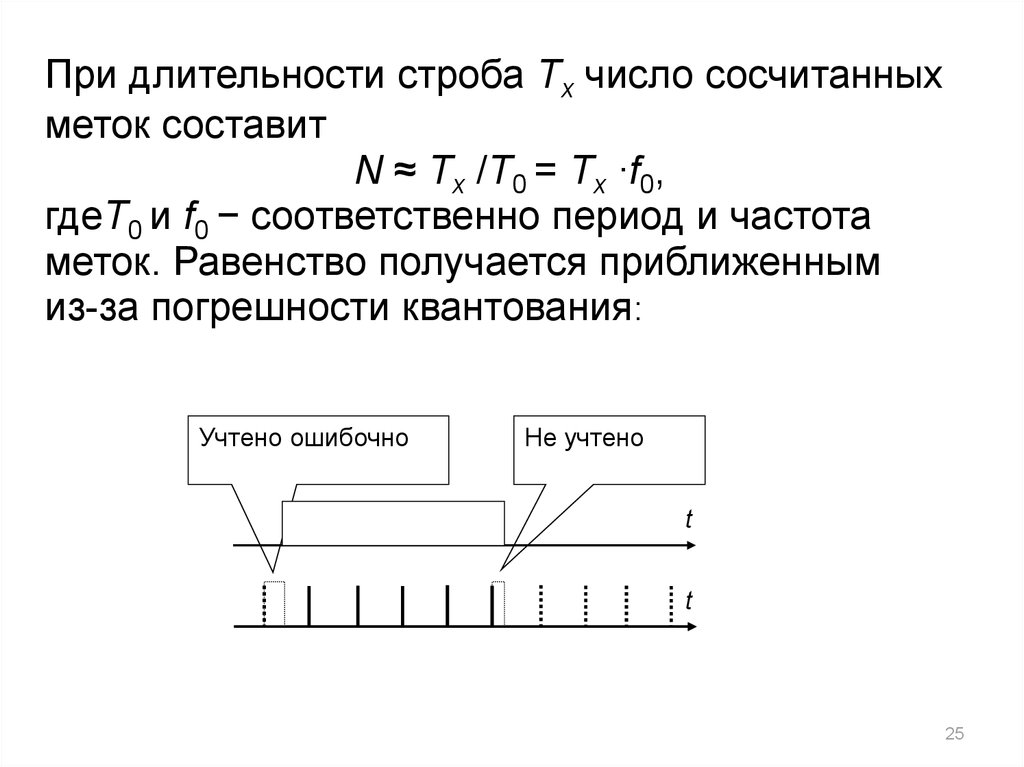
25.
При длительности строба Tx число сосчитанныхметок составит
N ≈ Tx /T0 = Tx ∙f0,
гдеT0 и f0 − соответственно период и частота
меток. Равенство получается приближенным
из-за погрешности квантования:
Учтено ошибочно
Не учтено
t
t
25
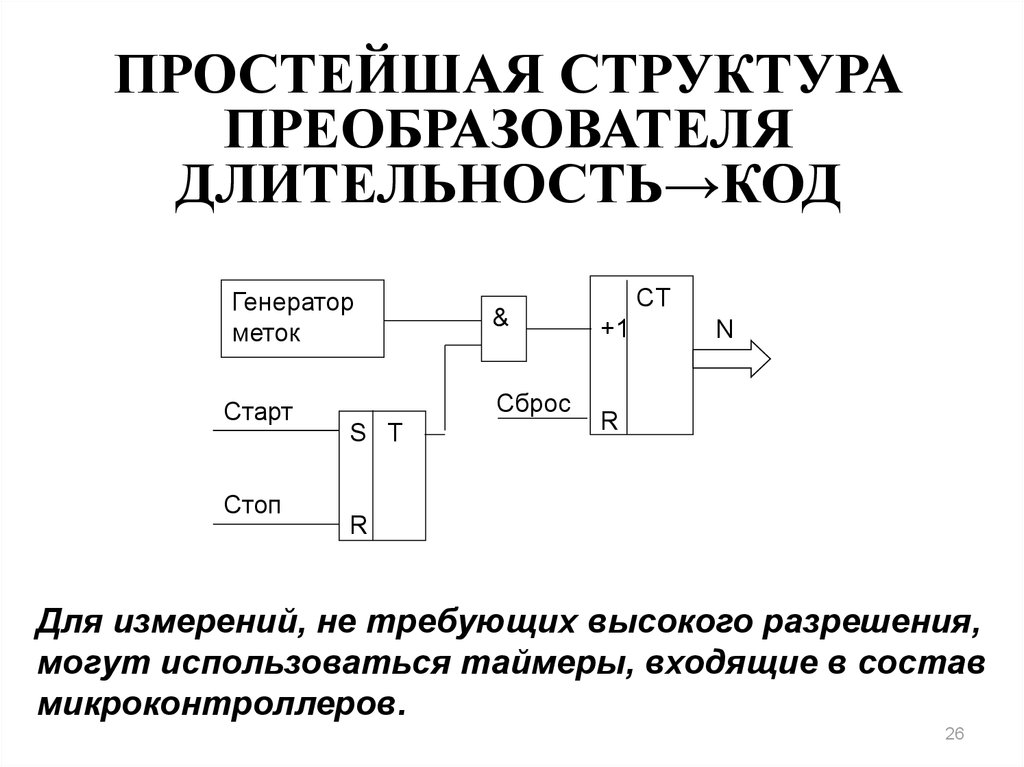
26. ПРОСТЕЙШАЯ СТРУКТУРА ПРЕОБРАЗОВАТЕЛЯ ДЛИТЕЛЬНОСТЬ→КОД
Генераторметок
Старт
Стоп
&
Сброс
S T
CT
+1
N
R
R
Для измерений, не требующих высокого разрешения,
могут использоваться таймеры, входящие в состав
микроконтроллеров.
26
27. СОСТАВ ПОГРЕШНОСТЕЙ ПРЕОБРАЗОВАТЕЛЯ
Погрешности, общие для всехпреобразователей аналог→код:
• Погрешность меры, всегда входящая
в результат как мультипликативная
(в данном случае − нестабильность
частоты меток);
• Погрешность квантования, обычно
аддитивная.
В данном случае может добавиться
дефинициальная неопределённость.
Разность задержек в триггере и влияние
конечной длительности считаемых импульсов
в современных цифровых приборах
практически не сказываются.
27
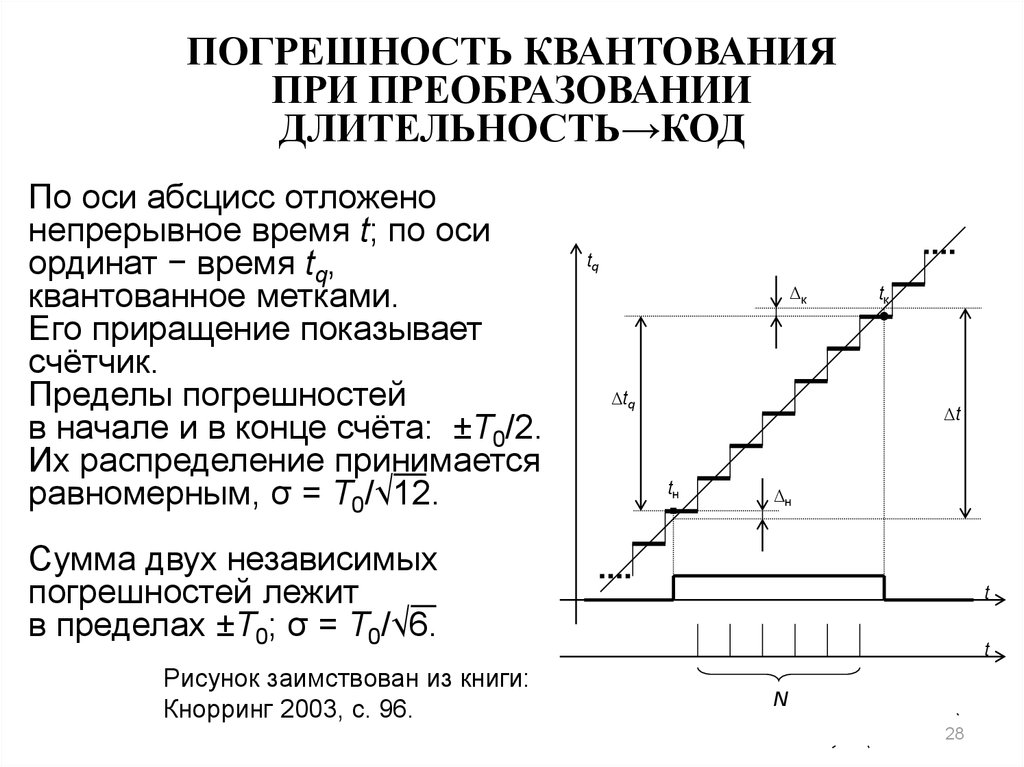
28. ПОГРЕШНОСТЬ КВАНТОВАНИЯ ПРИ ПРЕОБРАЗОВАНИИ ДЛИТЕЛЬНОСТЬ→КОД
По оси абсцисс отложенонепрерывное время t; по оси
ординат − время tq,
квантованное метками.
Его приращение показывает
счётчик.
Пределы погрешностей
в начале и в конце счёта: ±T0/2.
Их распределение принимается
равномерным, σ = T0/√12.
tq
Δк
Δtq
tк
Δt
tн
Δн
Сумма двух независимых
погрешностей лежит
в пределах ±T0; σ = T0/√6.
Рисунок заимствован из книги:
Кнорринг 2003, с. 96.
t
t
N
28
29. ПРИМЕНЕНИЯ ПРЕОБРАЗОВАТЕЛЕЙ ДЛИТЕЛЬНОСТЬ→КОД
• Режим преобразования длительность→код предусматривается во всех
счётчиковых частотомерах общего
назначения.
• Первые электронные цифровые
вольтметры были в основном
«время−импульсными».
• Измерения малых длительностей
нужны в ультразвуковых, оптических
и радиодальномерах; они требуются
также в физических экспериментах.
29
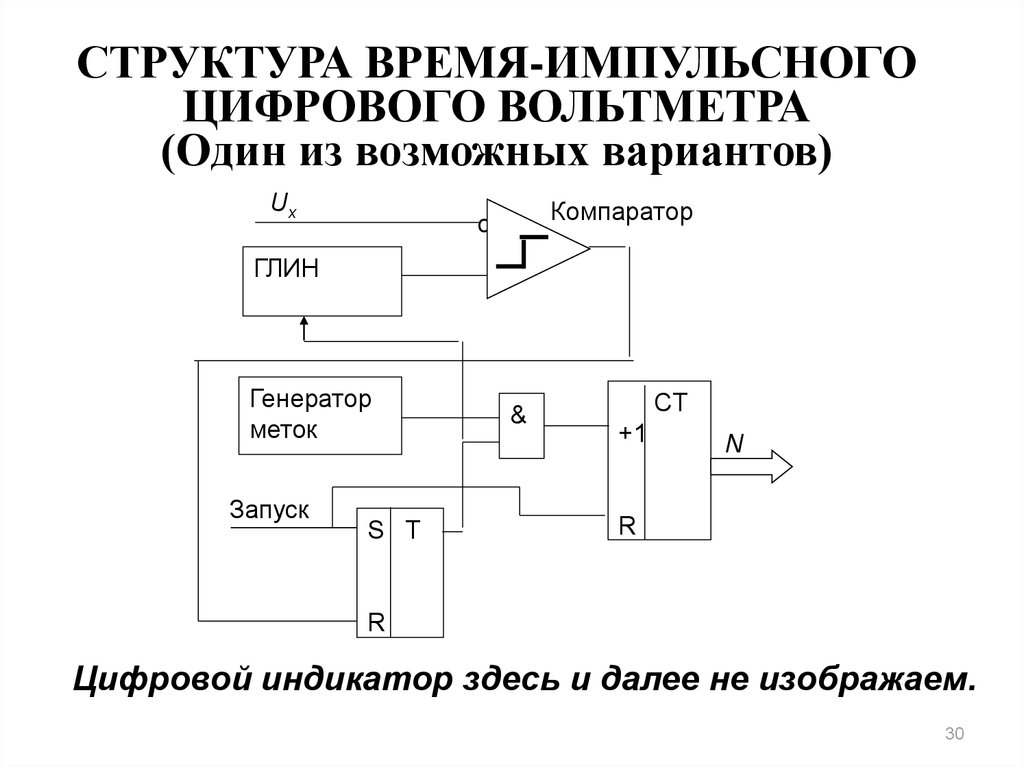
30. СТРУКТУРА ВРЕМЯ-ИМПУЛЬСНОГО ЦИФРОВОГО ВОЛЬТМЕТРА (Один из возможных вариантов)
UxКомпаратор
о
ГЛИН
Генератор
меток
Запуск
S T
&
CT
+1
N
R
R
Цифровой индикатор здесь и далее не изображаем.
30
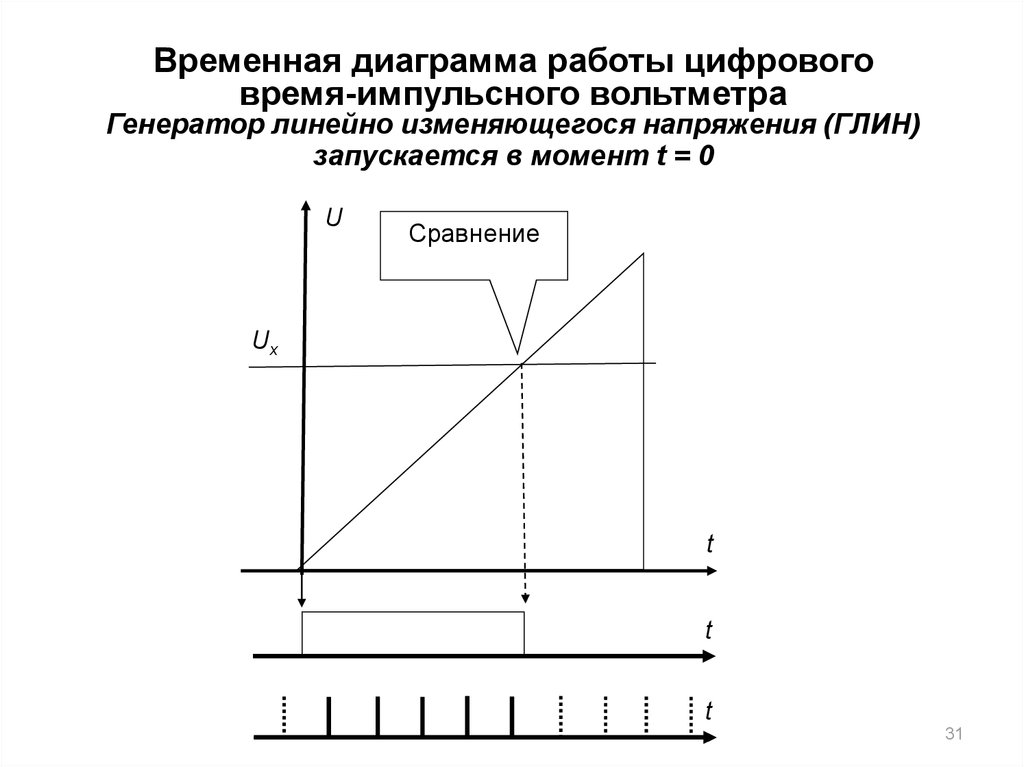
31. Временная диаграмма работы цифрового время-импульсного вольтметра Генератор линейно изменяющегося напряжения (ГЛИН) запускается
в момент t = 0U
Сравнение
Ux
t
t
t
31
32. Выведите самостоятельно формулу, связывающую число N сосчитанных импульсов с измеряемым напряжением Ux
Для этого примите, что ток, заряжающийконденсатор (ёмкостью C) генератора линейно
изменяющегося напряжения ГЛИН, задаётся
источником опорного напряжения UREF и
резистором R, а частота меток времени равна fo.
Учтите в формуле погрешность квантования
±1 импульс. Какие ещё составляющие
погрешности выявляются формулой?
Нет ли составляющих, которые ею не
выявляются?
32
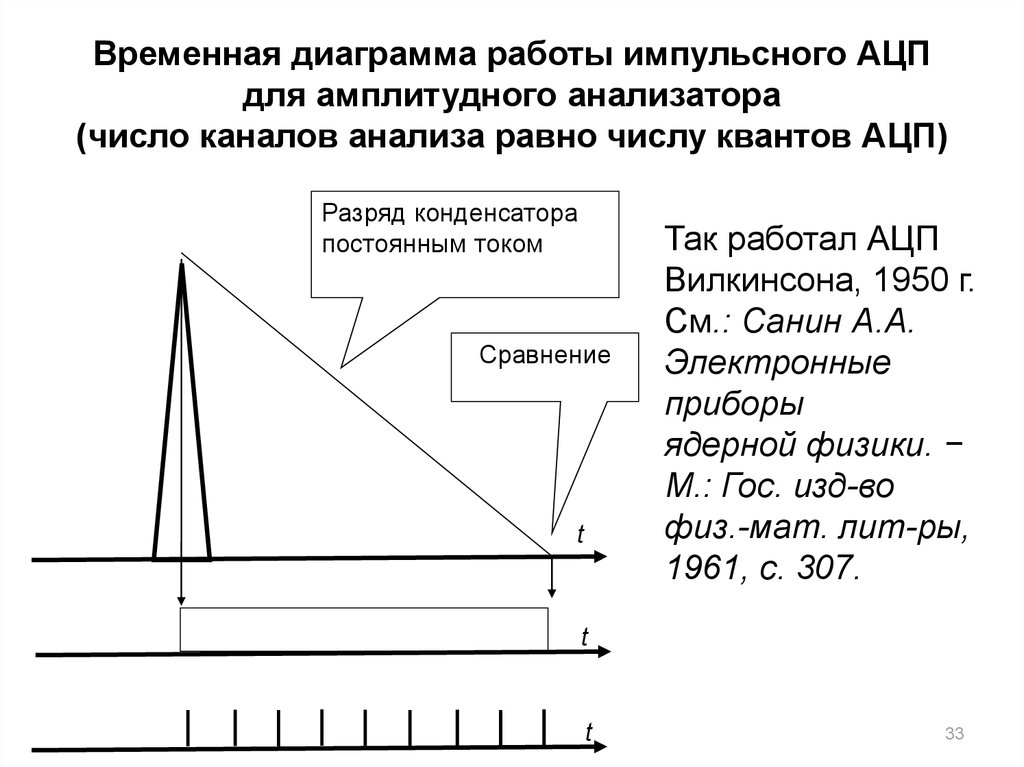
33. Временная диаграмма работы импульсного АЦП для амплитудного анализатора (число каналов анализа равно числу квантов АЦП)
Разряд конденсаторапостоянным током
Сравнение
t
Так работал АЦП
Вилкинсона, 1950 г.
См.: Санин А.А.
Электронные
приборы
ядерной физики. −
М.: Гос. изд-во
физ.-мат. лит-ры,
1961, с. 307.
t
t
33
34. ОСОБЕННОСТИ ИЗМЕРЕНИЯ МАЛЫХ ДЛИТЕЛЬНОСТЕЙ
При уменьшении длительностиизмеряемого интервала погрешность
квантования недопустимо возрастает;
от прямого счёта меток приходится
отказываться.
Можно «растянуть» интервал малой
длительности, например, заряжая
конденсатор в течение измеряемого
интервала, а затем разряжая его
во много раз меньшим током. Ещё проще
измерить напряжение на заряженном
конденсаторе с помощью АЦП.
34
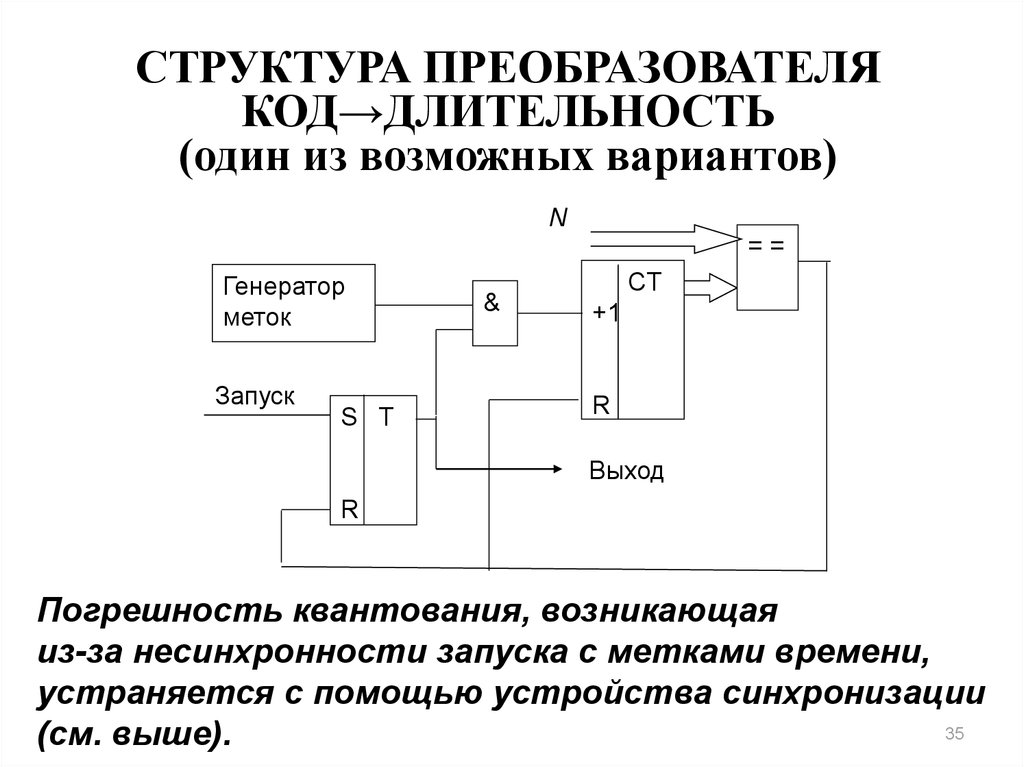
35. СТРУКТУРА ПРЕОБРАЗОВАТЕЛЯ КОД→ДЛИТЕЛЬНОСТЬ (один из возможных вариантов)
N==
Генератор
меток
Запуск
S T
&
CT
+1
R
Выход
R
Погрешность квантования, возникающая
из-за несинхронности запуска с метками времени,
устраняется с помощью устройства синхронизации
35
(см. выше).
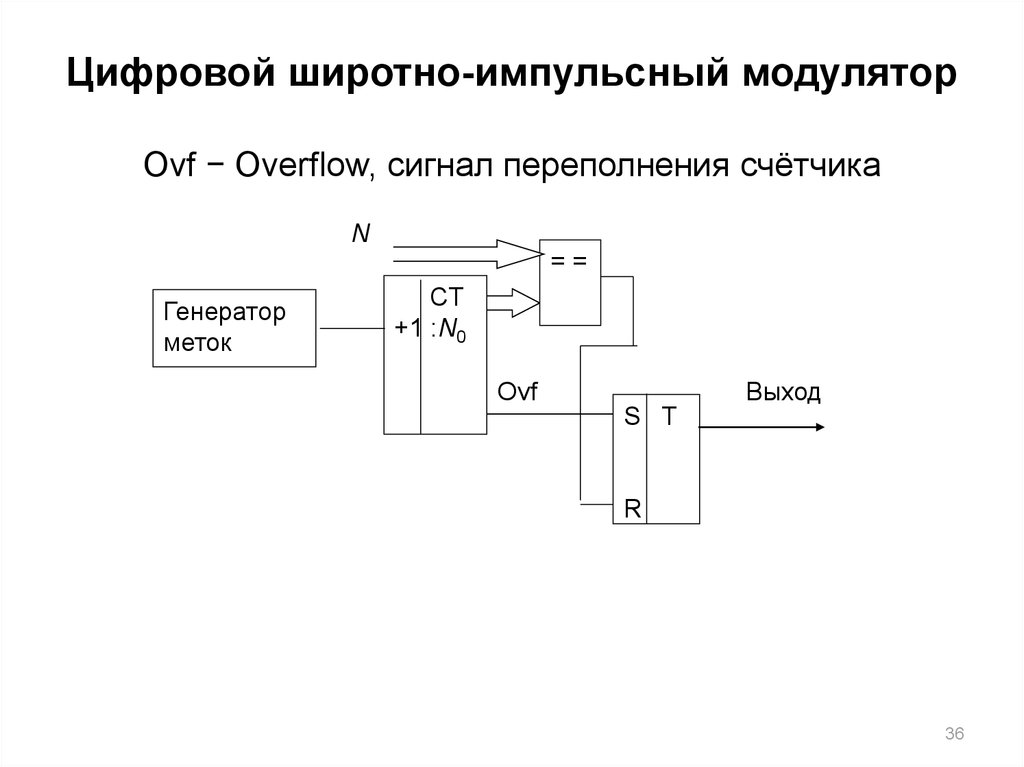
36. Цифровой широтно-импульсный модулятор Ovf − Overflow, сигнал переполнения счётчика
N==
Генератор
меток
CT
+1 :N0
Выход
Ovf
S T
R
36
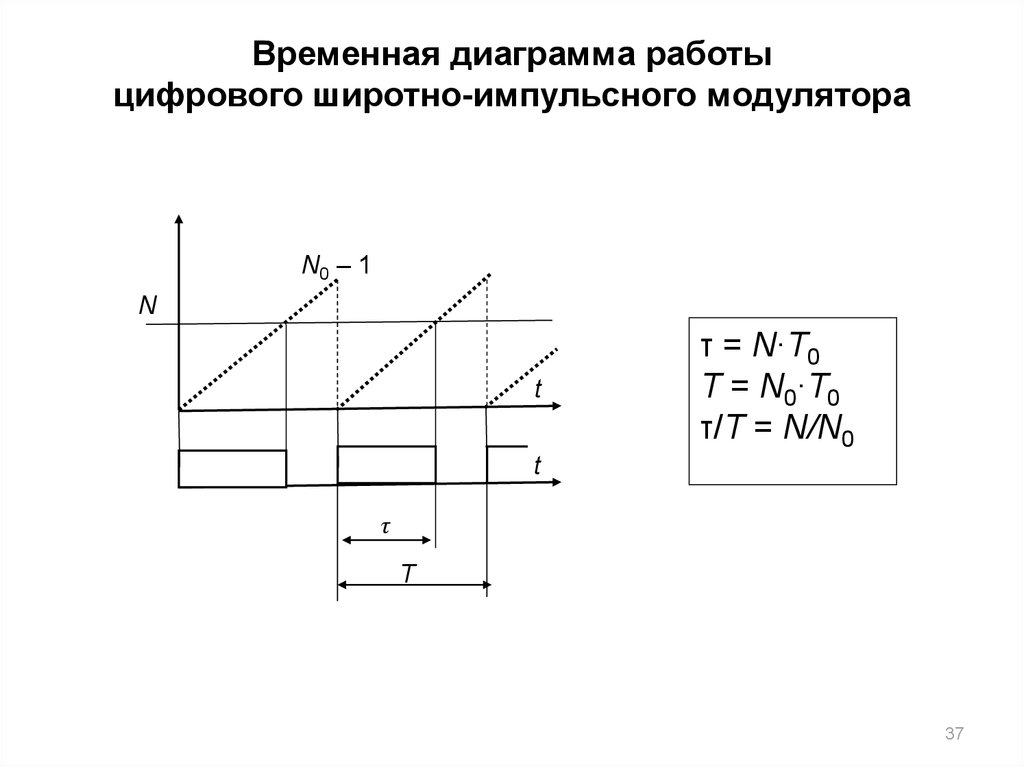
37. Временная диаграмма работы цифрового широтно-импульсного модулятора
N0 – 1N
t
τ = N∙T0
T = N0∙T0
τ/T = N/N0
t
τ
T
37
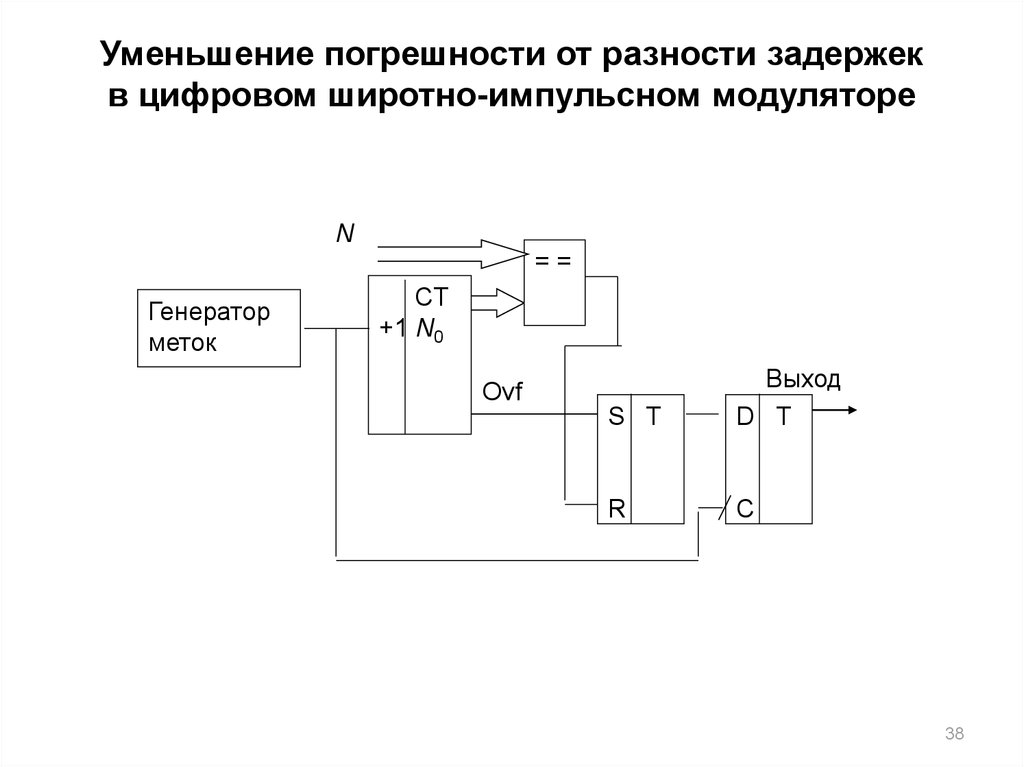
38. Уменьшение погрешности от разности задержек в цифровом широтно-импульсном модуляторе
N==
Генератор
меток
CT
+1 N0
S T
Выход
D T
R
C
Ovf
38
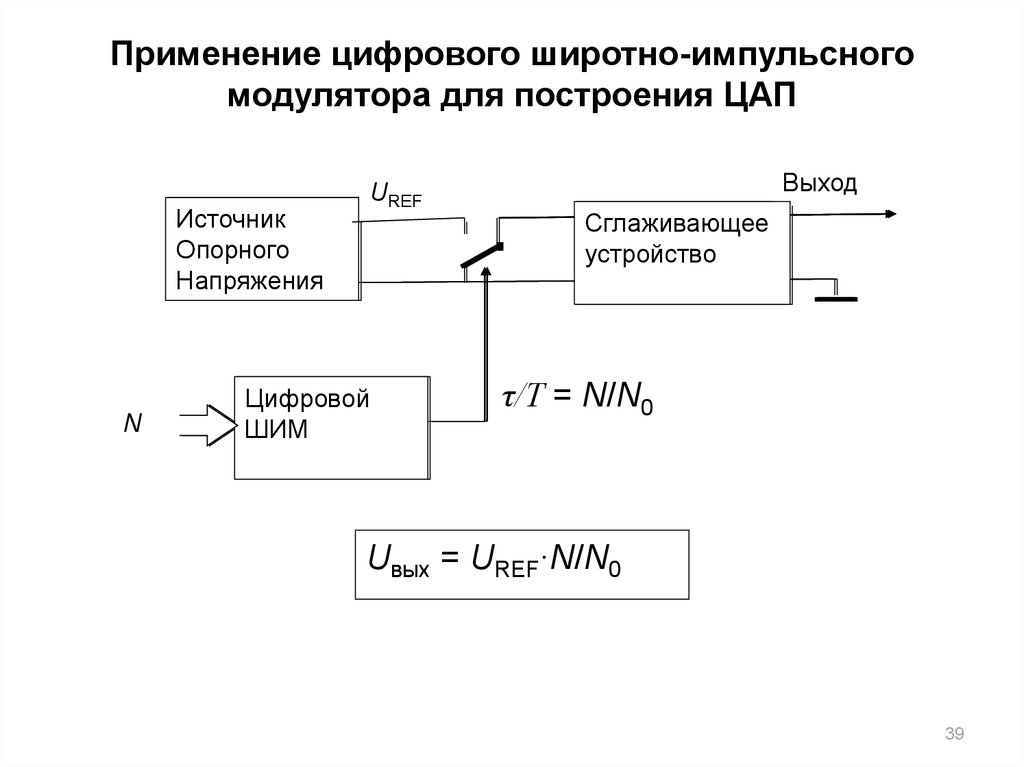
39. Применение цифрового широтно-импульсного модулятора для построения ЦАП
ИсточникОпорного
Напряжения
N
UREF
REF
Цифровой
ШИМ
Выход
Сглаживающее
устройство
τ/T = N/N0
Uвых = UREF∙N/N0
39
40. ПРИНЦИПЫ ПРЕОБРАЗОВАНИЯ ЧАСТОТА→КОД
• Прямой счёт циклов сигнала в течениезаданного измерительного интервала.
• Измерение «по периоду» (длительности
одного или нескольких циклов сигнала).
• Измерение по спектру.
40
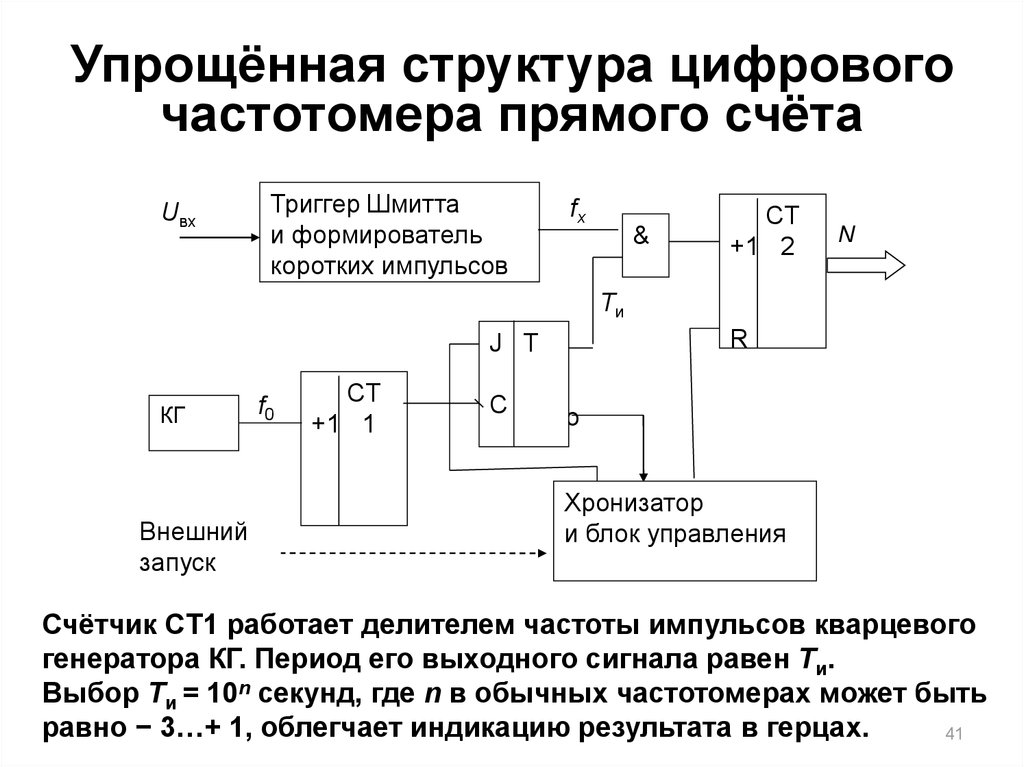
41. Упрощённая структура цифрового частотомера прямого счёта
UвхТриггер Шмитта
и формирователь
коротких импульсов
fx
&
CT
+1 2
N
Tи
R
J T
КГ
Внешний
запуск
f0
CT
+1 1
C
о
Хронизатор
и блок управления
Счётчик CT1 работает делителем частоты импульсов кварцевого
генератора КГ. Период его выходного сигнала равен Tи.
Выбор Tи = 10n секунд, где n в обычных частотомерах может быть
равно − 3…+ 1, облегчает индикацию результата в герцах.
41
42. Что измеряет цифровой частотомер прямого счёта?
Результат счёта есть оценка статистическойчастоты срабатываний триггера Шмитта на интервале Tи.
При случайном потоке событий погрешность
квантования заменяется статистическим разбросом
результатов (для пуассоновского потока σ = √N).
При гармоническом модулированном сигнале
результат счёта (с погрешностью квантования ±1 импульс)
совпадает со средней фазовой частотой на том же
интервале.
При периодическом сигнале простой формы он
(с той же погрешностью квантования ±1 импульс)
совпадает с хронометрической частотой.
42
43. Состав погрешностей цифрового частотомера прямого счёта
Погрешность серийных счётчиковых частотомеровв режиме прямого счёта нормировалась как
1
f ( 0
).
f xTи
Здесь δf − относительная погрешность
измерения частоты, δ0 − погрешность кварцевого
генератора (порядка 10−7); второй член
представляет погрешность квантования.
У нестандартных частотомеров на основе
микроконтроллеров погрешность кварца может
быть значительно больше. Могут проявиться
погрешности от задержек при формировании
строба, которые в серийных приборах сведены
к минимуму.
43
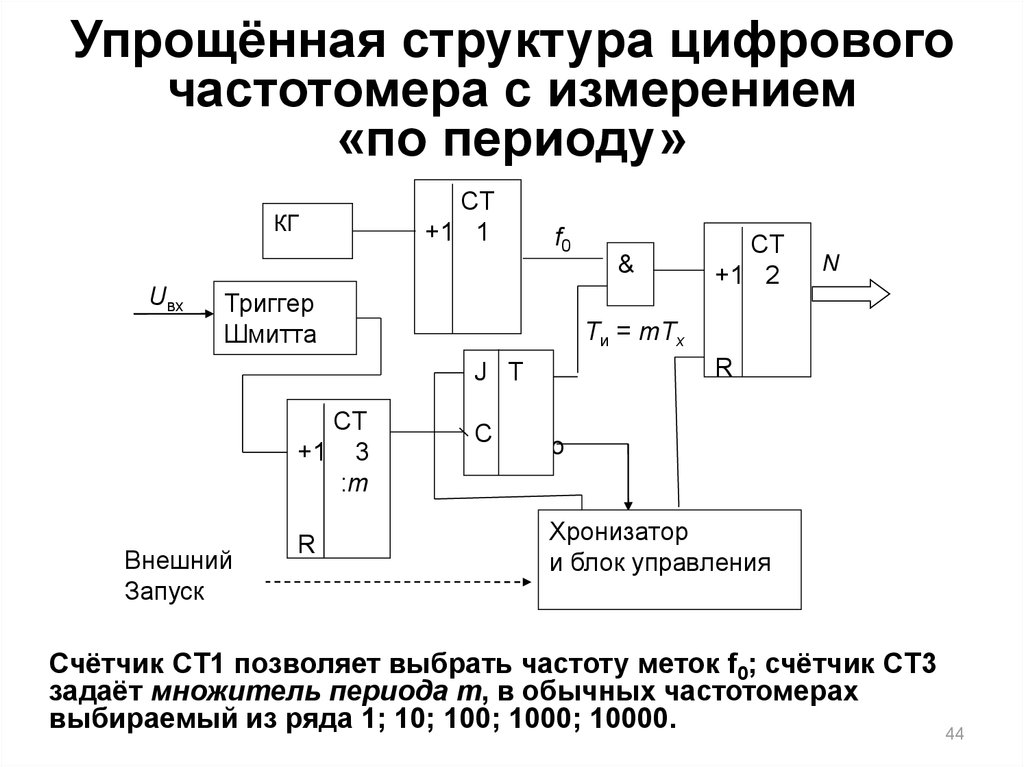
44. Упрощённая структура цифрового частотомера с измерением «по периоду»
КГUвх
CT
+1 1
f0
Триггер
Шмитта
Внешний
Запуск
R
N
Tи = mTx
R
J T
CT
+1 3
:m
&
CT
+1 2
C
о
Хронизатор
и блок управления
Счётчик CT1 позволяет выбрать частоту меток f0; счётчик CT3
задаёт множитель периода m, в обычных частотомерах
выбираемый из ряда 1; 10; 100; 1000; 10000.
44
45. Нахождение измеряемой частоты при измерении «по периоду»
По результату счёта N ≈ f0mTx частотавычисляется как fx = 1/Tx ≈ f0m/N. Для
удобства вычисления частоты «вручную»,
Tx индицируют в секундах, миллисекундах
или микросекундах. Это не требует
вычислений в приборе, если коэффициент
f0m равен (в герцах) степени десяти.
Применение в приборе микропроцессора
исключает вычисление частоты «вручную»,
но делает работу прибора «непрозрачной».
45
46. Состав погрешностей цифрового частотомера с измерением «по периоду»
Наряду с погрешностью меры(кварцевого генератора КГ)
и погрешностью квантования 1/(f0mTx),
существенна (иногда преобладает)
погрешность формирования строба mTx,
вызванная шумами на входе
формирователя − триггера Шмитта.
Этими шумами обусловлена
неопределённость выявления момента
перехода входного сигнала через
уровень компарирования.
46
47. Расчёт относительной погрешности формирования строба, вызванной шумом
Полагаем сигнал синусоидальным2
u U с sin
t;
Tx
шум − находящимся в пределах
±uш.
± uш
± Δt
При уровне компарирования, близком к нулю,
скорость изменения напряжения составит
du 2
Uс.
dt Tx
47
48.
Находим пределы отклонения моментакомпарирования от правильного положения
uш
uш Tx
t
.
du
U с 2
dt
Относим удвоенные (получающиеся в начале и
в конце строба) отклонения к стробу mTx:
uш
uш
2 t
ш
.
mTx mU с 3mU с
Расчёт очень грубый, но соответствует
обычной неточности данных о шуме.
48
49. Формирование строба путём компарирования становится затруднительным или невозможным при сильно зашумлённом или сложном сигнале
Некоторые способы уменьшения влиянияшума рассмотрены в книге:
Кирианаки Н. В., Гайдучок Р. М. Цифровые
измерения частотно-временных параметров
сигналов.−Львов: Вища школа. Изд-во при
Львовском ун-те, 1978. − 167 с.
Студент Пархоменко в выпускной работе
бакалавра находил период сложного
колебания (гитарной струны) программным
путём по массиву отсчётов сигнала,
полученному с помощью АЦП. Роль меток
времени играли сигналы запуска АЦП.
49
50. Метод зависимого счёта при измерении частоты «по периоду»
Недостатком измерения при заданноммножителе периода m является изменение
измерительного интервала mTx при изменении
измеряемой частоты. При зависимом счёте
назначается желаемый измерительный
интервал, и число m усредняемых циклов
сигнала увеличивается по ходу счёта, пока
конец интервала mTx не выйдет за границы
желаемого измерительного интервала. Теперь
число m зависит от Tx , его нужно каждый раз
находить с помощью счётчика, и вычисления
в приборе делаются предпочтительными.
50
51. Сравнение погрешностей при измерении частоты прямым счётом и «по периоду»
При измерении методом прямого счёта погрешностьна низких частотах определяется квантованием.
Например, при fx = 50 Гц и Tи = 10 с (разрешение 0,1 Гц)
получается N = 500 и δf = 0,2 %.
По мере повышения частоты относительная погрешность
квантования уменьшается, и при достижении N = 107
становится сравнимой с погрешностью кварца 0,00001 %.
При измерении «по периоду» погрешность
уменьшается по мере понижения частоты.
Например, пусть опять fx = 50 Гц, т. е. Tx = 20 мс.
Выбрав m = 100, чтобы измерительный интервал
составил 2 с, и f0 = 10 МГц (период меток 100 нс),
получаем N = 2∙107.
В этих условиях погрешность определяется шумом.
Положим uш = 10 мкВ; Uс = 3,3 В; тогда δш ≈ 0,01 %.
51
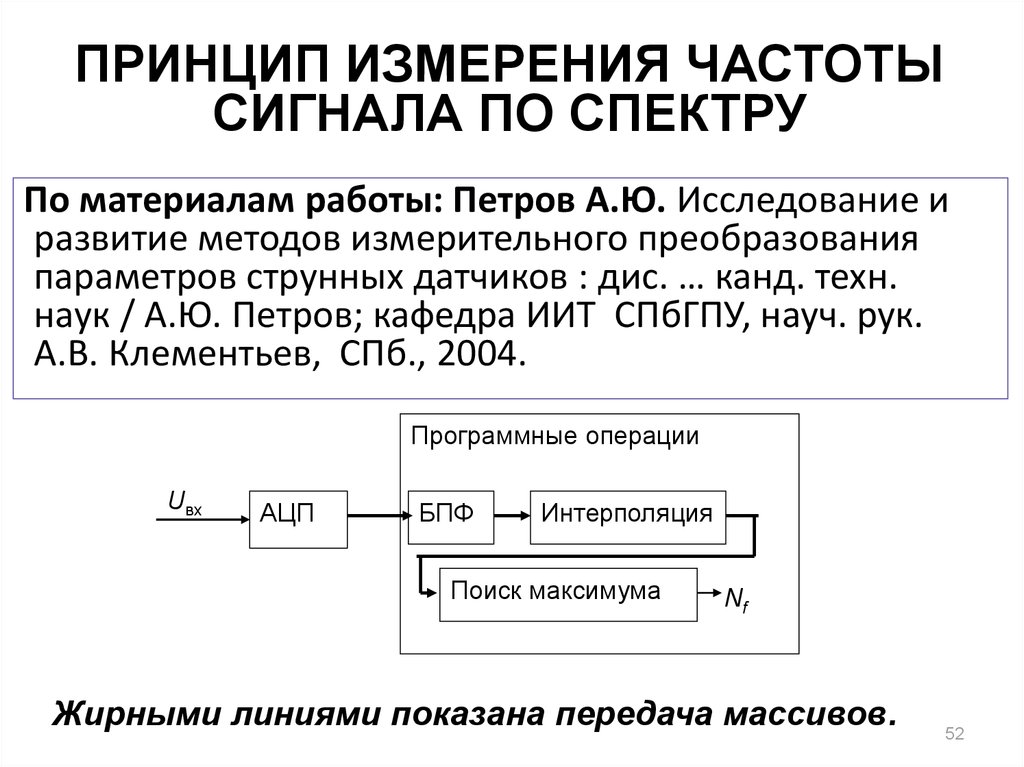
52. ПРИНЦИП ИЗМЕРЕНИЯ ЧАСТОТЫ СИГНАЛА ПО СПЕКТРУ
По материалам работы: Петров А.Ю. Исследование иразвитие методов измерительного преобразования
параметров струнных датчиков : дис. … канд. техн.
наук / А.Ю. Петров; кафедра ИИТ СПбГПУ, науч. рук.
А.В. Клементьев, СПб., 2004.
Программные операции
Uвх
АЦП
БПФ
Интерполяция
Поиск максимума
Nf
Жирными линиями показана передача массивов.
52
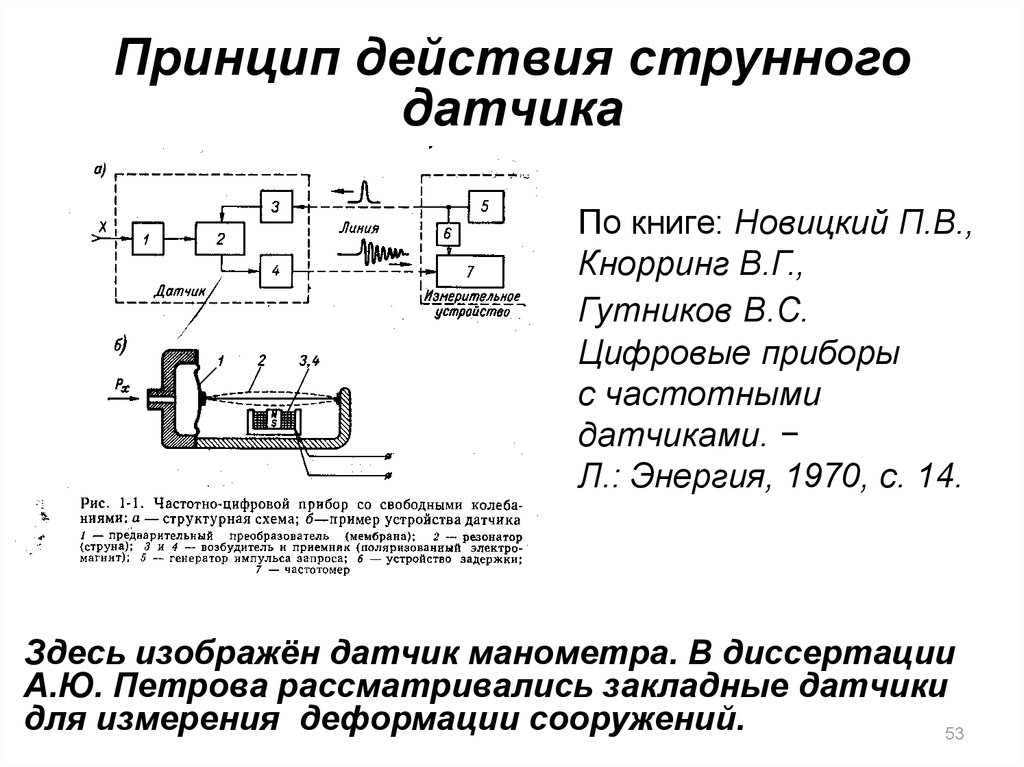
53. Принцип действия струнного датчика
По книге: Новицкий П.В.,Кнорринг В.Г.,
Гутников В.С.
Цифровые приборы
с частотными
датчиками. −
Л.: Энергия, 1970, с. 14.
Здесь изображён датчик манометра. В диссертации
А.Ю. Петрова рассматривались закладные датчики
для измерения деформации сооружений.
53
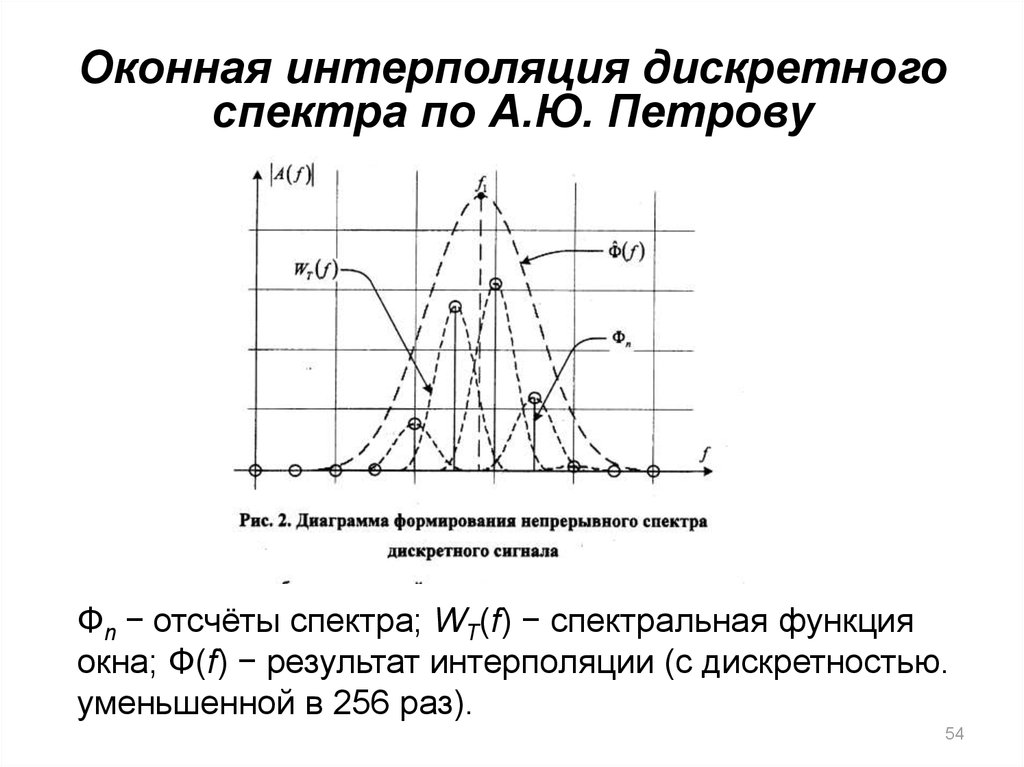
54. Оконная интерполяция дискретного спектра по А.Ю. Петрову
Φn − отсчёты спектра; WT(f) − спектральная функцияокна; Φ(f) − результат интерполяции (с дискретностью.
уменьшенной в 256 раз).
54
55. ПРИМЕНЕНИЯ ПРЕОБРАЗОВАТЕЛЕЙ ЧАСТОТА→КОД
• Режимы преобразования частота→коди «период»→код предусматриваются во всех цифровых
частотомерах общего назначения.
• Особой областью являются измерения частоты
в энергетике. Там нужно непрерывно следить за
малыми изменениями частоты в электрических сетях.
• Имеется много частотных датчиков, т. е. датчиков,
информативным параметром выходного сигнала
которых является частота синусоидальных колебаний
или импульсов.
• В экспериментальной физике и в задачах
экологического мониторинга, связанных с
радиоактивностью, необходимо измерять интенсивность
потоков случайных событий, т. е. статистическую
частоту.
55
56. ЧАСТОТНЫЕ ДАТЧИКИ И ПРЕОБРАЗОВАТЕЛИ НАПРЯЖЕНИЕ→ЧАСТОТА
Отдельные виды частотных датчиков известны давно.Струнный метод измерения деформаций предложен
в Ленинградском политехническом институте
Н.Н. Давиденковым в начале 1930-х годов, а даты
изобретения частотных анемометров, тахометров
и расходомеров вообще вряд ли можно установить.
В 1959 г. Пётр Васильевич Новицкий на кафедре ИИТ
ЛПИ организовал систематическое исследование
частотных датчиков с колебательными системами
различной природы. Результаты первого десятилетия
этой работы отражены в монографии: Новицкий П.В.,
Кнорринг В.Г., Гутников В.С. Цифровые приборы с
частотными датчиками. − Л.: Энергия, 1970. − 424 с.
Позже приобрели актуальность преобразователи
напряжение→частота с линейными характеристиками
преобразования. В настоящее время они выпускаются
в виде микросхем.
56
57. МИКРОСХЕМЫ ПРЕОБРАЗОВАТЕЛЕЙ НАПРЯЖЕНИЕ→ЧАСТОТА (ПНЧ)
Основу современного ПНЧ образует интегратор.Скорость изменения его выходного напряжения
пропорциональна входному напряжению.
• В ПНЧ без сигнальной обратной связи выходное
напряжение интегратора колеблется с заданной
амплитудой: при достижении им заданного уровня
срабатывает компаратор и либо разряжает
интегратор, либо переключает направление
интегрирования. Второе предпочтительнее.
• В ПНЧ с сигнальной обратной связью заряд
интегратора, создаваемый входным сигналом,
уравновешивается зарядом от импульсов обратной
связи. Момент формирования импульса обратной
связи определяется компаратором.
Во всех вариантах частота срабатываний компаратора
получается пропорциональной входному напряжению. 57
58. ПРИМЕР МИКРОСХЕМЫ ПНЧ БЕЗ СИГНАЛЬНОЙ ОБРАТНОЙ СВЯЗИ − AD654
AD654 − ПНЧ с изменением направления интегрирования.58
59.
Основная схема включения AD654для положительного входного напряжения
59
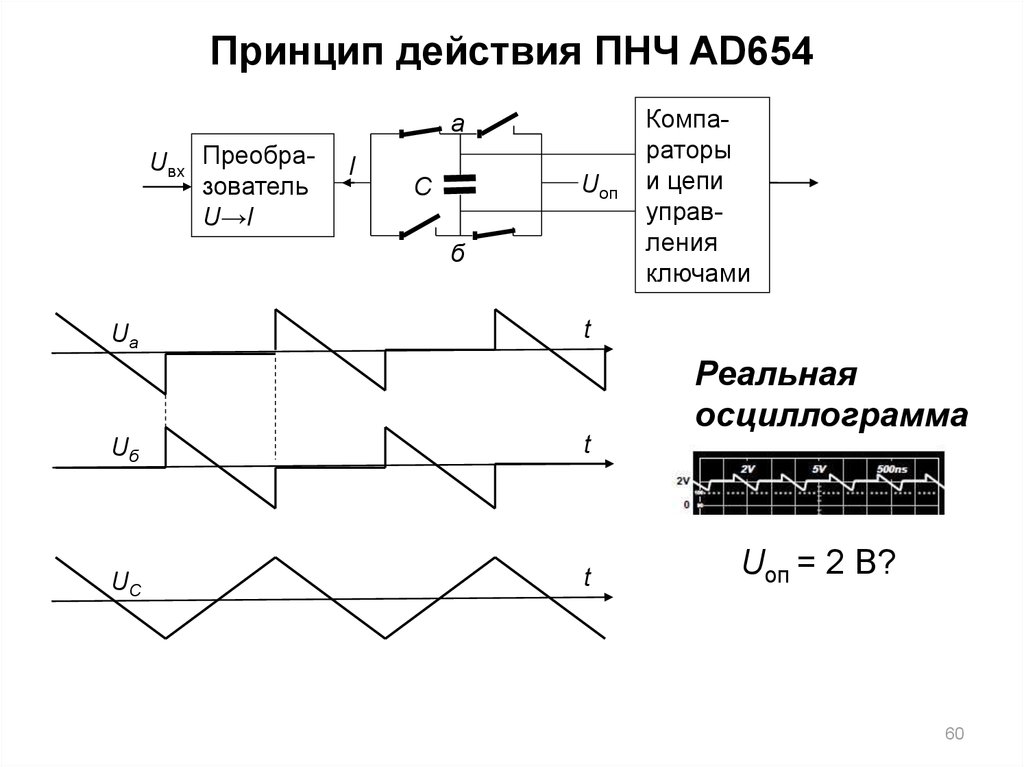
60. Принцип действия ПНЧ AD654
аUвх Преобразователь
U→I
I
Uоп
C
б
Uа
Компараторы
и цепи
управления
ключами
t
Реальная
осциллограмма
Uб
t
UC
t
Uоп = 2 В?
60
61. ПНЧ С СИГНАЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ РАЗЛИЧАЮТСЯ ПО СПОСОБАМ ФОРМИРОВАНИЯ ИМПУЛЬСА ОБРАТНОЙ СВЯЗИ
• Импульс с непосредственно заданным зарядомполучается путём разряда конденсатора,
заряженного до опорного напряжения.
• Импульс с непосредственно заданной
вольтсекундной площадью получается путём
перемагничивания сердечника с прямоугольной
петлёй гистерезиса.
• В прямоугольном импульсе тока (или напряжения)
раздельно задаются амплитуда тока (или
напряжения) и длительность импульса.
Длительность прямоугольного импульса может
задаваться, например, одновибратором
(в «асинхронных» ПНЧ) или тактовым генератором
(в «синхронных» ПНЧ).
61
62. ПРИМЕР МИКРОСХЕМЫ «АСИНХРОННОГО» ПНЧ/ПЧН С ТОКОВЫМ ПРЯМОУГОЛЬНЫМ ИМПУЛЬСОМ ОБРАТНОЙ СВЯЗИ − КР1108ПП1 (VFC32, ADVFC32)
Подробное описаниеулучшенного
ПНЧ/ПЧН КР1108ПП1
Рижского объединения
«Альфа» (СССР) − см.
Гутников 1988,
с. 269−273.
62
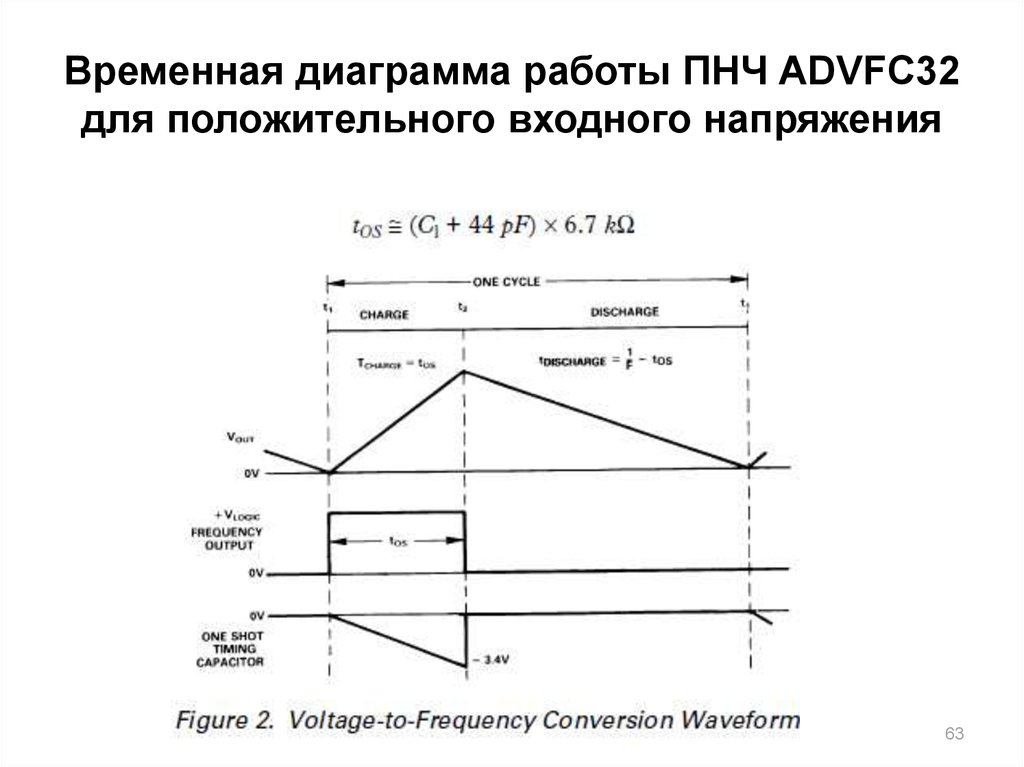
63. Временная диаграмма работы ПНЧ ADVFC32 для положительного входного напряжения
6364. Выходная частота ПНЧ ADVFC32
Разработчики микросхемы приняли остроумное решение:в ней два одинаковых стабилизатора тока.
Один ток образует импульсы обратной связи (а в паузах «помогает»
операционному усилителю), другой заряжает ёмкость одновибратора.
В формулу для частоты входит их отношение, поэтому одинаковое
изменение двух токов не влияет на частоту:
f в ых
U вх I2
1
.
U REF I1 RинтСов
В формулу входят также отношение входного напряжения
к модулю напряжения внутреннего опорного источника UREF
(до этого напряжения заряжается ёмкость одновибратора)
и произведение параметров навесных элементов: резистора
интегратора Rинт и конденсатора одновибратора Cов.
64
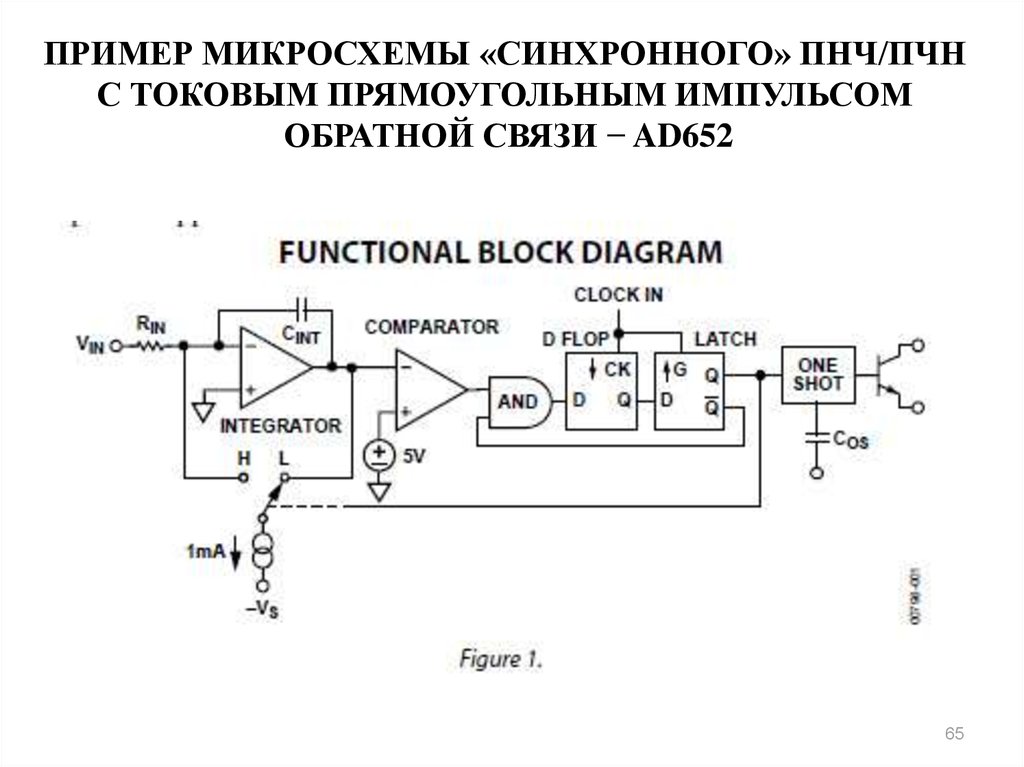
65. ПРИМЕР МИКРОСХЕМЫ «СИНХРОННОГО» ПНЧ/ПЧН С ТОКОВЫМ ПРЯМОУГОЛЬНЫМ ИМПУЛЬСОМ ОБРАТНОЙ СВЯЗИ − AD652
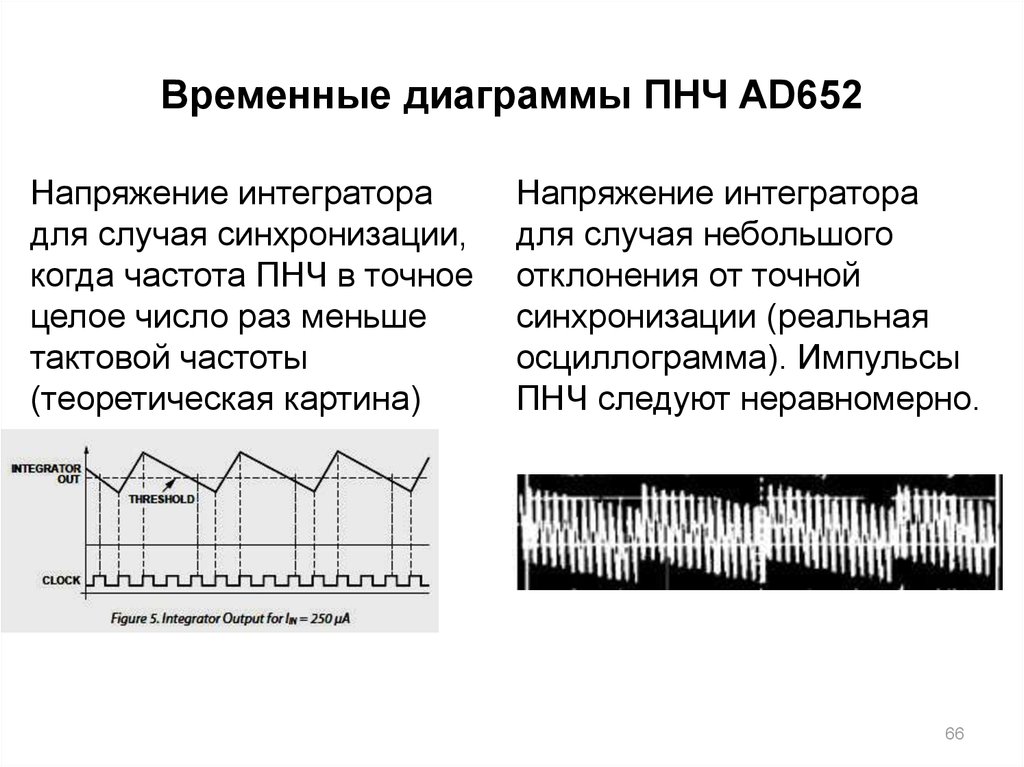
6566. Временные диаграммы ПНЧ AD652
Напряжение интеграторадля случая синхронизации,
когда частота ПНЧ в точное
целое число раз меньше
тактовой частоты
(теоретическая картина)
Напряжение интегратора
для случая небольшого
отклонения от точной
синхронизации (реальная
осциллограмма). Импульсы
ПНЧ следуют неравномерно.
66
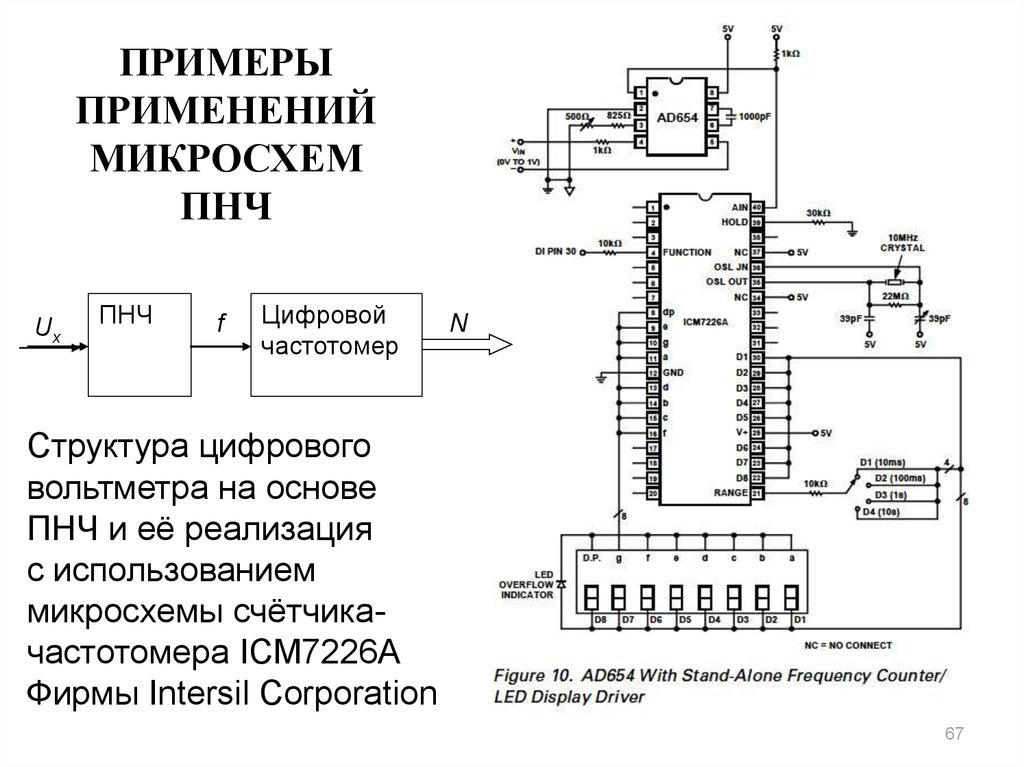
67. ПРИМЕРЫ ПРИМЕНЕНИЙ МИКРОСХЕМ ПНЧ
UxПНЧ
f
Цифровой
частотомер
N
Структура цифрового
вольтметра на основе
ПНЧ и её реализация
с использованием
микросхемы счётчикачастотомера ICM7226A
Фирмы Intersil Corporation
67
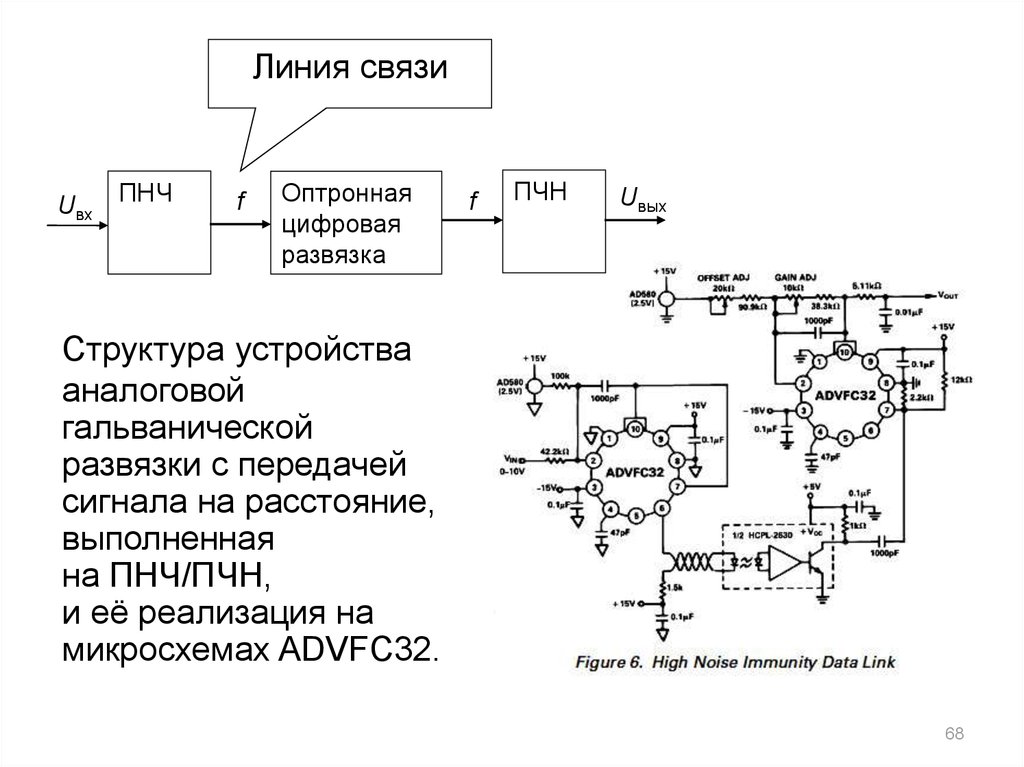
68.
Линия связиUвх ПНЧ
f
Оптронная
цифровая
развязка
f
ПЧН
Uвых
Структура устройства
аналоговой
гальванической
развязки с передачей
сигнала на расстояние,
выполненная
на ПНЧ/ПЧН,
и её реализация на
микросхемах ADVFC32.
68
69. ПРИНЦИПЫ ПРЕОБРАЗОВАНИЯ КОД → ЧАСТОТА
• Объединение импульсных потоковс частотами, взвешенными по двоичному
закону («двоичный умножитель»)
• Использование петли ФАПЧ в сочетании с
кодоуправляемым делителем частоты
• Прямой цифровой синтез
69
70. BINARY RATE MULTIPLIER («двоичный умножитель»)
f0t
f0/2
t
f0/4
t
f0/8
t
f0/2 + f0/8
t
f0
f ср n
2
n
2
i 1
i
i 1
N
f0 n
2
Возможная
реализация −
Гутников 1988,
с. 180−182
70
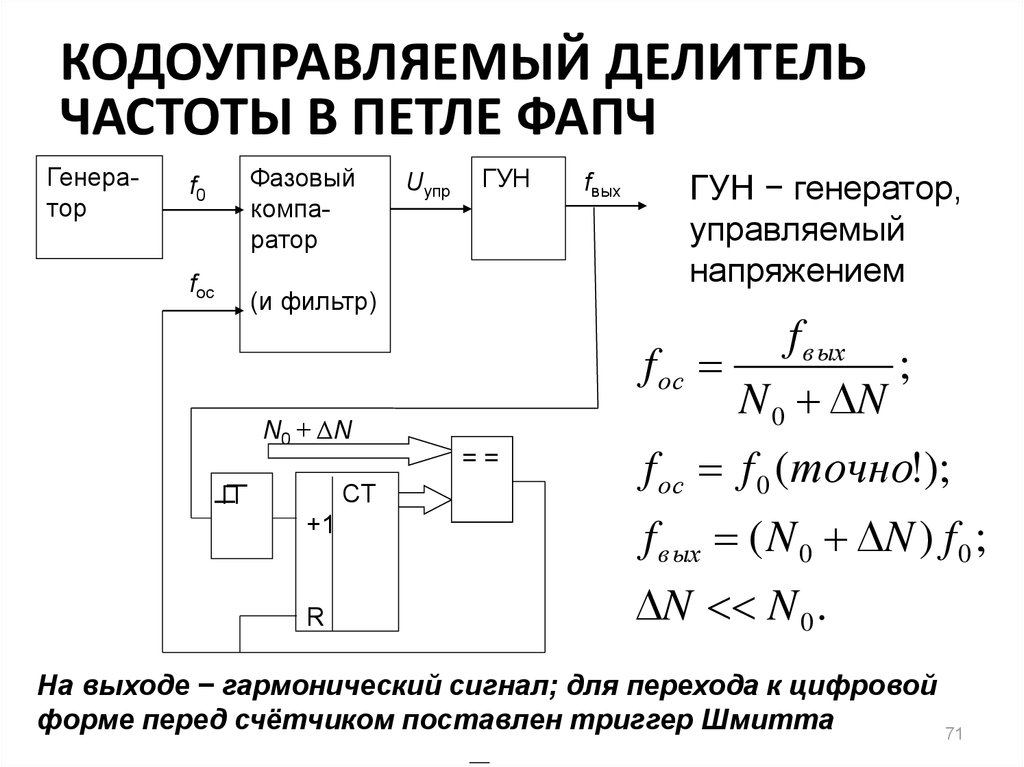
71. КОДОУПРАВЛЯЕМЫЙ ДЕЛИТЕЛЬ ЧАСТОТЫ В ПЕТЛЕ ФАПЧ
ГенераторФазовый
компаратор
f0
fос
Uупр
ГУН
(и фильтр)
==
CT
+1
R
ГУН − генератор,
управляемый
напряжением
f в ых
f ос
;
N 0 N
N0 + ΔN
П
fвых
f ос f 0 (точно!);
f в ых ( N 0 N ) f 0 ;
N N 0 .
На выходе − гармонический сигнал; для перехода к цифровой
форме перед счётчиком поставлен триггер Шмитта
71
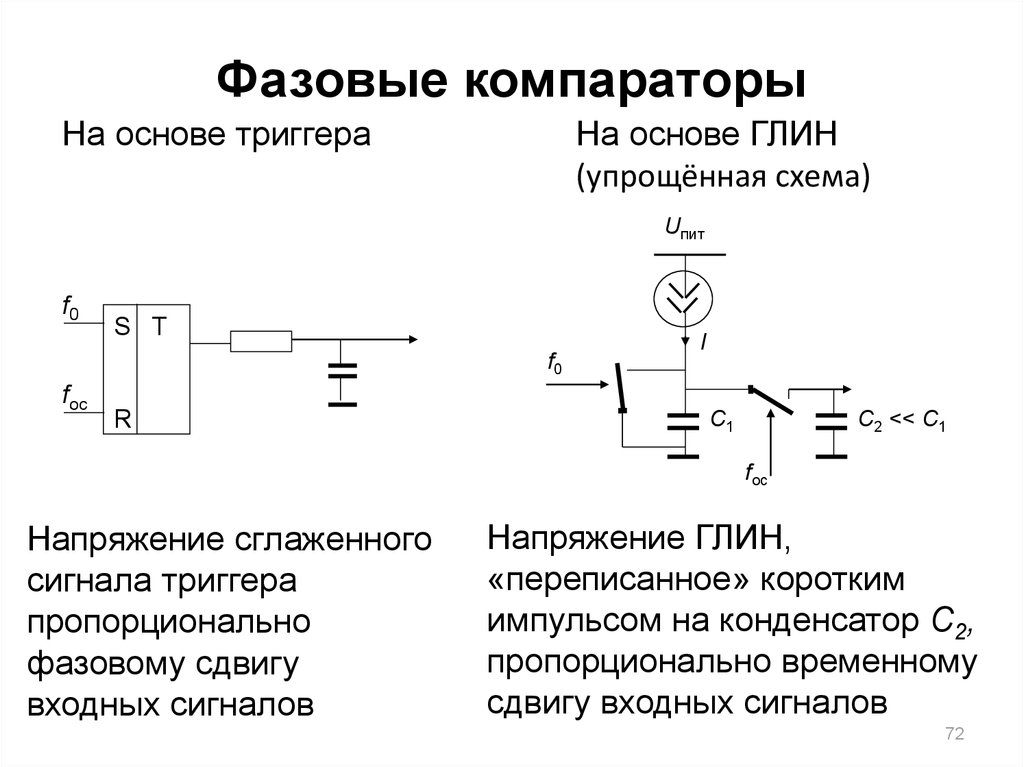
72. Фазовые компараторы
На основе триггераНа основе ГЛИН
(упрощённая схема)
Uпит
f0
S T
f0
fос
R
I
C1
C2 << C1
fос
Напряжение сглаженного
сигнала триггера
пропорционально
фазовому сдвигу
входных сигналов
Напряжение ГЛИН,
«переписанное» коротким
импульсом на конденсатор C2,
пропорционально временному
сдвигу входных сигналов
72
73. ПРЯМОЙ ЦИФРОВОЙ СИНТЕЗ ГАРМОНИЧЕСКОГО СИГНАЛА (Direct Digital Synthesis − DDS)
Пример − микросхема AD9831 с параллельным16-битовым интерфейсом
73
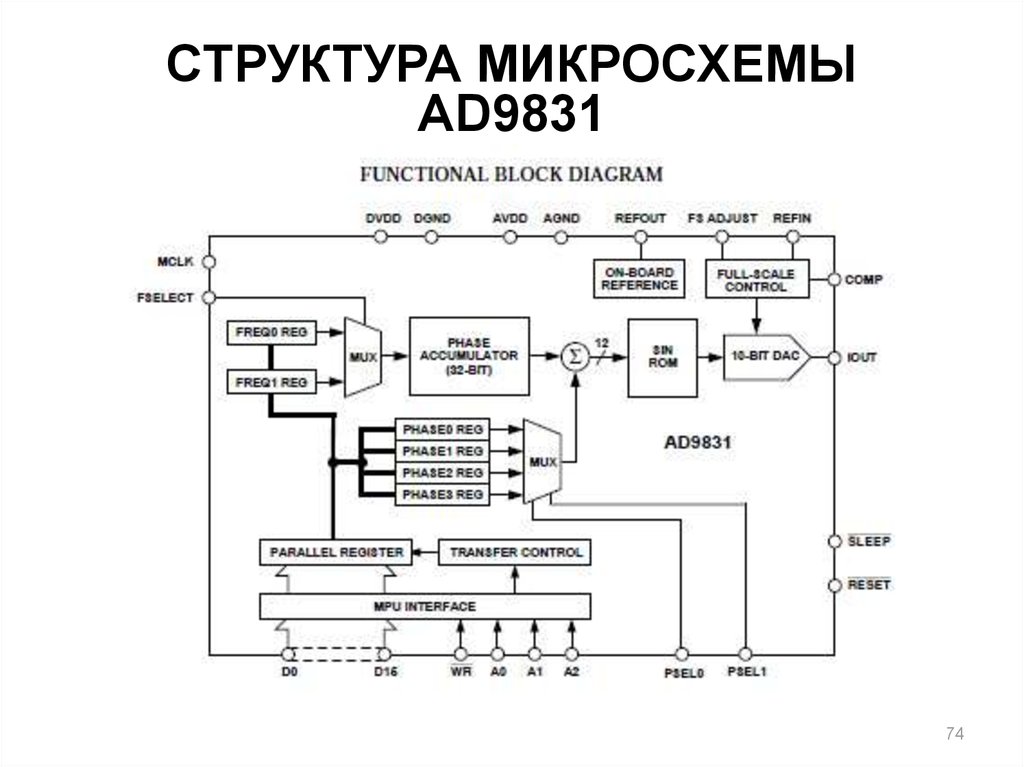
74. СТРУКТУРА МИКРОСХЕМЫ AD9831
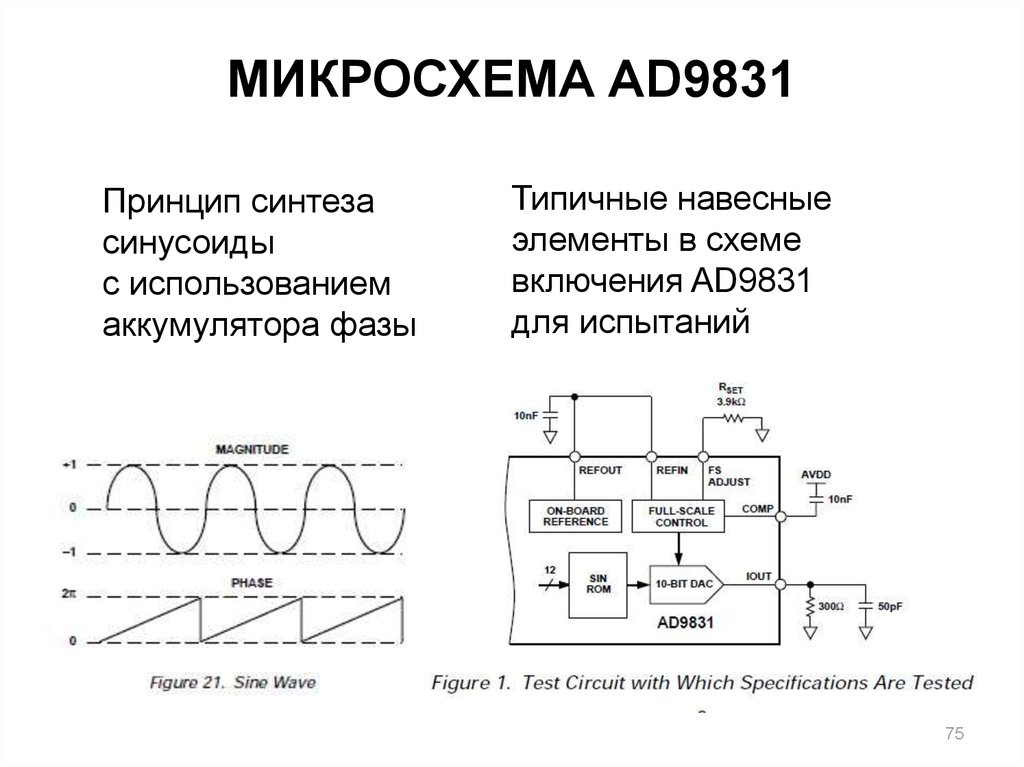
7475. МИКРОСХЕМА AD9831
Принцип синтезасинусоиды
с использованием
аккумулятора фазы
Типичные навесные
элементы в схеме
включения AD9831
для испытаний
75
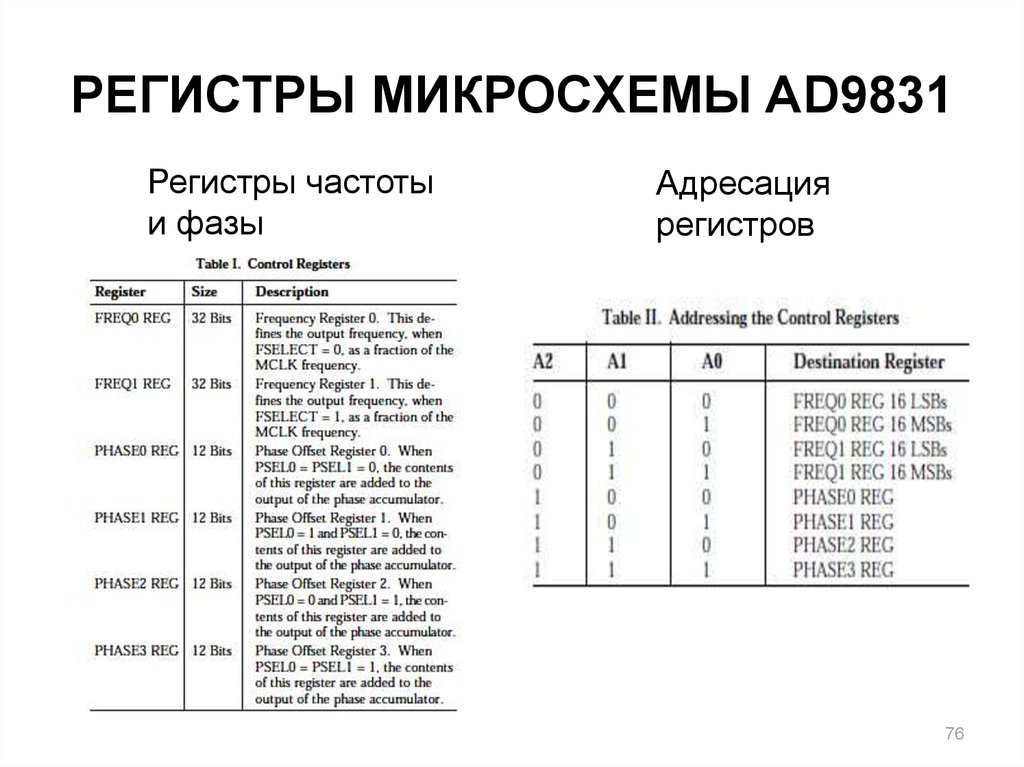
76. РЕГИСТРЫ МИКРОСХЕМЫ AD9831
Регистры частотыи фазы
Адресация
регистров
76
77. СРАВНЕНИЕ ПРИНЦИПОВ ПРЕОБРАЗОВАНИЯ КОД → ЧАСТОТА
• Двоичный умножитель имеет на выходепоследовательность импульсов, в
общем случае неравномерную.
Неравномерность можно сгладить (не
до конца) делителем частоты. Такой
сигнал годится, например, для
управления шаговым двигателем, но не
для решения задач, требующих чистоты
спектра сигнала.
77
78.
• Петля ФАПЧ с кодоуправляемымделителем частоты обеспечивает на
выходе гармонический сигнал с чистым
спектром, который может иметь
высокую частоту. Её недостаток − узкий
относительный диапазон изменения
выходной частоты (по условию
устойчивости). В синтезаторе частоты
Г3-110 диапазон 0,01 − 1999999,99 Гц
достигается использованием шести
петель ФАПЧ и промежуточных
преобразователей частоты.
78
79.
• Прямой цифровой синтез обеспечиваетформирование сигнала с чистым
спектром в широком относительном
диапазоне частот, например, у
микросхемы AD9831 при тактовой
частоте 25 МГц −
от 25∙106/232 ≈ 0,00582 Гц до 8 МГц
(почти ⅓ тактовой частоты!). Его
недостаток − ограничение абсолютного
диапазона выходных частот сверху.
79
80.
• Сравнивая ФАПЧ и прямой цифровойсинтез как методы, обеспечивающие
спектрально чистые сигналы, видим:
ФАПЧ может формировать сигналы
намного более высоких частот для
задач радиотехники; зато прямой
цифровой синтез позволяет мгновенно
переключать частоту или фазу сигнала,
что полезно для частотной или фазовой
манипуляции (FSK. PSK). Прямой
цифровой синтез реализован в одной
микросхеме (не считая задающего
генератора), с ФАПЧ это не так.
80
81.
Частотно-цифровая техника нашласвоеобразное продолжение в виде
ΣΔ (сигма-дельта) модуляции, которая
стала популярнейшим принципом
аналого-цифрового преобразования.
81















































 electronics
electronics








